Unidad No. II. Costo de capital y estructura de capital.

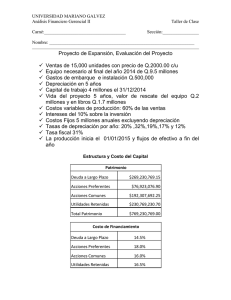
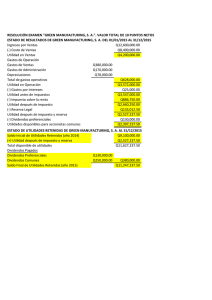
Ra
Asignatura
Carrera
Año Académico
Unidad No. II
Profesor
:
:
:
:
:
Finanzas II.
Ingeniería en sistemas.
III Año
Costo de capital y estructura de capital
MSc. Mauricio Navarro Zeledón.
Unidad II: Costo de capital y estructura de capital.
1. Descripción general del costo de capital.
El costo de capital es un concepto financiero de suma importancia, pues constituye un vínculo
esencial entre las decisiones de inversión a largo plazo de la empresa y la inversión de los
propietarios, según lo determinan los inversionistas en el mercado. Se trata, en efecto del “número
mágico” empleado para decidir si una inversión corporativa propuesta producirá un aumento o
disminución en el valor accionario de la empresa. Por supuesto que sólo resultarían recomendables
aquellas inversiones de las que se espera un incremento en el precio por acción [VPN (al costo de
capital) > 0, o TIR > el costo de capital]
El costo de capital puede definirse como la tasa de rendimiento que debe ser percibida por una
empresa sobre su inversión proyectada, con el objeto de mantener inalterado el valor de mercado de
sus acciones. Asimismo, se considera como la tasa de rendimiento requerida por los proveedores
del mercado de capitales para atraer sus fondos hacia la empresa. Si se mantiene el riesgo
constante, la aplicación de proyectos con una tasa de rendimiento por encima del costo de capital,
se incrementará el valor de la empresa y viceversa.
Supuestos básicos.
El costo de capital es un concepto dinámico afectado por una diversidad de factores económicos y
empresariales. Con el fin de aislar la estructura básica del costo de capital, se realizan algunos
supuestos básicos con respecto al riesgo y los impuestos.
a. Riesgo empresarial –el riesgo de que la empresa no sea capaz de cubrir sus costos de
operación- se supone inalterado. Este supuesto implica que la aceptación de un proyecto
determinado por parte de la empresa, deja inalterada la capacidad de la misma para cubrir los
costos de operación.
b. Riesgo financiero –el riesgo de que la empresa no sea capaz de cumplir con sus obligaciones
financieras requeridas (intereses, pagos de arrendamientos, dividendos de acciones
preferentes)- se supone inalterado. Este supuesto implica que los proyectos son financiados de
forma tal, que la capacidad de la empresa para cumplir con sus costos de financiamiento
requeridos queda inalterada.
c. Los costos después de impuestos se consideran relevantes. Es decir, el costo de capital se mide
sobre una base después de impuestos. Observe que este supuesto es congruente con el
método empleado en la toma de decisiones del presupuesto de capital.
El costo de capital se estima en una fecha determinada. Refleja el promedio esperado del costo
futuro de los fondos a largo plazo, con base en la mejor información disponible. Esta noción es
compatible con el uso del costo de capital para la toma de decisiones de inversión financiera a largo
plazo
2. Costo de la deuda a largo plazo.
El costo de la deuda a largo plazo (bonos), ki es el costo presente después de impuestos de la
obtención de fondos a largo plazo mediante préstamos. Por comodidad, se supone aquí que los
fondos se obtienen a través de la emisión y venta de bonos. Además, se supone que los bonos
pagan intereses anuales en vez de semestrales.
Valores netos de realización.
La mayoría de los pasivos a largo plazo de las corporaciones se deben a la venta de bonos. Los
valores netos de realización de la venta de un bono, o de cualquier valor, son los fondos recibidos
realmente por dicha venta. Los costos de emisión –el costo total de emisión y venta de un valor –
reducen los valores netos de realización de un bono, sea éste vendido con prima, con descuento o
en su valor nominal.
Ejemplo.
Aceros S.A. importante fabricante de productos ferreteros, planea la venta de bonos por $ 10
millones, a 20 años y a 9% (tasa establecida de interés anual), cada bono tiene un valor nominal de
$ 1,000. Puesto que los bonos de riesgo similar perciben rendimientos mayores que la tasa de 9% la
empresa debe vender los bonos en $ 980, a fin de compensar por menor la tasa establecida de
interés. Los costos de emisión pagados, al banquero de inversiones son 2% del valor nominal del
bono (2% x $ 1,000), es decir, de $ 20. Los valores netos de realización para la empresa
procedentes de cada bono son, en consecuencia, de $ 960 ($ 980 - $ 20).
Costo de la deuda antes de impuestos.
El costo de la deuda antes de impuestos, kd, de un bono, puede obtenerse mediante uno de tres
métodos: cotización, cálculo o aproximación.
Cotizaciones de costos.
Cuando los valores netos de realización de un bono equivalen a su valor nominal, el costo antes de
impuestos será igual a la tasa establecida de interés. Por ejemplo, un bono con una tasa establecida
de interés del 10%, con valores netos de realización iguales a $ 1,000 del valor nominal del bono,
tendría un costo antes de impuestos, kd de 10%.
Cálculo del costo.
Esta técnica encuentra el costo antes de impuestos de la deuda mediante el cálculo de la TIR sobre
los flujos de efectivo del bono. Desde el punto de vista del emisor, se puede referir este valor como
el costo al vencimiento de los flujos de efectivo relacionados con la deuda. El costo al vencimiento
puede obtenerse con una calculadora financiera, una computadora o mediante las técnicas de tanteo
(ensayo error). Este costo representa el costo porcentual anual antes de impuestos de la deuda de la
empresa.
Ejemplo.
En el ejemplo anterior se encontró que los valores netos de realización de un bono de $ 1,000 a 20
años, con una tasa establecida de interés de 9% eran de $ 960. Si bien los flujos de efectivo de la
emisión de bonos no sigue un patrón convencional, el cálculo del costo anual resulta bastante
sencillo. En realidad, el patrón de flujos de efectivo es exactamente contrario al de un patrón
convencional, en cuanto a que éste consiste en una entrada inicial (valores netos de realización),
seguida por una serie de desembolsos anuales (los pagos de intereses). En el último año, cuando se
paga la deuda, también tiene lugar un desembolso que representa al reembolso del principal. Los
flujos de efectivo relacionados con la emisión de Aceros S.A. son los siguientes:
Fin de año
0
1 – 20
20
Flujo de efectivo
$ 960
( $ 90 )
( $ 1,000)
La entrada inicial de $ 960 va seguida por salidas de interés anual de $ 90 (9% de tasa establecida
de interés x valor nominal de $ 1,000) respecto a la vida de 20 años del bono. En el año 20 tiene
lugar un desembolso de $ 1,000, representando el desembolso del principal. El costo antes de
impuestos de la deuda puede determinarse encontrando la TIR, la tasa de descuento que iguala el
valor presente de las salidas de efectivo con la entrada inicial.
Tanteo (ensayo error). Como se sabe, el descuento de los flujos de efectivo futuro de un bono a su
tasa establecida de interés resultará en su valor nominal de $ 1,000, la tasa de descuento requerida
para hacer que el valor de los bonos de Aceros S.A. sea igual a $ 960 debe ser mayor que la tasa
establecida de interés de 9%. (Recuérdese que cuanto mayor sea la tasa de descuento, menor será
el valor presente y viceversa). Mediante el uso de computadora el costo antes de impuestos (costo al
vencimiento) es 9.452%.
Aproximación del costo.
El costo de la deuda antes de impuestos, kd, de un bono con valor nominal de $ 1,000 puede
obtenerse de manera aproximada mediante la ecuación:
Donde.
I = interés anual pagado (unidades monetarias)
Nd = valores netos de realización de la venta de la deuda (bonos).
n = número de años para el vencimiento del bono.
Ejemplo. Al sustituir los valores correspondiente del ejemplo de Aceros S.A. en la anterior ecuación
se obtiene:
3. Costo de las acciones preferentes.
Las acciones preferentes representan un tipo especial de interés sobre la propiedad de la empresa.
Los accionistas preferentes deben recibir sus dividendos establecidos antes de la distribución de
cualesquiera utilidades a los accinistas comunes. Como las acciones preferentes constituyen una
forma de propiedad, se espera que los ingresos provenientes de su venta sean mantenidos durante
un período infinito.
Dividendos de las acciones preferentes.
La mayor parte de los dividendos de las acciones preferentes son establecidos como un monto en
unidades monetarias: “x unidades monetarias por año”. Cuando los dividendos se presentan de esta
manera, es frecuente referirse a las acciones como a acciones preferentes de “x unidades
monetarias”. En consecuencia, se espera que “una acción preferente de $ 4 debe pagar a los
accionistas preferentes dividendos de $ 4 anuales. Algunas ocasiones los dividendos de las
acciones preferentes se establecen como una tasa porcentual anual. Dicha tasa representa un
porcentaje del valor nominal de la acción, valor equivalente al dividendo anual. Por ejemplo, de una
acción preferente a 8%, con un valor nominal de $ 50, se esperaría que pagase dividendos anuales
de $ 4 por acción (0.08 x $ 50 valor nominal = $ 4). Antes de calcular el costo de las acciones
preferentes, deben convertirse cualesquiera dividendos establecidos como porcentajes a dividendos
anuales en unidades monetarias)
Cálculo del costo de las accciones preferentes.
El costo de las acciones preferentes, kp, se calcula al dividir los dividendos anuales de ete tipo de
acciones, Dp, entre los valores netos de realización procedentes de su venta, Np. Los valores netos
de realización representan la cantidad de dinero recibida por concepto de los costos de emisión
requeridos para emitir y vender las acciones. En la siguiente ecuación se expresa el costo de las
acciones preferentes, kp, en términos del dividendo anual monetario, Dp, y de los valores netos de
realización procedentes de la venta de las acciones, Np.
Ejemplo.
Aceros S.A. planea la emisión de un paquete de acciones preferentes a 10% (dividendo anual), de
las cuales se espera vender en su valor nominal de $ 87 por acción. Se espera que el costo de
emisión y venta de las acciones sea de $ 5 por unidad. La empresa desearía determinar el costo de
paquete accionario. El primer paso consiste en calcular la cantidad en dólares de los dividendos
preferentes, puesto que tales dividendos se establecen como un porcentaje del valor nominal de las
acciones de $ 87. El dividendo anual es de $ 8.70 (0.10 x $ 87). Los valores netos de realización
provenientes de la venta propuesta se calculan al sustraer los costos de emisión al precio de la
venta, con lo que se obtiene un valor de acción por acción de $ 82. Al sustituir el dividendo anual,
Dp, de $ 8.70, y los valores netos de realización, Np, de $ 82, en la ecuación anterior se obtiene el
costo de las acciones preferentes, de 10.6% ($ 8.70 / $ 82).
4. Costo de las acciones comunes.
El costo de las acciones comunes es el rendimiento requerido por los inversionistas de mercado
sobre las acciones. Existen dos formas de financiamiento de las acciones comunes (1) utilidades
retenidas y (2) nuevas emisiones de acciones comunes. Como primer paso para calcular ambos
casos, debe estimarse el costo de capital de las acciones comunes.
Cálculo del costo de capital de las acciones comunes.
El costo de capital de las acciones comunes, ks, es la tasa a la cual los inversionistas descuentan
los dividendos esperados de la empresa a fin de determinar el valor de sus acciones. Se encuentran
disponibles dos técnicas para medir el costo de capital de las acciones comunes. Uan emplea el
modelo de valuación de crecimiento constante; la otra se base en el modelo de asignación de precio
del activo de capital (MAPAC).
Empleo del modelo de valuación de crecimiento contante (de Gordon)
Este modelo se basa en la premisa (ampliamente aceptada) de que el valor de una acción es igual al
valor presente de todos los dividendos futuros, que se espera proporcione ésta a lo largo de un
período infinito. La expresión clave que se utiliza en la siguiente ecuación:
Donde
Po = Valor de las acciones comunes.
D1 = Dividendo por acción especial esperado al final del año 1.
ks = Rendimiento requerido sobre las acciones comunes.
g = Tasa constante de crecimiento en dividendos.
Al resolver la anterior ecuación para despejar ks se obtiene la siguiente expresión del costo de
capital de las acciones comunes:
La anterior ecuación indica que el costo de capital de las acciones comunes puede calcularse al
dividir los dividendos esperados al cabo del año 1 entre el precio actual de las acciones, y sumando
esto la tasa de crecimiento esperada. Puesto que los dividendos de las acciones comunes pagados
a partir de los ingresos después de impuestos, no es necesario realizar el ajuste fiscal.
Ejemplo.
Aceros S.A. desea determinar su costo de capital de las acciones comunes ks. El valor de mercado,
Po, de sus acciones comunes es de $ 50 por unidad. La empresa espera pagar un dividendo, D1, de
$ 4 al final del año siguiente, en 2013. Los dividendos pagados sobre las acciones en circulación,
durante los seis años anteriores (2007-2012) fueron los siguientes:
Año
2007
2008
2009
2010
2011
2012
Dividendo
$ 3.80
3.62
3.47
3.33
3.12
2.97
Calculando la tasa de crecimiento anual de dividendos, g. Ésta resulta aproximandamente de 5%
(con más exactitud es de 5.05%). Al sustituir D1 = $ 4, Po = $ 50 y g = 5% en la ecuación se obitiene
el costo de capital de las acciones comunes:
El costo de capital de las acciones comunes, de 13%, representa el rendimiento requerido por los
accionistas actuales sobre la inversión, a fin de dejar inalterado el precio de mercado de las acciones
en circulación de la empresa.
Empleo del modelo de asignación de precio del activo de capital (MAPAC).
El modelo de asignación del activo de capital (MAPAC) describe la relación existente entre el
rendimiento requerido, o costo de capital de las acciones comunes, ks, y el riesgo no diversificable
de la empresa medido por el coeficiente beta, b. La expresión básica del MAPAC, se representa en
la siguiente ecuación:
Donde
RF = tasa de rendimiento libre de riesgo.
km = rendimiento de mercado; rendimiento sobre la cartera del mercado de activos.
Mediante el MAPAC, el costo de capital de las acciones comunes es el rendimiento requerido por los
inversionistas, como compensación por el riesgo no diversificable de la empresa, el cual es medido
por el coeficiente, b.
Ejemplo.
Aceros S.A., la cuál calculó en el ejemplo anterior el costo de su capital de las acciones comunes,
ks, usando el modelo de valuación de crecimiento constante, desea calcular este costo, por medio
del modelo de asignación de precio de activo de capital. Con base en la información obtenida a partir
de los asesores de inversiones de la empresa y de sus propios análisis, se ha determinado que la
tasa libre de riesgo, RF, es igual a 7%, que el coeficiente de beta, b, de la empresa es de 1.5, y el
rendimiento de mercado, km, de 11%. Al sustituir dichos valores en la anterior ecuación, la compañía
estima que el costo de capital de las acciones comunes, ks, es el siguiente:
El costo de capital de 13% del capital de las acciones comunes equivalentes al obtenido con el
modelo de valuación de crecimiento constante, representa el rendimiento requerido de los
inversionistas en las acciones comunes de Aceros S.A.
Costo de las utilidades retenidas.
Si las utilidades no fueran retenidas, serían distribuidas en pago, como dividendos, a los accionistas
comunes. En consecuencia, el costo de las utilidades retenidas, kr, es, para la empresa, similar al
costo de una emisión totalmente suscrita equivalente de acciones comunes adicionales. Esto
significa que las utilidades retenidas incrementan el capital contable de la misma manera que una
nueva emsión de acciones comunes. Los accionistas encuentran aceptable la retención de
utilidades, por parte de la empresa, sólo si esperan que ésta llegue a ganar, al menos, el rendimiento
que requieren éstos sobre los fondos reinvertidos.
Al considerar las utilidades retenidas como una emisión totalmente suscrita de acciones comunes
adicionales, se puede establecer el costo de utilidades retenidas para la empresa, kr, equiparable al
costo de capital de las acciones comunes, como se proporcionó en las anteriores ecuaciones:
No hay necesidad de realizar ajuste alguno por el costo de emisión sobre el costo de las utilidades
retenidas, puesto que, mediante las utilidades retenidas, la empresa adquiere capital sin incurrir en
costos de este tipo.
Ejemplo.
El costo de las utilidades retenidas de Aceros S.A. se calculó en los ejemplos anteriores, puesto que
éste es igual al costo de capital de las acciones comunes. En consecuencia, kr, equivale a 13.0%.
Como se mostrará en la sección siguiente, el costo de las utilidades retenidas es siempre menor que
el costo de una nueva emisión de acciones comunes, debido a la ausencia del costo de emisión en
los casos en que se financian proyectos con utilidades retenidas.
Costo de nuevas emisiones de acciones comunes.
El propósito es calcular el costo de capital total de la empresa es determinar el costo después de
impuestos de los nuevos fondos requeridos para el financiamiento de proyectos. Debe prestarse
atención, en consecuencia, al costo de una nueva emisión de acciones comunes, kn. Tal costo se
determina al calcular el costo de las acciones comunes, después de considerar tanto el monto de la
subvaluación como los costos de emisión asociados. Por lo general, a fin de vender una nueva
emsión de acciones, tendrá que recurrirse a una subvaluación; es decir, vendería a un precio por
debajo del de mercado actual, Po. Además, los costos de emisíon pagados y de la venta de la nueva
emisión reducirán los ingresos.
El costo de las nuevas emisiones puede calcularse al determinar los valores netos de realización
después de los costos de subvaluación y de emisión, mediante la expresión del modelo de valuación
de crecimiento constante, para obtener el costo de las acciones comunes existentes, ks, que será
como punto de partida. Si se deja a Nn representar los valores netos de realización por la venta de
las nuevas acciones comunes, después de considerar los costos de subvaluación y de emisión, el
costo de la nueva emisión, kn, puede expresarse de la forma siguiente:
Como los valores netos de realización por la venta de las nuevas acciones comunes, Nn, serán
menos que el precio del mercado actual, Po, el costo de las nuevas emisiones kn, serán siempre
mayor que el costo de las emisiones existentes, ks, el cual, como se señalo, es equivalente al costo
de utilidades retenidas, kr. El costo de las nuevas acciones comunes suele ser mayor que cualquier
otro costo de financiamiento a largo plazo. Debido a que los dividendos de las acciones comunes se
pagan a partir de los flujos de efectivo después de impuestos, no resulta necesario llevar a cabo
ajuste alguno.
Ejemplo.
En el ejemplo que incluyó el modelo de valuación de crecimiento constante se emplearon para
calcular el costo de capital de acciones comunes de Aceros S.A., los valores del dividendo esperado,
D1, de $ 4; el precio de mercado actual, Po, de $ 50 y la tasa de crecimiento de dividendos esperada,
g, de 5%. El valor obtenido del costo mencionado inicialmente fue de 13.0%. A fin de determinar el
costo de las nuevas acciones comunes, kn, Aceros S.A. con ayuda de sus asesores ha estimado
que las nuevas acciones puede ser vendidas en promedio a $ 47. La subvaluación de $ 3 resulta
necesaria, debido a la naturaleza competitiva del mercado. Un segundo costo relacionado con la
nueva emisión es la tarifa de suscripción de $ 2.50 por acción, la cual se pagaría para cubrir los
costos de emisión y de venta de la nueva emisión. En consecuencia, se espera que los costos
totales de subvaluación y emisión por acción sean de $ 5.50.
Al restar el costo de subvaluación y de emisión de $ 5.50 por acción al precio actual, Po, de $ 50, se
obtienen los valores netos de realización esperados, Nn de $ 44.50 por acción ($ 50.00 – $ 5.50). Si
se sustituyen D1 = $ 4, Nn = $ 44.50 y g = 5% en la ecuación siguiente, se obtiene el siguiente costo
de las nuevas emisiones comunes, kn:
El costo de las nuevas acciones, kn, de Aceros S.A., es por tanto de 14.0%. Este es el valor que se
usará en el cálculo subsecuente del costo de capital total de la empresa.
5. Costo de capital promedio ponderado (CCPP).