1.- Halle el circuito equivalente de Norton entre los

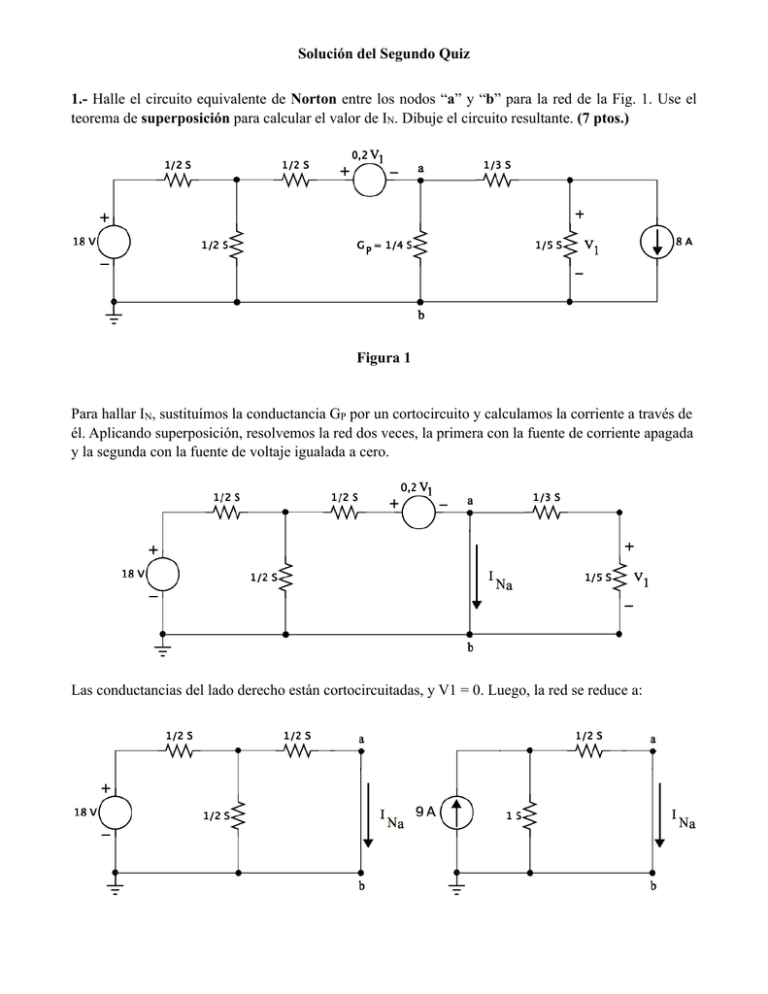
Solución del Segundo Quiz
1.- Halle el circuito equivalente de Norton entre los nodos “a” y “b” para la red de la Fig. 1. Use el
teorema de superposición para calcular el valor de IN. Dibuje el circuito resultante. (7 ptos.)
Figura 1
Para hallar IN, sustituímos la conductancia GP por un cortocircuito y calculamos la corriente a través de
él. Aplicando superposición, resolvemos la red dos veces, la primera con la fuente de corriente apagada
y la segunda con la fuente de voltaje igualada a cero.
Las conductancias del lado derecho están cortocircuitadas, y V1 = 0. Luego, la red se reduce a:
INa = 9 !
1
=3A
3
Apagando ahora la fuente de 18 V:
Calculamos I2 y V1 por divisor de corriente:
13
40
I2 = 8 !
=
=5A
13+15 8
V1 = –
I2
= –15 V
1/ 3
Además :
0,2 V1
= 1A
3
= 1 – 5 = –4 A
3I1 + 0,2V1 = 0
!
I1 = –
INb = I1 – I2
!
INb
Finalmente, IN = INa + INb = 3 – 4 = –1 A /////
Para hallar la conductancia equivalente, sustituímos GP por una fuente de prueba, apagando ambas
fuentes independientes. La red se reduce a:
GN =
Ip
Ip = I1 + I2
Vp
Vp = 8I2
V1 = 5I2 =
!
5Vp
8
Vp = 3I1 – 0,2V1 = 3I1 –
1$
!
Vp # 1 + & = 3I1
"
8%
Ip =
La red equivalente buscada es:
3Vp
8
+
Vp
8
=
Vp
2
'
I1 =
!
GN =
3Vp
8
1
S /////
2
I2 =
Vp
8
Vp
8
2.- En el circuito de la Fig. 2, hallar el valor de la resistencia RL para que ésta disipe la máxima
potencia posible, y calcule el valor de esa potencia máxima (usar el teorema de Thevenin). (8 ptos.)
Figura 2
El teorema de máxima trasferencia de potencia dice que se necesita RL = RTh. Para hallar RTh,
sustituímos RL por una fuete de prueba, e igualamos a cero las fuentes independientes:
Reducimos esta red y resolvemos para Ip:
!12I1 – 4I2 = –10V2 + 4I1
#
" – 4I1 +13I2 – 8I3 = 0
# –8I + 8I = –V
3
p
$ 2
V2 = I2
!8I1 + 6I2 = 0
#
" – 4I1 +13I2 – 8I3 = 0
# –8I + 8I = –V
3
p
$ 2
De (1) y (2):
Combinando con (3):
4I1 + 3I2 = 0
– 4I1 +13I2 – 8I3 = 0
16I2 – 8I3 = 0
Ip = –I3 =
R Th =
Vp
Ip
(1)
(2)
(3)
8I2 – 4I3 = 0
–8I2 + 8I3 = –Vp
4I3 = –Vp
Vp
4
=4!
!
R L = 4 ! /////
Para calcular la potencia máxima, necesitamos hallar la tensión equivalente de Thevenin, es decir, el
voltaje a circuito abierto entre “a” y “b”:
" 12 !4 % " I1 % "12 ! 10V2 + 4I1 %
$ !4 13 ' $ I ' = $
'
!16
#
& # 2& #
&
V2 = I2
VTh = 16 + 8I2
" 8 6 % " I1 % " 12 %
$ !4 13' $ I ' = $ !16 '
#
& # 2& #
&
!=
8 6
= 104 + 24 = 128
– 4 13
8
12
– 4 "16
–128 + 48
–80
5
I2 =
=
=
=–
!
128
128
8
# 5&
VTh = 16 + 8 % – ( = 11 V /////
$ 8'
VR L = VTh
PR L =
VR2L
RL
RL
4 11
= 11! =
V
R Th + R L
8
2
=
(11 2 )2
4
=
121
W /////
16