1. Deberás recordar
Anuncio

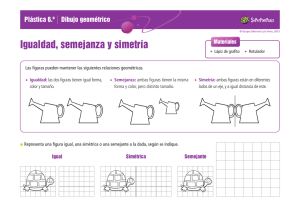
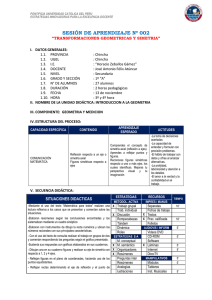
unidad 11 Transformaciones geométricas Cómo dibujar ángulos de 60° con regla y compás La cuerda de un arco de 60° (apertura del compás) es igual al radio con que se ha trazado. Veamos el proceso: Así se traza un ángulo de 60° de vértice V y lado l. l V l V l V 60° actividades 1 Dibuja en tu cuaderno, ayudándote del compás, algunos ángulos de 60°. Página 1 unidad 11 Transformaciones geométricas Cómo trazar ángulos rectos sobre papel cuadriculado (con los lados no paralelos a las líneas de la cuadrícula) Observa cómo se traza, en cada caso, un ángulo recto de vértice V y lado l : a c b l l l 90° 90° V 90° V V El caso a) es muy fácil. Para los casos b) y c), conviene tener en cuenta la igualdad de los triángulos señalados que, como es natural, en la práctica no hace falta señalar expresamente. actividades 2 Dibuja en tu cuaderno, apoyándote en la cuadrícula, varios ángulos de 90°. Página 2 unidad 11 Transformaciones geométricas Cómo representar puntos y rectas en un sistema de ejes cartesianos Las expresiones analíticas de las rectas son ecuaciones de primer grado en x e y. Por ejemplo: y = 2x – 3, y = x, y = 5, x = 0, y = 0 •Para representar una recta, basta con obtener dos de sus puntos. y = 2x + 3 x = 0 8 y = 3 x = 2 8 y = 7. La recta pasa por (0, 3) y (2, 7) •Hay algunas rectas muy sencillas que deberías ser capaz de reconocer de un solo golpe de vista. y=2 y=x x = 0 es el eje Y y = 0 es el eje X actividades 3 Representa: a) y = x – 4 b) y = 5x – 10 c) y = 4 d) x = –3 e) y = –x Página 3 unidad 11 Transformaciones geométricas Figuras simétricas. Ejes de simetría En la naturaleza, en la técnica, en el arte, en nuestro mundo cotidiano estamos rodeados de figuras simétricas. Su estudio es interesante. E J E DE SIMETRÍA DE UNA FIGURA Una figura plana es simétrica respecto a una recta si al doblarla por dicha recta las dos mitades coinciden. e A A' B B' En una simetría respecto a un eje o simetría axial: • La recta e se llama eje de simetría. • A y A' son simétricos respecto a e, porque e es la mediatriz del segmento AA'. Lo mismo ocurre con B y B'. •C ada punto del eje es simétrico de sí mismo: C = C'. C = C' La simetría de las figuras planas se aprecia a simple vista y suele ser sencillo identificar su eje de simetría. No obstante, puede ser de gran ayuda valerse de un espejo para comprobar si una cierta recta es o no eje de simetría de una figura. Las siguientes figuras tienen dos, tres y cinco ejes de simetría, respectivamente: 90 36 60 Si una figura tiene n ejes de simetría, estos se cortan en un punto, y cada dos ejes conti180° . guos forman un ángulo de n actividades 1 Señala todos los ejes de simetría de cada una de las siguientes figuras. a) b) c) d) e) Página 4 unidad 11 Transformaciones geométricas Cómo dibujar ángulos de 60° con regla y compás Soluciones La cuerda de un arco de 60° (apertura del compás) es igual al radio con que se ha trazado. Veamos el proceso: Así se traza un ángulo de 60° de vértice V y lado l. l V l V l V 60° actividades 1 Dibuja en tu cuaderno, ayudándote del compás, algunos ángulos de 60°. Respuesta abierta. Página 1 unidad 11 Transformaciones geométricas Cómo trazar ángulos rectos sobre papel cuadriculado (con los lados no paralelos a las líneas de la cuadrícula) Soluciones Observa cómo se traza, en cada caso, un ángulo recto de vértice V y lado l : a c b l l l 90° 90° V 90° V V El caso a) es muy fácil. Para los casos b) y c), conviene tener en cuenta la igualdad de los triángulos señalados que, como es natural, en la práctica no hace falta señalar expresamente. actividades 2 Dibuja en tu cuaderno, apoyándote en la cuadrícula, varios ángulos de 90°. Respuesta abierta. Página 2 unidad 11 Transformaciones geométricas Cómo representar puntos y rectas en un sistema de ejes cartesianos Soluciones Las expresiones analíticas de las rectas son ecuaciones de primer grado en x e y. Por ejemplo: y = 2x – 3, y = x, y = 5, x = 0, y = 0 •Para representar una recta, basta con obtener dos de sus puntos. y = 2x + 3 x = 0 8 y = 3 x = 2 8 y = 7. La recta pasa por (0, 3) y (2, 7) •Hay algunas rectas muy sencillas que deberías ser capaz de reconocer de un solo golpe de vista. x = 0 es el eje Y y=2 y=x y = 0 es el eje X actividades 3 Representa: a) y = x – 4 a) b) y = 5x – 10 c) y = 4 b) Y d) x = –3 e) y = –x c) Y Y y=4 y=x–4 (4, 0) X (2, 0) X X y = 5x – 10 (0, –4) (0, –10) d) e) Y Y X X y = –x x = –3 Página 3 unidad 11 Transformaciones geométricas Figuras simétricas. Ejes de simetría Soluciones En la naturaleza, en la técnica, en el arte, en nuestro mundo cotidiano estamos rodeados de figuras simétricas. Su estudio es interesante. E J E DE SIMETRÍA DE UNA FIGURA Una figura plana es simétrica respecto a una recta si al doblarla por dicha recta las dos mitades coinciden. e A A' B B' En una simetría respecto a un eje o simetría axial: • La recta e se llama eje de simetría. • A y A' son simétricos respecto a e, porque e es la mediatriz del segmento AA'. Lo mismo ocurre con B y B'. •C ada punto del eje es simétrico de sí mismo: C = C'. C = C' La simetría de las figuras planas se aprecia a simple vista y suele ser sencillo identificar su eje de simetría. No obstante, puede ser de gran ayuda valerse de un espejo para comprobar si una cierta recta es o no eje de simetría de una figura. Las siguientes figuras tienen dos, tres y cinco ejes de simetría, respectivamente: 90 36 60 Si una figura tiene n ejes de simetría, estos se cortan en un punto, y cada dos ejes conti180° . guos forman un ángulo de n actividades 1 Señala todos los ejes de simetría de cada una de las siguientes figuras. a) b) c) d) e) Página 4