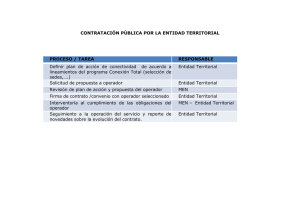
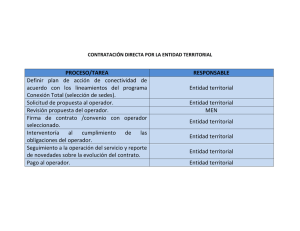
Cap. 4

Capítulo 4
ENTROPÍA Y ENSEMBLES DE EQUILIBRIO DE LA
ESTADÍSTICA CUÁNTICA
4.1
Operador de entropía.
En la mecánica estadística cuántica, por analogía con la estadística clásica se introduce un operador de entropía
b́= ¡ ln (b
½ ):
(4.1)
Sabemos que b
½ es un operador hermitiano definido positivo. Su logaritmo es hermitiano y el operador b́también es definido positivo. En efecto, si w 1 ;w 2 ;:::w n ;:::, son los
autovalores de b
½ , donde w n · 1 8 n = 1 ;2 ;:::, entonces ¡ ln w 1 ;¡ ln w 2 ;:::¡ ln w n ;:::,
son los autovalores de b́. Esto es debido a la conocida propiedad: los autovalores de una función del operador son iguales a la función de los autovalores (i.e.,
Ab' k = a k ' k ) f (Ab)' k = f (a k )' k ).
El operador de entropía tiene la propiedad aditiva que hemos comentado en
relación con la entropía de la información (cap.1, II parte). Supongamos que el
sistema se puede subdividir en dos partes, de carácter independiente una de la otra
(o sea, debilmente acopladas). Entonces la probabilidad de una configuración del
sistema total es el producto de las probabilidades de las configuraciones de los dos
subsistemas. El operador b
½ es el producto directo de dos operadores ½b1 , ½b2 , que
describen por separado cada subsistema
b
½ = ½b1 − ½b2 :
(4.2)
En la representación matricial, el producto directo de operadores Cb = Ab− Bb se define
mediante la expresión
c jl = a ik b i0k 0;
(4.3)
donde los índices
i.e.,hj = ii0i
, l = k k 0 y las matrices se definen
h i j,l, son compuestos,
h i
como sigue: Ab = a ik , Bb 0 0 = b i0k 0, Ab− Bb = c jl. El lector tambien puede
ik
ik
jl
considerar que c jl = c ii0k k 0 es un tensor de cuarto rango, formado por el producto
exterior de dos tensores de rango dos. Cuando la 4.2 es válida, resulta
b́= b́1 + b́2 ;
(4.4)
½ ® ), con ® = 1 ;2 .
donde b́® = ¡ ln (b
El operador de entropía, como el operador estadístico, también satisface la
ecuación 3.66
@ b́ h i
(4.5)
i~ = Hb;b́ ;
@t
Invariancia temporal de la entropía de Gibbs
51
como es fácil de comprobar. En efecto, dado que b́ es una serie de potencias de b
½,
basta ver que las potencias de b
½ también satisfacen la ecuación 3.66. Por ejemplo,
h
i
@b
½b
½
b
i~
= H ;b
½b
½ ;
@t
(4.6)
porque el conmutador tiene la siguiente propiedad
h
i h i
h i
Hb;b
½b
½ = Hb;b
½ b
½+ b
½ Hb;b
½ :
(4.7)
En general, b
½ n también satisface la ecuación
i
h
@b
½n
i~
= Hb;b
½n
@t
(4.8)
y, por lo tanto, cualquier función de operadores que se represente como serie de
potencias de b
½ satisface la misma ecuación de evolución . La utilidad de la 4.5 estriba
en que, tanto Hb cuanto b́, son operadores hermitianos aditivos para subsistemas
debilmente acoplados.
El valor medio del operador de entropía define la entropía de Gibbs (cap1, II
parte) para un sistema cuántico
S = hb́i = ¡ hln (b
½ )i = ¡ Tr (½ ln (½ )):
(4.9)
Debido a las propiedades de la matriz densidad la entropía es positiva definida, porque
en la representación diagonal de b
½ tenemos
X
½ n n ln (½ n n ) ¸ 0 ;
(4.10)
S = ¡
n
y esto es debido a que los autovalores de b
½ son tales que ½ n n ¸ 0 8 n . La entropía S es
nula sólo cuando b
½ describe un estado puro (como hemos mencionado en el capítulo 3,
II parte). La entropía tiene la propiedad aditiva: si b
½ describe un ensemble compuesto
por dos ensembles estadísticamente independientes y si b
½ es el producto directo de
dos operadores ½b1 , ½b2 , como en 4.2, entonces S = S 1 + S 2 , donde S ® = ¡ hln (b
½ ® )i,
® = 1 ;2 , debido a la vigencia de 4.4 y la linealidad de la operación de promedio.
4.2
Invariancia temporal de la entropía de Gibbs
Podemos comprobar que la entropía de Gibbs de un sistema aislado no cambia con el
tiempo. Partimos de la solución formal ½ (t) = U (t;0 )½ (0 )U ¡1 (t;0 ) 3.83 y calculamos
la entropía al tiempo t,
S (t) =
¡ Tr [½ (t) ln (½ (t))] =
¡
£
¡ Tr U (t;0 )½ (0 )U ¡1 (t;0 ) ln U (t;0 )½ (0 )U
¡1
(t;0 )
¢¤
:
(4.11)
A este punto, invocamos una propiedad general de las funciones de operadores
¤
£
(4.12)
f U (t;0 )½ (0 )U ¡1 (t;0 ) = U (t;0 )f [½ (0 )]U ¡1 (t;0 );
Ensembles de equilibrio en la estadística cuántica
52
la cual se demuestra inmediatamente a partir de la representación de f en serie
de potencias del argumento. En particular, aplicamos esta propiedad al caso del
logaritmo y por lo tanto
¤
£
(4.13)
S (t) = ¡ Tr U (t;0 )½ (0 )U ¡1 (t;0 )U (t;0 ) ln (½ (0 )) U ¡1 (t;0 ) :
Naturalmente, U U ¡1 = 0 y además al calcular la traza de un producto de operadores
podemos permutar cíclicamente los factores, i.e.,
Finalmente, obtenemos
Tr (AbBbCb) = Tr (CbAbBb) = Tr (BbCbAb):
(4.14)
S (t) = ¡ Tr [½ (0 ) ln (½ (0 ))] = S (0 ):
(4.15)
También en el caso de la física cuántica surge el problema que ya habíamos
encontrado en la física clásica, la entropía de Gibbs no varía en el tiempo y por lo
tanto no puede describir la tendencia irreversible hacia el equilibrio termodinámico,
como se observa en la naturaleza. Por otra parte, como sabemos, la entropía de
Gibbs es una noción muy eficaz para el tratamiento de equilibrios y que corresponde
bien con la noción de entropía de la termodinámica de estados de equilibrio. La
solución de esta dificultad, muy debatida y todavía no completamente asentada, se
examina en las monografías avanzadas de procesos fuera de equilibrio, introduciendo
una distinción entre promedios del tipo de grano ”fino” y de grano ”grueso”, cuya
necesidad ya había sido advertida por el mismo Gibbs y sobre la cual no podemos
detenernos.
4.3
Ensembles de equilibrio en la estadística cuántica
Presentamos ahora el formalismo cuántico para tratar los ensembles de equilibrio y
su relación con la termodinámica. En el equilibrio la matriz densidad sólo puede
depender de integrales de movimiento del sistema que sean aditivas. Tal como en
mecánica clásica, para un sistema genérico se conocen tres integrales del movimiento
¡!
de esa clase, Hb, el operador de la energía (supuesto independiente del tiempo) Pb,
¡!
el operador del momento lineal y Mc , el operador del momento angular. Los tres
nombrados son operadores hermitianos que actúan sobre ª (¡x! 1 ; ¡x! 2 ;:::; ¡!
x N ). Por consiguiente y siempre en consonancia con la noción de ensemble de Gibbs vista en el
límite clásico, el operador estadístico debe ser función de los tres operadores citados
¡! ¡!
b
½ = b
½ (Hb; Pb; Mc );
(4.16)
cuando el número de partículas está prefijado y no cambia de un miembro a otro
del ensemble. Cuando, en cambio, el número de partículas puede variar (no está
prefijado) entonces hay que introducir un operador adicional Nb, cuyos autovalores
dan los valores observables del número de componentes del sistema. En el equilibrio
Nb debe ser un invariante del movimiento, es decir,
[Nb; Hb] = 0 ;
(4.17)
La distribución microcanónica
53
y por lo tanto conmuta con Hb. La función de onda ª
autofunción de ambos operadores
Hbª
® ;N
= E
® ;N
ª
® ;N
Nbª
;
® ;N
® ;N
del estado es simultáneamente
= N ª
® ;N
;
(4.18)
y el número de partículas se puede medir exactamente junto con la energía. El
operador estadístico es ahora una función de los siguientes operadores
¡! ¡!
b
½ = b
½ (Hb; Pb; Mc ; Nb):
(4.19)
¡!
¡!
Cuando el sistema está contenido en un recipiente en reposo y no rota, P = M = 0
y no es necesario tener en cuenta los correspondientes operadores ya que toman el
mismo valor en todos los miembros del ensemble.
En la descripción por poblaciones de un sistema compuesto por elementos
iguales debilmente acoplados (ver cap. 6 y 7, I parte) se asignan números de partículas
n i para cada estado de partícula única i, cuya energía es " i, siendo i = 1 ;2 ;:::, el índice
que etiqueta los estados (incluyendo degeneración si la hubiera). Aquí, el operador
de energía de partícula única b
h tiene por autovalores las energías " i. En este caso
se introducen operadores nbi cuyos autovalores son los números de ocupación de cada
estado i y se escribe
X
Nb =
nbi;
(4.20)
i
para el número total de partículas. Asimismo, escribimos
X
" inbi;
Hb =
i
(4.21)
para la energía total. En general, Nb es un operador independiente de Hb, puesto que
podemos cambiar la energía del sistema pasando una partícula de un estado i a otro
j tal que " i 6= " j sin modificar el número de partículas.
Resumiendo: a) cuando el número de partículas es fijo tenemos
b
½ = b
½ (Hb);
(4.22)
b
½ = b
½ (Hb; Nb):
(4.23)
mientras que b) cuando el número de partículas puede variar, resulta
Naturalmente, b
½ puede depender también de otros parámetros macroscópicos que
especifican todo el ensemble, como el volumen, el campo magnético, etc..
4.4
La distribución microcanónica
Como en el caso clásico, esta distribución caracteriza un sistema aislado. El volumen
V u otros parámetros del sistema, están especificados y el número de partículas
N está prefijado. El ensemble tiene una energía total comprendida en el intervalo
(E ;E + ¢ E ) con ¢ E ¿ E y los estados de todos los miembros del ensemble son
equiprobables
¾
½
1
E · E® · E + ¢ E ;
− (E ;N ;V )
w (E ® ) =
(4.24)
0
si E ® < E o E + ¢ E < E ® :
La distribución microcanónica
54
Este es un postulado fundamental de la mecánica estadística, ya discutido en los
capítulos: 1, I parte y 1, II parte. Una diferencia con el caso clásico es que − (E ;N ;V )
no es simplemente el volumen de espacio de fase comprendido en el estrato de energía
(E ;E + ¢ E ) sino el numero de estados cuánticos ® comprendidos en la condición
E · E ® · E + ¢ E . Este número se denomina peso estadístico asociado con la energía
E . Para un sistema aislado, − (E ;N ;V ) representa la multiplicidad o degeneración
del nivel de energía total E cuando el volumen es V y el número de partículas vale
N . En la representación de matriz x el operador estadístico microcanónico toma la
forma
X
1
½ (x ;x 0) =
ª ® (x )ª ¤® (x 0);
(4.25)
− (E ;N ;V ) 1 ·® ·−
x N ; ¡¾! 1 ; ¡¾! 2 ;:::; ¡!
¾ N g y ª 1 (x );ª 2 (x );:::ª − (x ), son
donde, en general, x ! f ¡x! 1 ; ¡x! 2 ;:::; ¡!
b
las autofunciones de H correspondientes al nivel degenerado E .
La segunda diferencia es que en el caso cuántico, el postulado básico se completa con un agregado sin contraparte clásica. Las fases de las amplitudes de probabilidad de los estados ª ® (x ) se distribuyen al azar en el ensemble de equilibrio. Ya
hemos encontrado esta noción en la última sección del cap.3, II parte.
Recapitulemos algunos conceptos a fin de entender mejor esta cuestión. Si el
sistema se halla en un estado
X
ª (x ) =
c ® ª ® (x );
(4.26)
1 ·® ·−
como superposición de autoestados de la energía, entonces las c ® son amplitudes de
probabilidad de encontrar el sistema en el estado ª ® y jc ® j2 las respectivas probabilidades (suponiendo que ª (x ) está normalizada). Al medir un oservable Ab, el valor
medio de un gran número de mediciones repetidas vale
³
´ X
X
A = (ª ; Abª ) =
c ¤® 0c ® ª ® 0; Abª ® =
c ¤® 0c ® A ® ;® 0:
(4.27)
® ;® 0
® ;® 0
Pero, cuando se estudia un sistema (macroscópico) con un gran número de
componentes el conocimiento de una determinación completa del sistema como en 4.26
es algo que escapa absolutamente a nuestras posibilidades. Lo que hacemos, entonces,
es trabajar con promedios de la ecuación 4.27 sobre el ensemble que representa nuestro
conocimiento incompleto
E X
−® D
A = (ª ; Abª ) =
hc ¤® 0c ® i A ® ;® 0;
(4.28)
® ;® 0
(el cual, por otra parte, equivale al promedio temporal en el curso de una medición,
ver sección capítulo 3, II parte). Luego postulamos: a) una distribución al azar de
las fases de las amplitudes de probabilidad
hc ¤® 0c ® i = 0
si ® 6= ® 0;
(4.29)
y por otro lado (b) hc ¤® c ® i = w (E ® ) = 1 = − (E ;N ;V ) como en 4.24, es decir, una
probabilidad uniforme para todos los estados del estrato de energía (E ;E + ¢ E ). Con
La distribución canónica
55
− ®
P
los postulados a) y b) resulta, naturalmente, A = < (ª ; Abª ) > =
w (E ® )A ® ;® =
®
P
½ Ab).
[1 = − (E ;N ;V )] A ® ;® = Tr (b
®
−®
Resumiendo, para obtener valores medios A de observables de sistemas en
equilibrio operamos
con una combinación lineal no coherente de autoestados de la
P
energía, ª 0 =
b
ª
® ® ® (en lugar de un estado puro como en la ecuación 4.26) en la
2
cual jb ® j = w (E ® ) y donde las fases Á ® de b ® = r ® ex p (iÁ ® ) están distribuidas al azar,
hÁ ® i = 0 , hex p (iÁ ® )i = 0 . El postulado estadístico cuántico de un sistema aislado
pide,−entonces,
dos cosas: equiprobabilidad y fases al azar. Se puede pensar, luego,
®
que A resulta de la expresión (ª 0; Abª 0); empleando la combinacíon no coherente ª 0,
que por brevedad llamamos estado mezcla (aunque no es un estado cuántico, como
ya notamos).
El operador estadístico también se puede escribir como
³
´
1
b
½ =
¢ Hb ¡ E ;
(4.30)
− (E ;N ;V )
donde Hb = Hb(b
p ; qb) es el operador de energía del sistema, mientras que ¢ (x ) es la
función
¾
½
1 0· x · ¢ E
(4.31)
¢ (x ) =
0 si x < 0 o x > ¢ E .
Como en el caso clásico, la equiprobabilidad del ensemble microcanónico, así como la
distribución de fases al azar, es plausible, pero no ha sido rigurosamente demostrada.
Los estudios orientados a justificar esta hipótesis constituyen el problema ergódico de
la estadística cuántica.
Empleando la representación diagonal del operador estadístico encontramos
que
X
S = h´ i = ¡ Tr (½ ln (½ )) = ¡
w ® ln (w ® ) ;
(4.32)
®
pero, dado que en el estrato ¢ E de energía todas las probabilidades son iguales,
resulta
S = ln (− (E ;N ;V )):
(4.33)
Se han reobtenido formalmente las fórmulas fundamentales de la entropía estadística
de los capítulos 1 y 4, I parte y 2, II parte. La última expresión es la célebre fórmula
de Boltzmann, válida para el equilibrio microcanónico. Como sabemos, esta fórmula
no es la más conveniente en la práctica para obtener la termodinámica de un sistema,
salvo casos simples el cálculo de − (E ;N ;V ) es un problema complicado.
4.5
La distribución canónica
El ensemble canónico representa un sistema con un número fijo de partículas N y
volúmen V constante (u otros parámetros específicos de cada sistema) el cual está abierto al intercambio de calor con un baño térmico a temperatura prefijada T .
La distribución de probabilidades de estados ® en este ensemble está dada por las
fórmulas
X
E®
1
E®
w® =
ex p (¡
); Z (µ ;V ;N ) =
);
(4.34)
ex p (¡
®
Z (µ ;V ;N )
µ
µ
La distribución canónica
56
donde µ = k T . La sumatoria en Z se realiza sobre todos los estados ® permitidos
por las condiciones de simetría o antisimetría correspondientes a cada familia de
partículas. Como sabemos, los estados ® pueden ser degenerados, o sea, ser distintos
y tener la misma energía.
La energía libre para este ensemble vale
F (µ ;V ;N ) = ¡ µ ln [Z (µ ;V ;N )]
(4.35)
y la matriz densidad se representa con
½ (x ;x 0) =
X
1
Z (µ ;V ;N )
®
ex p (¡
E
®
µ
)ª ® (x )ª ¤® (x 0);
(4.36)
donde ª ® (x ) son las autofunciones de Hb. En la notación compacta, como operador
cuántico que es función de otros operadores, escribimos
b
½ =
Hb
(F ¡ Hb)
1
ex p (¡ ) = ex p [¡
];
Z (µ ;V ;N )
µ
µ
(4.37)
mientras que para la función de partición podemos emplear la expresión
X
Hb
Z (µ ;V ;N ) = Tr [ex p (¡ )] =
µ
®
Z
ª ® (x ) ex p (¡
Hb ¤
)ª ® (x )d x :
µ
(4.38)
Esta fórmula es muy conveniente por la invariancia de la traza frente a cambios de
representación de las matrices. No depende de la elección particular de las funciones
de base ª ® (x ), las cuales no precisan ser autofunciones de Hb, aunque en este último
caso el cálculo se simplifica y se reduce a la fórmula habitual para Z (µ ;V ;N ) que
hemos empleado en la primera parte de estas notas.
Las ideas básicas de la derivación de la distribución canónica de los capítulos
2, I parte y 2, II parte, también pueden formularse con el formalismo de la mecánica
cuántica. Combinamos el sistema 1 con un baño térmico 2 en interacción débil, como
un único sistema aislado, de modo que el hamiltoniano del conjunto es
Hb = Hb1 + Hb2 + Hbin t ;
(4.39)
° °
°b °
°H 2 °. La interacción Hbin t es muy pequeña y la energía total es
prácticamente la suma de las energías de 1 y 2 . Recordamos que Hbin t no puede ser
nula, porque es necesario que los dos sistemas puedan intercambiar energía, aunque
en pequeñas dosis. Con estas condiciones la función de onda del sistema combinado
será, con gran precisión,
ª ik = ª k (x )© i(y );
(4.40)
° °
° °
donde °Hb1 ° ¿
donde ª k (x ) son las autofunciones de Hb1 y © i(y ) son las autofunciones de Hb2 y
además
E ik = E i + E k :
(4.41)
Propiedades extremales de los ensembles de equilibrio en la formulación cuántica
57
Dado que el sistema total está aislado tendremos una forma microcanónica para el
operador estadístico,
X
w ik ª ik (x ;y )ª ¤ik (x 0;y 0);
(4.42)
½ (x ;y ;x 0;y 0) =
i;k
donde
w
ik
=
½
1
−
0
E · E ik · E + ¢ E ;
si E ik < E o E + ¢ E < E
ik :
¾
(4.43)
La matriz densidad del sistema 1 se obtiene calculando la traza de b
½ sobre las coordenadas del baño térmico 2 ,
Z
X
0
0 0
½ (x ;x ) = Tr (2 ) [½ (x ;y ;x ;y )] =
w ik ª ik (x ;y )ª ¤ik (x 0;y )d y :
(4.44)
i;k
Al efectuar este cómputo, teniendo en cuenta que las © i(y ) son ortonormales, se
obtiene
X
½ (x ;x 0) =
w k ª k (x )ª ¤k (x 0);
(4.45)
k
donde hemos definido
w
k
=
X
i
w
ik
(4.46)
Por lo tanto, para hallar la distribución de probabilidades de los estados del
sistema 1 debemos sumar la función de probabilidad del sistema combinado sobre
todos los estados del baño térmico 2 . En fórmulas
X
X
1
;
(4.47)
w (E i + E k ) =
wk =
i
i − (E )
donde E = E i + E
entonces,
k
y por brevedad de notación omitimos V , N , en − (E ). Resulta,
w
k
=
− 2 (E ¡ E k )
;
− (E )
(4.48)
donde − 2 es el número de estados cuánticos del baño térmico correspondientes a la
energía E ¡ E k y − (E ) es el número de estados del sistema total con energía E . A
este punto la deducción de la distribución canónica sigue los mismos pasos dados en
el capítulo 2, I parte y no es necesario reiterarla.
4.6
Propiedades extremales de los ensembles de equilibrio en la formulación cuántica
4.6.1 Desigualdad auxiliar
Para demostrar las propiedades variacionales que siguen se emplea la desigualdad
ln (x ) ¸ 1 ¡ 1 = x , que se comprueba facilmente para los x reales positivos (ya mencionada en la sección 2.4, II parte). La igualdad rige sólo para x = 1 . La propiedad
se puede aplicar a cada componente de una sucesión discreta de valores positivos x j ,
j = 1 ;2 ;:::, en la forma
x j ln (x j ) ¸ x j (1 ¡ 1 = x j )
(4.49)
Propiedades extremales de los ensembles de equilibrio en la formulación cuántica
58
o bien a los valores continuos de una variable x , escribiendo x ln (x ) ¸ x (1 ¡ 1 = x ).
A partir de estas desigualdades podemos probar que para cualquier par b
½, b
½1,
de operadores estadísticos se cumple
Tr [b
½ ln (b
½ )] ¸ Tr [b
½ ln (b
½ 1 )]
(4.50)
y que la igualdad ocurre sólo cuando b
½ = b
½ 1 . En efecto, en el caso discreto empleando
la representación diagonal de b
½ ;b
½ 1 basta poner x j = ½ jj = ½ 1jj en la ecuación 4.49 y
observar que para todos los valores de ½ jj ;½ 1jj (necesariamente positivos puesto que
½ jj ;½ 1jj representan probabilidades) se cumple
½ jj
1
[ln (½ jj ) ¡ ln (½ 1jj )] ¸ 1 (½ jj ¡ ½ 1jj ):
1
½ jj
½ jj
Multiplicando por ½ 1jj y sumando sobre j se obtiene
X
X
[½ jj ln (½ jj ) ¡ ½ jj ln (½ 1jj )] ¸
(½ jj ¡ ½ 1jj ) = 0 ;
j
j
(4.51)
(4.52)
dado que la suma tanto de ½ jj cuanto de ½ 1jj es la unidad. La prueba para la representación en variable continua sigue el mismo camino.
4.6.2 Propiedad extremal de la matriz densidad microcanónica
Sea la representacíon matricial del operador estadistico
½ n m = (ª n ;b
½ª
m
) = w n ±n m
(4.53)
en la base completa de autofunciones de la energía, ª 1 ;ª 2 ;ª 3 :::. En equilibrio,
las probabilidades w n son funciones de la energía w n = w n (E n ). En el ensemble
microcanónico de un sistema aislado E · E n · E + ¢ E las probabilidades de todos
los estados accesibles son iguales, w n (E ) = 1 = − (E ). La matriz densidad ½ n m =
± n m = − (E ) corresponde a al máximo de la entropía de Gibbs frente a cualquier otra
matriz densidad de equilibrio ½ 1n m = w n (E )± n m .
Empleando la desigualdad 4.50 la demostración es muy simple:
S1 =
=
¡ k Tr [b
½ 1 ln (b
½ 1 )] · ¡ k Tr [b
½ 1 ln (b
½ )] = k ln (− (E ))Tr [b
½1]=
k ln (− (E )) = S :
(4.54)
4.6.3 El principio variacional de la matriz densidad del ensemble canónico
La matriz densidad del ensemble canónico corresponde a un extremo de la entropía
respecto de cualquier otra matriz densidad de equilibrio para un sistema con la misma
energía media y el mismo número de partículas. De la misma manera que para el caso
clásico del capítulo 2, II parte, el principio variacional se formula como un extremo
condicionado para la funcional
n
o
¤ (½ ) ´ k ¡ Tr [b
½ ln (b
½ )] ¡ ¯ Tr [b
½ Hb] ¡ ¸ Tr [b
½] ;
(4.55)
donde se han introducido dos multiplicadores de Lagrange, o sea,
± ¤ (½ ) = 0 ;
8 ±½:
(4.56)
Propiedades extremales de los ensembles de equilibrio en la formulación cuántica
Empleando la representación diagonal para b
½ y Hb:
¡
X
1
¤ =
k
j
w j ln (w j ) + ¯
X
j
w jE j + ¸
X
j
w j;
cuya variación frente a cambios de la probabilidades ± w j debe anularse
X
±¤ = ¡ k
± w j (ln (w j ) + ¯ E j + ¸ + 1 ) = 0 ;
j
59
(4.57)
(4.58)
se obtiene
w j = ex p [¡ (¯ E j + ¸ + 1 )];
(4.59)
P
como en el caso clásico. La normalización j w j = 1 y la identificación del multiplicador de Lagrange ¯ con 1 = k T , siguiendo los argumentos del capítulo 2, I parte,
permite reconocer que las probabilidades w j corresponden al ensemble canónico. La
entropía de esta distribución de probabilidades es un máximo.
4.6.4 Principio extremal del operador estadístico del ensemble gran canónico.
En este caso los vínculos para el cálculo del extremo de la entropía son la energía
media, el número medio de partículas y la normalización de la matriz densidad. El
operador estad́istico del ensemble gran canónico es aquel que corresponde al máximo
de la entropía por sobre cualquier otro, sujeto a las condiciones mencionadas. Como
ya se dijo (ecuación 4.18) en equilibrio los operadores Hb y Nb conmutan y tienen
autofunciones comunes. En fórmulas, los vínculos son
hH i = Tr [b
½ Hb];
hN i = Tr [b
½ Nb];
Tr [b
½] = 1:
(4.60)
La funcional cuyo extremo hay que calcular se puede escribir como
© = Tr [b
½ ln (b
½ )] + ¯ Tr [b
½ Hb] ¡ º Tr [b
½ Nb] + ¸ Tr [b
½ ]:
Variando el operador estadístico en ±b
½ , ponemos ± © = 0 y obtenemos
n h
io
¡ Tr ±b
½ ln (b
½ ) + (¸ + 1 ) + ¯ Hb ¡ º Nb = 0 :
(4.61)
(4.62)
Esta ecuacíon debe valer para cualquier ±b
½ de manera que escribiendo º = ¯ ¹ , resulta
h ³
´i
b
½ = C ex p ¡ ¯ Hb ¡ ¹ Nb ;
(4.63)
donde C = ex p [¡ (¸ + 1 )]. A posteriori, mediante los argumentos termodinámicos
del capítulo 5, I parte, se reconoce que ¹ es el potencial químico. Dado que Tr [b
½]= 1
podemos determinar el valor de la constante y escribir
n h
³
´io
n
h ³
´io
e
b
b
e
b
b
b
½ = ex p ¯ − ¡ H ¡ ¹ N
; ex p (¡ ¯ − ) ´ Tr ex p ¡ ¯ H ¡ ¹ N
; (4.64)
donde hemos introducido el gran potencial −e.
Propiedades extremales de los ensembles de equilibrio en la formulación cuántica
60
b b
son
h las³autofunciones
´i comunes a H y N entonces son también autofunciones de ex p ¡ ¯ Hb ¡ ¹ Nb , el cual actúa sobre ª k ;N de la forma
Si ª
k ;N
h ³
´i
ex p ¡ ¯ Hb ¡ ¹ Nb ª
k ;N
= ex p [¡ ¯ (E
k
¡ ¹ N )]ª
k ;N
:
(4.65)
Por lo tanto
ex p (¡ ¯ −e) =
=
n
h ³
´io
Tr ex p ¡ ¯ Hb ¡ ¹ Nb
=
Z
h ³
´i
X
ª ¤k ;N (x ) ex p ¡ ¯ Hb ¡ ¹ Nb ª
k ;N
(x ) d x
(4.66)
k ;N
y se obtiene la fórmula para el gran potencial que hemos empleado en la primera
parte (capítulo 5) de estas notas
)
(
X
ex p [¡ ¯ (E k ¡ ¹ N )] :
(4.67)
−e = ¡ k T ln
k ;N
La diagonalización simultánea de b
½ ; Hb; Nb en el equilibrio permite que los valores
medios se puedan calcular sin emplear los operadores cuánticos, tal como hemos
hecho en la primera parte. Se puede demostrar que S = ¡ k Tr [b
½ ln (b
½ )] es un máximo
para el operador estadístico gran canónico.