ANTIDERIVADAS

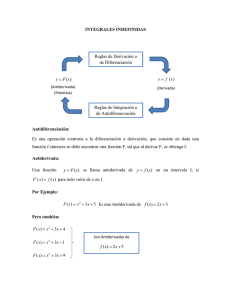
UNIVERSIDAD ANTONIO NARIÑO
GUIA 1
ANTIDERIVADAS
OBJETIVO:
Aprender el concepto de antiderivada e integral indefinida y
resolver integrales usando las formulas básicas.
Concepto:
Dada una función, sabemos como hallar su derivada, este problema
lo estudia el cálculo diferencial. Cuando se conoce la derivada de
una función y se desea conocer la función original, se usa el cálculo
integral.
La antiderivada o primitiva de una funcion f(x)
es otra función F(x)+C
donde C es una constante. Si al derivar F(x)+C nos da como respuesta f(x)
Es decir F’(x) = f(x)
A la funcion F(x) se le llama una antiderivada de la una funcion f(x).
Ejemplo ¿Qué se derivo para que la derivada sea f ' ( x ) = 4 ?
Por el método de Ensayo y Error se puede ver que la funcion que se
derivo es:
F1 (x)=
4x
pero también las funciones
F (x)=4x+5
F (x)=4x-2
F (x)=4x-12
F (x)=4x+15
F (x)=4x+8
F(x) = 4x+C
2
3
4
5
6
Es decir que la funcion cuya derivada es 4 es una familia de
funciones en este caso lineales cuyos miembros todos tienen
pendiente de +4 pero diferentes intersecciones con el eje y como
vemos en las graficas para los diferentes valores de la constante C
C =0 C=5 C=-2 C=12 C=15 C=8
Se puede afirmar que la funcion F(x)=4x+C es la antiderivada de f(x)=4
2 EJEMPLO
Hallar la antiderivada de f ( x) = 3x 2
La funcion que se derivó es F(x)= x 3 pero también
x +5
F (x)= x +9
F (x)= x -2
3
F (x)= x +
2
F(x)= x +C
F1 (x)=
3
3
2
3
3
3
4
3
Pues todas tienen pendientes 3x es decir se puede afirmar que
la funcion F(x)= x3 +C es la antiderivada de f ( x) = 3x con
2
2
diferentes intersecciones con el eje y como vemos en las graficas
para los diferentes valores de la constante C
C =5 C=9 C=-2 C=3/2
INTEGRALES INDEFINIDAS
INTEGRACION
Al proceso de hallar las antiderivadas se le llama integración y a la familia de
funciones que se obtiene mediante este proceso se llama integrales indefinidas
y se representa mediante los símbolos
∫
o signo de la integral ,
dx indica la variable respecto a la cual se lleva el proceso de integración
los símbolos siguientes siempre van juntos
y en el cuadro va la funcion f(x) que se debe integrar así:
∫
f ( x ) dx
donde f(x) es la derivada de la funcion desconocida llamada integrando
y la respuesta es una familia de funciones así
∫
f ( x ) dx = F ( x ) + C
A la constante C se le llama constante de integración
Por lo tanto en los 2 ejemplos anteriores la antiderivada de
se escribe mediante una integral indefinida así:
f ( x) = 4
∫ 4dx = 4 x + C
y la antiderivada de
f ( x) = 3 x 2 se escribe
2
3
3
x
dx
=
x
+c
∫
REGLAS BASICAS DE INTEGRACION
A continuación se presenta un conjunto de reglas para encontrar la integral
indefinida de una funcion
1- INTEGRAL DE UNA FUNCION CONSTANTE
F(x)=K donde k es un numero real
∫
kdx
= kx + C
EJEMPLOS
∫ − 9dx = −9 x + C
1
1
dx
=
x+C
2- ∫
8
8
3- ∫ πdx = πx + C
1-
∫ 52dx = 52 x + C
5- ∫ m dx = m x + C
4-
2- INTEGRAL DE UNA POTENCIA
n
f ( x) = x
∫
x
n
dx
x n +1
=
+ C
n + 1
n ≠ − 1
con
Cuando el integrando es x elevado a algún exponente real se aumenta el
exponente de x en 1 ,se divide en el nuevo exponente y se suma la constante
de integración
EJEMPLOS
1-
∫
2-
∫
3-
∫
x5
x dx =
+c
5
x −6
−7
x dx =
+c
−6
4
3
2
x dx =
5
2
x
+c
5
2
es decir después de efectuar el producto de
medios y extremos resulta así:
4-
∫
x
−7
3
dx =
− 3x
4
−4
3
∫
3
2
x dx =
+c
2x
5
5
2
+c
5
∫
x dx =
∫
1
2
3
2 2
x dx =
x +c
3
cada vez que aparece una integral con radical, se vuelve a reescribir la
integral con el radical en forma de potencia fraccionaria como en el último
ejemplo
Cuando la potencia esta en el denominador se reescribe subiendo la potencia
con exponente negativo
1
dx
n
x
∫
=
∫
x
− n
dx
EJEMPLOS
1-
2-
2-
x −8
1
−9
∫ x 9 dx = ∫ x dx = − 8 + c
1
x −42
− 43
∫ x 43 dx = ∫ x dx = − 42 + c
∫
1
x
2
17
dx =
∫x
2
−
17
x
dx =
−
3- INTEGRAL DE UNA
POTENCIA
−
15
17
15
17
+c=
− 17
15
x
− 15
17
+C
CONSTANTE MULTIPLICADA POR
xn + 1
n
n
+C
∫ kx dx = k ∫ x dx = k
n +1
n ≠ −1
Las constantes salen de la integral y multiplican por las potencias
UNA
EJEMPLOS
5
x
5
10
x
dx
=
10
+
c
=
2
x
+c
1- ∫
5
10
x
− 7 10
9
−
7
x
dx
=
−
7
+
c
=
x
2- ∫
10
10
5 − 12
5 x − 11
x dx =
+c
3- ∫ 8
8 ( − 11 )
4
4-
∫
6
5
5x
2 x dx = 2
11
11
5
10
+c =
x
11
11
5
+c
INTEGRAL DE UNA SUMA O RESTA DE FUNCIONES
Se integra cada sumando es decir se distribuye el símbolo de la integral y se
suma una sola constante C
∫ [ f ( x ) ± g ( x ) ]dx = ∫
f ( x ) dx ±
∫ g ( x ) dx
EJEMPLOS
1-
∫ (8 + 3 x + x
3
− 2 x − 6 ) dx = ∫ 8 dx + ∫ 3 xdx + ∫ x 3 dx − ∫ 2 x − 6 dx
Por lo tanto integrando cada termino se tiene :
3 x 2 x 4 2 x −5
+
+
+C
8x +
2
4
5
INTEGRAL DE LA POTENCI A n=-1
1
con n = −1
x
f ( x ) = x −1
f ( x) =
O
∫
1
dx
x
= ln
x
+ C
INTEGRAL DE LA FUNCION EXPONENCIAL (BASE E)
Es la misma funcion exponencial
∫
e
x
=
dx
EJERCICIOS
BASICAS
e
x
+
RESUELTOS
2
3
1- ∫ (6 x + 5x
c
APLICANDO
LAS
REGLAS
− 8)(4 x5 − 3x)dx
primero se efectúa el producto
indicado y se obtiene la integral de una suma de constantes por potencias
7
8
5
4
3
∫ (24 x + 20 x − 32x − 18 x − 15 x + 24 x) dx
se reducen términos semejantes si los hay y después se integra cada termino
aplicando las formulas básicas de integración en este caso suma de constantes
por potencias
24 x9 + 20 x8 − 32 x6 − 18 x5 − 15 x4 + 24 x2 + C
5
9
8
6
4
2
Simplificando se obtiene:
24x9 + 5 x8 −16x6 −18x5 −15x4 +12x2 +C
5
9
2
3
4
--------------------------------------------------------------------------5
2
2- ∫ (4x + 7) dx se desarrolla el binomio indicado
10
5
∫ (16x + 56x + 49)dx
Ahora se integra cada término y se obtiene:
16 11 56 6
x +
x + 49 x + C
11
6
--------------------------------------------------------------3
5
3se
cambia el radical por
∫ 5 ( 4 x + 7 ) dx
x
fraccionaria y luego se sube la potencia y se efectúa el producto
∫
∫
potencia
−1
3x 5 (4x5 + 7)dx
24
−1
(12 x 5 +21x 5 )dx
5
(12 ) x
29
60
x
29
29
5
29
5
Se integra cada término
4
5
+ ( 21) x 5 + C Simplificando
4
4
105 5
+
x +C
4
ACTIVIDAD I
MATEMATICAS II
INTEGRAL INDEFINIDA
OBJETIVOS
1. Afianzar el concepto de integral indefinida resolviendo integrales.
2. Aplicar las formulas básicas de integración después de resolver operaciones algebraicas
Actividades.
1) Halle la antiderivada de las siguientes funciones
4
−
5
−1
7
c) 8 x
d)123 x e) 5 x 3
a) x
b)
x
2) Calcule las siguientes integrales indefinidas –
1
2-
∫ (x
−3
x2 + 2
dx
x +1
1
∫
4-
∫x
678-
3 4
x )dx
4
x 4 + 53 x − 3 x x − 2
dx
∫
4x
3-
5-
+
x2 + 2
2
dx
∫ (1 + x + 1 − x )dx
x 4 + 5 3 x − 3x x − 2
dx
∫
4x
e
x
∫ x + e dx
(
)
x2 − x
∫ (x − 1)2 dx
(1 + x )3 dx
9-
∫
10-
∫ (x − x )
x
−3
x x x dx