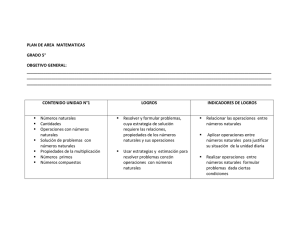
MateMáticas1 - Ediciones Castillo

Luis Fernando Ojeda ánimas
C a r l o s M a r t í n e z L ARA
A
p r a c t i c a r
C
IO
N
elia ibeth manjarrez córdova
1
O
t r a b a j o
PR
d e
M
AT
ER
IA
L
D
E
C u a d e r n o
M
O
Matemáticas
SACMA1WB_B0.indd 1
30/01/13 10:41
C
IO
N
Dirección editorial Adriana Beltrán Fernández • Subdirección editorial Tania Carreño
King • Gerencia de Secundaria Aurora Saavedra Solá • Gerencia de diseño Renato Aranda
• Edición Javier Jiménez Alba, René López Villamar, José Antonio Gaytán García, Milosh
Trnka Rodríguez • Asistencia editorial Alma Rosa Valadez Canseco, Ricardo Medel Esquivel,
Victor Duarte Alaniz • Revisión técnica Dalibor Trnka Rodríguez, Najla Amira Ochoa Leonor •
Corrección de estilo María del Carmen Solano • Diseño de la serie Renato Aranda y Gustavo
Hernández Jaime • Supervisión y Coordinación de Diseño Gabriela Rodríguez • Formación
Capitulares • Supervisión y Coordinación de imagen Tere Leyva Nava • Gráficos y Esquemas
Mariana Jiménez, Carlos Zariñana • Digitalización y retoque Juan Ortega • Ilustración
Horacio Sierra • Gerencia de producción Alma Orozco • Coordinación de producción
Alma Ramírez
O
Primera edición: diciembre de 2012
D
E
Insurgentes Sur 1886, Col. Florida,
Del. Álvaro Obregón,
C.P. 01030, México, D. F.
Tel.: (55) 5128-1350
Fax: (55) 5128-1350 ext. 2899
PR
Todos los derechos reservados.
D. R. © 2012, Ediciones Castillo, S. A. de C. V.
Castillo ® es una marca registrada
O
M
A practicar Matemáticas 1, Guía para el Maestro
L
Ediciones Castillo forma parte del Grupo Macmillan
ER
IA
www.grupomacmillan.com
www.edicionescastillo.com
[email protected]
Lada sin costo: 01 800 536 1777
AT
Miembro de la Cámara Nacional
de la Industria Editorial Mexicana
Registro núm. 3304
M
ISBN de la serie: 978-607-463-780-9
Prohibida la reproducción o transmisión parcial o total de esta obra por cualquier medio
o método o en cualquier forma electrónica o mecánica, incluso fotocopia, o sistema para
recuperar información, sin permiso escrito del editor.
Impreso en México/Printed in Mexico
SACMA1TG1E13_L.indd 1
30/01/13 17:42
Presentación
M
AT
ER
IA
L
D
E
PR
O
M
O
C
IO
N
“Las matemáticas no me gustan”, “Las matemáticas son difíciles”,
“Las matemáticas son aburridas”, “Siempre repruebo matemáticas”… ¡Alto!... Calma… deja de ver a las matemáticas como tu enemigo más acérrimo (aunque a muchas personas sí les agradan). Esta
materia debe convertirse en tu aliado para resolver problemas. Lo
único que tendrás que hacer es familiarizarte con su metodología,
las fórmulas y ecuaciones que te permitirán descubrir las claves
para resolver, no sólo los “casos” que se presenten en este libro, sino
problemas de tu vida cotidiana.
Cada vez que nos enfrentamos a un reto es posible que experimentemos rechazo o temor (y más si has fallado constantemente),
pero el temor es una palabra que no debe existir en tu diccionario. No dejes de intentarlo, dicen por ahí que “La práctica hace al
maestro” y cuando realices los ejercicios que aquí se presentan, te
sorprenderá lo fácil que es resolver problemas cotidianos aplicando
matemáticas.
Todos tenemos diferentes estilos al aprender, por eso procuramos
que en este libro exista variedad de problemas, de situaciones y de
métodos de solución. En cada lección te ofrecemos los elementos
necesarios para ir, paso a paso, de lo más fácil a lo más complicado.
Así también te brindamos consejos que te pondrán alerta para evitar errores. No dudes, sólo es cuestión de práctica, sin embargo no
te confíes y no dejes el estudio para un día antes del examen.
No desconfíes de las matemáticas, confía en tus habilidades, despierta tu curiosidad y atrévete a mirar esta materia desde un punto
de vista distinto, es como las obras de arte moderno, para encontrar
su belleza, hay que mirarlas desde “otro ángulo”. Las matemáticas
forman parte de tu vida, no las dejes encerradas en la escuela. Te
aseguramos que con la práctica, llegarás a dominarlas. ¡Adelante!
3
SACMA1WB_B0.indd 3
30/01/13 10:41
3 Presentación
6 Conoce tu libro
7Dosificación
9 BLOQUE 1
Conversión de fracciones a notación
decimal y viceversa
14Representación de números fraccionarios
y decimales en la recta numérica
17 Problemas que implican más de una
operación de suma y resta de fracciones
21Sucesiones de números y de figuras
25Significado de fórmulas geométricas
28Trazo de triángulos y cuadriláteros mediante
el uso del juego de geometría
32 Propiedades de las rectas notables
del triángulo
35 Problemas de reparto proporcional
39Juegos de azar y elección de estrategias
43Evaluación
E
PR
O
M
O
C
IO
N
10
D
45 BLOQUE 2
M
AT
ER
IA
L
46
Criterios de divisibilidad entre 2, 3 y 5.
Números primos y compuestos
49Máximo común divisor y mínimo común
múltiplo
53 Problemas aditivos con fracciones
y decimales
57Multiplicación y división con números
fraccionarios
61 Propiedades de la mediatriz y la bisectriz
65 Fórmulas de perímetro y área de polígonos
regulares
68 Proporcionalidad directa
71Evaluación
Índice
4
SACMA1WB_B0.indd 4
30/01/13 10:41
73 BLOQUE 3
C
IO
N
74Multiplicación de números decimales
78División de números decimales
82Ecuaciones de primer grado
86 Construcción de polígonos regulares
89El perímetro y el área de polígonos regulares
92 Factores constantes de proporcionalidad
96Experiencia aleatoria
99Tablas de frecuencia absoluta y relativa
103Evaluación
M
O
105BLOQUE 4
M
AT
ER
IA
L
D
E
PR
O
1 06Números positivos y negativos
110 Construcción de círculos
114 La longitud de la circunferencia y el área
del círculo
118Regla de tres simple directa
122Efectos del factor inverso en una relación
de proporcionalidad
125 Problemas de conteo
129 Lectura y comunicación de información
representada en gráficas de barras
y circulares
133Evaluación
135BLOQUE 5
1 36Suma y resta de números enteros
140Notación científica
144 Potencia y raíz cuadrada
147 Progresión aritmética
150 Perímetro y área del círculo
154 Problemas de proporcionalidad múltiple
157Evaluación
159Bibliografía
5
SACMA1WB_B0.indd 5
30/01/13 10:41
Entrada de bloque
Este libro está organizado en fichas
de trabajo, en las que practicarás
y ejercitarás los contenidos y
aprendizajes que desarrollaste en
tus clases. Al inicio de cada bloque
se muestran los ejes, temas y
aprendizajes que trabajarás en cada
ficha.
BLOQUE 3
Eje
Tema
1
Problemas
multiplicativos
Sentido numérico
y pensamiento
algebraico
2
Contenido
• Resolución de problemas que impliquen la multiplicación
de números decimales en distintos contextos, utilizando el
algoritmo convencional.
• Resolución de problemas que impliquen la división de números
decimales en distintos contextos, utilizando el algoritmo
convencional.
• Resolución de problemas que impliquen el planteamiento y la
resolución de ecuaciones de primer grado de la forma x + a = b;
ax = b; ax + b = c, utilizando las propiedades de la igualdad, con
a, b y c números naturales, decimales o fraccionarios.
3
Patrones y
ecuaciones
4
Figuras y cuerpos
• Construcción de polígonos regulares a partir de distintas
informaciones (medida de un lado, del ángulo interno, ángulo
central). Análisis de la relación entre los elementos de la
circunferencia y el polígono inscrito en ella.
Medida
• Resolución de problemas que impliquen calcular el perímetro y
el área de polígonos regulares.
Forma, espacio y
medida
5
6
Manejo de la
información
7
Proporcionalidad
y funciones
• Formulación de explicaciones sobre el efecto de la aplicación
sucesiva de factores constantes de proporcionalidad en
situaciones dadas.
Nociones de
probabilidad
• Anticipación de resultados de una experiencia aleatoria, su
verificación al realizar el experimento y su registro en una tabla
de frecuencias.
Análisis y
representación de
datos
8
• Lectura y comunicación de información mediante el uso de
tablas de frecuencia absoluta y relativa.
Desafío matemático
b) ¿Qué expresión representa una fórmula para calcular el perímetro de
la cancha de futbol?
4l = 128
4a = 128
l + a = 128
2l + 2a = 128
c) ¿Con qué expresión se calcula el perímetro de la cancha de futbol?
(a + 20) + (a + 20) + a + a = 128
a + a + a + a = 128
(a + 20) + a + a + a = 128
(a − 20) + (a − 20) + a + a = 128
MANEJO
MANEJO DE LA INFORMACIÓN
INFORMACIÓN
IO
FORMA, ESPACIO Y MEDIDA
1. Selecciona la respuesta correcta.
a) ¿Cuál de las siguientes expresiones representa que el largo de la cancha de futbol sea 20 m mayor que su ancho?
l = a × 20
l = a − 20
l = a ÷ 20
l = a + 20
Ahora practica
1. La entrada al cine Maxinépolis cuesta $25.50. ¿Cuántas personas ingresaron al cine en una función, si en total se recaudaron $2 142.00? Escribe una expresión algebraica para representar el problema y resuélvelo.
C
Una forma de resolver
problemas que requieren el planteamiento de
ecuaciones con una sola
incógnita es seguir estos
pasos:
1. Leer el problema con
atención hasta entenderlo.
2. Representar algebraicamente el problema
con una ecuación. La
cantidad desconocida
se representa con una
literal.
3. Si hay más de una
incognita, escribir, de
acuerdo con los datos
del problema, una de
ellas en términos de
la otra.
4. Escribir la ecuación
en términos de una
variable.
5. Encontrar el valor de
la incógnita mediante las propiedades de
la igualdad. A esto
se le llama resolver
la ecuación.
6. Una vez resuelta la
ecuación, comprobar
que la solución cumple las condiciones
iniciales del problema.
1. ¿Cuáles son las dimensiones de una cancha rectangular de futbol rápido
si su largo es 20 m mayor que su ancho, y su perímetro es de 128 m?
Ahora practica
Esta sección contiene diversos problemas y
ejercicios con los que pondrás en práctica las
habilidades y conocimientos que adquiriste
en tus clases. Son problemas diversos que
aumentan de complejidad de manera gradual,
esto te ayudará a mejorar tus competencias
matemáticas.
2. En dos cubetas de distinto tamaño se dividieron 18.93 litros de agua. Si
en la cubeta más grande había x litros de agua, ¿cuántos litros había en
la cubeta más chica? Escribe la expresión algebraica correspondiente.
82
O
Contenido: Resolución de problemas que impliquen el planteamiento y la resolución de ecuaciones de primer grado de la
forma x + a = b; ax = b; ax + b = c, utilizando las propiedades de la igualdad, con a, b y c números naturales, decimales o
fraccionarios.
PR
Regreso al Desafío matemático
Al final de cada ficha se presenta un espacio
para replantear el problema inicial que ya
resolviste. Es una oportunidad para revisar,
evaluar y mejorar tus conocimientos y
estrategias de solución.
9. Anota los números sobre los vértices de la estrella de
forma que la suma de los tres números en cada segmento de recta sea igual a 0.
−2
−3
SENTIDO NUMÉRICO Y
PENSAMIENTO ALGEBRAICO
0
−5
6
−8
10
7
−9
−6
Regreso al Desafío matemático
FORMA, ESPACIO Y MEDIDA
Conceptos clave
E
1. Regresa al Desafío matemático y, con base en lo que has practicado,
revisa si tu respuesta es correcta; corrígela si es necesario.
2. Inventa un problema que implique una deuda o saldo a favor en una
cuenta bancaria y se resuelva con una resta donde el minuendo y el
sustraendo sean números negativos.
Para restar dos números
enteros al minuendo se
suma él número opuesto
del sustraendo. Así, una
resta se resuelve mediante una suma.
Ejemplos:
(+9) − (−5)
= (+9) + (+5)
= +14
(−15) − (−7)
= (−15) + (+7)
= −8
D
Validación
1. Completa los párrafos.
La operación para calcular cuánto dinero le queda a
Miguel después del segundo movimiento bancario es
.
Así se obtiene una
de números con signo
.
(+10521) + (−11984) =
(+10521) – (+11984) =
Para encontrar el resultado del último movimiento
de números con signo
hay que hacer una
.
Para encontrar el resultado del tercer movimiento
bancario se hace una
L
−2692 + (+3881) =
de números con signo
Se señala el eje al que corresponde la ficha
que estás trabajando.
Conceptos clave
Para resolver los problemas que se
plantean necesitas tener bien claros los
conceptos a los que se refieren. Esta
sección incluye la definición de esos
conceptos apoyada con ejemplos claros.
MANEJO
MANEJO DE LA INFORMACIÓN
INFORMACIÓN
Validación
Procedimiento
M
O
SENTIDO NUMÉRICO Y
PENSAMIENTO ALGEBRAICO
Desafío matemático
Las claves del problema
Las claves del problema
En esta sección se explican algoritmos y
métodos para resolver diversos problemas.
Incluye ejemplos para apoyar su comprensión.
Una de las grandes aportaciones del álgebra es el uso de “literales” para expresar “cantidades
desconocidas”. Así, un problema cotidiano puede traducirse al lenguaje algebraico en una
expresión simbólica y resolverse haciendo uso de las propiedades de la igualdad y de los
algoritmos convencionales de las operaciones básicas.
En todo problema hay elementos clave que
debes reconocer y que son fundamentales
para resolver la situación. En esta sección te
ayudamos a descubrirlos.
¿Tu solución al desafío matemático fue
acertada? Valida tu resultado completando el
procedimiento que te presentamos.
Procedimiento
Ecuaciones de primer grado
El trabajo por competencias implica la solución
de situaciones problemáticas. Al inicio de
cada ficha encontrarás un problema que
deberás resolver a partir de las habilidades y
conocimientos que has desarrollado en tu
curso de Matemáticas. Es un desafío, y los
desafíos, hay que enfrentarlos.
N
Ficha
.
(−1463) – (−1229) =
La cantidad final que Miguel tiene en su cuenta de
crédito es
.
139
7. 2
O
A'
C
4.8 cm
A
B
a) Describe un procedimiento para obtener las medidas del triángulo original.
En el ejemplo, las distancias entre los puntos OA,
OB y OC, tienen la misma
longitud.
b) ¿Cuáles son las medidas de los lados del triángulo original?
A
3. Las siguientes figuras geométricas están a escala. Calcula las medidas
de los lados de las figuras originales y trázalas a partir de las medidas
que calculaste.
a)
D
Escala 3:5
c) ¿Los dos puntos que trazaste coinciden?
A'
M
Validación
Para saber si es posible construir el balneario de modo
que se localice a la misma distancia de los cuatro
poblados, primero se unen dos de ellos; por ejemplo, A y
, y se traza su
Ejemplo:
El siguiente dibujo está
a escala
1 .
150
2.54 cm
La altura del árbol original se calcula, entonces,
así:
C
B
2. Explica cuál sería un buen lugar para ubicar el balneario. Justifica tu respuesta.
B, mediante un
El factor de escala
inverso es el número
por el cual se multiplica
la figura a escala para
obtener las medidas de
la figura original. Si el
factor de escala es
a , el factor
b
b
.
inverso es
a
2. Una maqueta está a escala 1:25. Si el largo de un muro en la maqueta
es de 10 cm, ¿cuántos metros mide el muro original?
1. Lee nuevamente el Desafío matemático y haz sobre la figura los trazos que se piden.
a) Localiza el punto que se localiza a la misma distancia de los puntos A, B y C.
b) Localiza el punto que se encuentra a la misma
distancia de los puntos C, B y D.
.
Después se unen otros dos poblados, por ejemplo,
y
su
, mediante otro
, y se traza
b)
.
Escala 3:1
Finalmente, se analiza si las tres rectas notables, es decir, si las
,
coinciden en un solo punto:
• Si coinciden, es en ese punto donde se debe construir el balneario, porque se
localiza
de los cuatro poblados.
• Si no es así, significa que no es posible construir el balneario que cumpla esa
condición.
64
cm
C
10. A partir de tu respuesta a la pregunta anterior
determina un método para localizar el centro de la siguiente circunferencia. Explica el
procedimiento.
Regreso al Desafío matemático
MANEJO
MANEJO DE LA INFORMACIÓN
INFORMACIÓN
4
cm
B
Procedimiento
1. El triángulo A’ se obtuvo al multiplicar las medidas del triángulo original
A por un factor de escala igual a 3 .
3.6
SENTIDO NUMÉRICO Y
PENSAMIENTO ALGEBRAICO
FORMA, ESPACIO Y MEDIDA
El punto de intersección
de dos mediatrices de
dos segmentos consecutivos es equidistante de
los extremos de dichos
segmentos.
mediatrices
B'
De nuevo se unen otros dos
poblados diferentes a los
anteriores; por ejemplo,
y
2.54 cm ×
= 2.81 m.
Error frecuente
En ocasiones se confunde el factor de escala
inverso con el factor
de escala y se usa para
calcular las medidas de
la imagen original.
Por ejemplo, al calcular el largo del fuselaje
del avión a partir de la
medida en un modelo a
escala de 1:50, se puede
cometer el error de
multiplicar la medida del
largo del fuselaje en el
modelo, que es de
12.45 cm, por el factor
1
, cuando lo correcto
50
es multiplicar 12.45 cm
, mediante otro
, y se traza su
Contenido: Resolución de problemas geométricos que impliquen el uso de las propiedades de la mediatriz
de un segmento y la bisectriz de un ángulo.
150
= 381 cm
1
.
por
50
.
1
Contenido: Análisis de los efectos del factor inverso en una relación de proporcionalidad, en particular en una
reproducción a escala.
123
MANEJO DE LA INFORMACIÓN
AT
Ahora practica
Observación
FORMA, ESPACIO Y MEDIDA
Hay conceptos o situaciones
en las que debes poner especial
atención. En esta sección los
resaltamos para que no pasen
desapercibidos.
A
9. Determina el punto Q que se encuentra a la
misma distancia de los puntos A, B y C. ¿Se
puede trazar una circunferencia con centro
en Q que pase por los otros tres puntos? Justifica tu respuesta.
ER
Observación
SENTIDO NUMÉRICO Y
PENSAMIENTO ALGEBRAICO
IA
Contenido: Resolución de problemas que implican el uso de sumas y restas de números enteros.
Error frecuente
En los procedimientos
matemáticos es común cometer
errores o equivocaciones. En esta
sección te mostramos los más
comunes.
Conoce tu libro
6
SACMA1WB_B0.indd 6
30/01/13 10:41
2y3
Conversión de fracciones decimales y no decimales a su escritura decimal
y viceversa.
10 a 13
Representación de números fraccionarios y decimales en la recta
numérica a partir de distintas informaciones, analizando las convenciones
de esta representación.
14 a 16
Resolución y planteamiento de problemas que impliquen más de una
operación de suma y resta de fracciones.
17 a 20
4. Sucesiones de números y
de figuras.
Construcción de sucesiones de números o de figuras a partir de una regla
dada en lenguaje común. Formulación en lenguaje común de expresiones
generales que definen las reglas de sucesiones con progresión aritmética
o geométrica, de números y de figuras.
21 a 24
5
5. Significado de fórmulas
geométricas.
Explicación del significado de fórmulas geométricas, al considerar las
literales como números generales con los que es posible operar.
25 a 27
Trazo de triángulos y cuadriláteros mediante el uso del juego de
geometría
28 a 31
Trazo y análisis de las propiedades de las alturas, medianas, mediatrices y
bisectrices en un triángulo.
32 a 34
Resolución de problemas de reparto proporcional.
35 a 38
Identificación y práctica de juegos de azar sencillos y registro de los
resultados. Elección de estrategias en función del análisis de resultados
posibles.
39 a 42
Formulación de los criterios de divisibilidad entre 2, 3 y 5. Distinción entre
números primos y compuestos.
46 a 48
Resolución de problemas que impliquen el cálculo del máximo común
divisor y el mínimo común múltiplo.
49 a 52
9 y 10
10 y 11
9. Juegos de azar y elección
de estrategias.
1. Criterios de divisibilidad
entre 2, 3 y 5. Números
primos y compuestos.
2. Máximo común divisor y
mínimo común múltiplo.
M
O
O
PR
8y9
E
7y8
D
6y7
6. Trazo de triángulos y
cuadriláteros mediante
el uso del juego de
geometría.
7. Propiedades de las rectas
notables del triángulo
8. Problemas de reparto
proporcional.
C
4
6
3. Problemas aditivos con
fracciones y decimales.
Resolución de problemas aditivos en los que se combinan números
fraccionarios y decimales en distintos contextos, empleando los
algoritmos convencionales.
53 a 56
12 y 13
4. Multiplicación y
división con números
fraccionarios.
Resolución de problemas que impliquen la multiplicación y división con
números fraccionarios en distintos contextos, utilizando los algoritmos
usuales.
57 a 60
13 y 14
5. Propiedades de la
mediatriz y la bisectriz.
Resolución de problemas geométricos que impliquen el uso de las
propiedades de la mediatriz de un segmento y la bisectriz de un ángulo.
61 a 64
ER
IA
11 y 12
AT
Bloque 2
2. Representación de
números fraccionarios
y decimales en la recta
numérica.
3. Problemas que implican
más de una operación de
suma y resta de fracciones
Páginas
L
Bloque 1
3y4
1. Conversión de fracciones
a notación decimal y
viceversa.
Contenido
N
1y2
Ficha
IO
Semanas
6. Fórmulas de perímetro
y área de polígonos
regulares.
Justificación de las fórmulas de perímetro y área de polígonos regulares,
con apoyo de la construcción y transformación de figuras.
65 a 67
15 y 16
7. Proporcionalidad directa.
Identificación y resolución de situaciones de proporcionalidad directa
del tipo “valor faltante” en diversos contextos, con factores constantes
fraccionarios.
68 a 70
M
14 y 15
Dosificación
7
SACMA1WB_B0.indd 7
30/01/13 10:41
Resolución de problemas que impliquen la multiplicación de números
decimales en distintos contextos, utilizando el algoritmo convencional.
74 a 77
17 y 18
2. División de números
decimales.
Resolución de problemas que impliquen la división de números decimales
en distintos contextos, utilizando el algoritmo convencional.
78 a 81
18 y 19
3. Ecuaciones de primer
grado.
Resolución de problemas que impliquen el planteamiento y la resolución
de ecuaciones de primer grado de la forma x + a = b; ax = b; ax + b = c,
utilizando las propiedades de la igualdad, con a, b y c números naturales,
decimales o fraccionarios.
82 a 85
4. Construcción de
polígonos regulares.
Construcción de polígonos regulares a partir de distintas informaciones
(medida de un lado, del ángulo interno, ángulo central). Análisis de la
relación entre los elementos de la circunferencia y el polígono inscrito en
ella.
86 a 88
20 y 21
5. El perímetro y el área de
polígonos regulares.
Resolución de problemas que impliquen calcular el perímetro y el área de
polígonos regulares.
89 a 91
21 y 22
6. Factores constantes de
proporcionalidad.
Formulación de explicaciones sobre el efecto de la aplicación sucesiva de
factores constantes de proporcionalidad en situaciones dadas.
92 a 95
22 y 23
7. Experiencia aleatoria.
Anticipación de resultados de una experiencia aleatoria, su verificación al
realizar el experimento y su registro en una tabla de frecuencias.
96 a 98
23 y 24
8. Tablas de frecuencia
absoluta y relativa.
Lectura y comunicación de información mediante el uso de tablas de
frecuencia absoluta y relativa.
99 a 102
24 y 25
1. Números positivos y
negativos.
Planteamiento y resolución de problemas que impliquen la utilización de
números enteros, fraccionarios o decimales positivos y negativos.
106 a 109
25 y 26
2. Construcción de círculos.
Construcción de círculos a partir de diferentes datos (el radio, una cuerda,
tres puntos no alineados, etc.) o que cumplan condiciones dadas.
26 y 27
3. La longitud de la
Justificación de la fórmula para calcular la longitud de la circunferencia y
circunferencia y el área del el área del círculo (gráfica y algebraicamente). Explicitación del número p
(pi) como la razón entre la longitud de la circunferencia y el diámetro.
círculo.
114 a 117
27 y 28
4. Regla de tres simple
directa.
Análisis de la regla de tres, empleando valores enteros o fraccionarios.
118 a 121
28 y 29
5. Efectos del factor inverso
en una relación de
proporcionalidad.
Análisis de los efectos del factor inverso en una relación de
proporcionalidad, en particular en una reproducción a escala.
122 a 124
29 y 30
6. Problemas de conteo.
Resolución de problemas de conteo mediante diversos procedimientos.
Búsqueda de recursos para verificar los resultados.
125 a 128
30 y 31
7. Lectura y comunicación
de información
representada en gráficas
de barras y circulares.
Lectura de información representada en gráficas de barras y circulares,
provenientes de diarios o revistas y de otras fuentes. Comunicación de
información proveniente de estudios sencillos, eligiendo la representación
gráfica más adecuada.
129 a 132
1. Suma y resta de números
enteros.
Resolución de problemas que implican el uso de sumas y restas de
números enteros.
136 a 139
IO
C
M
O
O
PR
E
D
L
110 a 113
2. Notación científica.
Uso de la notación científica para realizar cálculos en los que intervienen
cantidades muy grandes o muy pequeñas.
140 a 143
33 y 34
3. Potencia y raíz cuadrada.
Resolución de problemas que impliquen el cálculo de la raíz cuadrada
(diferentes métodos) y la potencia de exponente natural de números
naturales y decimales.
144 a 146
34 y 35
4. Progresión aritmética.
Obtención de la regla general (en lenguaje algebraico) de una sucesión
con progresión aritmética.
147 a 149
35 y 36
5. Perímetro y área del
círculo.
Uso de las fórmulas para calcular el perímetro y el área del círculo en la
resolución de problemas.
150 a 153
Resolución de problemas de proporcionalidad múltiple.
154 a 156
AT
32 y 33
M
Bloque 5
31 y 32
IA
Bloque 4
20
N
1. Multiplicación de números
decimales.
ER
Bloque 3
16 y 17
36
6. Problemas de
proporcionalidad múltiple.
8
SACMA1WB_B0.indd 8
30/01/13 10:41
PR
O
M
O
C
IO
N
BLOQUE 1
Eje
Tema
E
Ficha
1
AT
4
Sentido numérico
y pensamiento
algebraico
Problemas
aditivos
• Resolución y planteamiento de problemas que impliquen más
de una operación de suma y resta de fracciones.
Patrones y
ecuaciones
• Construcción de sucesiones de números o de figuras a partir
de una regla dada en lenguaje común.
• Formulación en lenguaje común de expresiones generales que
definen las reglas de sucesiones con progresión aritmética o
geométrica, de números y de figuras.
ER
3
• Representación de números fraccionarios y decimales en la
recta numérica a partir de distintas informaciones, analizando
las convenciones de esta representación.
IA
2
• Explicación del significado de fórmulas geométricas, al
considerar las literales como números generales con los que
es posible operar.
M
5
6
Forma, espacio
y medida
Figuras y cuerpos
8
Proporcionalidad
y funciones
Proporcionalidad
y funciones
9
Nociones de
probabilidad
Nociones de
probabilidad
7
SACMA1WB_B1.indd 9
• Conversión de fracciones decimales y no decimales a su
escritura decimal y viceversa.
L
D
Números y
sistemas de
numeración
Contenido
• Trazo de triángulos y cuadriláteros mediante el uso del juego
de geometría.
• Trazo y análisis de las propiedades de las alturas, medianas,
mediatrices y bisectrices en un triángulo.
• Resolución de problemas de reparto proporcional.
• Identificación y práctica de juegos de azar sencillos y registro
de los resultados.
• Elección de estrategias en función del análisis de resultados
posibles.
25/01/13 20:21
N
En la vida diaria utilizamos números decimales, por ejemplo, las mercancías están dadas en
pesos y centavos, o cuando una medición que no es exacta en números enteros. De igual
manera, ciertas cantidades se expresan en fracciones, como es el caso de algunas medidas
del sistema inglés, por ejemplo, el largo y grueso de clavos y tornillos se expresan en medidas como 3 de pulgada, 1 de pulgada, etcétera. Es importante saber cómo convertir fraccio4
2
nes a su notación decimal y viceversa, ya que así podremos hacer operaciones entre ellas.
IO
sentido numérico y
pensamiento algebraico
Conversión de fracciones a notación
decimal y viceversa
C
Conceptos clave
Las claves del problema
D
E
PR
O
M
O
La madera comercial comúnmente se mide en unidades del sistema inglés: pies, pulgadas y fracciones de pulgada. Supón que un carpintero
necesita cubrir el borde de una tabla de 10 pulgadas de largo × 8 3 de
8
pulgada de ancho con perfil de aluminio para hacer un pequeño pizarrón.
Si el perfil de aluminio tiene una longitud de 56.5 pulgadas, ¿será suficiente para cubrir el borde de la tabla? ¿Le sobrará o le faltará aluminio?,
¿cuánto?
Sí es suficiente la cantidad de perfil de aluminio, porque la tabla tiene
un perímetro de 36.75 pulgadas o 36 3 de pulgadas. Le sobrarán
4
3
19.75 pulgadas o 19 de pulgadas de aluminio.
4
IA
L
1. Selecciona la opción correcta.
a) ¿Qué necesita calcular el carpintero para saber si el aluminio es suficiente
para cubrir el borde de la tabla?
La medida de la diagonal de la tabla.
El área de la tabla.
El área de la tira de aluminio.
El perímetro de la tabla.
ER
manejo
manejo de la información
información
forma, espacio y medida
Desafío matemático
M
AT
b) Las dimensiones de la tabla están dadas en números enteros y fraccionarios, y el largo del aluminio en decimales. ¿Cómo podemos hacer operaciones entre esas cantidades si están expresadas de manera distinta?
Hacemos operaciones con la parte entera del número decimal, el entero y la parte entera del número fraccionario y, por otro lado, sumamos la parte decimal del número decimal con el numerador y el denominador del fraccionario.
Se convierten todas las medidas a números decimales o a fraccionarios.
Hacemos las operaciones con las partes enteras. El resultado será una
buena aproximación.
Convertimos todas las medidas a decímetros.
Una fracción decimal
es aquella en la que el
denominador es un elemento de la sucesión 10,
100, 1 000, 10 000, … .
Ejemplos:
3
7
2
9
,
,
y
10 100 1 000 10 000
Un número decimal es
una expresión que utiliza
punto decimal para separar la parte entera de la
decimal.
Ejemplos:
0.5, 5.67, 0.000 5
Procedimiento
Una forma práctica
de convertir una
fracción decimal
a su notación decimal
es anotar el número que
corresponde al numerador y colocar el punto
decimal de derecha a
izquierda tantas cifras
como ceros tenga el denominador. En caso de
que el número de ceros
del denominador exceda
las cifras del numerador, al número decimal
se le agregan ceros a la
izquierda, tantos como
sea necesario.
Ceros
3
= 0.003 añadidos
1 000
3 ceros
10
SACMA1WB_B1.indd 10
3 cifras
Contenido: Conversión de fracciones decimales y no decimales a su escritura decimal y viceversa.
25/01/13 20:21
3
N
Ahora practica
7
IO
1. Convierte 10 y 100 a notación decimal.
Procedimiento
M
O
5 537
2. Escribe 10 y 100 en notación decimal.
27
O
254
= 25.4 y 5 537 = 55.37
10
100
3
PR
3. Convierte, sin hacer la división, 125 y 4 a notación decimal.
Otra opción es dividir
directamente el numerador entre el denominador.
3
D
2
2
Conceptos clave
IA
L
4. Convierte 3 , 7 y 3 7 a su notación decimal. Si resulta un número
decimal periódico, escríbelo de manera abreviada mediante una línea
horizontal sobre la parte superior del periodo.
ER
3
2
2
= 0.6, 7 = 0.428571 y 3 7 = 3.285714
3
2
Decimal periódico.
Es un número decimal
con un número infinito
de cifras decimales que
se repiten de acuerdo
con determinada secuencia.
M
AT
5. Un recipiente contiene 1.4 L de agua. Si se extraen 5 litros, ¿qué cantidad de líquido contiene ahora el recipiente?
Queda 1 L en el recipiente.
Decimal exacto. Es un
número decimal que
contiene un número
finito de cifras decimales.
manejo
manejo de la información
información
E
27
= 0.216 y 3 = 0.75
125
4
forma, espacio y medida
Las fracciones no
decimales también
pueden representarse
en notación decimal, y
una forma de hacerlo
consiste en convertir la
fracción no decimal a
una decimal equivalente
y después escribir ese
número en notación
decimal.
C
3
= 0.3 y 7 = 0.07
10
100
254
sentido numérico y
pensamiento algebraico
c) Supón que decidiste convertir los números decimales a fracciones para resolver el problema, ¿obtendrías el mismo resultado si hubieras convertido fracciones a decimales?
¿Por qué?
Sí. Porque al hacer las conversiones se obtienen números equivalentes, es decir
tienen el mismo valor.
No. Porque son operaciones diferentes. 7
6. Una escalera de bomberos tiene 10 peldaños separados entre sí por 20 m.
Cada peldaño tiene 0.06 m de grosor. Calcula el largo de la escalera.
El largo de la escalera es de 9.85 m.
(Para obtener este resultado se supuso que la distancia al primer peldaño
7
m
20
0.06 m
7
era de 20 m, y también que esa distancia era la que separaba al último pel-
daño del final de la escalera).
Contenido: Conversión de fracciones decimales y no decimales a su escritura decimal y viceversa.
SACMA1WB_B1.indd 11
11
25/01/13 20:21
sentido numérico y
pensamiento algebraico
7. Fernando hace un recorrido en su motocicleta, cuyo rendimiento es
3
de 23 4 km por litro de gasolina consumido. ¿Cuántos kilómetros puede
recorrer si la capacidad del tanque de la motocicleta es de 15 L , e inicia su trayecto con el tanque lleno? Expresa el resultado con números
decimales.
1
La motocicleta puede recorrer 112.5 km o 112 2 km.
IO
M
O
C
1
kg de diferencia de masa entre Vanessa y Brenda.
2
N
1
8. Brenda tiene una masa de 45.7 kg y la de Vanessa es de 48 5 kg. ¿Cuál
es la diferencia de masa entre ellas?
9. Convierte 0.53, 0.284 y 1.06 a fracciones decimales y, si es posible, a fracciones
comunes.
0.53 = 53 , 0.284 = 284 = 71 y 1.06 = 1 6 = 1 3
1 000
250
100
50
O
100
PR
forma, espacio y medida
Los decimales periódicos se pueden representar mediante una línea
horizontal colocada en la
parte superior del periodo. Ejemplo:
2
= 0.666… = 0.6
3
Hay 2.5 kg o 2
10. Representa 3.687 687…, 3.555… y 0.532 898 9…, con una línea horizontal sobre la
parte superior del periodo.
3.555… = 3.5
0.5328989… = 0.53289
Conceptos clave
D
E
3.687687… = 3.687
3.7 = 3 7
10
y
IA
L
11. Trunca a una cifra decimal 3.687 687… y redondea a centésimos
0.532 898 9. Después convierte las cantidades resultantes a fracciones.
¿Las fracciones obtenidas son equivalentes a los números decimales
periódicos originales? ¿Por qué?
0.53 = 53 . Las fracciones obtenidas no son
ER
manejo
manejo de la información
información
Notación
100
equivalentes a los números periódicos originales porque no se
usaron esos números para crearlas, se emplearon unos números
que se les aproximaban.
AT
M
12. Redondea a cienmilésimos 50.315 548 57 y convierte a fracción el número resultante.
El número 50.31554857 se redondea de la siguiente forma 50.31555
50.31555 = 50 31 555 = 50 6 311
100 000
20 000
13. Encuentra el número que falta en el numerador para que la igualdad
sea correcta.
a) 21 = 4.2
5
12
SACMA1WB_B1.indd 12
b) 18 = 6
3
c) 15 = 3.75
4
d) 10 = 0.1
90
El truncamiento de un
número decimal consiste
en reducir la cantidad de
cifras decimales descartando el resto.
El método común para
el redondeo consiste en
aproximar un número
decimal truncado al valor
más cercano al número
decimal original. Para
ello se siguen dos reglas:
a) Si la cifra decimal
inmediata menor que
la cifra que se quiere
truncar es mayor o
igual que 5, el número
decimal a truncar
se incrementa al
valor inmediatamente
superior.
b) Si la cifra decimal
inmediata menor que
la cifra que se quiere
truncar es menor que
5, el número decimal a
redondear permanece
invariable.
Contenido: Conversión de fracciones decimales y no decimales a su escritura decimal y viceversa.
25/01/13 20:21
14. Encuentra el número que falta en el denominador para que la igualdad sea correcta.
13
5
b) 0.42 =
21
50
c) 0.6 =
3
5
d) 0.54 =
sentido numérico y
pensamiento algebraico
a) 2.6 =
108
200
Regreso al Desafío matemático
IO
N
1. Compara tu solución al Desafío matemático con la de tus compañeros. ¿Todos expresaron los resultados de la misma manera?
Si algunos de tus compañeros expresaron el resultado en notación decimal y otros
como fracción, ¿cómo podrías saber si los resultados son equivalentes? Explícalo.
M
O
decimales y otros están números fraccionarios.
forma, espacio y medida
C
No todos lo resultados se expresaron de la misma manera. Algunos están en números
Para saber si son equivalentes se puede convertir de decimal a fracción o
3
36 4 de pulgadas es lo mismo que
viceversa y comparar los resultados.
O
36.75 pulgadas.
PR
Validación
D
E
manejo
manejo de la información
información
1. En el diagrama siguiente, escribe sobre las líneas las palabras que faltan para completar los enunciados.
3
=
8
8.375
.
Por lo que el perímetro es:
P = 8.375 + 10 + 8.375 + 10 = 30.75
Para sumar
números
representados
por fracciones
y números en
notación decimal
es necesario:
AT
ER
Para resolver
el Desafío
matemático
debemos
obtener el
perímetro del
terreno, éste
se calcula
mediante la
IA
L
En este caso, 8
Convertir las fracciones a
números decimales.
Por lo tanto el sobrante o faltante
es: 17.75 pulgadas
=
3
cuatro lados.
fraccionaria.
M
La suma de los
Convertir los números en
notación decimal a
su representación
1
56
2
En este caso, 56.5 m = .
17
4 pulgadas.
Por lo que el perímetro es:
36 3 .
3
3
4
P=8
+ 10 + 8
+ 10 =
8
Contenido: Conversión de fracciones decimales y no decimales a su escritura decimal y viceversa.
SACMA1WB_B1.indd 13
8
13
25/01/13 20:21
N
La representación de números en una recta numérica es un recurso útil que con frecuencia
se ignora. Leer un termómetro de mercurio, utilizar una taza medidora, entre otras situaciones, son ejemplos en los se requiere una correcta representación de los números en la
recta numérica.
Procedimiento
Para definir la ubicación de los puntos de
una recta numérica hay
que conocer un punto
sobre ella y la unidad de
medida utilizada. Si se
desconoce alguno de
esos dos datos, es posible asignarles un valor,
siempre que se mantengan constantes. Es decir,
después de ubicar un
primer número
sobre una recta numérica no es posible
cambiarlo de lugar, y la
unidad de medida, luego
de definirla, debe ser la
misma para cualquier
punto que se localice en
esa recta.
M
O
C
Daniel participó en una carrera de 15 km. A los diez minutos de empezar
la prueba había recorrido 2 km, después de una hora alcanzó los 11.5 km
y, a una hora y 20 minutos luego de empezar la competencia, le faltaban
0.45 kilómetros para llegar a la meta.
La siguiente recta numérica representa la distancia total de la carrera. Localiza en ella las distancias que se mencionan en el problema.
IO
Desafío matemático
2 km
11.5 km
15 km
PR
0 km
O
14.55 km
Las claves del problema
D
E
a) ¿Cuáles son los números que, de acuerdo con el problema, hay que colocar en la recta?
2 km, 7 km y 15 km 2 km, 11.5 km y 14.55 km
0 km, 10 km y 20 km 2 km, 11.5 km y 20 km
IA
L
b) ¿Por qué es necesario definir una unidad en la recta para ubicar los números que se piden?
No es necesario, siempre es posible ubicar los puntos al tanteo.
Porque es necesario definir una unidad para dividir la recta numérica.
Porque es necesario redondear o truncar las medidas decimales en esa
unidad.
Porque toda la recta representa una unidad.
ER
sentido numérico y
pensamiento algebraico
forma, espacio y medida
manejo
manejo de la información
información
Representación de números fraccionarios
y decimales en la recta numérica
M
AT
c) ¿En cuántas partes se debe dividir la recta para localizar el número que
representa la distancia que Daniel había recorrido a los diez minutos de
iniciar la carrera?
10 partes
2 partes
15 partes
7 partes
d) ¿Entre qué kilómetros se encontraba Daniel después de una hora de
competir?
11 km y 12 km 10 km y 11 km
9 km y 10 km 12 km y 13 km
e) ¿Qué fracción de un kilómetro representa el número decimal 0.5 de la
distancia que Daniel había recorrido en ese tiempo?
1
5 2
1
5
14
SACMA1WB_B1.indd 14
1
1
2
Contenido: Representación de números fraccionarios y decimales en la recta numérica a partir de distintas informaciones, analizando las convenciones de esta representación.
25/01/13 20:21
M
O
forma, espacio y medida
C
IO
N
sentido numérico y
pensamiento algebraico
f) ¿Entre qué kilómetros se encontraba Daniel cuando le faltaban 0.45 km para alcanzar
la meta?
11 km y 12 km
12 km y 13 km
13 km y 14 km
14 km y 15 km
g) ¿Cómo se representa en la recta numérica la distancia a la que se encontraba después
de una hora y 20 minutos?
Se divide la distancia entre el kilómetro 14 y el 15 en 55 partes y se señala la primer
parte.
Se divide la distancia entre el kilómetro 14 y el 15 en 55 partes y se señala la última
parte.
Se divide la distancia entre el kilómetro 14 y el 15 en 10 partes y se señala la quinta
parte.
Se divide la distancia entre el kilómetro 14 y el 15 entre 100 partes y se señala la 55ª
parte.
Ahora practica
A
B
C
D
1
( B) 2 (C) 7 3
3
9
( A) 1 6
D
4
F
( D ) 11
(E ) 4 3
manejo
manejo de la información
información
( F ) 11 E
2
E
0
PR
O
1. En la siguiente recta numérica se ubican los puntos que corresponden a varios números fraccionarios, y cada uno se identifica con una letra. Escribe en los paréntesis
la letra que corresponde a cada número.
6
B
C
D
E
F
G
H
I
ER
A
IA
L
2. La siguiente recta representa una pista de carreras de 100 m, donde hay señales
marcadas con letras. La distancia entre las señales consecutivas es la misma, al igual
que la distancia entre la salida y la primera señal, y la última señal y la línea de meta.
AT
Contesta las preguntas y explica cómo obtuviste la respuesta.
M
a) Cuando un corredor se localiza en la marca C, ¿qué fracción del total de la pista ha
recorrido? ¿A cuántos metros equivale esa distancia?
Ha recorrido 3 de la pista, lo cual equivale a 30 metros.
10
b)Y si un corredor está en la señal G, ¿qué fracción del total de la pista ha recorrido?
¿Cuántos metros le faltan para llegar a la meta?
Ha recorrido 7 de la pista, lo cual equivale a 70 metros.
10
Contenido: Representación de números fraccionarios y decimales en la recta numérica a partir de distintas informaciones, analizando las convenciones de esta representación.
SACMA1WB_B1.indd 15
15
25/01/13 20:21
4
c) Cuando un corredor se localiza a 10 del recorrido, ¿en qué marca se ubica?
7
d) Si a un corredor le faltan por recorrer 10 del total de la pista, ¿en qué marca se encuentra?
En
la C.
Regreso al Desafío matemático
N
sentido numérico y
pensamiento algebraico
En
la D.
IO
1. ¿Qué hiciste para ubicar en la recta numérica las distancias que había recorrido Daniel
durante la carrera? Explícalo.
C
M
O
marca 11 y la del 12. Para encontrar el punto que está a 0.45 de 15 saqué la mitad entre
14 y 15, y dividí entre diez la distancia de 14.5 a 15, la primera línea es 14.55.
O
2. A los 30 minutos de la competencia, Cecilia, otra participante de la carrera, había recorrido 7.125 km, y Daniel se encontraba a 57 km. ¿Quién iba más adelante en la ca8
rrera? Representa las posiciones en la misma recta numérica del Desafío matemático.
Los dos iban a la misma distancia, porque 57 = 7.125.
8
PR
forma, espacio y medida
R. M. Dividí en 15 partes iguales la recta para marcar los 2 km. El 11.5 está a la mitad de la
Validación
E
D
Cuando a Daniel
IA
L
Representar
2 km en la recta
numérica.
ER
manejo
manejo de la información
información
1. Completa los espacios vacíos en el siguiente diagrama.
le faltaban 0.45 km
Para representar la unidad
Como Daniel había
de medida en la recta del
recorrido 2 km le
corresponde el segundo
problema inicial debemos
dividir esa distancia en 15
punto de la recta.
partes. La distancia entre cada
parte representa una unidad
El decimal 0.5 representa
la mitad de un
de medida, es decir, 1 km.
para llegar a la meta
AT
llevaba recorridos
14.55
km.
Entonces, los
números que hay
M
que colocar en la
recta son
2
y
14.55
Representar
11.5 km en la
recta numérica.
entero; por tanto, 11.5
Como 11.5 y 12
es menor que
puntos que en la recta
de una hora de competencia,
11
entre los kilómetros numérica representan
12
Una forma de ubicar
A una hora y 20 minutos
este decimal en la recta
de iniciada la carrera,
numérica es dividir la
100
unidad en Daniel había recorrido 14.55
km. La fracción decimal que
corresponde a 0.55 es
SACMA1WB_B1.indd 16
los kilómetros 11 y 12.
.
.
Representar
14.55 km en la
recta numérica.
16
está exactamente a
la mitad entre los
es mayor que
11.5, Daniel se hallaba, después
y
, 11.5
11
55
100
.
partes y tomar de ella
55
subdivisiones.
Contenido: Representación de números fraccionarios y decimales en la recta numérica a partir de distintas informaciones, analizando las convenciones de esta representación.
25/01/13 20:21
En la vida cotidiana se presentan situaciones en las que es necesario sumar o restar fracciones, y con frecuencia su solución implica realizar más de una operación.
Desafío matemático
Hay varios tipos de fracciones:
• Fracción propia, cuando el numerador es
menor que el denominador; por ejemplo
M
O
Las claves del problema
4
PR
O
1. Selecciona la respuesta correcta de las siguientes preguntas.
a) ¿Cuántos kilogramos utilizó Santiago para la sopa y el plato fuerte?
Expresa el resultado como fracción mixta.
1 3
1 1
1 1
2 1
2
4
4
E
D
4
4
4
IA
4
L
c) ¿Qué operación falta para obtener la cantidad de zanahoria que sobró? Haz la operación.
1
Una resta: 2 1 – 2
Una suma: 2 4 + 2
Una suma: 2 1 – 2 1 8
.
5
• Fracción mixta, cuando
se compone de un número entero y de una
fracción propia; por
ejemplo
3
2
.
5
Cualquier fracción impropia se puede expresar
como fracción mixta, y
cualquier fracción mixta
se puede expresar como
fracción impropia.
Una resta: 2 1 + 2 1
4
4
ER
4
• Fracción impropia,
cuando el numerador
es mayor que el denominador; por ejemplo
4
manejo
manejo de la información
información
b) A partir de la respuesta anterior calcula cuántos kilogramos de zanahoria utilizó en total. Expresa el resultado como fracción mixta.
2 1
2
1 3
23
7
.
8
forma, espacio y medida
C
IO
1
Santiago compró 2 4 kg de zanahorias para preparar la comida. Si para la
sopa utilizó 3 kg, para el plato fuerte también 3 kg y 1 kg para el postre,
4
4
2
¿cuántos kilogramos le quedaron para preparar un jugo?
En total empleo 8 kg, es decir, 2 kg de zanahoria. Por lo tanto, le quedó
4
1
kg de zanahoria para el jugo.
4
.
N
Conceptos clave
sentido numérico y
pensamiento algebraico
Problemas que implican más de una
operación de suma y resta de fracciones
AT
Ahora practica
1
1
3
M
1. Vanessa compró 2 2 kg de manzanas, 1 4 kg de cebollas, 1 4 kg de
mangos, 1 kg de ciruelas, 1 kg de lechuga y 3 1 kg de papas.
2
2
2
a) ¿Cuántos kilogramos de verduras compró en total?
Compró en total 5 1 kilogramos de verduras.
4
b)¿Y cuántos kilogramos de fruta?
Compró 4 3 kilogramos de fruta.
4
Contenido: Resolución y planteamiento de problemas que impliquen más de una operación
de suma y resta de fracciones.
SACMA1WB_B1.indd 17
Procedimiento
Para sumar o restar dos
o más fracciones es
necesario que sus denominadores sean iguales.
Cuando los denominadores son distintos
se pueden convertir a
fracciones equivalentes
con denominadores
iguales.
17
25/01/13 20:21
Cuando se hace una
suma de fracciones
los denominadores
permanecen iguales y se
suman sólo los numeradores. Por ejemplo, es
incorrecto pensar que
2. Durante enero, febrero y marzo los estudiantes de una escuela secundaria recolectaron cartón para reciclar. La tabla muestra los resultados
de la colecta.
A
23 3 kg
B
32 4 kg
Marzo
1
1
es igual a
1+3
4
=
= 1,
2+2
4
1
25 2 kg
4
N
Febrero
IO
Enero
24 3 kg
7
en realidad
3
30 8 kg
31 5 kg
C
Mes.
1
3
4
+
=
= 2.
2
2
2
M
O
Equipo
1
3
+
2
2
a) ¿Cuánto recolectó cada equipo?
El equipo A recolectó 73 7 kg de cartón y el equipo B recolectó 94 29 kg de cartón.
40
O
12
b)¿Cuál fue la diferencia entre la cantidad total recolectada por cada equipo?
PR
La diferencia es de 21 17 kg de cartón.
120
D
E
3. Mariana necesita envolver un regalo, pero sólo dispone de tres tramos de listón que
quiere unir en una sola tira, y con lo que le sobre hacer el moño. Las medidas de los
3
1
listones son 10 8 cm, 10 4 cm y 6 1 cm, y para unirlos necesita pegar 2 1 cm de
2
2
cada extremo del listón que se une con otro.
a) ¿Cuánto suman en total los tres tramos de listón antes de pegarlos?
L
27 1 cm
IA
8
b)¿Cuántos centímetros de listón ocupará Mariana para unirlos?
Ocupará 10 cm.
ER
manejo
manejo de la información
información
Error frecuente
Hay 1 kg de diferencia entre la cantidad de fruta y la de verdura.
2
forma, espacio y medida
sentido numérico y
pensamiento algebraico
c) ¿Cuál es la diferencia entre la cantidad de kilogramos de fruta y la de
kilogramos de verdura?
c) ¿Cuánto mide la tira de los listones después de pegarlos?
AT
La tira mide 17 1 cm porque se usan 10 cm para los tramos.
8
1
M
d)Si para envolver el regalo Mariana necesita 12 2 cm de listón, ¿cuántos centímetros le
quedarán para el moño?
5
Le quedarán 4 8 cm para el moño. (Lo más probable es que necesite otro listón para
el moño.)
3
1
4. Una tabla de 20 4 m de largo se corta de otra de 38 4 m. Si la sierra para cortar
3
1
consume 8 m, ¿cuánto queda de la tabla de 38 4 m después del corte?
Quedaron 17 1 m de la tabla después del corte.
8
18
SACMA1WB_B1.indd 18
Contenido: Resolución y planteamiento de problemas que impliquen más de una operación
de suma y resta de fracciones.
25/01/13 20:21
1
3
3 1 m
1
5. Resuelve la operación 5 2 + 2 5 – 3 4 de dos maneras diferentes y expresa el resultado como fracción mixta. ¿Cuál
procedimiento prefieres? ¿Por qué?
2
sentido numérico y
pensamiento algebraico
2m
2 1 m
El total es 7 7 .
8
6. Los alumnos de un grupo de secundaria quieren construir
porterías de futbol con tubos de plástico. Los diseños que
tienen se presentan a continuación.
a) ¿Cuántos metros de tubo se necesitan para construir cada
diseño?
Para la primera se necesitan 16 3 m de tubo
3
4
2 3 m
IO
4
4
1 3 m
4
M
O
4
forma, espacio y medida
C
y para la segunda, 10 3 m.
N
20
b)¿Cuál es la diferencia en la longitud de tubo utilizado en las
dos porterías?
6m
O
7
8
PR
7. En las siguientes figuras se muestran un cuadrado y un triángulo equilátero con la medida de sus lados.
a) Calcula el perímetro de cada figura.
Perímetro del cuadrado: 2 4 × 4 = 9 3 cm
5
3
× 3 = 4 1 cm
Perímetro del triángulo: 1
4
4
E
manejo
manejo de la información
información
5
D
b)Calcula la diferencia entre ambos perímetros.
9 3 − 4 1 = 5 7 cm
20
1 3 cm
4
L
4
5
IA
5
2 4 cm
ER
8. Una empresa exporta sus productos a varios países. La siguiente tabla muestra las
fracciones del total de las ventas a cada país en los años indicados.
País
AT
Año
Fracciones de ventas totales
Bolivia
Argentina
Colombia
Perú
Venezuela
1
20
1
5
1
4
1
6
1
3
2011
1
10
2
15
1
4
1
6
7
20
M
2010
a) ¿Cuál fue la diferencia en las ventas entre Venezuela y Perú en 2011?
La diferencia es de 11 .
60
b)¿Qué fracción del total de las ventas suman las exportaciones realizadas en 2010 a
Colombia, Argentina y Bolivia?
El total de ventas fue de 1 .
2
Contenido: Resolución y planteamiento de problemas que impliquen más de una operación
de suma y resta de fracciones.
SACMA1WB_B1.indd 19
19
25/01/13 20:21
c) ¿Cuál fue en 2010 la fracción de diferencia entre las ventas a Colombia y Argentina
comparadas con las ventas a Bolivia y Perú?
La diferencia entre las ventas de estos países fue de 7 .
sentido numérico y
pensamiento algebraico
30
d)¿Cuál fue en 2011 la diferencia entre las exportaciones a Colombia y Perú, comparadas
con las que se realizaron a Venezuela y Bolivia?
La diferencia entre las exportaciones de esos países fue de 1 .
IO
1
C
M
O
Se emplearon 52 7 cm para hacer el moño.
O
8
Regreso al Desafío matemático
IA
L
D
E
Explica cómo resolviste el Desafío matemático del inicio. Con base en lo que repasaste en
esta ficha, ¿consideras que tu respuesta es correcta? Corrígela si es necesario.
1. ¿Con los kilogramos de zanahoria que le sobraron a Santiago es suficiente para hacer
otra sopa igual a la primera? ¿Por qué?
No, porque le faltan 2 kg de zanahoria para los 3 kg que empleó
4
4
para la sopa. Sólo le queda 1 kg.
4
ER
manejo
manejo de la información
información
1
9. A una caja de regalo de dimensiones 10 8 cm × 10 4 cm × 6 2 cm se ata una
cinta como muestra la figura. Si la cinta que se empleó medía 80 cm, ¿cuánta
cinta se utilizó para el moño?
PR
forma, espacio y medida
3
N
30
Validación
M
AT
1. Escribe sobre las líneas las palabras que faltan para completar los enunciados del
diagrama. Después verifica con tus respuestas si tu respuesta inicial al Desafío matemático es correcta.
Para resolver el Desafío
Después, para conocer el total
matemático primero debemos
de kilogramos de zanahoria que
saber cuántos kilogramos de
necesitó Santiago para la comida,
zanahorias necesitó Santiago
hay que sumar el resultado anterior
para la sopa y el plato fuerte, lo
3
cual se obtiene al sumar 4 kg
1
3
1
y 4 kg, que es igual a 2 kg.
y la cantidad que usó para el postre,
20
SACMA1WB_B1.indd 20
es decir:
1
1
2
Finalmente, hay que restar
1
kg + 2
kg = 2
kg.
la cantidad de kilogramos
de zanahoria que tenía al
principio y la que usó para
toda la comida:
1
2
4 ­­– 2 kg =
1
4
kg.
Contenido: Resolución y planteamiento de problemas que impliquen más de una operación
de suma y resta de fracciones.
25/01/13 20:21
Sucesiones de números y de figuras
Desafío matemático
PR
O
Para hacer la figura que sigue se necesita agregar un cuadrado
AT
D
ER
IA
L
1. Selecciona la respuesta correcta de las siguientes preguntas.
a) ¿Cuántos cuadrados se agregan para pasar de una figura a la siguiente y cómo se acomodan?
Se agregan seis cuadrados: dos en cada extremo de la figura original.
Se agregan cuatro cuadrados: uno en cada extremo superior de la
figura y dos en la parte inferior de la columna.
Se agregan tres cuadrados: uno en cada extremo de la figura original.
Se agregan tres cuadrados: uno en el cruce de las tiras de cuadrados
y dos más en los extremos superiores.
M
b) ¿El tipo de progresión de la sucesión de figuras es aritmética o geométrica? Justifica tu respuesta.
Es de progresión aritmética porque la diferencia entre el número de
cuadros de una figura y su sucesora es un número constante.
Es de progresión aritmética porque el cociente entre el número de
cuadrados de una figura y su antecesora es un número constante.
Es de progresión geométrica porque el cociente entre el número de
cuadrados de una figura y su antecesora es un número constante.
Es de progresión geométrica porque la diferencia entre el número de
cuadrados de una figura y su antecesora es un número constante.
La progresión de una
sucesión es la manera
en la que se obtiene un
elemento a partir del
anterior:
• La progresión de las
sucesiones en las que
la diferencia entre un
término y su antecesor
(el término anterior a él)
es un número constante se llama progresión
aritmética. Por ejemplo,
la sucesión 2, 4, 6, … tiene progresión aritmética, ya que la diferencia
entre un término y su
antecesor es siempre 2.
• La progresión de las
sucesiones en las que
el cociente entre un
término y su antecesor
es un número constante se llama progresión geométrica. Por
ejemplo, la sucesión 2,
4, 8, 16, … tiene progresión geométrica ya que
el cociente entre un
término y su antecesor
siempre es 2.
Contenido: Construcción de sucesiones de números o de figuras a partir de una regla dada en lenguaje común. Formulación en lenguaje común de expresiones generales que definen las reglas de sucesiones con progresión aritmética o
geométrica, de números y de figuras.
SACMA1WB_B1.indd 21
manejo
manejo de la información
información
E
a cada extremo de la figura anterior.
Las claves del problema
IO
M
O
Figura 3
forma, espacio y medida
Figura 2
Cada elemento de una
sucesión numérica se
denomina término y
cuando se habla de primero, segundo, etcétera,
se indica la posición que
ocupa en la sucesión; por
ejemplo, en la sucesión
numérica 8, 10, 12, …
el primer término es el
número 8; el segundo, el
10, y el tercero, el 12.
C
Figura 4
N
Conceptos clave
Describe con tus propias palabras la regla que define la siguiente sucesión de figuras y dibuja la cuarta.
Figura 1
sentido numérico y
pensamiento algebraico
Las sucesiones son conjuntos infinitos de números o de figuras que cumplen dos condiciones: tienen un primer elemento y todos los siguientes se obtienen a partir del anterior mediante una regla. Algunas sucesiones numéricas que conoces son, por ejemplo, los números
naturales (1, 2, 3, 4, 5,…), los números pares (2, 4, 6, 8,…) y los números impares (1, 3, 5, 7,…).
21
25/01/13 20:21
1. Obtén los primeros cinco términos de cada sucesión a partir del primer término
aplicando la regla que se indica. Señala también de qué tipo de progresión se trata.
a) El primer término es 2 y el siguiente se obtiene sumando tres al anterior.
Progresión aritmética: 2, 5, 8, 11, 14…
b)Para pasar de un término a otro, el antecesor se multiplica por cuatro, y
la sucesión empieza en 4.
2
Los términos de una
sucesión numérica se
escriben separados por
comas, y después de
escribir algunos, ya que
no es posible escribirlos
todos, se agregan tres
puntos suspensivos, lo
que indica que la sucesión no termina; por
ejemplo: 5, 10, 15, 20,… o
12, 24, 48, 96,…
C
2
2
M
O
forma, espacio y medida
1
c) Cada término se obtiene al sumar 2 al anterior; el primer término es 1 .
2
1
3
5
Progresión
aritmética:
,
1,
,
2,
…
N
Progresión geométrica: 4, 16, 64, 256, 1024…
Notación
IO
sentido numérico y
pensamiento algebraico
Ahora practica
PR
Progresión geométrica: 5, 10, 20, 40, 80…
O
d)La sucesión comienza en 5 y cada término se obtiene al multiplicar por
dos al anterior.
D
E
Progresión geométrica: 40, 20, 10, 5, 2.5…
L
f) La sucesión inicia en 100 y para obtener el siguiente elemento al anterior se le suma
veinticinco.
IA
Progresión aritmética: 100, 125, 150, 175, 200…
ER
2. Relaciona ambas columnas. Escribe en el paréntesis la letra que corresponde a la
regla que describe la sucesión. Indica en cada caso si se trata de una progresión
aritmética, geométrica o ninguna de las dos.
AT
manejo
manejo de la información
información
e) El primer elemento de la sucesión es el 40 y el siguiente se obtiene dividiendo entre
dos al anterior.
Regla
A. Se suma 1 para obtener cada término.
Progresión
Tipo de progresión
Aritmética
B. Para pasar al siguiente término se multiplica al
anterior por dos y se resta uno.
( E ) 16, 8, 4, 2, 1, 0.5,…
Geométrica
C. Se multiplica por 3 para obtener cada uno de
los siguientes términos.
( C ) 4, 12, 36, 108, 324,…
Geométrica
D. Se suma 0.5 para obtener el siguiente término.
( A ) 1, 1 1 , 1 2 , 2, 2 1 ,…
Aritmética
E. Cada término se genera al dividir entre dos el
anterior.
( B ) 2, 3, 5, 9, 17,…
M
( D ) 1.5, 2, 2.5, 3, 3.5,…
22
SACMA1WB_B1.indd 22
3
3
3
3
Ninguna de las dos
Contenido: Construcción de sucesiones de números o de figuras a partir de una regla dada en lenguaje común. Formulación en lenguaje común de expresiones generales que definen las reglas de sucesiones con progresión aritmética o
geométrica, de números y de figuras.
25/01/13 20:21
N
sentido numérico y
pensamiento algebraico
3. Dibuja los siguientes dos elementos de la sucesión formada a partir
de una letra F hecha de cuadrados, en la que de una figura a la siguiente se agrega un cuadrado a cada extremo.
Una sucesión de figuras
es un conjunto de figuras
generadas a partir de un
patrón definido.
(
Sucesión numérica
)
A. 1, 4, 9, 16,…
M
O
Sucesión de figuras
forma, espacio y medida
C
4. Escribe la regla que define cada una de las siguientes sucesiones de
figuras y relaciónala con la sucesión numérica correspondiente. Indica
si el tipo de progresión es aritmética, geométrica o ninguna de las dos.
IO
Conceptos clave
Regla. Tipo de sucesión
O
A cada lado del cuadrado se agrega un punto,
se distribuyen los puntos de manera equitativa
(
PR
sobre cada lado. Progresión aritmética.
)
B. 1, 2, 3, 4,…
A cada extremo se le agrega un cuadrado
)
D
(
C. 1, 3, 5, 7,…
ER
)
Del lado izquierdo se le agrega el número de
triángulos que corresponde a la sucesión
de impares, es decir, al segundo término se le
agregan 3, después 5, luego 7, y así sucesivamente. Ninguna de las dos.
D. 5, 9, 13, 21,…
Se agregan dos triángulos del lado izquierdo.
Progresión aritmética.
E. 4, 8, 12, 16,…
Se agrega una línea al lado izquierdo, en el
sentido de las manecillas del reloj. Progresión
aritmética.
M
AT
(
IA
L
)
aritmética.
manejo
manejo de la información
información
(
E
con respecto a la figura anterior. Progresión
5. Escribe con tus propias palabras la regla que define cada sucesión. No olvides indicar cuál es su primer término, así como de qué tipo de progresión se trata (aritmética, geométrica o ninguna de las dos).
El primer término es 5 y se suma 3 al término anterior para obtener
el siguiente. Progresión aritmética.
b)9, 9.1, 9.2, 9.3, 9.4,… El primer término es 9 y se suma 0.1 al término anterior para
obtener el siguiente. Progresión aritmética.
c) 30, 15, 7.5, 3.75, 1.875,… El primer término es 30 y se divide entre 2 al término anterior para obtener el siguiente. Progresión geométrica.
a) 5, 8, 11, 14, 17,… Contenido: Construcción de sucesiones de números o de figuras a partir de una regla dada en lenguaje común. Formulación en lenguaje común de expresiones generales que definen las reglas de sucesiones con progresión aritmética o
geométrica, de números y de figuras.
SACMA1WB_B1.indd 23
23
25/01/13 20:21
sentido numérico y
pensamiento algebraico
6. Escribe los siguientes tres términos de cada sucesión e indica si se trata de
una progresión aritmética o geométrica.
a) 2, 13, 24, 35, 46, 57, 68
,
79
,
90
,…
220
,
240
,
260
,…
,
1
4
,
1
16
Progresión aritmética
b)140, 160, 180, 200, Progresión aritmética
2
1
2
,
4
1 041 2
3
,
5 208 1
3
,…
M
O
Figura 3
7. Describe con tus propias palabras la regla que define la siguiente sucesión de
figuras.
O
Se agrega una fila al final de la escalera con un cuadrado más que la anterior última fila y se quitan todos los cuadrados que no estén en el contorno de la figura.
Figura 4
E
Regreso al Desafío matemático
PR
forma, espacio y medida
208 1
C
1
d) 3 , 1 3 , 8 3 , 41 3 , Progresión geométrica
N
,…
IO
1
c) 256, 64, 16, 4, Figura 2
Progresión geométrica
ER
Respuesta libre.
IA
L
D
1. Compara tu respuesta al Desafío matemático con la de tus compañeros y verifica si
es correcta.
a) Analiza el número de cuadritos de cada figura y contesta si la sucesión numérica que
Es una progresión aritmética.
se forma es geométrica o aritmética. 2. Inventa una sucesión de figuras, escribe la regla que la defina y dibuja los primeros
cinco elementos que la integran.
AT
manejo
manejo de la información
información
Figura 1
Validación
M
1. En el diagrama siguiente, escribe sobre las líneas las palabras que faltan para completar los enunciados.
La primera figura
representa la letra
T
que está compuesta
5
por
cuadrados.
24
SACMA1WB_B1.indd 24
,
Para pasar a la siguiente figura
se agregan 3
cuadrados
a la anterior: en cada uno de
los extremos de la figura inicial
se agrega(n) 1
cuadrado.
Es una sucesión con
progresión aritmética ,
ya que la diferencia entre
términos consecutivos es
constante.
Contenido: Construcción de sucesiones de números o de figuras a partir de una regla dada en lenguaje común. Formulación en lenguaje común de expresiones generales que definen las reglas de sucesiones con progresión aritmética o
geométrica, de números y de figuras.
25/01/13 20:21
Significado de fórmulas geométricas
Desafío matemático
sentido numérico y
pensamiento algebraico
En diversas áreas del conocimiento se emplean fórmulas para simplificar la obtención de resultados y estudiar los fenómenos propios de cada disciplina. Una fórmula es una igualdad
que establece relaciones entre variables (literales) y números (constantes) mediante operaciones aritméticas básicas (suma, resta, multiplicación, división, potencia, raíz, etcétera).
N
Conceptos clave
Las literales de una
fórmula representan números variables, es decir,
cantidades que pueden
cambiarse. Es una manera de expresar de manera general diferentes
tipos de magnitudes.
M
O
Las claves del problema
forma, espacio y medida
C
IO
Angélica compró tres vitrales cuadrados del mismo tamaño y quiere colocar cinta protectora en el borde de cada uno. Si cada lado de los vitrales
mide 80 cm, ¿cómo puede determinar cuánta cinta necesita en total, sin
calcular la cantidad necesaria que requiere cada vitral? Escribe una fórmula para calcularla y otra más general que permita obtener la cantidad
de cinta necesaria para cualquier número de vitrales de cualquier tamaño.
(3 × 4 × 80) cm; Número de vitrales × (4 × lado)
Ejemplo: para calcular
el área de un rectángulo, se tiene la fórmula
Á = b × h, donde Á es la
variable que representa
el área y b y h son las variables que representan
la longitud de los lados
y que pueden cambiar,
para distintos rectángulos.
PR
O
a) ¿Cuál es la fórmula para calcular el perímetro de un cuadrado cuyo lado
mide z unidades?
z × z
4z
z × z × z × z
z2
L
IA
Ahora practica
D
E
manejo
manejo de la información
información
b) A partir de la respuesta anterior, ¿con qué fórmula puedes calcular el perímetro de los tres vitrales?
z × z × 3
12z
4z + 3
3 + z2
ER
1. Calcula el perímetro de los siguientes triángulos equiláteros.
a) ¿Cómo determinaste el perímetro en cada caso?
Se multiplica por 3 la medida de un lado.
b)¿Cuál es el perímetro de un triángulo equilátero de 8.2 cm?
AT
24.6 cm
4 cm
P = 12
M
c) ¿Con qué fórmula puedes obtener el perímetro de cualquier
triángulo equilátero?
P = 3l
2. Calcula el perímetro de estos cuadrados.
a) ¿Con qué fórmula puedes obtener el perímetro de cualquier
cuadrado?
P = 4l
b)Utiliza la fórmula anterior para calcular el perímetro de tres
cuadrados, cuyos lados miden 9 km, 11.5 m y 4.2 cm, respec
El perímetro del primero es de 36 km; el del setivamente.
gundo de 46 m, y el del tercero de 16.8 cm.
3 cm
P = 48
cm
P = 9
cm
P =40
12 cm
Contenido: Explicación del significado de fórmulas geométricas, al considerar las literales como números generales
con los que es posible operar.
SACMA1WB_B1.indd 25
cm
cm
10 cm
25
25/01/13 20:21
3.5 cm
Nombre: Rombo
4l
Fórmula: 14 m
P=
N
Nombre: Rectángulo
Fórmula: 2b + 2h
14 cm
P=
2 cm
5 cm
6 mm
C
2m
Trapecio
Nombre: escaleno
Fórmula: a + b + c + d
15 m
P=
M
O
3m
Nombre: Romboide
Fórmula: 2b + 2c
20 mm
P=
4 mm
O
6m
PR
d)Explica por qué con las fórmulas anteriores se puede calcular el perímetro de cualquier
otro polígono con el mismo nombre.
Porque las literales pueden tomar cualquier valor que les asignes.
D
E
4. ¿Cuál es la fórmula que permite conocer el perímetro de cada uno de los siguientes
polígonos regulares? Utiliza la literal que se indica.
k
t
IA
L
z
Fórmula: 5z
ER
manejo
manejo de la información
información
forma, espacio y medida
4m
IO
sentido numérico y
pensamiento algebraico
3. Realiza lo que se pide para cada una de las siguientes figuras.
a) Indica su nombre.
b)E scribe la fórmula general para calcular su perímetro (utiliza las literales que prefieras).
c) Calcula su perímetro empleando la fórmula.
Fórmula: 6k
Fórmula: 7t
AT
4 cm
a) ¿Las fórmulas que anotaste sirven para calcular el perímetro de cualquier otro
polígono regular con el mismo número de lados? Justifica tu respuesta.
M
Sí, porque las literales pueden tomar cualquier valor.
5. Calcula el área de los siguientes triángulos.
a) Explica el procedimiento que seguiste para obtener las áreas. 3 cm
A=6
cm
2
4.5 cm
Se multiplica la base por la altura y se divide entre dos.
b)¿Cuál es la fórmula general con la que se obtiene el área de cualquier triángulo? Utiliza la literal b para indicar la medida de la base y la a para la altura.
bh
A = 2
26
SACMA1WB_B1.indd 26
6 cm
cm2
A = 13.5
Contenido: Explicación del significado de fórmulas geométricas, al considerar las literales como números generales
con los que es posible operar.
25/01/13 20:21
c) ¿Cuál es el área de un triángulo cuya base mide 250 cm y su altura 400 cm? sentido numérico y
pensamiento algebraico
100 000 cm2
d)Compara la fórmula para obtener el área de un triángulo con la de un rectángulo. ¿Qué
semejanzas y diferencias observas?
El área de un tríángulo es la mitad que la de un rectángulo con las mismas medidas.
N
e) ¿Podrías obtener el área de un triángulo a partir de un rectángulo, como modelo, con
la misma base y altura? Justifica tu respuesta.
M
O
forma, espacio y medida
6. Calcula el área de los cuadrados.
a) Explica el procedimiento que seguiste para obtener las áreas.
C
dividir el área del rectángulo entre dos.
IO
Sí, puesto que los valores de los lados son los mismos. Sólo sería necesario
7 cm
Se multiplica un lado por sí mismo (se eleva al cuadrado).
Área =49
cm2
O
b)Escribe la fórmula general para calcular el área de un cuadrado.
PR
A = l × l
4.5 cm
Área =20.25
cm2
manejo
manejo de la información
información
E
D
Regreso al Desafío matemático
IA
L
Regresa al problema del Desafío matemático y, con base en lo que practicaste, revisa si
tu respuesta es correcta. Corrígela en caso necesario. En la fórmula que propusiste, ¿qué
literales y constantes empleaste?
ER
La única constante es 4, el número de lados del vitral. Las literales son el número de vitrales
y la medida del lado. (El educando es libre de asignar las literales que deseé a estas variables.)
M
AT
Angélica compró cuatro vitrales más, todos del mismo tamaño y con forma de hexágonos regulares, que también protegerá con cinta. ¿Con qué fórmula puede saber
cuánta cinta necesitará para los cuatro vitrales? 4 × 6 × l
Validación
1. Completa los espacios vacíos en el diagrama siguiente.
Para calcular cuánta cinta
se requiere en un vitral es
necesario calcular el perímetro
del vitral.
Para calcular el perímetro de
Para calcular cuánta cinta se
un vitral hay que sumar m
4
veces.
necesita para los tres vitrales hay
que sumar m 12 veces.
Contenido: Explicación del significado de fórmulas geométricas, al considerar las literales como números generales
con los que es posible operar.
SACMA1WB_B1.indd 27
27
25/01/13 20:21
N
Los triángulos y cuadriláteros son dos de las formas más simples que se pueden trazar si se
tiene, un juego de geometría. A su vez, algunas formas más complejas se pueden formar
mediante la combinación de triángulos y cuadriláteros, por eso es importante manejar las
técnicas de sus trazos.
Procedimiento
Desafío matemático
IO
M
O
C
Alberto necesita recortar cinco piezas triangulares de madera para el
acabado de un mueble. Los lados de los triángulos deben medir 3, 4 y 5
centímetros. Usa regla y compás para trazar un triángulo como los que
necesita Alberto.
Para construir un triángulo dados tres de sus
lados a, b y c, se realizan
los pasos siguientes.
Las claves del problema
O
a) ¿Qué dificultad hay para trazar el triángulo sólo con escuadra y regla?
La dificultad de realizar medidas exactas.
Hacer coincidir los lados del triángulo.
No hay dificultad, es fácil trazarlo con esas herramientas.
Tener sólo una escuadra en forma de triángulo isósceles.
1. Con la regla se traza
una línea (a la que
llamamos b) cuyos
extremos constituirán
los vértices A y C del
triangulo; de tal forma
que AC = b.
PR
2. Con el compás se
traza un arco con
centro en A y radio
con longitud igual al
lado c.
b) ¿Cuál es el primer paso para trazar el triángulo con compás y regla?
Trazar una circunferencia con el diámetro igual a uno de los lados.
Trazar el ángulo que forman dos lados del triángulo.
Trazar un lado del triángulo.
Trazar dos lados del triángulo.
D
E
3. Se traza un arco con
centro en C y radio a
y se llama B al punto
donde se intersecan
ambos arcos.
IA
L
4. Para finalizar se trazan
los segmentos BC y
AB. El △ ABC es el
triángulo formado.
c) ¿Por qué es útil el compás para trazar el triángulo?
Porque mantiene una medida constante entre el centro y cualquier
punto de la circunferencia.
Porque su punta tiene un lápiz para trazar.
Porque se pueden trazar círculos concéntricos de diferentes diámetros.
Porque el área de un círculo depende de la medida de su radio.
a
ER
sentidonumérico
numéricoyy
sentido
pensamientoalgebraico
algebraico
pensamiento
forma, espacio y medida
b
c
B
AT
manejo
manejo de la información
información
Trazo de triángulos y cuadriláteros
mediante el uso del juego de geometría
M
c
w
Ahora practica
b
C
cm
4.5 cm
1. Elige los instrumentos adecuados de tu juego de geometría y reproduce en tu cuaderno, con las medidas indicadas, el siguiente triángulo.
7.5
A
a
6 cm
28
SACMA1WB_B1.indd 28
Contenido: Trazo de triángulos y cuadriláteros mediante el uso del juego de geometría.
25/01/13 20:21
2. Traza en tu cuaderno un triángulo isósceles cuyos sus lados iguales midan 8 cm y el
lado diferente, 4 cm. ¿Qué instrumentos utilizarás?
sentido numérico y
pensamiento algebraico
Necesitaré regla graduada y compás.
3. Construye un triángulo con las medidas de la siguiente figura.
Notación
4.83 cm
En un cuadrilátero se llaman lados opuestos los
que no comparten algún
vértice, y lados consecutivos aquellos que
comparten un vértice.
N
2.79 cm
IO
53 o
27 o
6 cm
PR
O
M
O
forma, espacio y medida
C
4. Reproduce con escuadra y compás la siguiente figura.
E
manejo
manejo de la información
información
D
5. Traza con compás, regla y transportador un triángulo. Uno de sus lados debe medir
3 cm, otro 5 cm y el ángulo entre esos lados será de 30°. ¿Qué medida tiene el tercer lado?
ER
IA
L
2.83 cm
AT
6. Construye un romboide con un lado de 3 cm, cualquier lado consecutivo de 5 cm y
el ángulo entre ellos de 38°. ¿Qué medida tienen los otros tres ángulos?
M
38° , 142° y 142°
7. Selecciona la proposición verdadera y traza en tu cuaderno un cuadrilátero que
ejemplifique tu respuesta.
a) Un cuadrilátero puede tener cuatro ángulos agudos.
b)Un cuadrilátero puede tener dos ángulos agudos y dos obtusos.
c) Un cuadrilátero puede tener dos ángulos rectos y dos agudos.
Contenido: Trazo de triángulos y cuadriláteros mediante el uso del juego de geometría.
SACMA1WB_B1.indd 29
29
25/01/13 20:21
Procedimiento
N
9. Traza en tu cuaderno un trapecio que tenga los mismos ángulos del
trapecio anterior y sus los lados del doble del tamaño.
M
O
3 cm
O
3 cm
6 cm
4. Se construye el ∠ A
con AC como uno de
sus lados y con vértice
en A.
5. La intersección de los
lados de los ángulos
∠ A y ∠ C distintos de
b es B.
E
L
D
2.5 cm
2 cm
IA
ER
4.5 cm
A
b
B
1.5 cm
9 cm
w
M
AT
manejo
manejo de la información
información
2 cm
4.5 cm
1.5 cm
2. En el punto C se traza
un ángulo de medida
igual a ∡ A + ∡ B de tal
modo que la prolongación de AC sea uno
de sus lados.
3. El complemento de la
suma de los ángulos
∠ A y ∠ B será ∠ C.
PR
1.5 cm
3 cm
1. Se traza una línea
de longitud b, cuyos
extremos nombraremos A y C y que serán
vértices del triángulo,
de modo que AC = b.
C
10. Reproduce en tu cuaderno, con tu juego de geometría, los siguientes
cuadriláteros.
forma, espacio y medida
Para construir un
triángulo dados dos de
sus ángulos ∠ A y ∠ B y
un lado b que no forme
parte del ángulo B.
IO
sentidonumérico
numéricoyy
sentido
pensamientoalgebraico
algebraico
pensamiento
8. Mide con trasportador y regla los ángulos y lados del siguiente trapecio
y reprodúcelo en tu cuaderno.
1.5 cm
4.5 cm
A
b
c
1.5 cm
4.5 cm
6 cm
30
SACMA1WB_B1.indd 30
Contenido: Trazo de triángulos y cuadriláteros mediante el uso del juego de geometría.
25/01/13 20:21
11. Construye un rombo cuyos lados midan 3.8 cm y dos de sus ángulos sean de 60°.
60°
3 cm
12. Dibuja un romboide y un
trapezoide con dos lados de 3 cm y dos lados
de 5 cm cada figura.
IO
N
5 cm
5 cm
forma, espacio y medida
M
O
3 cm
C
5 cm
5 cm
3 cm
PR
Regreso al Desafío matemático
O
3 cm
sentido numérico y
pensamiento algebraico
60°
1. Describe el procedimiento que seguiste para trazar un triángulo como el que Alberto
necesitaba para hacer su mueble. ¿Cómo puedes saber si el procedimiento es correcto?
manejo
manejo de la información
información
E
Trazar
una recta de 5 cm. En una punta hacer un círculo de 3 cm y en la otra uno de
D
4
cm. Unir las puntas con el punto de intersección.
ER
IA
L
2. Para terminar su mueble Alberto también necesita tres piezas de madera en forma de
triángulo isósceles, cuyo lado desigual sea de 4 cm y sus lados iguales de 6 cm cada
uno. Traza en tu cuaderno con regla y compás un triángulo como el que necesita
Alberto.
Validación
AT
1. Llena los espacios vacíos en el diagrama siguiente para completar los enunciados.
M
Una manera de
Después, con ayuda del
compás se trazan dos
circunferencias
:
resolver el Desafío
matemático
una en un extremo
consiste en trazar
del lado trazado del
primero con la
triángulo cuyo radio
regla uno de los
lados
sea igual a otro lado del
del triángulo.
otro extremo y con un
triángulo, y otra en el
radio igual al tercer lado.
Dos vértices del
triángulo son
Para finalizar se
los extremos del
trazan con la regla
primer segmento
dos líneas rectas:
trazado y el tercero
una desde cada
extremo
es el punto de
intersección
de las circunfe-
al tercer vértice.
rencias.
Contenido: Trazo de triángulos y cuadriláteros mediante el uso del juego de geometría.
SACMA1WB_B1.indd 31
del lado ya trazado
31
25/01/13 20:21
Una de las características interesantes que cumplen todos los triángulos son las llamadas
rectas notables: la altura, la mediana, las mediatriz y la bisectriz.
Desafío matemático
Conceptos clave
N
A
Traza una circunferencia que pase
por los tres vértices de este triángulo.
C
M
O
C
PR
O
B
L
D
E
b) Para trazar una circunferencia que pase por los puntos A, B, y C del triángulo es necesario que:
El centro de la circunferencia coincida con uno de los vértices del
triángulo.
El perímetro de la circunferencia sea igual al perímetro del triángulo.
La distancia del centro de la circunferencia a cada vértice sea la misma.
La circunferencia sea tangente a los lados del triángulo.
ER
IA
c) Para cumplir la condición del reactivo anterior es necesario:
Trazar una circunferencia cuyo centro coincida con uno de los vértices
del triángulo y su radio sea igual a la longitud de uno de sus lados.
Medir el perímetro del triángulo y determinar el radio de la circunferenC
cia con la fórmula = .
2π
Localizar el circuncentro del triángulo.
Localizar el incentro del triángulo.
AT
manejo
manejo de la información
información
forma, espacio y medida
Las claves del problema
a) ¿Qué nombre recibe la circunferencia que pasa por los vértices de una figura geométrica?
Inscrita
Circunscrita
Exterior
Circundante
La altura de un triángulo es el segmento de
recta perpendicular a
un lado del triángulo (o
su prolongación) que va
al vértice opuesto a ese
lado.
La mediana de un triángulo es el segmento que
une el punto medio de
un lado del triángulo y
el vértice opuesto a ese
lado.
La mediatriz en un
triángulo es la recta que
pasa perpendicularmente por el punto medio
de uno de los lados del
triángulo.
La bisectriz en un
triángulo es la recta
que divide en dos partes
iguales un ángulo del
triángulo.
IO
sentidonumérico
numéricoyy
sentido
pensamientoalgebraico
algebraico
pensamiento
Propiedades de las rectas notables
del triángulo
M
d) El paso anterior se obtiene si:
Primero se trazan las alturas del triángulo.
Primero se trazan las medianas del triángulo.
Se trazan las mediatrices del triángulo.
Se trazan las bisectrices del triángulo.
32
SACMA1WB_B1.indd 32
Contenido: Trazo y análisis de las propiedades de las alturas, medianas, mediatrices y bisectrices en un triángulo.
25/01/13 20:21
Ahora practica
C
sentido numérico y
pensamiento algebraico
1. Relaciona las rectas notables del siguiente triángulo con su respectivo
nombre.
D
Conceptos clave
Las alturas de un triángulo se intersecan en
un solo punto llamado
ortocentro.
Las medianas de un
triángulo coinciden en
un punto llamado baricentro.
Las mediatrices de los
lados de un triángulo
coinciden en un solo
punto llamado circuncentro, que es el centro
de la circunferencia
circunscrita, que pasa
por los tres vértices del
triángulo.
Incentro es el punto
en el que se intersecan
las bisectrices de un
triángulo. El incentro es
el centro de la circunferencia que toca cada
lado del triángulo en un
solo punto, y se llama
circunferencia inscrita.
N
B
A
PR
O
M
O
forma, espacio y medida
C
2. Traza en cada triángulo las rectas notables necesarias para determinar
dónde se localiza el punto indicado; también traza la circunferencia
circunscrita e inscrita en los casos correspondientes.
IO
( D ) Mediatriz
( B ) Bisectriz
( C ) Altura
( A ) Mediana
manejo
manejo de la información
información
D
E
Baricentro
Circuncentro
M
AT
ER
IA
L
Ortocentro
Incentro
Contenido: Trazo y análisis de las propiedades de las alturas, medianas, mediatrices y bisectrices en un triángulo.
SACMA1WB_B1.indd 33
33
25/01/13 20:21
Incentro
Ortocentro
Baricentro
Acutángulo
Dentro del
tríangulo
Dentro
del triángulo
Dentro del
tríangulo
Dentro del
tríangulo
En el punto
medio de la
hipotenusa
Fuera del
tríangulo
Dentro del
tríangulo
En un vértice
del triángulo
Dentro del
tríangulo
Dentro del
tríangulo
Fuera del
tríangulo
Dentro del
tríangulo
Rectángulo
O
1. Describe tu procedimiento para resolver el Desafío matemático y resuelve el siguiente problema.
Hay
que obtener las mediatrices del triángulo y después trazar una cir
cunferencia
con centro en el circuncentro y radio en cualquier vértice.
D
E
a) Una empresa de telecomunicaciones debe construir una torre con antenas entre tres ciudades. En la siguiente figura se representan con las
letras A, B y C. ¿Dónde se debe construir la antena para que se ubique a
la misma distancia de las tres ciudades?
IA
L
B
ER
manejo
manejo de la información
información
Conceptos clave
C
Regreso al Desafío matemático
PR
forma, espacio y medida
Obtusángulo
N
Circuncentro
El triángulo acutángulo
es el que tiene todos su
ángulos internos agudos
o menores que 90o.
Los triángulos rectángulos tienen un ángulo
recto, es decir, de 90o.
Un triángulo obtusángulo tiene un ángulo
obtuso, es decir, mayor
de 90o.
IO
Punto
notable
Tipo de
triángulo
Conceptos clave
M
O
sentidonumérico
numéricoyy
sentido
pensamientoalgebraico
algebraico
pensamiento
3. Traza en tu cuaderno los siguientes triángulos para completar la tabla.
Indica la ubicación de los puntos notables según el triángulo de que se
trate. Guíate con el ejemplo.
C
A
Validación
AT
En el diagrama siguiente completa los espacios que faltan.
En un triángulo obtusángulo, el ortocentro
queda fuera del triángulo; en un triángulo
acutángulo, el ortocentro queda dentro
del triángulo, y en un
triángulo rectángulo, el
ortocentro es uno de sus
vértices.
En un triángulo acutángulo; el circuncentro
queda dentro del triángulo, en un triángulo
rectángulo el circuncentro queda en el triángulo,
y en un triángulo obtusángulo el circuncentro
queda fuera de él.
Las medianas de un
triángulo lo dividen
en seis triángulos con
la misma área. Esta
característica le da al
baricentro el nombre de
gravicentro o centro
de masa.
Lo anterior lo
La circunferencia circunscrita
Para localizar el
circunferencia que
cumple una
que pasa por los tres vértices
circuncentro se
pase por los puntos
A, B, y C del triángulo
circunferencia
circunscrita
del triángulo tiene su centro
en el circuncentro del
trazan las
mediatrices
es necesario que la
al triángulo.
triángulo.
M
Para trazar una
.
distancia del centro
de la circunferencia
a cada vértice sea
la misma
34
SACMA1WB_B1.indd 34
.
Se traza una circunferencia cuyo centro se ubica en el circuncentro del triángulo y
vértices
además pase por los del triángulo.
Contenido: Trazo y análisis de las propiedades de las alturas, medianas, mediatrices y bisectrices en un triángulo.
25/01/13 20:21
Problemas de reparto proporcional
N
sentido numérico y
pensamiento algebraico
El reparto proporcional es un procedimiento mediante el cual una cantidad se divide en
partes proporcionales considerando determinados aspectos para que el reparto sea más
justo o cumpla ciertos criterios. El reparto proporcional se utiliza en distintos campos, como
en el área laboral, donde se aplica en el reparto de utilidades, aguinaldos, gratificaciones o
prestaciones, donde además del número de empleados de una empresa se consideran aspectos como antigüedad, puntualidad, eficiencia, puesto de trabajo, etcétera.
Desafío matemático
La razón entre dos cantidades es el cociente,
que resulta de dividir
una de ellas entre la otra.
Cuando la razón entre
dos cantidades es igual
a la razón entre otras
dos, se dice que éstas
son proporcionales. Por
ejemplo,
M
O
forma, espacio y medida
C
Tres amigas compraron un boleto para una rifa y ganaron un premio de
$5 000.00. El precio total del boleto fue de $40.00, de los cuales Yolanda aportó
$12.00, Zenaida $8.00 y Ximena el resto. Si el premio se reparte de manera proporcional a lo que aportaron para comprar el boleto, ¿cuánto le corresponde a
cada una?
Le corresponden a Yolanda $1 500.00, a Zenaida $1 000.00
IO
Conceptos clave
PR
O
y a Ximena $2 500.00.
Las claves del problema
E
3
6
= 1.5 =
.
2
4
$8.00
D
$20.00
proporcionales ya que
manejo de la información
1. Elige la opción correcta.
a)¿Cuánto aportó Ximena?
$40.00
$12.00
3
6
y
son
2
4
2
20
12
IA
4
L
b)¿Qué fracción representa la cantidad que aportó Ximena respecto al
total del costo del boleto?
1
1
1 1
ER
c)Si el reparto del premio debe ser proporcional a lo que cada una
aportó, ¿cuánto le corresponde a Ximena?
$1 500.00
$2 000.00
$2 500.00
$5 000.00
AT
d)¿Qué fracción del costo del boleto aportaron respectivamente Yolanda y Zenaida?
1
3
1
1
y 1
y 1
y 1 y 1
8
10
5
40
20
M
12
e)¿Qué fracción del premio les corresponde?
1 y 1
3 y 1
1 y 1 12
8
10
5
40
20
3
4
1 y 1
3 4
f) Por tanto, ¿qué cantidad del premio le corresponde a Yolanda y a
Zenaida?
$416.66 y $625.00
$1 500.00 y $1 000.00
$125.00 y $250.00
$1 250.00 y $1 250.00
Contenido: Resolución de problemas de reparto proporcional.
SACMA1WB_B1.indd 35
35
25/01/13 20:21
1. Dos personas compraron 40 dulces y pagaron $20.00 en total. Si una de ellas aportó
$13.00, y la otra, $7.00, ¿es justo que se repartan equitativamente los dulces, es decir,
que a cada uno le toquen 20? ¿Por qué?
No es justo porque no aportaron la misma cantidad de dinero.
26 dulces a la que aportó $13.00 y 14 dulces a la que aportó $7.00.
O
A Miguel $1 160.00, a Javier $696.00 y a Vicente $464.00.
M
O
C
2. En un concurso de tiro al blanco con dardos Miguel obtuvo el primer
lugar, Javier el segundo y Vicente el tercero. Al primer lugar le corresponde la mitad del premio, al segundo 3 y al tercero 1 . Si el premio
10
5
total es de $2 320.00, ¿cuánto le corresponde a cada uno?
D
E
PR
3. Daniel y Pablo recibieron $6 000.00 por construir una barda. Daniel trabajó seis días y Pablo nueve. Si el pago es proporcional al número de
días trabajados, ¿cuánto recibe cada uno?
Daniel recibe $2 400.00 y Pablo recibe $3 600.00.
IA
L
4. Don Carlos repartió su herencia de $859 500.00 entre sus únicos dos
familiares. Si su sobrino recibió dos terceras partes de lo que recibió su
hermano, ¿cuánto recibirá cada uno?
El Sobrino recibirá $343 800.00 y su hermano
recibirá $515 700.00.
ER
forma, espacio y medida
manejo de la información
N
a) ¿Cómo sugieres hacer el reparto?
IO
sentidonumérico
numéricoyy
sentido
pensamientoalgebraico
algebraico
pensamiento
Ahora practica
M
AT
5. Se quiere dividir en dos lotes un terreno de 8 925 m2, de manera que el
área del menor sea tres cuartas partes la del lote mayor. ¿Cuánto deben
medir los lotes?
Un lote debe medir 5 100 m2 y el otro 3 825 m2.
6. La tía Consuelo dispone de $437.50 para repartir entre sus tres sobrinas
de 9, 11 y 15 años, respectivamente. Si la repartición se hace de acuerdo
con sus edades, ¿cuánto recibirá cada una?
La sobrina de 9 años recibirá $112.50, la de 11 años recibirá $137.50
Conceptos clave
La razón entre dos
cantidades es el cociente
que resulta de dividir
una entre otra. Cuando
la razón entre dos cantidades es igual a la razón
entre otras dos, se dice
que éstas son proporcionales; por ejemplo,
3
6
y
son
2
4
proporcionales, ya que
3
6
= 1.5 =
.
2
4
En un reparto proporcional, cuando la
relación es de proporcionalidad directa, si
una cantidad aumenta,
entonces la otra aumenta en la misma proporción. Y viceversa: si una
cantidad disminuye, entonces la otra disminuye
en la misma proporción.
Por ejemplo, se repartieron $10.00 entre dos
personas: una recibió
$6.00 y la otra, $4.00. Si
se repartirá el doble, es
decir, $20, entre las dos
personas y en la misma
proporción, recibirían el
doble: la primera $12.00
y la segunda $8.00.
y la de 15 años recibirá $187.50.
36
SACMA1WB_B1.indd 36
Contenido: Resolución de problemas de reparto proporcional.
25/01/13 20:21
sentido numérico y
pensamiento algebraico
7. Pedro, Paco y Luis invirtieron, respectivamente, $5 000.00, $7 000.00 y $9 000.00
en un negocio de videojuegos y, al cabo del un año, tienen una ganancia de
$84 000.00. Si las ganancias se reparten proporcionalmente a la cantidad invertida,
¿cuánto le corresponde a cada uno?
A Pedro le corresponden $20 000.00, a Paco $28 000.00 y a Luis $36 000.00.
Una manera de resolver un problema de
reparto proporcional
es encontrar la cantidad
que corresponde a una
unidad; por ejemplo,
en el problema 1 al
dividir el total de dulces
entre el costo se obtiene
la cantidad que corresponde a cada peso
aportado; es decir,
M
O
2 100 m2 a cada uno.
forma, espacio y medida
C
IO
N
8. Tres hermanos cooperan para comprar un terrero de 7 000 m2; el mayor aporta dos
quintas partes de su costo y los otros dos hermanos el resto, dividido en partes
iguales. ¿Qué superficie del terreno les corresponde si la repartición se
hace de manera proporcional a la inversión de cada uno?
Al mayor le corresponden 2 800m2 y a los otros dos hermanos
Conceptos clave
IA
L
D
10. Para abrir un negocio cuatro personas aportaron $500.00, $700.00,
$1 100.00 y $1 600.00, respectivamente, y acordaron repartir las ganancias proporcionalmente a la inversión inicial de cada uno. Si después
de dos meses el que invirtió menor capital ganó $2 500.00, ¿cuánto
obtuvieron los otros tres?
El que aportó $700.00 ganó $3 500.00, el que aportó $1 100.00
ER
ganó $5 500.00 y el que aportó $1 600.00 ganó $8 000.00.
M
AT
11. Una empresa repartió una gratificación de $60 000.00 entre cuatro empleados de manera proporcional a la antigüedad laboral de cada uno.
Dos de los empleados tienen una antigüedad de 25 años y los otros
dos obtuvieron $15 000.00 y $7 500.00, respectivamente. ¿Cuánto recibieron los empleados con 25 años de antigüedad? ¿Cuántos años de
antigüedad tienen los otros dos?
Los empleados con 25 años de antigüedad recibieron $18 750.00,
40
= 2, por lo que
20
manejo de la información
E
PR
O
9. Elena, Miguel y Mariano invirtieron $20.00, $50.00 y $90.00, respectivamente, para un puesto de dulces típicos en la kermés. Si Miguel tiene una ganancia de $90.00 y la de todos fue en la misma proporción,
¿cuánto ganaron Elena y Mariano?
Elena ganó $36.00 y Mariano $162.00.
corresponden 2 dulces
por cada peso.
Otra forma de
resolver problemas
de reparto proporcional es hallar la fracción
del total que le corresponde a cada parte
entre las que se hace el
reparto; por ejemplo:
se pagaron $1 200.00
por un trabajo de seis
días, de los cuales Karla
trabajó dos y Mariana
cuatro, y se repartieron
el dinero de manera
proporcional a los días
trabajados. Karla trabajó
dos días de seis, por lo
que le corresponden dos
sextas partes del pago
total, y a Mariana cuatro
sextas partes.
el empleado que recibió $15 000.00 tiene 20 años de antigüedad
y el empleado que recibió $7 500.00 tiene 1 año de antigüedad.
Contenido: Resolución de problemas de reparto proporcional.
SACMA1WB_B1.indd 37
37
25/01/13 20:21
César
Angélica
Leonor
Fabián
Total
Cantidad de árboles
1 000
500
250
1 000
250
3 000
Cantidad invertida ($)
500
250
125
500
125
1 500
N
Reyna
IO
sentidonumérico
numéricoyy
sentido
pensamientoalgebraico
algebraico
pensamiento
12. Reyna, César, Angélica, Leonor y Fabián compraron 3 000 árboles para reforestar.
Por ellos pagaron $1 500.00 en total y dividieron los árboles de manera proporcional a la cantidad de dinero aportada por cada uno. A partir de los datos anteriores
completa la siguiente tabla.
C
No, porque no aportaron la misma cantidad de dinero.
O
a)¿Qué proporciones utilizaste para dividir el premio? ¿Cómo las obtuviste?
Con
una regla de tres con el precio del boleto y el premio obtuve la
E
parte
que correspondía a cada quién.
IA
L
D
2. Resuelve el problema.
a)Ximena, Yolanda y Zenaida utilizaron la mitad del premio que ganaron para preparar ensaladas y venderlas. Si obtuvieron una ganancia total de $450.00, ¿cuánto
le corresponde a cada una si reparten las ganancias de manera proporcional a la
inversión?
Yolanda obtuvo $135.00, Zenaida $90.00 y Ximena $225.00.
ER
manejo de la información
M
O
1. ¿Si en el problema planteado en el Desafío matemático el premio se hubiera dividido
equitativamente, el reparto habría sido justo? ¿Por qué?
PR
forma, espacio y medida
Regreso al Desafío matemático
AT
Validación
M
1. En el diagrama siguiente, escribe sobre las líneas las palabras que faltan
para completar los enunciados.
Yolanda es
de Zenaida,
Para saber qué fracción
Ya que se trata de un
representa la cantidad
reparto proporcional,
y el boleto costó $40;
anterior respecto al total
20
basta dividir la fracción del premio
entonces Ximena puso
$20.00 .
entre 40
entonces
la fracción es SACMA1WB_B1.indd 38
corresponde a 3
y la
Entre Yolanda y Zenaida
aportaron $20.00
38
La fracción que le
;
1
2
que le corresponde
a Ximena es
la misma que la
.
1
anterior, es decir 2 .
10
1
5
,
.
Por tanto, las cantidades
que les corresponden
son: Yolanda, $1 500.00 ,
Zenaida, $1 000.00 y
Ximena, $2 500.00 .
Contenido: Resolución de problemas de reparto proporcional.
25/01/13 20:21
Juegos de azar y elección de estrategias
N
sentido numérico y
pensamiento algebraico
Existen diversas situaciones en las que no es posible saber con certeza lo que sucederá,
como en los juegos de azar y los experimentos aleatorios, escenarios en los que los resultados no los determinan las habilidades de los participantes, sino la casualidad. Sin embargo,
es posible hacer predicciones respecto a los resultados con base en los resultados posibles;
por ejemplo, al lanzar una moneda al aire no podemos determinar el resultado: águila o sol,
pero sí tener la certeza de que será alguno de los dos.
IO
Desafío matemático
M
O
forma, espacio y medida
C
Andrea, José y Santiago juegan a lanzar dos dados y sumar los puntos de sus caras superiores. José dice que 7 será la suma más frecuente, pero Andrea está segura de que al sumar los
dados el 9 aparecerá más veces porque es su número de la suerte. Santiago piensa que todos
los números, del 2 al 12, tienen la misma posibilidad. ¿Cómo determinarías quién tiene razón?
Hay que encontrar todas las combinaciones posibles y ver cuál es la más probable,
O
dado que cada combinación tiene la misma posibilidad de ocurrir. En este caso,
PR
el 7 es el número que tiene mas combinaciones, por lo tanto es el más probable.
Las claves del problema
E
11
manejo de la información
a) ¿Cuáles son los resultados posibles al tirar un dado?
6
12
2
IA
L
D
b) Al tirar dos dados y sumar los puntos de sus caras superiores:
• ¿Cuáles son las sumas que se pueden obtener?
Del 1 al 6
Del 6 al 12
Del 2 al 12
Del 1 al 12
ER
• ¿De cuántas maneras distintas se puede obtener como suma el número 12?
De 1 manera
De 2 maneras
De 4 maneras De 12 maneras
De 12 maneras
AT
• ¿Y de cuántas se puede obtener el número 4?
De 1 manera
De 3 maneras
De 6 maneras
M
• En la suma de las tiradas de dos dados ¿Todos los números tienen la misma posibilidad
de salir?
No, porque las combinaciones posibles son distintas para cada suma.
Sí, porque es un juego de azar y no es posible suponer el resultado.
Sí, porque depende de la suerte de quien lanza los dados.
No, porque no todas las personas tienen la misma suerte.
Contenido: Identificación y práctica de juegos de azar sencillos y registro de los resultados. Elección de estrategias en
función del análisis de resultados posibles.
SACMA1WB_B1.indd 39
39
25/01/13 20:21
1. Analiza las siguientes situaciones y subraya las que determina el azar.
• Lotería
• Futbol
• Tirar un dado
• Tirar dos dados
• Tiro al blanco con dardos
• Matatena
• Ruleta
• Voleibol
• Ajedrez
• Póquer
• Balero
• Rifa
N
2. Lanza una moneda nueve veces y registra cada resultado en la siguiente tabla. Puedes utilizar la letra A para “águila” y S para “sol”.
Respuesta variable.
Número de lanzamiento
1
2
3
4
5
6
7
Resultado
8
9
M
O
forma, espacio y medida
C
a) ¿Este juego es azar o depende de la habilidad de los participantes? ¿Por qué?
Es un juego de azar, en el que no se puede controlar el resultado.
O
b)¿Qué resultado se obtuvo más veces? Respuesta variable
c) ¿Si haces nuevamente nueve lanzamientos la respuesta anterior será la misma?
PR
No necesariamente. Al ser un juego de azar, el resultado puede cambiar
o puede repetirse cada vez.
D
E
3. Haz en tu cuaderno una tabla como la anterior y lanza de nuevo una moneda nueve
veces para completarla.
L
a) ¿El resultado que salió más veces es el mismo que el del inciso b de la actividad anterior? ¿A qué se debe?
IA
No necesariamente. Al ser un juego de azar, el resultado puede cambiar
o puede repetirse cada vez.
ER
manejo de la información
IO
sentidonumérico
numéricoyy
sentido
pensamientoalgebraico
algebraico
pensamiento
Ahora practica
M
AT
4. Lanza dos monedas a la vez once veces y registra los resultados en la siguiente tabla.
Utiliza nuevamente las letras A y S para representarlos. Luego haz en tu cuaderno
dos tablas iguales y realiza los lanzamientos necesarios para completarlas.
Número de lanzamiento
1
2
3
4
5
6
7
8
9
10
11
Resultado
Los resultados de este ejercicio son aleatorios.
a) ¿Cuál o cuáles fueron las combinaciones de resultados que salieron más veces en cada
tabla?
Tabla 1: Tabla 2: Tabla 3: 40
SACMA1WB_B1.indd 40
Contenido: Identificación y práctica de juegos de azar sencillos y registro de los resultados. Elección de estrategias en
función del análisis de resultados posibles.
25/01/13 20:21
b)¿Piensas que alguna combinación tiene más posibilidades de obtenerse que las demás? ¿Por qué?
sentido numérico y
pensamiento algebraico
Es más probable obtener una combinación águila - sol que dos caras iguales, pues
hay más combinaciones que den ese resultaso.
N
5. Completa las siguientes tablas que muestran los resultados posibles al lanzar una
y dos monedas. Guíate por los ejemplos y observa que para el lanzamiento de dos
monedas se considera el resultado individual de cada una.
Resultados posibles al lanzar una moneda
IO
Resultados posibles al lanzar una moneda
Moneda 1
Moneda 2
Resultado
Sol
sol
águila
águila
águila-águila
águila
águila
sol
sol
sol-sol
sol
águila-sol
águila
águila-sol
O
sol
M
O
águila
C
Resultado
forma, espacio y medida
Moneda
a) ¿Cuántos resultados diferentes es posible obtener al lanzar una moneda?
b)¿Cuántos al lanzar dos?
PR
Una
Tres
D
E
manejo de la información
c) Subraya la combinación que supones tiene más posibilidades de salir al lanzar dos
monedas a la vez. Justifica tu respuesta.
• Dos soles
• Un águila y un sol
• Dos águilas
1
L
La
posibilidad de que salga un águila y un sol es de 2 ,
1
IA
mientras
que la posibilidad de dos soles o dos águilas es sólo 4 .
ER
d)Si en un lanzamiento de dos monedas tuvieras que elegir un resultado para ganar, ¿qué
combinación escogerías? ¿Por qué?
Un águila y un sol, por ser el más probable.
AT
M
6. En una urna hay 10 canicas del mismo peso y tamaño, y de los siguientes colores:
tres amarillas, dos verdes, dos negras y una azul. Una de ellas se extrae al azar.
a) Si quieres predecir de qué color es, ¿cuál te conviene elegir para tener más posibilidades de acertar? ¿Por qué? La amarilla, porque hay más canicas de ese color en la urna.
b)¿De qué color es la canica con menos posibilidades de salir? Justifica tu respuesta.
La azul, pues solo hay una en la urna.
Contenido: Identificación y práctica de juegos de azar sencillos y registro de los resultados. Elección de estrategias en
función del análisis de resultados posibles.
SACMA1WB_B1.indd 41
41
25/01/13 20:22
Número de
lanzamiento
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19 20
Suma
obtenida
b)Si el experimento se repite, ¿el resultado será el mismo? ¿Por qué? Es probable que
N
sentidonumérico
numéricoyy
sentido
pensamientoalgebraico
algebraico
pensamiento
7. Lanza dos dados 20 veces y en la siguiente tabla, para cada lanzamiento, anota la
suma de los puntos de sus caras superiores.
a) ¿Qué resultado salió más veces? R. L. Lo más probable es que sea el 7.
IO
se
repita el 7, por ser el que tiene mayor número de posibilidades de salir, pero no siempre lo hará.
C
M
O
En algunas ferias o kermeses hay juegos de apuestas con dos dados en los que también se
suman los números que salen, pero no se permite apostar al 7 o se paga el doble a quienes
apuestan al 2 o al 12. ¿Por qué existen esas reglas?
O
Porque
el 7 es el número más probable y el 2 y el 12 son los menos probables.
Así
que se paga más a los números que tienen menos combinaciones.
Si en un juego como ese tuvieras que apostar por algún número, ¿cuál elegirías? ¿Por qué?
PR
forma, espacio y medida
Regreso al Desafío matemático
Depende
de la proporción entre las posibilidades de que un número salga
E
D
Validación
L
1. Haz en tu cuaderno una tabla con las siguientes columnas y con tantas filas como sea
necesario para considerar todos los resultados posibles.
IA
Resultados posibles al lanzar dos dados y sumar los puntos de sus caras superiores
Dado 1
Dado 2
Dado 3
ER
manejo de la información
y cuanto se pague en la apuesta.
M
AT
2. A partir de la tabla anterior responde las siguientes preguntas completando con la
opción correcta los espacios vacíos.
cuatro
a)El número 9 se puede obtener de maneras distintas.
[cuatro / seis]
seis
b)El número 7 se puede obtener de maneras distintas.
[cinco / seis]
7
c)El resultado que se repite más veces es el número .
[ 7 / 9]
José
d)Entonces, es quien tiene razón porque hay más posibilidades de obtener
el número que dijo.
[Andrea / Santiago / José]
.
[todos los números tienen la misma
posibilidad / hay más posibilidades de
obtener el número que dijo.]
42
SACMA1WB_B1.indd 42
Contenido: Identificación y práctica de juegos de azar sencillos y registro de los resultados. Elección de estrategias en
función del análisis de resultados posibles.
25/01/13 20:22
Lo que aprendí
154
9 a su forma decimal.
17
17.111
3. Convierte el número 73.231 3 a su forma de fracción.
732 313
732 313
732 313
10 000
1 000
0.46
3
5
A = 3 y B = 0.43
A = 4.3 y B = 3
10
1
O
3
10
PR
A = 0.43 y B = 3 A
M
O
4. Analiza la recta numérica e indica cuánto valen A y B.
B
10
1
732 313
100
C
100 000
IO
2. Convierte, sin utilizar calculadora, la fracción
1.71
17.1
N
Marca la respuesta correcta.
1 532
1. Convierte, sin utilizar calculadora, la fracción 10 000 a su forma decimal.
15.32
1.532
0.153 2
0.015 32
A = 3 y B = 4.3
1
1
4
D
8
E
5. Rodrigo compró 1 2 kg de almendras, de los que dio 8 kg a su hermana, 4 kg a su
1
mamá y 4 kg a su papá. ¿Cuántos kilogramos de almendra le quedaron?
7 kg
3 kg
1 kg
1 1 kg
8
IA
L
6. La diferencia entre términos consecutivos de una sucesión es siempre 4. Si la sucesión empieza en el número 6, ¿cuáles son sus primeros cinco términos?
6, 10, 13, 18 y 22
6, 10, 14, 18 y 22
6, 10, 15, 18 y 22
6, 10, 14, 19 y 22
ER
7. ¿Cuál de las siguientes expresiones no representa el perímetro de un cuadrado?
4 × m
4k
s + s + s + s
t×t
M
AT
8. Indica con qué herramientas de tu juego de geometría será más fácil y preciso trazar
un triángulo cuyos lados midan 2 cm, 4 cm y 5 cm.
Escuadras de 30° y 45°
Regla sin graduar y compás
Regla graduada y compás
Regla graduada y escuadra de 45°
9. Selecciona el triángulo en el que se trazaron una de sus alturas y una bisectriz.
43
SACMA1WB_B1.indd 43
25/01/13 20:22
Lo que aprendí
IO
N
10. A Javier y a Eduardo los contrataron para hacer un mueble. Javier trabajó cuatro
horas diarias durante cinco días y Eduardo tres horas diarias por seis días. Si por
el trabajo les pagaron $7 600 y los repartieron de manera proporcional al trabajo
realizado, ¿cuánto ganó cada uno?
Javier $3 800 y Eduardo $3 800
Javier $4 000 y Eduardo $3 600
Javier $3 600 y Eduardo $4 000 Javier $3 100 y Eduardo $4 500
M
O
C
11. Tres hermanos compraron un paquete de 36 latas de jugo y pagaron $198.
El primero colaboró con la mitad del costo total, el segundo aportó $44, y el
tercero, el resto. Si el reparto lo hicieron de manera proporcional al dinero que
cada uno aportó, ¿cuántas latas de jugo le corresponden al tercer hermano?
10 latas
18 latas
8 latas
12 latas
O
12. Selecciona la opción que corresponde a un juego de azar.
Futbol
Ajedrez
Damas chinas
PR
13. Selecciona la opción que no corresponde a un juego de azar.
Lotería
Basquetbol
Serpientes y escaleras
Ruleta
Oca
M
AT
ER
IA
L
D
E
14. Al lanzar tres monedas al aire, ¿con cuál de las siguientes opciones sería más probable ganar?
Que al caer las tres caras superiores fueran sol.
Que al caer las tres caras superiores fueran águila.
Que dos caras sean sol y la otra águila.
Que al caer al menos una de las caras superiores fuera águila.
44
SACMA1WB_B1.indd 44
25/01/13 20:22