TECNICAS OPERATIVAS PARA EL CONTROL DE GESTION DE LA

TECNICAS OPERATIVAS PARA EL CONTROL DE GESTION DE LA LIQUIDEZ
1
EN ENTORNOS DE CERTIDUMBRE, ALEATORIEDAD E INCERTIDUMBRE
Prof. Dr. D. Enrique López González
Departamento de Dirección y Economía de la Empresa
Universidad de León
"En lugar de una teoría económica entre otras muchas que existen,
propondremos un trabajo mucho más modesto: emplear de la mejor
manera posible las informaciones disponibles para construir
modelos matemáticos intentando engañarnos lo menos posible...
a nosotros mismos".
A. Kaufmann and J. Gil Aluja
(Técnicas operativas de gestión para el tratamiento de la
incertidumbre, 1987)
I. Introducción
Una de las principales cuestiones del control de gestión es aquella referida a la toma de
decisiones que afecta a los flujos monetarios y, en definitiva a los resultados financieros de las
empresas. De hecho se presentan tres problemas principales: primero, no manterner saldos de
liquidez ociosos, es decir, produciendo una rentabilidad por debajo de una alternativa mejor
conseguible; segundo, no financiar descubiertos a tasas más altas que otras posibles; y tercero,
evitar que de forma simultánea se esté utilizando una línea de financiación a tipo alto y se
tengan recursos excedentes a tipos menores.
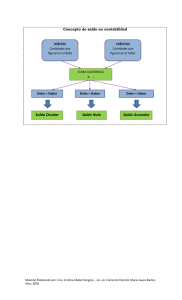
En la Figura 1 se ilustra un sistema típico de gestión de la liquidez. Diariamente pueden
tener lugar flujos monetarios positivos y negativos. En cuanto a los primeros, pueden servir para
cubrir los segundos cuando éstos se produzcan, pero puede existir un periodo de tiempo entre
unos y otros en el cual sería absurdo mantener saldos de caja ociosos, tal como se mencionó
anteriormente. En este sistema hay dos costes relevantes a considerar: (1) el coste de
oportunidad (osea la pérdida de réditos) por mantener valores en efectivo en lugar de tenerlos en
la cartera de valores y (2) el coste de transacción que ocurre al mudar valores de la cartera a la
caja o viceversa y que están relacionados con las comisiones percibidas por el agente o corredor
que en último término realiza la operación de compra-venta.
(1) Estudio basado en el Trabajo "An Application of The Kaufmann and Gil Aluja Fuzzy Chains to Management Control:
Fuzzy Cash Management", presentado con la colaboración de la Profesora D Cristina Mendaña Cuervo a SECOND
CONFERENCE OF THE BALKANIC UNION FOR FUZZY SYSTEMS AND ARTIFICIAL INTELLIGENCE. (31
August-5 September 1992). Trabzon, Turkey (Investigación financiada con una Ayuda de la Junta de Castilla y León, P.I.
n 1402/90).
Figura 1. Sistema de gestión de la liquidez.
En consecuencia, la gestión de la liquidez supone la resolución de dos cuestiones
interdependientes: la fijación del nivel óptimo de liquidez y la determinación de la periodicidad
y montante de las transferencias entre la caja y la cartera de inversiones (activos líquidos).
A este respecto, nuestro estudio comenzará por la situación donde se conoce el
comportamiento exácto de los flujos de caja como primer paso del proceso secuencial que nos
acerque a otros planteamientos más cercanos a la realidad. De esta forma, la presente disertación
se divide en dos partes principales. En la primera se estudiaran las técnicas más usuales para la
resolución de los problemas mencionados y se plantea el interés de la aplicación de las cadenas
de Markov cuando se consideran los flujos de caja como una variable aleatoria.
Sin embargo, existen situaciones en que no es posible utilizar probabilidades, cuando existe
incertidumbre en lugar de aleatoriedad. Si nuestro conocimiento del entorno es impreciso, como
puede ocurrir en la toma de decisiones de gestión de la liquidez, el modelo debe incluir la
noción de cadenas con datos borrosos, en lugar de probabilidades, recientemente desarrollada
por KAUFMANN y GIL ALUJA (1991). De esta forma, en la segunda parte, el objetivo de
nuestro estudio consiste en examinar las cadenas inciertas (relaciones borrosas normales),
desarrolladas por los profesores mencionados, como instrumentos operativos válidos para
evaluar sistemas de gestión de la liquidez.
II. Técnicas operativas para el control de gestión de la liquidez en ambiente de certeza y
de aletoriedad
Las técnicas más usuales de gestión de la liquidez están basadas en su mayoría en los
modelos de control de inventarios (stocks) y solamente presentan diferencias significativas en
cuanto a la distinta consideración del comportamiento de los flujos de caja: por un lado, se
encuentran aquellos modelos, como por ejemplo los desarrollados por BAUMOL (1952) y
BERANEK (1975), que asumen un ambiente de certeza y, por otro lado, están los modelos
probabilísticos, como por ejemplo los de PATINKIN (1956) y MILLER y ORR (1966), donde
se considera que los cash-flows se comportan como una variable aleatoria, aunque, como los
anteriores, también se interesan especialmente por fijar la cuantía óptima del saldo de caja.
No obstante, a efectos de determinar la periodicidad y montante de las transacciones entre la
caja y la cartera de inversiones puede presentar interés comprobar la aplicación de las cadenas
de Markov cuando se consideran a los flujos de tesoreria como una variable aleatoria.
II.1. La gestión de la liquidez en ambiente de certidumbre
Uno de los modelos más conocidos de gestión de la liquidez en condiciones de "previsión
perfecta" o ante certidumbre es el modelo de BAUMOL (1952), según el cual los saldos de caja
evolucionan en la forma descrita en la Figura 2. Ello quiere decir que las entradas de caja se
producen instantáneamente, por ejemplo un día, mientras que las salidas se efectúan
regularmente a lo largo del tiempo.
Figura 2. Perfil de evolución del saldo de caja según el modelo de Baumol.
Supongamos que estamos situados en el momento t0. De acuerdo con la Figura 2, el saldo
inicial de caja es T, una parte de ese saldo, R, es retenido en caja por razones de precaución y el
resto, I, es invertido en valores liquidables que ofrecen un rendimiento financiero de i. En
principio, R es suficiente para cubrir los pagos del periodo que va desde t0 a t1, una semana si el
ciclo de cobros es mensual. En t1 se venderán c pesetas de valores liquidables que ingresarán en
caja y servirán para cubrir los pagos correspondientes al periodo entre t1 y t2. De igual manera, c
pesetas de valores serán transformadas en caja en t2 y t3. Al término del ciclo, es decir, en t4,
ingresarán en caja T pesetas sobre las cuáles se realizará similar asignación entre inversión y
caja iniciales.
El tiempo transcurrido entre t0 y t1 es igual a (T - I)/T, suponiendo que los desembolsos
observan una pauta regular a lo largo del ciclo. Además el saldo medio de caja en ese periodo
será, aproximadamente (T -I)/2. El coste de oportunidad propio de mantener R pesetas entre t0 y
t1 podrá ser escrito como [(T - I)/2] i [(T - I)/T], estando i expresado en tanto anual y (T - I)/T en
fracción de año. El coste de transacción asociado a la inversión en títulos de I pesetas en t0 será
igual a bd + KdI, donde bd y Kd son, respectivamente, los costes fijos y variables propios de la
operación.
Por otra parte, los costes relacionados con la gestión de caja en el resto del ciclo pueden ser
escritos de la siguiente manera:
Costes = ( c / 2 )
Saldo medio
de caja
i
(I/T)
Periodo de
tiempo desde
t1 hasta t4
= Costes de oportunidad
+
( bw
+ Kw c ) ( I / c )
Coste
Coste N de operaciones
fijo
variable
+ Costes de transacción
Sumando las dos expresiones de costes correspondientes a los periodos t0t1 y t1t4, tendremos
los costes totales propios de la gestión de caja desde t0 hasta t4, es decir, el ciclo completo de
caja.
CT =
( T - I / 2 ) i ( T - I / T ) + bd + Kd I +
+ ( c / 2 ) i ( I / T ) + ( bw + Kw c ) I / c
¡Error!Marcador no definido.
Derivando esta expresión con respecto a c, obtendremos el saldo óptimo de caja, es decir,
aquel valor que hace mínima la suma de costes de oportunidad y de transacción.
/ CT / / c =
( i I 2 T / (2T) ) + ( - b
2
w
2
I/c
)=
2
=
i I / 2 T - bw I / c = 0
2
c = bw I 2 T / i I
c=
2 bw T / i
A pesar del atractivo del modelo, el carácter restrictivo de las hipótesis de partida hace que
sólo sea aplicable en un número limitado de casos. En efecto, la mayor parte de las empresas
registran entradas y salidas de caja a lo largo del tiempo que no observan el ritmo regular
presumido por el modelo, de ahí que la hipótesis de certeza no sea admisible en una buena parte
de los casos lo que otorga al mismo un margen reducido de operacionalidad.
II.2. La gestión de la liquidez en ambiente aleatorio: cadenas de Markov
Uno de los primeros modelos donde se considera que los cash-flows se comportan como
una variable aleatoria es el ideado por MILLER and ORR (1966) cuyo propósito consiste en
establecer unos niveles límite de caja tales que sirvan de guía para el responsable de la gestión
de liquidez. No obstante, el problema central, como en el caso anterior, reside en fijar la cuantía
óptima del saldo de caja, de forma que la tasa de rentabilidad sobre la inversión sea máxima.
Los límites superior e inferior de control del saldo de caja, tal como se muestra en la Figura 3,
son X e Y, mientras que Z designa el saldo de caja considerado como objetivo a alcanzar. De
esta forma, cuando el saldo de caja alcanza un nivel X, entonces se deben invertir (X - Z)
unidades monetarias en valores; cuando el saldo desciende hasta Y, es preciso vender (Z - Y)
unidades monetarias de valores o activos líquidos obteniéndose así la suma de dinero
correspondiente. Como indica la Figura 3, la transacción es instantánea.
Figura 3. Perfil de evolución del saldo de caja según el modelo de Miller y Orr.
La expresión matemática, fruto de las consideraciones anteriores, es la siguiente:
Z =
3
2
3b 1 /4i
+Y
en donde,
b = Coste fijo por conversión de valores en dinero, y viceversa.
1 = Desviación típica de las variaciones diarias del saldo de caja
i = Tasa diaria de rendimiento de los valores que pueden ser objeto de inversión.
Sin embargo, este modelo no llega a resolver la determinación de cuándo y por cuánto deben
realizarse las transferencias entre caja y cartera de valores. En otras palabras, al controller le
interesa conocer, qué probabilidad habrá para vender valores de la cartera de inversiones, por
ejemplo, dos días después de haber inspeccionado el estado del saldo de caja. Esta pregunta es
de su incumbencia ya que según donde se encuentre el saldo de caja deberá o no vender valores
para obtener efectivo y, así, planificar cuáles serán los valores de su cartera que deberá vender.
Para resolver la cuestión anterior nos puede ser útil la noción de cadena de Markov que es un
modelo de proceso aleatorio en el transcurso del tiempo y cuya característica fundamental es
ésta: la probabilidad de que el sistema bajo estudio esté en una condición particular depende
sólo de su condición actual.
Podemos construir entonces el modelo considerado arriba para el problema del control de
gestión de la liquidez mediante una cadena de Markov; para ello, supongamos un sistema S que
puede tomar N estados E1, E2,...., EN (N finito). Se admite que es posible medir o calcular la
probabilidad de ocurrencia de que S esté en el Estado Ei, i = 1,2,...N y esto para todos los
momentos en tiempo discreto n = 0,1,2,3,... y se escribe para estas probabilidades pi(n), i =
1,2,...N, n = 0,1,2,3.... Las pi(n) forman los elementos del conjunto de "vectores de estado" que
describen el sistema para todos los momentos del futuro considerados, esto es, la probalidad de
que el sistema se encuentre en el estado Ei en la fecha n.
[p(n)] =
E1
E2
p1 (n)
p2 (n)
EN
.....
pN (n)
(1)
Se establece la hipótesis de que el paso de un estado Ei a un estado Ej sólo depende de Ei y de
Ej. Se supone que es posible medir o calcular la probabilidad de todo par (Ei, Ej), i,j = 1,2....N,
que llamaremos pij sabiendo que el sistema se hallará en el estado Ej en el momento n+1 y está
en el estado Ei en el momento n. Se establecen entonces como ecuaciones que rigen el sistema:
N
pj (n+1) =
p (n) # p
i
j = 1, 2,...N
ij
(2)
i=1
Se supone aquí que las pij no dependen de n (cadena estacionaria). Podemos representar (2)
también bajo la forma matricial:
%
E1
E2
p1 (n+1)
p2 (n+1)
EN
......
pN (n+1)
=
E1
E2
EN
p1 (n)
p2 (n)
....
E1
E2
E1
p11
p12
...
p1N
E2
p21
p22
...
p2N
:
:
:
%
pN (n)
EN
.
..
:
(3)
EN
pN1
pN2
...
pNN
en donde % significa la composición "suma-producto" (filas por columnas).
Se puede escribir también de forma simplificada:
[p(n+1)] = [p(n)] % [ M ]
(4)
La matriz de transición formada por las probabilidades pij, y que se designa por [ M ] se
llamará "matriz estocástica" y poseerá las propiedades que se señalan a continuación:
pi(n) 0,
j = 1,2,...N
n = 0,1,2,3,...
(5)
N
p (n) = 1,
n = o,1,2,3,...
(6)
pij 0,
i,j = 1,2,...N
(7)
j
j=1
N
p = 1,
i = 1,2,...N
ij
(8)
j=1
En particular, supongamos que la matriz de la Figura 4 describe el comportamiento del
balance de caja. Los números de la columna vertical (filas) son la cantidad de dinero (unidades
monetarias) en la contabilidad de caja en la mañana del día n. Los números de la fila superior
(columnas) son el balance de caja en unidades monetarias (u.m.) en la mañana del día n+1. La
tabla señala, por ejemplo, que si el balance de caja es 2 (20.000 u.m.) en el día n, será 1 (10.000
u.m.) el día n+1 con probabilidad de 0.177 (el número marcado en la fila 2, columna 1, es
0.177). De esta forma, la Figura 4 muestra la matriz de transición del proceso, basado en el
sistema de control descrito en la Figura 3, donde se supone una cota superior de 5 y una cota
inferior de 1, con el punto de retorno igual a 2. En dicha matriz las filas 2, 3 y 4 muestran los
calculos o medidas de la probabilidad de que el sistema se mueva de un estado a otro. Para
deducir las probabilidades de los estados 1 ó 5 hay que recordar que cuando el controller llega el
día n y encuentra el sistema en el estado 1 ó 5, inmediatamente lo transfiere al estado 2, de ahí
que los datos de las filas 1, 5 y 2 son los mismos.
1
2
3
4
5
1
.177
.588
.235
0
0
2
.177
.588
.235
0
0
3
0
.29
.184
.526
0
4
0
0
.324
.541
.135
5
.177
.588
.235
0
0
Figura 4. Matriz de transición del balance de caja.
La matriz estocástica de la Figura 4 es la matriz de transición de un paso para este problema,
facilitándonos conocer la probabilidad de que el sistema se mueva de un estado a otro en un
paso.
Si el sistema comienza en el estado 2, cuál es la probabilidad de que se encuentre en el
estado 3 después de dos etapas?
Estado inicial
&1
Después de un paso
Después de dos pasos
1&
&
2&
&
&2
3&
&
&3
4&
&
&4
5&
&
&5
2
2,3
p
= (0.177 x 0.235) + (0.588 x 0.235) + (0.235 x 0.184) + (0 x 0.324) +
+ (0 x 0.235) 0.223
En términos generales, si pij es la probabilidad de que el sistema vaya del estado i al estado j
2
en un paso, y p i,k es la probabilidad de que el sistema vaya de i a k en dos pasos, entonces:
2
i,k
p
= (pi,k) (pj,k)
toda j
2
Puede utilizarse esta ecuación para calcular p i,k para todas las combinaciones posibles de i y
k. Asimismo, pueden presentarse después los valores en forma matricial y se habrá construído
un Matriz de transición de dos pasos.
Para la construcción de la matriz de transición de dos pasos, podemos hacer uso de un
ejemplo sencillo. Sea
1
2
1
0.8
0.2
2
0.3
0.7
la matriz de transición de un paso.
2
1,1,
Calculemos primero p
1&
2
11
p
1
&
&
2
la probabilidad de pasar de 1 a 1 en dos pasos
&1
= p11 p11 + p12 p21 = (0.8) (0.8) + (0.2) (0.3) = 0.7
2
2
21
Para completar la matriz, evaluemos de forma similar p 12, p
2
p 12 = p11 p12 + p12 p22 = (0.8) (0.2) + (0.2) (0.7) = 0.3
2
p 21 = p21 p11 + p22 p21 = (0.3) (0.8) + (0.7) (0.3) = 0.45
2
p 22 = p22 p22 + p21 p12 = (0.7) (0.7) + (0.3) (0.2) = 0.55
Por tanto, la matriz de transición de dos pasos será:
1
2
1
0.7
0.3
2
0.45
0.55
2
y p 22:
Por otro lado, podemos observar como se puede utilizar el mismo procedimiento para
3
calcular la matriz de transición de tres pasos. Si p i,j es la probabilidad de pasar de i a j en tres
pasos, entonces:
3
i,j
p
= pi,k p
2
k,j
toda k
Podemos observar entonces que el cálculo de las probabilidades de transición de dos, tres o,
de hecho, n pasos, consiste en hacer una lista de todas las rutas, encontrar la probabilidad de
cada una y sumarlas todas. Lo cual nos lleva al concepto de multiplicación de matrices
(composición suma-producto) como base conceptual del encadenamiento markoviano.
En este sentido, cabe recordar que sólo se pueden multiplicar dos matrices si el número de
columnas de la primera es igual al número de filas de la segunda. Esto es, si A x B =E
siendo A una matriz (nxm) y B una matriz (mxr), de modo que el número de columnas de A es
igual al número de filas de B, con lo que el producto queda definido y entonces E será una
matriz (nxr). Donde el dato del renglón i, columna j de E se obtiene multiplicando el renglón i
de A por la columna j de B, término a término, y sumando los resultados.
0.8
0.2
0.8
0.2
0.64 + 0.06
0.16 + 0.14
=
0.3
0.7
0.3
0.7
0.7
0.3
0.45
0.55
=
0.24 + 0.21
0.06 + 0.49
De esta forma, para obtener la matriz de transición de dos pasos basta con multiplicar la de
un paso por sí misma; con lo cual podemos generalizarlo en forma simbólica expresando que si
n
[ M ] es la matriz de transición de un paso, la matriz de transición de n pasos será [ M ] , que
significa el producto de n factores iguales a [ M ].
La matriz de transición de n pasos facilita al controller contestar a la pregunta planteada
anteriormente, esto es, le interesa conocer la probabilidad de que el sistema esté en un estado
específico después de n transiciones. Para lo cual si en la expresión (4) hacemos n = 0,
obtenemos:
[p(1)] = [p(0)] o [ M ]
En forma semejante,
[p(2)] = [p(1)] o [ M ] y por sustitución,
2
[p(2)] = [p(1)] o [ M ] = [p(0)] o [ M ] o [ M ] = [p(0)] o [ M ]
Por lo tanto, se podrá escribir la expresión (4) como sigue:
n
[p(n)] = [p(0)] o [ M ]
(9)
en donde p(0) es el vector de probabilidades de encontrar el sistema en un estado particular en el
instante 0, esto es, cuando se inspecciona el sistema por primera vez.
En nuestro caso de aplicación, supóngase que el controller llega el lunes por la mañana y
comprueba que el sistema está en el estado 3 (30.000 u.m.) y desea saber la probabilidad de
encontrar el sistema en el estado 1 el miércoles por la mañana, pues entonces deberá vender
valores para obtener dinero y le convendrá determinar por adelantado cuáles valores de su
cartera deberá vender.
De acuerdo con la expresión (9), obtenemos
2
[p(2)] = [p(0)] % [ M ] =
=
[0 0 1 0 0]
%
.135
.518
.223
.124
0
.135
.518
.223
.124
0
.051
.224
.272
.381
.071
.024
.173
.267
.463
.073
.135
.518
.223
.124
0
=
= [.051 .224 .272 .381 .071]
Puesto que el dato de la columna 1 es 0.051, el controller sabe que la probabilidad de tener
que transferir fondos de la cartera a la caja es sólo de 0.051 con lo cual no parece prudente
dedicar mucho tiempo a determinar qué valores se venderían si hubiese necesidad de ello el
miércoles.
Por otro lado, la expresión (9) también puede utilizarse para especificar la probabilidad de
que el sistema se mueva de un estado a otro en cualquier número de transiciones si las
probabilidades de un paso no cambian con el tiempo, lo cual nos conduce a la consideración de
las probabilidades estacionarias, es decir, la propiedad ergódica en una cadena de Markov
(KAUFMANN, 1966).
n
De esta forma, si
lim [M] = [ M ]
n
donde [ M ] es una matriz estocástica sin ningún elemento nulo, se dice que el sistema es
ergódico, que posee un régimen permanente.
La matriz [ M ] que posee esta propiedad se denomina matriz ergódica. Hay una prueba en
dos partes que dice si una cadena de Markov es ergódica: (a) debe haber una probabilidad
positiva de que se pueda pasar de un estado i a otro cualquiera j si hay suficientes transiciones y
(b) debe existir al menos un estado con probabilidad positiva de que el sistema permanezca en
él después de una transición.
Si [ M ] es tal que todas sus líneas son idénticas entonces se dice que el sistema es
"completamente ergódico", y en este caso, para n suficientemente grande, el estado del sistema
no depende del estado inicial. En efecto:
n
[p(n)] = [p(0)] o [ M ]
*
lim [p(n)] = [p(0)] o [ M ]
(10)
n
= [p]
*
en donde [p] es una de las filas idénticas de [ M ].
Para calcular las probabilidades asindóticas [p] se disponen de varios métodos, uno de los
más sencillos, especialmente si se puede utilizar la opción de multiplicación de matrices
n
incluída en la mayoría de las Hojas Electrónicas de Cálculo, consiste en calcular [M] hasta que
n+1
n
[M] =[M] .
%
[M]
[M]
=
.177
.588
.235
0
0
.177
.588
.235
0
0
.177
.588
.235
0
0
.177
.588
.235
0
0
0
.29
.184
.526
0
0
.29
.184
.526
0
0
0
.324
.541
.135
0
0
.324
.541
.135
%
=
.177
.588
.235
0
0
.177
.588
.235
2
[M]
=
.135
.518
.223
.124
0
.135
.518
.223
.124
0
.051
.224
.272
.381
.071
.024
.173
.267
.463
.073
.135
.518
.223
.124
0
........
........
........
16
[M]
17
[M]
=
=
.083
.348
.248
.284
.038
.083
.348
.248
.284
.038
.083
.347
.248
.284
.038
.083
.347
.248
.284
.038
.083
.348
.248
.284
.038
.083
.347
.248
.284
.038
.083
.347
.248
.284
.038
.083
.347
.248
.284
.038
.083
.347
.248
.284
.038
.083
.347
.248
.284
.038
En nuestro caso de aplicación, tenemos
[p] = [.083 .347 .248 .284 .038]
0
0
Podemos observar que p(1) = 0.083 y como hay 260 días laborales en el año, entonces el
número de veces en las que el sistema estará en el estado 1 en dicho año será de 0,083 x 260 =
21,58 veces. Por consiguiente, "en promedio" habrá que mover valores de la cartera a la caja
21,58 veces por año y una vez cada 260/21,58 w 12 días. Un análisis similar para el estado 5
produce 0.038 x 260 = 9,88 movimientos de la caja a la cartera por año. Esta información
presenta gran interés en la planificación de la periodicidad y montante de las transacciones entre
la caja y la cartera de inversiones.
No obstante, a pesar del atractivo de la aplicación de las cadenas de Markov, conviene
recordar que para poder aplicar una probabilidad es necesario tener, en primer lugar, una
sucesión de fenómenos que se hayan repetido en unas determinadas condiciones y, en segundo
lugar, poder aplicar los resultados obtenidos sobre otro fenómeno sometido a las mismas
condiciones que las anteriores. En este sentido, existen situaciones en que no es posible utilizar
probabilidades, cuando existe incertidumbre en lugar de azar. Si nuestro conocimiento del
entorno es impreciso, como ocurre en la toma de decisiones de gestión de la liquidez, el modelo
debería incluir la noción de cadenas con datos borrosos en lugar de probabilidades.
III. Técnicas operativas para el control de gestión de la liquidez en ambiente de
incertidumbre: cadenas inciertas de Kaufmann y Gil Aluja
En un ambiente de incertidumbre el modelo debe incluir la noción de nivel de presunción,
esto es, en lugar de una ley de probabilidad se deben tomar leyes de posibilidad. Sin embargo,
existe un gran paralelismo entre la teoría de probabilidades y la de las posibilidades: en la
primera, el axioma fundamental es la aditividad en la medida; en la segunda, el axioma
fundamental es la monotonía en la inclusión para toda valuación.
A este respecto, la propuesta de KAUFMANN y GIL ALUJA (1991) está basada en la teoría
markoviana, aunque presenta modificaciones importantes al situarse en ambiente de
incertidumbre y, por consiguiente, no emplear probabilidades. Por otro lado, el encadenamiento
markoviano se realiza a través de operadores asociados suma-producto mientras que en la
incertidumbre el encadenamiento se lleva a cabo mediante operadores asociados máximomínimo.
Construyamos entonces el modelo considerado anteriormente para el problema de la gestión
de liquidez en incertidumbre mediante una "cadena incierta de Kaufmann y Gil Aluja". Para
ello, siguiendo a dichos autores, supongamos un sistema S cuyo conjunto de estados es E = {E1,
E2,... EN} (N finito). Se admite que es posible valuar en [0, 1] la posibilidad de ocurrencia de
que S se encuentre en el estado Ei, i = 0, 1, 2 ...N y esto para todas las fechas n = 0, 1, 2, 3,... y
que se designan estas posibilidades qi(n), i = 0, 1, 2,...N, n = 0, 1, 2, 3,... Las qi(n) forman los
elementos del conjunto de vectores de estado que describen el sistema para todos los momentos
futuros considerados.
[q(n)]
=
E1
E2
q1(n)
q2(n)
EN
...
qN(n)
(11)
Se establece la hipótesis que las qi(n) forman una ley de posibilidad para todo n, es decir, que
se tiene que:
N
V q (n) = 1
(12)
i
i=1
En otras palabras, por lo menos uno de los estados tiene la posibilidad 1.
Se parte también de la hipótesis que la posibilidad de paso de un estado Ei, a un estado Ej
sólo depende de Ei y de Ej. Se supone que se puede valuar la posibilidad de todo par (Ei, Ej), i,j
= 1, 2,...N, es decir, qij, sabiendo que el sistema se hallará en el estado Ej en el momento n+1 y
está en el estado Ei en el momento n. Se establece entonces como ecuación que rige el sistema:
N
qj (n+1) =
V (q (n) Y q (n)), j = 1, 2, ....N
i
(13)
j
i=1
Se supone aquí que las qij no dependen de n (cadena estacionaria).
Por otra parte:
~ i {1, 2, ... N} : } j {1, 2, ... N}
N
Vq =1
ij
(14)
i=1
Esto es, cada fila de la relación contiene por lo menos un 1.
De esta manera, las qij forman una relación borrosa normal que se va a denominar "matriz
incierta" por comparación con la "matriz estocástica". El sistema construído en base a la "matriz
incierta" se denominará "cadena incierta" (sobreentendiéndose con filas normales) para no
llamarla cadena de Markov borrosa, ya que el nombre de Markov se halla demasiado ligado a la
noción de probabilidad.
Podemos representar de nuevo la expresión (13) ahora bajo forma matricial:
=
E1
E2
q1(n+1)
q2(n+1)
E1
E2
EN
q1(n)
q2(n)
qN(n)
EN
.....
*
qN(n+1)
=
E1
E2
E1
q11
q12
...
q1N
E2
q21
q22
...
q2N
:
:
qN1
qN2
EN
EN
.
..
:
...
qNN
en donde * significa la composición maxmin (filas por columnas), o también
N (x, z) = V (N (x, y) Y N (y, z))
(16)
y
Dado que las qi(n) y qij son valuaciones, tendrá que cumplirse que:
qj(n) 0,
j = 1, 2, ... N
n = 0, 1, 2, 3,...
(17)
N
V q (n) = 1,
j
n = 0, 1, 2, 3,...
(18)
j=1
qij 0
(19)
N
V q (n) = 1,
ij
j=1
i = 1, 2,... N
(20)
(15)
Se escribirá también (15) bajo la forma simplificada:
[q(n+1)] = [q(n)] * [ N ]
(21)
en donde [ N ] es la matriz formada por las valuaciones qij introducida en (15). De esta manera [
N ] es una relación borrosa de filas normales según la terminología de la teoría de los
subconjuntos borrosos. En el supuesto de que las qij dependan del tiempo y sean qij(n) entonces
[ N(n) ] representa una cadena llamada "no estacionaria".
Podemos ampliar nuestra consideración, por el interés pedagógico que presenta, a la noción
de relaciones --borrosas normales.
Una relación --borrosa normal posee valuaciones constituídas por intervalos de confianza de
[0, 1] en lugar de estimaciones en [0, 1]. Por ello se afectará a cada transición un intervalo de
confianza:
[a1, a2] G [0, 1]
0 a1 a2 1
(22)
pero, dado que la relación es normal, existirá siempre por lo menos un 1 en cada fila.
Conviene recordar también que:
[a, a] = a
a 0 [0, 1]
[a1, a2] (Y) [b1, b2] = [a1Yb1, a2Yb2]
[a1, a2] (Z) [b1, b2] = [a1Zb1, a2Zb2]
(23)
(24)
(25)
La composición maxmin se realizará con los intervalos de confianza de la misma manera que
con los valores de [0, 1], respetando (23), (24) y (25). Los intervalos de confianza de [0, 1] son
conmutativos, asociativos, distributivos, etc..., tienen las mismas propiedades algebraicas que
los valores de [0, 1]. En definitiva, una cadena --borrosa normal puede tratarse de la misma
manera que una cadena borrosa normal, aunque para diferenciarlas a efectos simbólicos, se
exprese por [ N ].
En particular, supongamos que la matriz de la Figura 5 describe el comportamiento estimado
como posible del balance de caja. Los números de la primera columna vertical (filas) son la
cantidad de dinero (u.m.) en la contabilidad de caja en la mañana del día n. Los números de la
fila superior (columnas) son el balance de caja en unidades monetarias en la mañana del día
n+1. La tabla señala que, por ejemplo, si el balance de caja es 2 en el día n, la posibilidad de que
sea 1 el día n+1 es de [0.2, 0.4] (el número marcado en la fila 2, columna 1, es de [0.2, 0.4]).
1
2
3
4
5
1
[.2, .4]
1
[.3, .5]
0
0
2
[.2, .4]
1
[.3, .5]
0
0
3
0
[.4, .7]
.35
1
0
4
0
0
.6
1
[.1, .4]
5
[.2, .4]
1
[.3, .5]
0
0
Figura 5. Relación --borrosa normal del balance de caja.
De esta forma, la Figura 5 muestra la matriz incierta de transición donde se supone a efectos
del sistema de control de gestión de la liquidez, una cota superior de 5 y una cota inferior de 1,
con el punto de retorno igual a 2. En dicha matriz, las filas 2, 3 y 4 muestran las valuaciones
(opinión subjetiva) de que el sistema se mueva de un estado a otro y las filas 1 y 5 se deducen de
forma semejante que en el caso descrito en el epígrafe anterior.
Esta relación --borrosa normal facilita al controller contestar a la pregunta sobre el nivel de
presunción de que el sistema se encuentre en un estado específico en un momento futuro
cercano, pues, al utilizar valuaciones, resultará interesante conocer, a partir de estos datos
subjetivos, los resultados para los que la presunción es más elevada. Ahora bien, como hemos
señalado, el encadenamiento con datos borrosos, de acuerdo con los profesores citados, se
efectuará mediante la composición maxmin, tomando las valuaciones mínimas y después el
máximo de los mínimos. En nuestra aplicación, por ejemplo, si nos interesase conocer cuál es la
posibilidad de que después de dos "pasos" nos encontremos en el estado 3, si el estado inicial
2
fuera de 2, operaríamos como sigue a continuación :
(2) A efectos de comparación entre dos intervalos de confianza, conviene recordar que éstos no forman como R un orden
total, sino un orden parcial. Para pasar de un orden parcial a un orden total es necesario establecer de manera arbitraria un
criterio, y, si con uno no basta, recurriremos a otro. Así, por ejemplo, podemos tomar como primer criterio la suma de las
abscisas de los extremos o bien la abscisa de la posición media:
([a1, a2]) = a1 + a2 / 2
Se escribirá entonces:
A>B
si
a1 + a2 / 2 > b1 + b2 / 2
Estado inicial
&1
Después de un paso
Después de dos pasos
1&
&
2&
&
&2
3&
&
&3
4&
&
&4
5&
&
&5
(a2, a3) = ([.2,.4] Y [.3,.5] ) Z (1 Y [.3,.5]) Z ([.3,.5] Y 0.35]) Z (0 Y 0.6) Z
(0 Y [.3,.5]) = [.3, .5]
Z
n
Asimismo, de forma similar a lo considerado en la expresión (10), se calculará [ N ] hasta
n+1
n
que [ N ] = [ N ] , donde se tiene
n
*
lim [ N ] = [ N ]
n
No obstante, con la composición maxmin es conveniente adoptar como relación --borrosa
normal límite el cierre transitivo [ N ], es decir:
2
3
[ N ] = [ N ] F [ N ] F [ N ] .....
(26)
y si a1 + a2 = b1 + b2, es preciso adoptar otro criterio, como por ejemplo:
A>B
si
a2 > b2
y a1 + a2 = b1
+ b2
o bien:
A>B
si
a1 > b1
y a1 + a2 = b1 + b2
Por otro lado, si se tiene que a1 b1 y a2 b2, A y B son entonces comparables y tenemos A B.
n+1
n
ya que, exceptuando el caso en que [ N ] es reflexiva no siempre se cumple que [ N ] H [ N ]
y el camino más "fuerte" en el grafo valuado se obtiene considerando el cierre transitivo.
En nuestro caso de aplicación tenemos:
[N]
*
[N]
=
.2,.4
1
.3,.5
0
0
.2,.4
1
.3,.5
0
0
.2,.4
1
.3,.5
0
0
.2,.4
1
.3,.5
0
0
0
.4,.7
.35
1
0
0
.4,.7
.35
1
0
0
0
.6
1
.1,.4
0
0
.6
1
.1,.4
.2,.4
1
.3,.5
0
0
.2,.4
1
.3,.5
0
0
*
2
[N]
=
3
[N]
[.2, .4]
1
[.3, .5]
[.3, .5]
0
[.2, .4]
1
[.3, .5]
[.3, .5]
0
[.2, .4]
[.4, .7]
.6
1
[.1, .4]
[.1, .4]
[.4, .7]
.6
1
[.1, .4]
[.2, .4]
1
[.3, .5]
[.3, .5]
0
=
[.2, .4]
1
[.3, .5]
[.3, .5]
[.1, .4]
[.2, .4]
1
[.3, .5]
[.3, .5]
[.1, .4]
[.2, .4]
[.4, .7]
.6
1
[.1, .4]
[.2, .4]
[.4, .7]
.6
1
[.1, .4]
[.2, .4]
1
[.3, .5]
[.3, .5]
[.1, .4]
=
4
[N]
=
[.2, .4]
1
[.3, .5]
[.3, .5]
[.1, .4]
[.2, .4]
1
[.3, .5]
[.3, .5]
[.1, .4]
[.2, .4]
[.4, .7]
.6
1
[.1, .4]
[.2, .4]
[.4, .7]
.6
1
[.1, .4]
[.2, .4]
1
[.3, .5]
[.3, .5]
[.1, .4]
4
3
Nos detenemos: [ N ] = [ N ] y se obtiene
[N]
=
[.2, .4]
1
[.3, .5]
[.3, .5]
[.1, .4]
[.2, .4]
1
[.3, .5]
[.3, .5]
[.1, .4]
[.2, .4]
[.4, .7]
.6
1
[.1, .4]
[.2, .4]
[.4, .7]
.6
1
[.1, .4]
[.2, .4]
1
[.3, .5]
[.3, .5]
[.1, .4]
En nuestro caso de aplicación, supóngase que el controller llega el lunes por la mañana y
comprueba que el sistema está en el estado 3 y desea saber cual es la posibilidad de encontrar el
sistema en el estado 1 el miércoles por la mañana, ya que entonces deberá vender valores para
obtener dinero y a él le convendrá planificar cuáles valores de su cartera deberá vender.
De esta forma, tenemos:
=
1
2
3
4
5
0
0
1
0
0
*
[N]
=
1
2
3
4
5
[.2, .4]
[.4, .7]
.6
1
[.1, .4]
Por tanto, si el estado inicial del sistema se encuentra en 3 en un momento futuro cercano el
máximo de presunción se encontrará en 4. No obstante, centrándonos en la cuestión planteada
arriba, podemos observar que se supone una posibilidad de [0.2, 0.4] que el sistema esté en el
estado 1 el miércoles.
Conviene señalar que, al utilizar la concepción del máximo de presunción, carece de sentido
la noción de estado persistente. En otras palabras, no podemos decir que el número de veces en
las que el sistema estará en el estado 1 durante el año sea de 260 x [0.2, 0.4] = [52, 104].
Sin embargo, sí es posible, en lugar de pretender llegar al caso límite, plantear la situación en
el futuro después de algunas etapas relativamente cortas. Si las matrices correspondientes tienen
un número reducido de estados, estos cálculos pueden tener una significación real mientras que
en el caso contrario se necesitará la intervención de una bola de cristal.
IV. Referencias Bibliográficas
BACHILLER CACHO, A. et al.: "Gestión económico-financiera del circulante". Pirámide.
Madrid, 1982.
BAUMOL, W.J.: "The Transactions Demand for Cash: An Inventory Theoretic Approach".
The Quarterly Journal of Economics. Vol. 66, N 4. November 1952, pp. 545-
556.
BERANEK, W.: "Análisis para la toma de decisiones financieras". Labor. Barcelona, 1975.
CAÑIBANO CALVO, L. y BUENO CAMPOS, E.: "Autofinanciación y tesoreria en la
empresa: el cash-flow". Pirámide. Madrid, 1983.
CHANAS, S. and KOLODZIEJYK, W.: "Maximun flow in a network with fuzzy arc
capacities". Fuzzy Sets & Systems. Vol. 8, N 2, August 1982, pp. 165-174.
CZOGALA, E. and ZIMMERMANN, H.J.: "The aggregation opperations for decisionmaking in probabilistic fuzzy environment". Fuzzy Sets & Systems. Vol. 13,
N
3, August 1984, pp. 223-240.
DELGADO, M. et al.: "Some structural and optimization problems on fuzzy graphs". In
KULIKOWSKI, R. and RUDNICKI, J. (eds.): "System Analysis and Computer
Science". Omnitech Press. Poland, 1990, pp. 47-63.
FEDRIZZI, M. et. al. (eds.): "Interactive Fuzzy Optimization". Springer-Verlag. Berlin,
1991.
GIL ALUJA, J.: "El estudio dinámico de la elección de inversiones". Técnica Contable,
Febrero 1967, págs. 41-50 y 66.
GIL LAFUENTE, A.M.: "El análisis financiero en la incertidumbre". Ariel. Barcelona,
1990.
GREGORY, G.: "Cash flow Models: A Review". OMEGA. Vol. 4, N 6, 1976, pp. 643656.
ITAKURA, H. and NISHIKAWA, Y.: "Fuzzy network technique for technological
forecasting". Fuzzy Sets & Systems. Vol 14, N 2, November 1984, pp. 99114.
KAUFMANN, A.: "Métodos y Modelos de la programación matemática". CECSA. México,
1966.
KAUFMANN, A. y GIL ALUJA, J.: "Introducción de la teoría de los subconjuntos borrosos
a la gestión de las empresas". Milladoiro. Santiago de Compostela, 1986.
KAUFMANN, A. y GIL ALUJA, J.: "Técnicas operativas de gestión para el tratamiento de
la incertidumbre". Hispano Europea. Barcelona, 1987.
KAUFMANN, A. y GIL ALUJA, J.: "Modelos para la investigación de efectos olvidados".
Milladoiro. Santiago de Compostela, 1988.
KAUFMANN, A. y GIL ALUJA, J.: "Las matemáticas del azar y de la incertidumbre".
Centro de Estudios Ramón Areces. Madrid, 1990.
KAUFMANN, A. y GIL ALUJA, J.: "Nuevas técnicas para la dirección estratégica".
Universidad de Barcelona. Barcelona, 1991.
MILLER, H. and ORR, A.: "A Model of the Demand for Money by Firms". The Quarterly
Journal of Economics. Vol. 80, N 3. August 1966, pp. 413-435.
PATINKIN, D.: "Money, Interest and Prices". Row, Peterson & Co. Evanston, 1956.
ZIMMERMANN, H.J.: "Using fuzzy sets in operations research". European Journal of
Operations Research, Vol. 13, N 3. 1983, pp. 201-216.