infinitésimos o infinitos equivalentes.
Anuncio

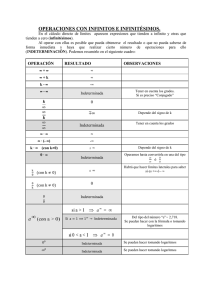
INFINITÉSIMOS O INFINITOS EQUIVALENTES.
Para el estudio de límites de sucesiones (y por tanto también de series), se suelen utilizar los
INFINITÉSIMOS o INFINITOS EQUIVALENTES, que son sucesiones tales que su diferencia
tiende a 0, cuando n tiende a infinito.
Si (xn) y (bn) son dos sucesiones reales, tales que:
bn = n–r. (K+εn);
para un r ∈ N, una constante K ∈ R y un ε n > 0.
Y se cumple, que:
Lim n à∞ (xn – bn ) = 0.
Entonces, se denomina:
FORMA NORMAL de ( x n )
= F. N. ( x n ) = ( b n ).
PARTE PRINCIPAL de ( x n )
= P. P. (x n )
= n – r . K.
# Ejemplo:
Si b n = ( 1 + (1/n²) )½ - 1 ≈ Ln [ ( 1 + (1/n²) )½ ]≈ (1/ 2.n²).
La forma normal de b n = (1/n²).( (1/2) + ε ).
La parte principal de b n = ( 1 / 2.n² )
Si c n = n . ( 1 + (2/n) + (1/n²) ) ½ - (1/2) ≈ n . ( 1 - (1/2) ≈ (n/2).
La forma normal de c n = n.( (1/2) + ε ).
La parte principal de c n = (n/2).
C INFINITESIMOS O INFINITOS EQUIVALENTES:
x
x
x
x
x
n
→ 0 ⇒ sin x n ≈ x n ≈ tan ( x n )
n
→ 0 ⇒ acos x n ≈ x n ≈ artan ( x n )
n
→ 0 ⇒ 1 - cos x n ≈ x²n / 2
n
→ 0 ⇒ Ln ( 1 + x n ) ≈ x n
n
→ 1 ⇒ Ln (x n ) ≈ x n - 1
n → ∞ ⇒ n! ≈ ( 2. π e (-n) . n n ) ½
n→∞ ⇒
k
∑ ai . n k−i
i=1
≈ a0 . n k .
k
n → ∞ ⇒ ln ∑ ai . n k−i ≈ Ln [ n k ].
i=1
a → a; a ∈ R – {0}; ⇒ a n ≈ a.
n