Utilización de calculadoras TI 1 Asignación 3: Resolución de
Anuncio
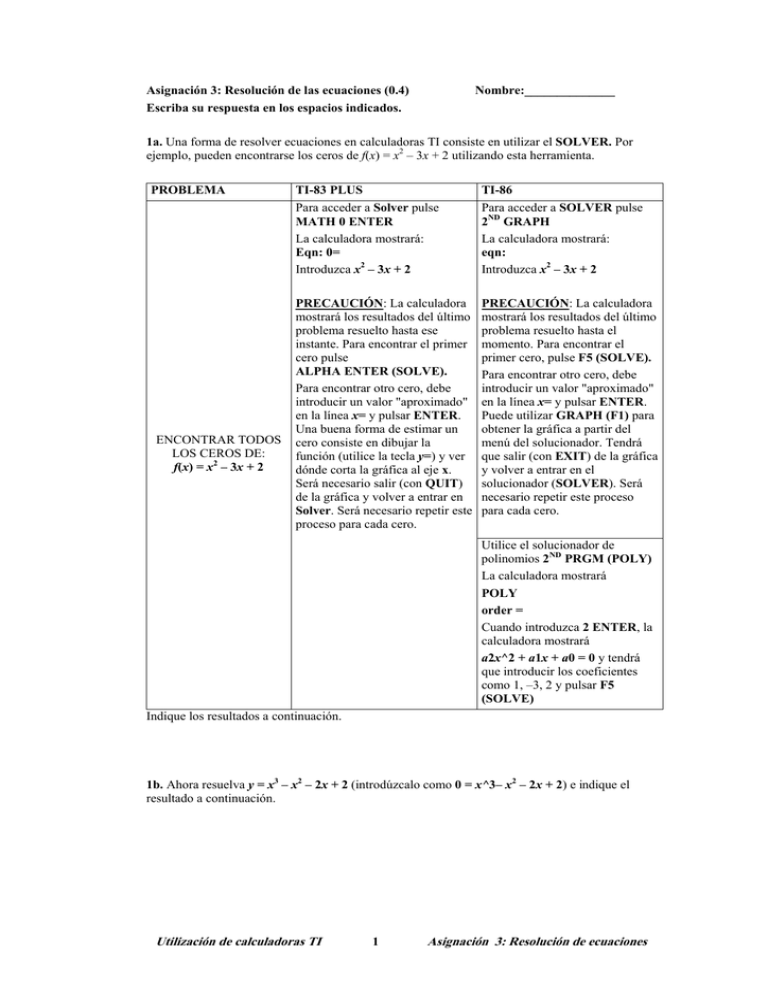
Asignación 3: Resolución de las ecuaciones (0.4) Escriba su respuesta en los espacios indicados. Nombre:______________ 1a. Una forma de resolver ecuaciones en calculadoras TI consiste en utilizar el SOLVER. Por ejemplo, pueden encontrarse los ceros de f(x) = x2 – 3x + 2 utilizando esta herramienta. PROBLEMA ENCONTRAR TODOS LOS CEROS DE: f(x) = x2 – 3x + 2 TI-83 PLUS Para acceder a Solver pulse MATH 0 ENTER La calculadora mostrará: Eqn: 0= Introduzca x2 – 3x + 2 TI-86 Para acceder a SOLVER pulse 2ND GRAPH La calculadora mostrará: eqn: Introduzca x2 – 3x + 2 PRECAUCIÓN: La calculadora mostrará los resultados del último problema resuelto hasta ese instante. Para encontrar el primer cero pulse ALPHA ENTER (SOLVE). Para encontrar otro cero, debe introducir un valor "aproximado" en la línea x= y pulsar ENTER. Una buena forma de estimar un cero consiste en dibujar la función (utilice la tecla y=) y ver dónde corta la gráfica al eje x. Será necesario salir (con QUIT) de la gráfica y volver a entrar en Solver. Será necesario repetir este proceso para cada cero. PRECAUCIÓN: La calculadora mostrará los resultados del último problema resuelto hasta el momento. Para encontrar el primer cero, pulse F5 (SOLVE). Para encontrar otro cero, debe introducir un valor "aproximado" en la línea x= y pulsar ENTER. Puede utilizar GRAPH (F1) para obtener la gráfica a partir del menú del solucionador. Tendrá que salir (con EXIT) de la gráfica y volver a entrar en el solucionador (SOLVER). Será necesario repetir este proceso para cada cero. Utilice el solucionador de polinomios 2ND PRGM (POLY) La calculadora mostrará POLY order = Cuando introduzca 2 ENTER, la calculadora mostrará a2x^2 + a1x + a0 = 0 y tendrá que introducir los coeficientes como 1, –3, 2 y pulsar F5 (SOLVE) Indique los resultados a continuación. 1b. Ahora resuelva y = x3 – x2 – 2x + 2 (introdúzcalo como 0 = x^3– x2 – 2x + 2) e indique el resultado a continuación. Utilización de calculadoras TI 1 Asignación 3: Resolución de ecuaciones 2a. Utilice SOLVER para resolver la ecuación cos x = x2 – 1 e indique el resultado a continuación. Puede examinar la gráfica para determinar el número de ceros que la función tiene. Introduzca su ecuación como sigue: PROBLEMA Resuelva cos x = x2 – 1 TI-83 PLUS Introduzca su ecuación como Ø = cos(x) – x2 + 1 y la gráfica como y = cos(x) – x2 + 1 TI-86 Introduzca su ecuación como cos x = x2 – 1y utilice la opción de gráfica como antes para estimar el segundo cero Indique el resultado a continuación. 2b. Podemos hallar todos los ceros de cos x = x2 – 1 comenzando a partir de la gráfica. PROBLEMA Resuelva cos x = x2 – 1 a partir de la gráfica TI-83 PLUS Halle la gráfica de y = cos(x) – x2 + 1. Vaya a CALC (2ND TRACE) y seleccione 2 zero. Utilice las flechas de cursor para mover el cursor a la izquierda del cero con el fin de definir el límite izquierdo (Left Bound) y luego para determinar el límite derecho (Right Bound). Pulse ENTER para fijar cada límite. A continuación pulse ENTER para realizar la estimación (Guess) y la calculadora indicará cuál es el cero. TI-86 Dibuje la gráfica de y = cos x – x2 +1 En el menú GRAPH seleccione MORE MATH ROOT (F1). Utilice las teclas de cursor para mover el cursor a la izquierda del cero con el fin de definir el límite izquierdo (Left Bound) y luego para fijar el límite derecho (Right Bound). Pulse ENTER para fijar cada uno de los límites. A continuación, pulse ENTER para que se realice la estimación (Guess) y la calculadora indicará cuál es el cero. Dibuje la gráfica e indique el resultado a continuación. ¿Concuerdan estos resultados con los del apartado 2a? –10 ⱕ x ⱕ 10, –10 ⱕ y ⱕ 10 2c. Ahora cambie las partes a y b para resolver la ecuación cos x = x2 – 5. Acuérdese de sustituir la x = con el valor apropiado sugerido por su gráfica. Indique su solución a continuación. –10 ⱕ x ⱕ 10, –10 ⱕ y ⱕ 10 Utilización de calculadoras TI 2 Asignación 3: Resolución de ecuaciones