1.4 Clase Variables Aleatorias

Humberto Villalobos
7-03-05
Variables Aleatorias
PROBABILIDAD
Y
• Probabilidades Î Espacio Muestral
ESTADÍSTICA
HUMBERTO VILLALOBOS TORRES
UNIVERSIDAD TÉCNICA FEDERICO SANTA MARÍA
DEPARTAMENTO
DE
MATEMÁTICAS
22/09/2007
22/09/2007
Variables Aleatorias
Variables Aleatorias
• Una variable aleatoria, es una función que
permite trabajar cualquier espacio muestral
de manera cuantitativa.
• Esquemáticamente corresponde:
DEFINICIÓN 1: Se dice que X es una variable
aleatoria (v.a.) si es una función que toma los
elementos de Ω y los transforma en puntos
sobre la recta de los reales.
22/09/2007
22/09/2007
Variables Aleatorias
Cada elemento del espacio muestral
tiene asociado un punto en la recta
Variables Aleatorias
DEFINICIÓN 2: Se dice que X es una v.a. si es
una función que toma valores en probabilidad,
es decir, no se puede predecir con certeza sus
resultados.
¿qué se puede predecir con certeza?
• Todos los elementos asociados a un espacio
muestral elemental están asociados a uno de los
posibles valores del recorrido de la variable.
• El espacio muestral original “induce” un espacio
muestra Rx asociado a la Variable Aleatoria X.
• Luego par cualquier subconjunto de Ω, se induce
un subconjunto en Rx.
22/09/2007
Primera Clase
• Cantidad de calorías consumidas.
• Rentabilidad de un instrumento de
renta variable.
• Nacimiento y Muerte.
22/09/2007
1
Humberto Villalobos
7-03-05
Tipos de Variables Aleatorias
Tipos de Variables Aleatorias
• Una variable aleatoria es siempre
cuantitativa y se puede clasificar en
los siguientes grupos:
22/09/2007
• Variable discreta finita.
22/09/2007
Tipos de Variables Aleatorias
Tipos de Variables Aleatorias
• Variable discreta infinita.
• Variable continua no acotada.
22/09/2007
22/09/2007
Función de Distribución
Función de Distribución
• Se tiene que X es una variable aleatoria
(v. a.) discreta, donde los valores que toma
son:
• Sobre la base de esta v. a. discreta, cuyo
concepto se puede también extender a
variables continuas, puede construir la
función de probabilidad acumulada, como la
probabilidad de que la variable aleatoria X
sea menor o igual a x ∈ e.
x1, x2, x3, ... , xk, con
x1 < x2 < x3 < ... < xk, entonces:
DEFINICIÓN 3: Sea X es una v.a., entonces, se
define la función de distribución de probabilidad,
como la probabilidad de que la variable
aleatoria X tome algún valor menor o igual que
x ∈ e, y se simboliza por: FX(x) = [X ≤ x].
Se tiene que en e, se representan por:
22/09/2007
Primera Clase
22/09/2007
2
Humberto Villalobos
7-03-05
Función de Distribución
Función de Distribución
• La función de distribución cumple con
las siguientes propiedades:
• En el caso que una variables sea cuantitativa
existe un continuo de valores que puede
tomar x, razón por la cual la función de
distribución está dada por:
x
FX ( x) = P[X ≤ x] =
∫
f T (t )dt
−∞
22/09/2007
22/09/2007
Función de Distribución
Función de Distribución
• APLICACIÓN 1: Se descubrió que cuando se
presenta un daño en un sistema eléctrico,
existe la probabilidad de que un conjunto de
partes específicas causen el daño. Si el tiempo
de demora en revisar las partes (las cuales se
hacen individualmente) y el costo por
reemplazo se indica a continuación:
• APLICACIÓN 1: Se descubrió que cuando …
Determine la función de distribución del
tiempo de demora en la revisión de las
partes.
Función de Distribución
F(x )
1,2
0,8
0,4
0,0
2,35
3,35
4,35
5,35
6,35
Tiempo (hrs)
22/09/2007
22/09/2007
Función de Distribución
Función de Distribución
• APLICACIÓN 2: Un jugador lanza dos
• APLICACIÓN 2: Un jugador … Determine la
monedas. Gana $10 ó $20 según aparezca una ó
dos caras respectivamente. Por otro lado pierde
$50 si aparecen dos sellos. Determine la función
de distribución de la ganancia en el juego.
22/09/2007
Primera Clase
función de distribución de la ganancia en el
juego.
22/09/2007
3
Humberto Villalobos
7-03-05
Función de Distribución
Función de Cuantía o Masa
DEFINICIÓN 4: Sea X una v.a discreta,
entonces se define la función de cuantía ó masa
de probabilidad, como la probabilidad de que
la variable aleatoria X tome un valor específico
x, y se simboliza por fx(x) = [X = x], y cumple
con las siguientes propiedades:
• APLICACIÓN 2: Un jugador … Determine la
función de distribución de la ganancia en el
juego.
g < -50
0
1
 4 g < 10
FG ( g ) 
3
 4 g < 20
1
g ≥ 20

22/09/2007
22/09/2007
Función de Cuantía o Masa
Función de Cuantía o Masa
• APLICACIÓN 1: Se descubrió que cuando se
presenta … Determine la función de cuantía
de probabilidad asociada al costo por
reemplazo de las partes del sistema
22/09/2007
• APLICACIÓN 1: ¿Cuál es la probabilidad de
falla del sistema por causa de sólo dos de sus
partes?.
22/09/2007
Función de Cuantía o Masa
Función de Cuantía o Masa
• APLICACIÓN 1: Si el sistema eléctrico se
encuentra en una red que tiene: 3 partes de
A; 15 de B; 3 de C y 4 de D. ¿Cuál es la
probabilidad que al escoger cinco partes de
la red al azar no menos de 2 sean de B?.
• APLICACIÓN 3: La demanda semanal de ciertos
artículos se supone una variable aleatoria cuya
distribución de probabilidad se entrega en la
siguiente tabla:
Determine la constante c
22/09/2007
Primera Clase
22/09/2007
4
Humberto Villalobos
7-03-05
Función de Cuantía o Masa
Función de Densidad o Masa
• APLICACIÓN 3: La demanda semanal …
Realice un bosquejo de la función de cuantía y
distribución de la demanda del artículo
FUNCIÓN DE DISTRIBUCIÓN
0,35
0,30
1,0
P rob ab ilid ad
P ro b ab ilid ad
FUNCIÓN DE CUANTÍA
DEFINICIÓN 5: Sea X es una v.a. continua,
entonces fx(x) es una función de densidad de
probabilidad (f.d.p.) para X, sí ‘fx(x)’,
satisface las propiedades:
0,25
0,20
0,15
0,10
0,05
0,00
0
1
2
3
4
5
0,8
0,6
0,4
0,2
0,0
-1
Número de artículos demandados
0
1
2
3
4
5
6
Número de artículos demandados
22/09/2007
22/09/2007
Función de Distribución
Función de Densidad o Masa
• En el caso que una variable sea
absolutamente continua, existe un continuo
de valores que puede tomar x, razón por la
cual la función de distribución está dada por:
• APLICACIÓN 4: Cierto vendedor de un
producto petrolero vende una cantidad
aleatoria, X, en cientos galones por día
[CG/d],. Supóngase que X, tiene una función
de densidad de probabilidad dada por:
x
FX ( x) = P[X ≤ x] =
∫
f T (t )dt
κ x (2 − x) 2
f x ( x) = 
0
−∞
22/09/2007
0 ≤ x ≤ 2
e.o.c.
22/09/2007
Función de Densidad o Masa
Función de Densidad o Masa
• APLICACIÓN 4: Cierto vendedor … Determine la
• APLICACIÓN 4: Cierto vendedor de un …
Determine la función de distribuciones de la
variable venta del producto.
constante κ de la variable venta del producto.
2
∫
0
2
 2
 4x 4x3 x4 
2
−
+
κ x (2- x) ∂x = κ 
=1
3
4 
 2
0
0


2
f X ( x) ∂x = 1
∫
• ¿Cuál es la probabilidad que
la venta del producto sea
mayor a 1 y menor a 5/4?.
22/09/2007
Primera Clase
22/09/2007
5
Humberto Villalobos
7-03-05
Función de Densidad o Masa
Función de Densidad o Masa
• APLICACIÓN 5: La cantidad de cierto
producto, en cientos de kilogramos, vendida
diariamente en un supermercado, es una
variable aleatoria con la siguiente función de
densidad :
• APLICACIÓN 4: La cantidad de cierto
producto, en … Determine la constante m de la
variable venta del producto.
1
m
∫
 1
 2 , 0 ≤ x <1

f ( x ) = 2 − x , 1 ≤ x < m
 0 , en otro caso

f X (x) dx = 1
0
0
m
1
m
 1 
2
 1x +  2 x − x   = 1
2
2  
 0 
1 

− 1 + 2m −
22/09/2007
1
∫ 2 dx + ∫ (2 − x)dx =1
22/09/2007
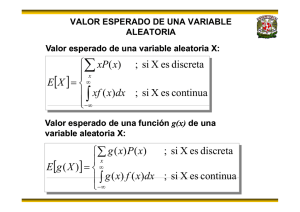
Valores Esperados
m2
= 1
2
Valores Esperados
DEFINICIÓN 6: Sea X una v.a., entonces, se
define el valor esperado de una función real,
g(X) de X, como:
DEFINICIÓN 7: Sea X es una v.a., se define el
valor esperado ó esperanza matemática de X,
como:
PROPIEDADES: Sean a y b constantes y X una
variable aleatoria, entonces:
22/09/2007
22/09/2007
Valores Esperados
Valores Esperados
DEFINICIÓN 8: La varianza de una variable
aleatoria X, se define como el valor esperado del
cuadrado de la diferencia entre la variable aleatoria
y su valor esperado, que está dada por:
• APLICACIÓN 3: La demanda semanal de …
Determine el valor esperado de demanda de
artículos y su desviación estándar :
PROPIEDADES: Sean a y b constantes y X una
variable aleatoria, entonces:
22/09/2007
Primera Clase
22/09/2007
6
Humberto Villalobos
7-03-05
Propiedades de Valores Esperados
Valores Esperados
• APLICACIÓN 3: La demanda semanal de … Si la
• APLICACIÓN 4: Cierto vendedor de un
producto petrolero … Determine la esperanza
y varianza de la venta del producto.
utilidad ‘U’, en millones, puede expresar en
función de la demanda a través de:
U = 20 × C – 50
¿Cuál es la Utilidad esperada mensual y su
varianza?
22/09/2007
22/09/2007
Valores Esperados
Propiedades de Valores Esperados
APLICACIÓN 4: Cierto vendedor de un
producto petrolero … ¿Cuál es la probabilidad
que la venta del producto sea mayor a su valor
esperado y menor a 14 veces su varianza?.
APLICACIÓN 4: Cierto vendedor de un producto
22/09/2007
petrolero … Si los costos diarios asociados a la
empresa están en función de la venta según la
siguiente ecuación C(X) = 10 + 5X. Determine los
costos diarios esperados, su desviación estándar.
22/09/2007
Transformaciones de Variables
Transformaciones de Variables
• Las transformaciones en variables aleatorias son
de uso común, en algunos casos, su interés es sólo
para determinar un valor esperado, y en otros
para determinar la nueva ley de probabilidad
que rige a la variable transformada,
esquemáticamente se desea:
• Las transformaciones se pueden dar, desde una
variable:
–Discreta
–Continua
–Continua
–Continua
⇒
⇒
⇒
⇒
Discreta
Discreta
Continua
Mixta
• Las transformaciones de variables discretas son
de sencilla solución.
• Las transformaciones de variables continuas a
través de otra función continua, bajo ciertas
restricciones permiten obtener nuevas funciones
de masa de probabilidad.
22/09/2007
Primera Clase
22/09/2007
7
Humberto Villalobos
7-03-05
Transformaciones de Variables
Transformaciones de Variables
APLICACIÓN 5: Una planta industrial … En el
costo de producción debe considerarse el valor
esperado de las pérdidas por detención del
proceso debido a fallas. Determine la función de
masa para el costo de producción.
APLICACIÓN 5: Una planta industrial funciona
en forma continua de lunes a viernes, produciendo
12.000 unidades en ese período. Si el proceso se
detiene una vez durante la semana por fallas
técnicas, se produce una pérdida de $ 6000; si se
detiene dos veces, la pérdida es de $ 12300; si se
detiene tres veces la pérdida es de $ 18100; si se
detiene cuatro veces o más, la pérdida que se produce
es de $ 25000. El número de fallas que se produce en
una semana sigue un modelo probabilístico con la
siguiente función de cuantía:
Rec C : {0, 6000, 12300, 18100, 25000}
0
22/09/2007
22/09/2007
Transformaciones de Variables
Transformaciones de Variables
APLICACIÓN 5: Una planta industrial … En el
APLICACIÓN 5: Una planta industrial … En el
costo de producción ... Determine la varianza y el
costo esperado de producción por unidad.
costo de producción ... Determine la función de
distribución para el costo de producción.
22/09/2007
22/09/2007
Transformaciones de Variables
Transformaciones de Variables
APLICACIÓN 6: La demanda semanal de
APLICACIÓN 6: La demanda semanal …
cierta bebida de fantasía, en miles de litros, de un
determinado local de Mall muy concurrido, es
una variable aleatoria continua, definida por X,
que tiene por función de densidad de
probabilidad a:
 κ ( x - 1)
f X ( x) = 

0
Suponga que los costos asociados a la producción
de esta bebida, en millones, están dados por:
10

C (X) = 40
100

1< x < 2
e.o.c.
¿Cuál es la función de distribución asociada al
costo de producción?
¿Cuál debe ser el valor de ,?
1
∫f
0
22/09/2007
Primera Clase
X ( x) dx
=1
2
 2
x

κ  − x  =1
 2

1


x < 1,2
1,2 ≤ x < 1,5
x ≥ 1,5
Rec C(X) : {10, 40, 100}
⇒ κ=2
22/09/2007
FINITO
8
Humberto Villalobos
7-03-05
Transformaciones de Variables
Transformaciones de Variables
APLICACIÓN 6: La demanda semanal … la
APLICACIÓN 6: La demanda semanal … la
función de distribución asociada al costo de
producción :
función de masa de probabilidad asociada al
costo de producción sería:
Entonces, el costo de producción esperado:
22/09/2007
22/09/2007
Transformaciones de Variables
Transformaciones de Variables
• En el caso de variables aleatorias continuas,
cuya función de masa de probabilidad es
f(x).
• Considere la función Y = g(X) que cumpla
los requisitos.
APLICACIÓN 7: Sea X una variable aleatoria
continua con función de densidad f(x). Considere
a Y = g(X), una función de X. Entonces,
– Es una función 1-1 en el Soporte de X.
– Su función inversa existe y es diferenciable en
X – A, donde A es un conjunto con
probabilidad cero.
• Entonces es posible determinar la función
de densidad de la variable aleatoria Y a
partir de X.
22/09/2007
22/09/2007
Transformaciones de Variables
Transformaciones de Variables
APLICACIÓN 7: Sea X una variable aleatoria
APLICACIÓN 6: La demanda … El costo (en
miles de $) de cada interrupción está dado por
C(T$) = 10 + 20T. Encuentre el costo esperado y
su variabilidad. Determine la función de
densidad del costo (fC(c)) :
continua con función de densidad f(x). Considere
a Y = g(X), una función de X. Entonces,
Esta aplicación representa el teorema de
transformación integral, para transformaciones
donde el los requisitos pre-establecidos sean
satisfechos.
22/09/2007
Primera Clase
22/09/2007
9
Humberto Villalobos
7-03-05
Transformaciones de Variables
APLICACIÓN 6: La demanda … ¿Cuál es la
probabilidad que el costo sea superior a $25 e
inferior a $40?
22/09/2007
Primera Clase
10