polinomios -2 - Almagro

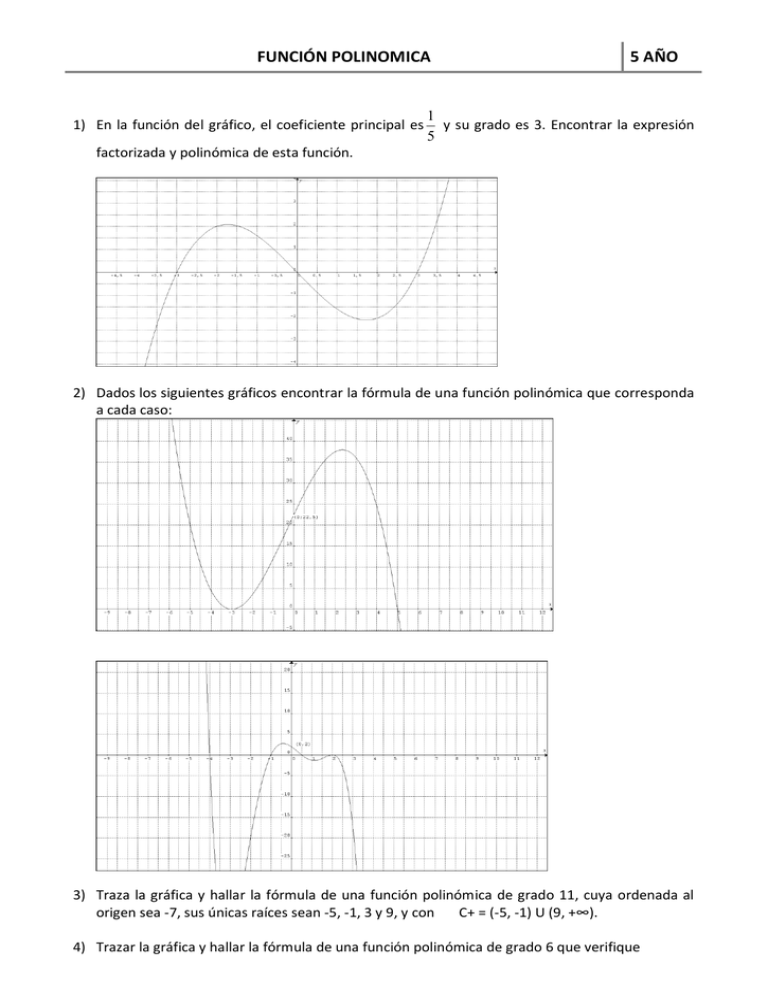
FUNCIÓN POLINOMICA
1) En la función del gráfico, el coeficiente principal es
5 AÑO
1
y su grado es 3. Encontrar la expresión
5
factorizada y polinómica de esta función.
2) Dados los siguientes gráficos encontrar la fórmula de una función polinómica que corresponda
a cada caso:
3) Traza la gráfica y hallar la fórmula de una función polinómica de grado 11, cuya ordenada al
origen sea -7, sus únicas raíces sean -5, -1, 3 y 9, y con
C+ = (-5, -1) U (9, +∞).
4) Trazar la gráfica y hallar la fórmula de una función polinómica de grado 6 que verifique
FUNCIÓN POLINOMICA
5 AÑO
f(-1) = -1.5 y con C+ = (-∞, -3) U (1, 4) U (4, +∞).
5) Los siguientes gráficos representan, aproximadamente, a las funciones polinómicas:
P(x) = x 3 + 2x 2 - 2x + 3; Q(x) = x 3 - 2x 2 - 7x - 4 y F(x) = x 3 + x 2 - 4 x – 4
a) Factorizar todas las funciones.
b) A partir de los datos incluidos en los gráficos, identificar qué gráfico que corresponde a cada
función. Justificar.
6) R(x) es un polinomio de grado 5 que tiene una raíz doble en x = 3 ; R(0) = 18, su coeficiente
principal es -1. Además es divisible por (x-1) y R(2)= -12. Hallar la forma factorizada y
polinómica de R(x) . Obtener un gráfico aproximado de la función.
7) Hallar la función polinómica de grado 3 que corta el eje x en (-1,0) , (-5,0) y (1,0) y en la cual
P(0)=2. Determinar sus intervalos de positividad y negatividad. Obtener un gráfico aproximado.
8) S(x) es una función polinómica de grado 3 cuyo gráfico corta el eje de las abscisas en -4, 2 y 3 y
pasa por el punto (1, 4). Halla S(x) y determinar sus intervalos de positividad y negatividad.
Obtener un gráfico aproximado.
9) Determinar la función polinómica de grado 4 cuyo conjunto de negatividad es C- = (-3,0); su
1
coeficiente principal es
, P(2)= 1. Obtener un gráfico aproximado.
90
10) La siguiente gráfica corresponde a una función polinómica de grado 4. Hallar la fórmula de
dicha función. Indicar sus intervalos de positividad y negatividad.
FUNCIÓN POLINOMICA
5 AÑO
11) La siguiente gráfica corresponde a una función polinómica de grado 5. Con los datos del grafico
escribir su expresión factorizada sabiendo que su coeficiente principal es -0,2.
12) Encontrar un polinomio R(x) de grado 6, cuyas raíces son C 0=
especialización en R(-1) =
13) Hallar
la
función
y su
2, 0, 2 , C
9
. Realizar un gráfico aproximado.
5
polinómica
P(x)
de
menor
grado,
con
C
,
7
5
7
,
4
,
7
7
49
, 1
1,1
1, y P (0)
y trazar un gráfico aproximado.
5
4
20
14) Determinar la función polinómica de grado 3 cuyo conjunto de positividad es C (1, ) , su
coeficiente principal es 1, P(0)= -4 y una de sus raíces es doble. Obtener un gráfico
aproximado.
C
15) Factorizar , realizar un gráfico aproximado y analizar cada una de las siguientes funciones
a) P( x) x 4 x
b) Q(x) = 5x 3 10 x 2
5x 10
c) T(x) = 2x 2 162
d) V(x) = x 4 12 x 2 36
e) W(x) = 2 x 7 3x 6 5 x 5
f) Y(x) = x 4 4 x 3 x 2 16 x 12
g) S(x)= x 3
x2
x 1
FUNCIÓN POLINOMICA
h) U(x)= x 4 1 9 x 9 x 3
i) O(x)= 4 x 5 x 3
4x 2
5 AÑO