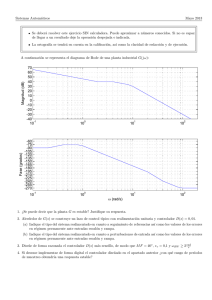
Introducción a la Teor´ıa de Invariantes Geométricos

Introducción a la Teorı́a de Invariantes Geométricos
12 de diciembre de 2010
Claudia Reynoso
[email protected]
Departamento de Matemáticas, Universidad de Guanajuato, Callejón Jalisco s/n, A.P. 402, C.P. 36000,
Guanajuato, Gto. México.
1
Índice
1. Introducción
1.1. Sobre las notas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2. Notación . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
4
5
2. Acciones en Variedades y Cocientes
5
3. La acción natural de un subgrupo finito en Cn
3.1. Grupos Reductivos . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
11
4. Cocientes de Variedades Afines
14
4.1. Conjugación de Matrices . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22
5. Cocientes de Variedades Proyectivas
25
5.1. Ejemplos en Variedades Proyectivas . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 27
6. Criterio de Hilbert-Mumford
6.1. Ejemplos que hacen uso del Criterio de Hilbert-Mumford
2
. . . . . . . . . . . . . . . . . . . .
30
32
1.
Introducción
Uno de los objetivos principales de la Teorı́a de Invariantes Geométricos (en inglés Geometric Invariant
Theory o GIT) es resolver problemas de clasificación de objetos en Geometrı́a Algebraica.
El antecedente de la Teorı́a de Invariantes Geométricos es la Teorı́a de Invariantes; sin embargo, no hay
que olvidar que esta teorı́a proviene también de problemas geométricos. Entre otros grandes autores podemos mencionar los trabajos hechos por David Hilbert en esta rama, dichos trabajos son aproximadamente
de 1890, podemos decir que sus resultados en esta área dieron origen a la teorı́a de ideales en anillos de
polinomios.
El problema fundamental en la teorı́a de invariantes es el siguiente: dada una acción “buena”de un grupo
G de automorfismos de un anillo de polinomios R, encontrar los elementos de R que quedan invariantes ante
la acción de G, estos elementos forman una subálgebra de R que denotaremos por RG . El objetivo esencial
es probar que RG es un álgebra finitamente generada y encontrar los generadores.
Ejemplo: Sea R = C[x1 , ..., xn ] y denotemos por Σn al grupo de permutaciones de {1, ..., n}. Tenemos la
siguiente acción:
C[x1 , ..., xn ] × Σn → C[x1 , ..., xn ]
(f (x1 , ..., xn ), σ) 7→ f (xσ(1) , ..., xσ(n) ).
El conjunto de invariantes RΣ = {f ∈ C[x1 , ..., xn ] : f (x1 , ..., xn ) = f (xσ(1) , ..., xσ(n) ) ∀σ ∈ Σ}, que en
este caso se llama el anillo de funciones simétricas, es un subanillo de R. Este subanillo contiene a las
funciones simétricas elementales:
f1 (x1 , ..., xn ) = x1 + · · · + xn
X
f2 (x1 , ..., xn ) =
xi xj
1≤i<j≤n
..
.
fn (x1 , ..., xn ) = x1 x2 · · · xn .
De hecho se prueba que RΣ está generado como C-álgebra por f1 , ..., fn , es decir, todo elemento de RΣ puede
escribirse de manera única como un polinomio en los fi . Ası́ que RΣ es isomorfo al anillo C[f1 , ..., fn ].
La Teorı́a de Invariantes Geométricos es la aplicación de la Teorı́a de Invariantes para construir objetos
geométricos que, a su vez, clasifican otros objetos. La TIG fue desarrollada por David Mumford en la década
de los sesentas del siglo pasado y gracias a ella Mumford fue galardonado con el máximo premio al que puede
aspirar un matemático a nivel mundial, la medalla Fields.
En términos generales el problema que plantea esta teorı́a es el siguiente: partimos de un conjunto X
donde viven los objetos que queremos clasificar y consideramos en este conjunto la acción de un grupo G:
G×X →X
(g, x) 7→ gx.
Tenemos entonces el conjunto de órbitas de la acción, a este conjunto lo denotaremos por X/G, y tenemos
también la aplicación proyección:
3
π : X → X/G
x 7→ O(x) = {gx : g ∈ G}.
Si X es un espacio topológico, entonces, definiendo los abiertos U en X/G como aquellos conjuntos tales
que π −1 (U ) es abierto en X, X/G es también un espacio topológico y π es una aplicación continua.
En el caso en que X es una variedad algebraica y G actúa de tal modo que en la órbita de un punto se
encuentren todos los objetos que deseamos identificar con él, uno esperarı́a que el conjunto de órbitas tuviera una estructura algebraica y que la aplicación proyección fuera también algebraica. En general esto no es ası́.
La Teorı́a de invariantes geométricos estudia los casos en que es posible construir espacios que clasifiquen los objetos en cuestión que a su vez sean variedades algebraicas, junto con un morfismo algebraico
de la variedad donde viven nuestros objetos a tal espacio. Como veremos más adelante, en general esto no
se consigue con el conjunto de órbitas en el que cada órbita serı́a un punto en el espacio clasificante, en
general vamos a tener el siguiente fenómeno: una órbita junto con las que se acumulen en ella representarán
el mismo punto en el cociente, al que por el momento llamaremos bueno (después precisaremos este concepto).
Podemos resumir lo anterior diciendo que el objetivo principal de TIG es resolver problemas de clasificación en geometrı́a algebraica, es decir, construir cocientes buenos cuyos puntos corresponden a clases de
isomorfismos (dadas por la acción) de los objetos a clasificar y con la ventaja de que dicho espacio refleje las
propiedades geométricas y algebraicas de los objetos que está clasificando.
1.1.
Sobre las notas
El prerrequisito recomendable para hacer una lectura eficiente de este escrito es haber tomado un curso básico de geometrı́a algebraica en el que el lector haya adquirido un conocimiento general de los que
son las variedades algebraicas (afines y proyectivas), ası́ como su anillo de funciones y los morfismos entre ellas; esto implica, en particular, tener un conocimiento general de álgebra conmutativa y topologı́a de
Zariski. En este apartado daremos un esquema general del modo en que se presentan los temas en estas notas.
Como ya hemos mencionado, nuestro objetivo general es dar una idea básica de la construcción de
cocientes con estructura algebraica por acciones de grupos en variedades algebraicas afines y proyectivas.
Empezaremos la exposición con las definiciones generales de acciones de grupos y cocientes bueno, categórico
y geométrico; esta parte puede resultar tediosa debido a la gran cantidad de conceptos que se introducen,
ası́ que la sección 3 tiene el objetivo de aclarar un poco estos conceptos mediante el ejemplo particular de
acciones en espacios afines por grupos finitos.
La siguiente sección pretende dar una idea panorámica de los que son los grupos reductivos, estos grupos
tienen la gracia de que al actuar linealmente en una variedad algebraica es posible obtener cocientes buenos
en un abierto invariante de dicha variedad.
A continuación daremos la demostración del teorema de Nagata que nos dice que el álgebra de invariantes
por la acción de un grupo reductivo resulta finitamente generada; y, como consecuencia importante, probaremos la existencia de un cociente bueno por la acción de un grupo reductivo en una variedad afı́n.
La siguiente sección expone un ejemplo clásico: la conjugación de matrices. Este ejemplo ilustra de manera clara lo que está pasando geométricamente con las órbitas cuando construimos cocientes por acciones
de grupos. El objetivo de esta sección es observar que, cuando las órbitas son cerradas, la construcción del
cociente es inmediata pero en el caso de órbitas que se acumulan en otras resultan hechos realmente sorpren-
4
dentes.
La siguiente meta es tratar de construir cocientes de variedades proyectivas por acciones de grupos reductivos, esto en general no es posible a menos que eliminemos un cerrado de la variedad, el cerrado constituido
por los llamados puntos inestables. El complemento de este cerrado es el abierto de puntos semiestables y
en este conjunto invariante sı́ podremos construir un cociente bueno.
Una vez que hemos entendido por qué los puntos inestables representan una obstrucción para construir
cocientes en variedades proyectivas, daremos algunos ejemplos en los que describimos dichos puntos, con ello
veremos que estos puntos son degenerados en algún sentido, por ahora, ambiguo.
Describiremos enseguida un método desarrollado por David Hilbert y por David Mumford para encontrar
los puntos inestables de una acción, este método hace uso de los subgrupos a un parámetro del grupo, ası́ que
le daremos este nombre. Terminaremos las notas con algunos ejemplos que muestran el poder del Método de
Subgrupos a un Parámetro descrito anteriormente.
1.2.
Notación
1. Todos los anillos mencionados en las notas serán conmutativos con 1.
2. K será un campo algebraicamente cerrado de cualquier caracterı́stica.
3. Denotaremos el espacio afı́n de dimensión n en el campo K por A(K)n y el espacio proyectivo de
dimensión n sobre K como P(K)n .
4. Sea X una variedad y sea U un abierto de X, entonces
A(U ) = {f : U → K : f es una función regular}.
5. Si R es un anillo y f ∈ R entonces Rf es la localización del anillo en f .
2.
Acciones en Variedades y Cocientes
A continuación daremos todas las definiciones generales para poder plantear de un modo general el problema que queremos estudiar, dichas definiciones incluyen la de grupo algebraico, acciones en variedades
algebraicas y, por supuesto, cocientes en geometrı́a algebraica.
Lo referente a grupos algebraicos que se menciona a continuación puede ser consultado en [2] y [19].
Definición 1. Un grupo G se dice algebraico sobre un campo K si es una variedad algebraica sobre K
y las operaciones de multiplicación e inverso son morfismos algebraicos. Un grupo algebraico isomorfo a un
subgrupo cerrado de GL(n, K) se dice grupo algebraico lineal.
Aquı́ es necesario hacer la siguiente observación: todos los grupos algebraicos que manejaremos en el texto
serán lineales, de hecho esta es la clase de grupos algebraicos que tienen estructura de variedad afı́n. La clase
de grupos algebraicos que tienen estructura de variedad proyectiva son las llamadas variedades abelianas, un
tema de estudio fascinante que no tocaremos aquı́.
Definición 2. Sean G1 y G2 grupos algebraicos, un homomorfismo de grupos algebraicos, es un homomorfismo de grupos φ : G1 → G2 , que es morfismo de variedades algebraicas.
5
Ejemplo 1. Los ejemplos clásicos de grupos algebraicos lineales son GL(n, K), SL(n, K), P GL(n, K) y
todo grupo finito, el cual, como sabemos, es subgrupo de un grupo de permutaciones Σn y por lo tanto es
subgrupo de GL(n, K).
Definición 3. Una acción de un grupo algebraico G en una variedad X es un morfismo
σ :G×X →X
tal que, para todo g1 , g2 ∈ G, x ∈ X,
σ(g1 , σ(g2 , x)) = σ(g1 g2 , x)
y
σ(e, x) = x,
donde e es el elemento identidad de G. Para simplificar la notación escribiremos gx para referirnos a σ(g, x),
ası́ que las condiciones anteriores se escriben:
g1 (g2 x) = (g1 g2 )x,
ex = x.
Sea x ∈ X. Definimos el estabilizador de x y la órbita de x como
Est(x) = {g ∈ G : gx = x}
O(x) = {gx ∈ X : g ∈ G},
respectivamente. Diremos que el conjunto W ⊂ X es invariante por la acción de G si gW = {gw : w ∈
W } ⊂ W para todo g ∈ G.
Ejemplo 2. La aplicación:
GL(n, K) × A(K)n → A(K)n
(g, (x1 , ..., xn )) 7→ g(x1 , ..., xn ),
que consiste simplemente en aplicar la transformación lineal g al punto (x1 , ..., xn ) es una acción, la órbita
de un punto distinto de cero es A(K)n − {0} y la órbita de cero es simplemente el cero.
Sea X una variedad afı́n en A(K)n+1 o proyectiva en P(K)n y sea G un grupo algebraico lineal. Supongamos que existe una acción
G×X →X
(g, x) 7→ gx,
de G sobre X.
Definición 4. La acción anterior se dice lineal o que G actúa linealmente sobre X si existe un homomorfismo de grupos
ρ : G → GL(n + 1, K)
tal que la acción de G en X es la acción inducida por
G × A(K)n+1 → A(K)n+1
(g, (x0 , ..., xn )) 7→ ρ(g)(x0 , ..., xn ),
donde ρ(g)(x0 , ..., xn ) es simplemente aplicar la transformación lineal ρ(g) en el punto (x0 , ..., xn ).
6
Ejemplo 3. La acción del ejemplo anterior es lineal.
El primer paso importante para llegar a la construcción de un cociente bueno de una variedad algebraica
por la acción de un grupo algebraico es considerar la acción inducida en el álgebra de funciones algebraicas
de la variedad. Dicha acción se describe a continuación, supongamos que el grupo algebraico lineal G actúa
en una variedad algebraica X, esta acción induce una acción en el álgebra de funciones de X, es decir en
A(X), de la siguiente manera:
A(X) × G → A(X)
(f, g) 7→ f g : X → K
x 7→ f (gx).
Definición 5. Un elemento f ∈ A(X) es invariante por la acción de G si f g (x) = f (x) para todo x ∈ X
y g ∈ G. Si W es un subconjunto abierto e invariante de X, definimos el conjunto A(W )G := {f ∈ A(W ) :
f g (x) = f (x) ∀x ∈ W, ∀g ∈ G}.
Ahora vamos a dar las definiciones de cociente bueno, cociente categórico y espacio de órbitas, cada uno
de ellos juega un papel importante en los problemas de clasificación que queremos entender.
Definición 6. Un cociente bueno de X por G es una pareja (Y, φ) donde Y es una variedad y φ : X → Y
es un morfismo afı́n que satisface las siguientes condiciones:
1. φ es G-invariante.
2. φ es sobre.
3. Si U es un abierto de Y , entonces
φ∗ : A(U ) → A(φ−1 (U ))
es un isomorfismo de A(U ) sobre A(φ−1 (U ))G .
4. Si W es un subconjunto invariante y cerrado de X, entonces φ(W ) es cerrado.
5. Si W1 , W2 son subconjuntos de X, cerrados, invariantes y disjuntos, entonces
φ(W1 ) ∩ φ(W2 ) = ∅.
Definición 7. Un cociente categórico de X por G es un par (Y, φ), donde Y es una variedad y φ : X → Y
es un morfismo tal que:
1. φ es constante en las órbitas de la acción.
2. Para cada variedad Y1 y morfismo φ1 : X → Y1 constante en órbitas, existe un único morfismo
χ : Y → Y1 tal que χ ◦ φ = φ1 . Es decir, el siguiente diagrama
/Y
~
~
~
φ1
~~
~~ ~ ∃!χ
Y1
X
φ
conmuta.
Si, además, φ−1 (y) consiste de sólo una órbita para todo y ∈ Y entonces (Y, φ) se llama espacio de órbitas.
7
Definición 8. Un cociente geométrico es un cociente bueno que es, además, un espacio de órbitas.
Todo cociente bueno es un cociente categórico, es decir, los cocientes buenos satisfacen una propiedad
universal. De hecho tenemos la siguiente proposición.
Proposición 1. (ver [15]) Sea (Y, φ) un cociente bueno de X por G. Entonces
1. (Y, φ) es un cociente categórico de X por G;
2. φ(x1 ) = φ(x2 ) si y sólo si O(x1 ) ∩ O(x2 ) 6= ∅;
3. si la acción de G en X es cerrada, es decir, si todas las órbitas son conjuntos cerrados, entonces (Y, φ)
es un cociente geométrico.
Las construcciones de cocientes que haremos en estas notas estarán basadas en el hecho de que A(X)G
sea finitamente generada como K-álgebra, es decir, que existan elementos f1 , ..., fs ∈ A(X)G tales que
A(X)G = K[f1 , ..., fs ], esto significa que toda función invariante se puede escribir como un polinomio en
f1 , ..., fs .
3.
La acción natural de un subgrupo finito en Cn
Lo primero que haremos para empezar a entender los conceptos que se presentaron en la sección anterior
es considerar el caso particular de acciones de grupos finitos en el espacio afı́n. El álgebra de funciones
polinomiales del espacio afı́n es el anillo de polinomios, ası́ que para la construcción del cociente bueno
introducimos los polinomios invariantes y estudiamos el álgebra de polinomios invariantes. Si dicha álgebra
resulta ser finitamente generada, lo cual en el caso de grupos finitos es cierto, entonces podremos construir
el cociente bueno, en este caso debemos destacar que el cociente bueno coincidirá con el conjunto de órbitas
debido a que todas las órbitas son conjuntos cerrados de la misma dimensión.
Recordemos que todo grupo finito es subgrupo de algún grupo de permutaciones Σn y, por tanto, es un
grupo algebraico lineal. Consideremos la acción natural del grupo finito G ⊂ GL(n, C) en el espacio afı́n
complejo An (C) (por comodidad vamos a denotar este espacio por Cn ):
G × Cn → Cn


x1


(g, (x1 , ..., xn )) 7→ g  ... ,
xn
lo que deseamos es construir un cociente bueno. El primer paso para hacer esta construcción es considerar
la acción inducida en el álgebra de funciones del espacio afı́n Cn que, como sabemos, es C[x1 , ..., xn ],
C[x1 , ..., xn ] × G → C[x1 , ..., xn ]
(f, g) 7→ f g : Cn → C
x 7→ f (gx).
Adaptando las definiciones de función invariante a este caso tenemos que un polinomio f ∈ C[x1 , ..., xn ]
es invariante bajo G si f (x) = f (gx) para todo g ∈ G y el conjunto de polinomios invariantes bajo G
será denotado por C[x1 , ..., xn ]G .
Emmy Noether demostró en [16] el siguiente importante resultado.
8
Teorema 1. C[x1 , ..., xn ]G es finitamente generado como C-álgebra, es decir, existen polinomios f1 , ..., fs ∈
C[x1 , ..., xn ] tales que C[x1 , ..., xn ]G = C[f1 , ..., fs ].
Un caso particular lo tenemos cuando el grupo en cuestión es Σn , en este caso se pueden construir
facilmente los generadores del álgebra de invariantes y en la demostración que damos enseguida, la cual se
puede encontrar en [3], se construye todo polinomio invariante como polinomio en los polinomios simétricos
elementales.
Teorema 2. Con la notación del ejemplo presentado en la introducción, tenemos que:
C[x1 , ..., xn ]Σn = C[f1 , ..., fn ].
Demostración. Usaremos en el conjunto de monomios el orden lexicográfico con x1 > x2 > ... > xn . Sea f
un polinomio simétrico no cero y sea T P (f ) = axα el término principal de f , es decir, el mayor término en
f . Lo primero que probaremos es que si α = (α1 , ..., αn ), entonces α1 ≥ α2 ≥ ... ≥ αn . Para probar esto,
supongamos que αi < αi+1 y sea β = (α1 , ..., αi+1 , αi , ..., αn ).
Como axα es un término de f , entonces axβ es un término de f (..., xi+1 , xi , ...). Pero como f es simétrico,
entonces f (..., xi+1 , xi , ...) = f y, por lo tanto, axβ también es un término de f . Pero esto es imposible, pues
xβ > xα . Hemos probado la afirmación.
Sea
α
n−1
h = f1α1 −α2 f2α2 −α3 · · · fn−1
−αn αn
fn ,
para calcular el término principal de h primero notemos que T P (fr ) = x1 x2 · · · xr para 1 ≤ r ≤ n. Ası́ que
α
n−1
T P (h) = T P (f1α1 −α2 f2α2 −α3 · · · fn−1
−αn αn
fn )
= T P (f1 )α1 −α2 T P (f2 )α2 −α3 · · · T P (fn−1 )αn−1 −αn T P (fn )αn
1 −α2
= xα
(x1 x2 )α2 −α3 · · · (x1 x2 · · · xn )αn
1
α
αn
1
= xα
1 · · · xn = x .
Se sigue, entonces que P
f y ah tienen el mismo término principal, y, entonces, si definimos el multigrado
de un polinomio F = α aα xα como multigrado(F ) = max{α ∈ Zn≥0 : aα 6= 0} (el máximo se toma
respecto al orden lexicográfico) multigrado(f − ah) < multigrado(f ), siempre que f − ah 6= 0.
Sea g1 = f − ah, notar que g1 es simétrico ya que f y h lo son. Si g1 6= 0, podemos repetir este proceso
para obtener g2 = g1 − a1 h1 , donde a1 es una constante y h1 es un producto de las funciones simétricas
elementales, f1 , ..., fn con alguna potencia. Y sabemos que T P (g2 ) < T P (g1 ) cuando g2 6= 0. Continuando
de esta manera obtenemos una sucesión de polinomios f, g1 , g2 , ... con
multigrado(f ) > multigrado(g1 ) > multigrado(g2 ) > ...
Esta suceción debe ser finita. Esto significa que el proceso termina y entonces gt+1 = 0 para algún t. Ası́ que
f = ah + a1 h1 + ... + at ht ,
lo cual prueba que f es un polinomio en las funciones simétricas elementales.
Ejercicio 1. Demuestra que un polinomio simétrico puede escribirse de manera única como un polinomio
en las funciones simétricas elementales f1 , ..., fn . Concluye con esto que C[x1 , ..., xn ]Σn es isomorfo como
C-álgebra a C[x1 , ..., xn ].
9
Regresando al caso general tenemos, gracias al teorema de Emmy Noether, que existen polinomios
f1 , ..., fs ∈ C[x1 , ..., xn ] tales que C[x1 , ..., xn ]G = C[f1 , ..., fs ] y si consideramos el ideal I = {h ∈ C[y1 , ..., ys ] :
h(f1 , ..., fs ) = 0 en C[x1 , ..., xn ]}, entonces la correspodencia
ϕ : Cn /G → Y
O(x) 7→ (f1 (x), ..., fs (x)),
donde Y es la variedad definida por I, es decir, Y = {(a1 , ..., as ) ∈ A(C)s : h(a1 , ..., as ) = 0 ∀h ∈ I}; es una
biyección (la demostración de este hecho puede encontrarse en el Teorema 10 del capı́tulo 4 de [3]), donde
Cn /G = {O(x) : x ∈ Cn }. Esto se debe principalmente a que la órbita de un punto es un conjunto finito y,
por tanto, es un conjunto cerrado y de hecho todas las órbitas tienen la misma dimensión. Esta condición
es muy fuerte y nos permite hacer construcciones de cocientes con hermosas propiedades; el ejemplo de las
matrices que se presenta en una sección posterior nos ayudará a entender la geometrı́a del cociente cuando
las órbitas tienen en su cerradura otras órbitas.
Consideramos entonces la aplicación proyección seguida de la aplicación ϕ:
φ = ϕ ◦ π : Cn → Cn /G → Y
x 7→ O(x) 7→ (f1 (x), ..., fs (x));
como ya hemos mencionado en la introducción, con la aplicación proyección podemos darle una topologı́a a
Cn /G del siguiente modo: un conjunto U ⊂ Cn /G es abierto si y sólo si π −1 (U ) es abierto en Cn . Podemos
identificar las funciones continuas de Cn /G a C con el álgebra de invariantes C[x1 , ..., xn ]G . Entonces la
aplicación φ induce el siguiente morfismo de anillos:
φ∗ : A(Y ) = C[y1 , ..., ys ]/I → C[x1 , ..., xn ]G = C[f1 , ..., fs ] → A(Cn ) = C[x1 , ..., xn ]
h(y1 , ..., ys ) + I = h̄(y1 , ..., ys ) 7→ h(f1 , ..., fn ) 7→ h(f1 (x1 , ..., xn ), ..., fs (x1 , ..., xn )).
Y tenemos el siguiente Teorema.
Teorema 3. La aplicación φ : Cn → Y es un cociente bueno de Cn por G. Más aun, este cociente es
geométrico.
Demostración. La aplicación:
φ : Cn → Y
x 7→ (f1 (x), ..., fs (x)),
es claramente afı́n e invariante en las órbitas. La condición 2 de la definición 6 se sigue del hecho que ϕ es
sobre. Para demostrar la condición 3 vamos a usar el resultado que nos dice que todo abierto de Y puede
ser cubierto por los abiertos Yh̄ = {y ∈ Y : h̄(y) 6= 0}, donde h̄ ∈ A(Y ); ası́ que demostraremos el resultado
para estos abiertos:
φ∗ (A(Yh̄ )) = φ∗ (A(Y )h̄ ) = π ∗ (C[x1 , ..., xn ]G
h(f1 ,...,fs ) ) =
(π ∗ (C[x1 , ..., xn ]G ))h(f1 (x1 ,...,xn ),...,fs (x1 ,...,xn )) = C(x1 , ..., xn )G
h(f1 ,...,fs ) =
A(Cnh(f1 (x1 ,...,xn ),...,fs (x1 ,...,xn )) )G = A(φ−1 (Yh̄ ))G ,
10
la inyectividad se sigue de la definición de φ∗ . Podemos ver que φ es un morfismo finito y, por tanto, es un
morfismo cerrado, de aquı́ se sigue la condición 4.
Sean W1 , W2 subconjuntos de Cn , cerrados, invariantes y disjuntos; supongamos que y ∈ φ(W1 ) ∩ φ(W2 ),
es decir, existen a ∈ W1 y b ∈ W2 tales que fj (a) = fj (b) para todo j = 1, ..., s, entonces tenemos que para
todo h, polinomio invariante por G, h(a) = h(b).
Como O(a) y O(b) son conjuntos cerrados disjuntos de Cn entonces existe un polinomio f ∈ C[x1 , ..., xn ]
tal que f|O(a) ≡ 1 y f|O(b) ≡ 0; consideremos el polinomio:
hf =
1 X g
f
|G|
∈ C[x1 , ..., xn ],
g∈G
es fácil ver que hf es un polinomio invariante, y hf (a) = 1, hf (b) = 0, lo cual es una contradicción. Hemos
probado que φ(W1 ) ∩ φ(W2 ) = ∅. Y con esto concluimos que φ : Cn → Y es un cociente bueno.
Todas las órbitas de esta acción son conjuntos cerrados, ası́ que, por la proposición 1, este cociente es
geométrico.
Vamos a finalizar esta sección con algunos ejemplos sencillos de lo que hemos expuesto hasta ahora.
Ejemplo 4. Hemos demostrado que C[x1 , ..., xn ]Σn = C[f1 , ..., fn ] donde f1 , ..., fn son las funciones simétricas elementales y, por el ejercicio 1 tenemos que I = {h ∈ C[y1 , ..., yn ] : h(f1 , ..., fn ) = 0 en C[x1 , ..., xn ]} =
{0}, ası́ que el cociente bueno de la acción natural de Σn en Cn es:
φ : Cn → Cn
(x1 , ...., xn ) 7→ (f1 (x1 , ..., xn ), ..., fn (x1 , ...., xn )).
Ejemplo 5. Consideremos el grupo cı́clico:
−1 0
1
C2 =
,
0 −1
0
0
1
⊂ GL(2, C).
Podemos probar que C[x1 , x2 ]C2 = C[x21 , x22 , x1 x2 ] y I = {h ∈ C[y1 , y2 , y3 ] : h(x21 , x22 , x1 x2 ) = 0 en C[x1 , ..., xn ]} =<
y1 y2 − y32 >, ası́ que el cociente bueno está dado por:
φ : C2 → Y = {(y1 , y2 , y3 ) ∈ C3 : y1 y2 = y32 }
(x1 , x2 ) 7→ (x21 , x22 , x1 x2 ).
3.1.
Grupos Reductivos
De acuerdo a lo expuesto en la sección anterior podemos intuir que la generación finita del álgebra de
invariantes nos permite construir cocientes de variedades por acciones de grupos algebraicos lineales pero,
¿todo grupo algebraico lineal satisface esta propiedad? ¿cuáles son los grupos algebraicos lineales que hacen
del álgebra de invariantes un álgebra finitamente generada? En esta sección vamos a dar las definiciones
y resultados básicos sobre la clase de grupos que tienen esta importante propiedad, dichos grupos son los
grupos reductivos.
En el Congreso Internacional de Matemáticas, celebrado en Paris en 1900, David Hilbert propuso una
lista de 23 problemas que marcarı́an gran parte del desarrollo de las matemáticas del siglo pasado. El problema 14 planteaba, entre otras cosas, lo que hemos venido mencionando sobre la generación finita del álgebra
11
de invariantes, Hilbert demostró que esto era ası́ en algunos casos particulares.
El estudio de los grupos con esta propiedad atrajó y sigue atrayendo a muchı́simos matemáticos importantes que han contribuido al desarrollo de la teorı́a, entre ellos podemos mencionar a Masayoshi Nagata,
quien en el año 1958 presentó el primer contraejemplo al problema catorce de Hilbert (ver [14]), es decir, construyó un álgebra finitamente generada y un grupo actuando en ella de tal modo que el álgebra de invariantes
no era finitamente generada (el lector interesado en este tema puede encontrar una buena introducción en
[18]).
En 1963 Masayoshi Nagata demostró la generación finita del álgebra de invariantes para los grupos
geométricamente reductivos (ver [13]), la demostración de este importante Teorema se verá en la siguiente
sección. Por ahora introducimos los conceptos de grupo geométricamente reductivo y grupo linealmente
reductivo.
Definición 9. Un grupo algebraico lineal G se dice geométricamente reductivo (linealmente reductivo) si, para cada acción lineal de G en A(K)n , y cada punto v ∈ A(K)n , v 6= 0, invariante por la acción
de G, exite f ∈ C[x1 , ..., xn ], homogéneo, invariante, de grado mayor o igual a uno (igual a uno) tal que
f (v) 6= 0.
Ejemplo 6. Todo grupo finito G es geometricamente reductivo: consideremos una acción lineal de G en
A(K)n y sea v ∈ A(K)n , v P
6= 0, invariante por la acción de G, existe f polinomio homogéneo tal que
1
g
G
f (v) = 1, entonces f G = |G|
g∈G f es invariante, homogéneo y f (v) = 1.
Ejemplo 7. El grupo aditivo Ga , es decir, el grupo cuyos elementos son los elementos del campo K con la
suma, no es geometricamente reductivo. Este grupo puede verse como un subgrupo de GL(2, K) del siguiente
modo:
1 a
Ga =
∈ GL(2, K) : a ∈ K ;
0 1
consideremos la acción natural de Ga en A(K)2 , es decir,
1
0
Ga × A(K)2 → A(K)2
a
, (x1 , x2 ) 7→ (x1 + ax2 , x2 ),
1
el punto (1, 0) es invariante por Ga . Supongamos que el grupo es geometricamente reductivo, entonces existe
un polinomio mónico e invariante f (x1 , x2 ) = a0 xr2 + a1 x1 x2r−1 + ... + xr1 . Como f es invariante por Ga
entonces f (x1 , x2 ) = f (x1 + ax2 , x2 ) para todo a ∈ K, y esto implica que a0 = a0 + a1 a + ... + ar−1 ar−1 + ar
para todo a ∈ K, lo cual es una contradicción pues un polinomio tiene un número finito de raices.
Ahora introducimos el concepto de grupo reductivo, en 1963 Masayoshi Nagata y Miyata en el artı́culo[11]
probaron que todo grupo geométricamente reductivo es reductivo, ası́ que, en principio se tenı́a la generación
finita del álgebra de invariantes para un tipo especial de grupos reductivos.
Definición 10. Sea G un grupo algebraico lineal, un elemento u ∈ G se dice unipotente si existe un entero
r tal que (u − Id)r = 0, donde Id es la matriz identidad. El grupo G se llama unipotente si todos sus
elementos son unipotentes.
Ejemplo 8. El grupo aditivo Ga es unipotente pues la matriz:
1
0
a
1
−
1
0
0
1
es nilpotente para todo a 6= 0.
12
=
0
0
a
0
Definición 11. Sea G un grupo algebraico lineal, denotaremos por Gu el subgrupo maximal, normal, unipotente de G. El radical unipotente de G denotado por Ru (G) es la componente conexa de la identidad
en Gu .
Definición 12. Un grupo algebraico lineal G es reductivo si es conexo y Ru (G) = {Id}
Ejemplo 9. El toro algebraico de dimensión n, es decir, (K ∗ )n es reductivo. Si u = (u1 , ..., un ) ∈ (K ∗ )n
es unipotente entonces existe un entero r tal que (uj − 1)r = 0 para todo j = 1, ..., n, y esto implica que
uj = 1 para todo j = 1, ..., n, ası́ que Ru ((K ∗ )n ) = {(1, ..., 1)}. Obviamente el toro algebraico de dimensión
n es el subgrupo de matrices diagonales de GL(n, K).
Ejemplo 10. Los grupos GL(n, K), SL(n, K), P GL(n, K), ası́ como los subgrupos finitos de GL(n, K) son
reductivos, la demostración completa de este hecho puede consultarse en [19]. Aquı́ vamos a demostrar con
detalle la reductividad para el grupo GL(2, K). Supongamos que existe u ∈ Ru (GL(2, K)) distinto de la
identidad, entonces u es conjugada a una matriz de la forma:
u0 =
1
0
a
1
,
con a 6= 0, como Ru (GL(2, K)) es normal entonces u0 ∈ Ru (GL(2, K)) y:
1
a
1
0
0
a
1 0
0 a
1 0
1
puesto que la matrix
es conjugada de
1 1
0
Ru (GL(2, K)), lo cual es una contradicción pues:
1
0
a
1
2
1
1
0
−
1
0
−1
=
1
1
0
1
1
0
1
1
∈ Ru (GL(2, K)),
tenemos que
2
=2
1
0
0
1
1
0
1
1
1
1
0
1
=
2
1
1
0
∈
.
Ejemplo 11. Evidentemente ningún grupo unipotente, conexo no trivial es reductivo, tal es el caso de Ga .
Ejemplo 12. El subgrupo de GL(4, C) definido por

1 b c bc



0 1 0 c
G= 
 0 0 a ab



0 0 0 a






 : a ∈ C∗ , b, c ∈ C




no es reductivo. Consideremos el subgrupo U de G definido por la condición a = 1, entonces U es un subgrupo
algebraico lineal de G, se deja al lecto probar que U es abeliano y conexo. Sean:

1
 0
g=
 0
0
b
1
0
0
c
0
a
0

bc
c 
∈G
ab 
a

1
 0
u=
 0
0
β
1
0
0
γ
0
1
0

βγ
γ 
 ∈ U,
β 
1
entonces

gug −1
1
 0
=
 0
0
β
1
0
0
a−1 γ
0
1
0
13

a−1 βγ
a−1 γ 
 ∈ U,

β
1
ası́ que U es normal, y claramente sus elementos son unipotentes. Por lo tanto U ⊂ Ru (G) y concluimos
que G no es reductivo.
En 1939 el matemático alemán Hermann Klaus Hugo Weyl habı́a probado que en campos de caracterı́stica
cero todo grupo reductivo es linealmente reductivo (ver [21]). Con todos estos resultados llegamos al siguiente
Teorema.
Teorema 4. Sea G un grupo algebraico lineal sobre un campo K de caracterı́stica cero. Entonces lo siguiente
es equivalente:
1. G es reductivo
2. G es linealmente reductivo
3. G es geométricamente reductivo.
Para campos de caracterı́stica arbitraria tenemos que William Haboush en [5] demostró, diez años después
de haber sido propuesta, la famosa Conjetura de Mumford, establecida en 1964, está conjetura decı́a que
todo grupo reductivo es geométricamente reductivo. Se tiene entonces el siguiente:
Teorema 5. Sea G un grupo algebraico lineal sobre un campo K. Entonces lo siguiente es equivalente:
1. G es reductivo
2. G es geométricamente reductivo.
La conclusión es que los grupos reductivos en campos algebraicamente cerrados de cualquier caracterı́stica
hacen del álgebra de invariantes un álgebra finitamente generada. De hecho esta clase de grupos es la más
grande con esta propiedad, en el siguiente sentido: Vladimir Popov probó en [17] que si un G grupo tiene la
propiedad de que para toda álgebra finitamente generada y toda acción lineal de G en el álgebra, el álgebra
de invariantes es finitamente generada entonces G es reductivo.
4.
Cocientes de Variedades Afines
Empezaremos esta sección dando la definición de acción racional en una K-álgebra. Como veremos más
adelante, toda acción lineal de un grupo algebraico en una variedad afı́n induce una acción racional en su
álgebra de funciones regulares; por otro lado, el teorema de Nagata nos garantiza la generación finita del
álgebra de invariantes bajo la acción racional de un grupo reductivo en un álgebra finitamente generada.
Definición 13. Sea G un grupo algebraico y R una K-álgebra. Una acción racional de G en R es una
aplicación
R×G→R
(f, g) 7→ f g ,
que satisface las siguientes propiedades:
1. Para todo f ∈ R y g1 , g2 ∈ G, f g1 g2 = (f g1 )g2 y f e = f .
2. Dado g ∈ G, la aplicación f 7→ f g es un automorfismo de K-álgebras de R.
3. Para cada elemento f ∈ R existe un subespacio vectorial de R de dimensión finita n, el cual contiene a
f , es invariante bajo G y sobre el cual G actúa mediante un morfismo de grupos algebraicos G → GL(n).
14
En el caso en que X es una variedad afı́n y actúa en ella un grupo reductivo G, el siguiente Teorema,
demostrado por Masayoshi Nagata en 1964 (ver [13]), tiene como consecuencia la existencia de una variedad
afı́n cuyos puntos en un abierto parametrizan a las órbitas cerradas y en el resto tenemos puntos que parametrizan cerraduras de órbitas tal que en ellas se acumulan órbitas de dimensión menor; además existe un
morfismo algebraico de X a esta variedad afı́n invariante en órbitas y con otras propiedades análogas a las
de la aplicación proyección.
El Teorema fue demostrado originalmente para grupos geometricamente reductivos, después fue demostrada la equivalencia de estos con los reductivos, enunciaremos el Teorema para estos últimos. Nosotros
presentaremos la demostración de este Teorema debido a la riqueza algebraica que contiene pero quien lo
desee puede omitir su lectura ya que ésta no es importante para entender las ideas que se presentan en el
resto de la exposición.
Teorema 6. (ver Teorema 3.4 de [15]) Sea G un grupo reductivo actuando racionalmente en una K-álgebra
finitamente generada A. Entonces AG = {f ∈ A : f g = f ∀g ∈ G} es finitamente generada como K-álgebra.
Demostración. Para la demostración de este teorema usaremos los siguientes lemas sobre K-álgebras que no
demostraremos aquı́, pero una buena referencia para consultar estas demostraciones es [4].
L
Lema 1. Sea A =L i≥0 Ai una K-álgebra graduada. Entonces A es finitamente generada como K-álgebra
si y sólo si A+ = i>0 Ai es finitamente generado como un ideal en A.
Lema 2. Sea A una K-álgebra finitamente generada, entera sobre una subálgebra B. Entonces A es un
B-módulo finito y B es finitamente generada como K-álgebra.
Lema 3. Sea A una K-álgebra, entera sobre una subálgebra B. Supongamos que A es un dominio y que el
campo de fracciones L de A es una extensión finitamente generada de K (i.e. existen elemento v1 , ..., vn ∈ L
tales que L = K(v1 , ..., vn ) ). Si B es una K-álgebra finitamente generada, entonces A es un B-módulo finito,
y entonces es una K-álgebra finitamente generada.
Lema 4. Consideremos las siguientes extensiones de campos K ⊂ L ⊂ K1 y supongamos que K1 es una
extensión finitamente generada de K. Entonces L es una extensión finitamente generada de K.
Ahora vamos a probar el siguiente lema de Nagata, fundamental en la prueba del Teorema. Supongamos
que G es un grupo reductivo actuando racionalmente en una K-álgebra R finitamente generada.
Lema 5. Sea J un ideal de R, invariante por G. Si h + J ∈ (R/J)G , entonces ht + (J ∩ RG ) ∈ RG /(J ∩ RG )
para algún entero positivo t.
Observación 1. Tenemos que ver a RG /(J ∩ RG ) como una subálgebra de (R/J)G mediante el homomorfismo de K-álgebras
φ : RG /(J ∩ RG ) → (R/J)G
h + (J ∩ RG ) 7→ h + J,
cuyo núcleo es J ∩ RG . Entonces este lema lo que está probando es que (R/J)G es entero sobre RG /(J ∩ RG ).
Demostración. Sea h ∈ R, podemos suponer que h ∈
/ J, pues si h + J = J el resultado es trivial. Tenemos
que probar que existen h0 ∈ RG y un entero positivo t tales que h0 − ht ∈ J, pues de esta manera tendrı́amos
que h0 + (J ∩ RG ) = ht + (J ∩ RG ).
Como G actúa racionalmente sobre R, el subespacio M de R generado por el conjunto {hg : g ∈ G} es
de dimensión finita, ya que si Wh es el subsepacio de dimensión finita e invariante que existe para h, por la
definición de racionalidad, entonces < hg : g ∈ G >⊂ Wh . Y claramente M es G-invariante.
15
Sea N = M ∩ J. Por hipótesis h ∈
/ J, entonces h ∈
/ N , pero hg − h ∈ N , ya que, debido a que f es
g
invariante por G, tenemos que h − h ∈ J, para todo g ∈ G.
Si {h2 , ..., hr } es una base del espacio vectorial N , entonces
{h, h2 , ..., hr } es una
P
P base de M . Veamos primero que son linealmente independientes sobre K: λh + λi hi = 0 implica
que
λi hi = −λh ∈ J, ası́ que
Pr
λ = 0 y λi = 0 para todo i. Y, puesto que, para todo g ∈ G, hg − h = i=2 λi hi , entonces {h, h2 , ..., hr }
genera a M .
Entonces dim M = dim N + 1 y todo elemento de M puede escribirse de manera única como ah + h0 , con
a ∈ K, h0 ∈ N . Definimos entonces la siguiente aplicación lineal L : M → K, ah + h0 7→ a, esta aplicación
lineal es G invariante, ya que (ah + h0 )g = ah + a(hg − h) + h0g ∈ ah + N .
Sea M ∗ el espacio dual de M . Identifiquemos a M ∗ con K r con la base dual {h∗ , h∗2 , ..., h∗r }, entonces el
elemento L corresponde a (1, 0, ..., 0) ∈ K r . Más aún, L es invariante respecto a la acción lineal de G en K r
inducida por la acción dada en M .
Gracias a que G es geométricamente reductivo existe un polinomio F ∈ K[x1 , ..., xr ], homogéneo, invariante, de grado t ≥ 1 tal que F (L) 6= 0. Y esto implica que el coeficiente de xt1 en F es distinto de cero;
supondremos que este coeficiente es 1.
Finalmente consideramos el siguiente homomorfismo de K-álgebras
χ : K[x1 , ..., xr ] → R
x1 7→ h
xi 7→ hi
(i ≥ 2).
Se ve fácilmente que este homomorfismo conmuta con la acción de G en K[x1 , ..., xr ] y en R.
Tenemos que χ(F (x1 , ..., xr )) = F (h, h2 , ..., hr ) = h0 ∈ RG , ya que F es invariante; y h0 − ht pertenece
al ideal generado por h2 , ...hr el cual está contenido en J
Regresemos ahora a la demostración del Teorema de Nagata. Como R es finitamente generada como Kálgebra y G actúa racionalmente en R, entonces existen elementos f1 , ..., fm ∈ R linealmente independientes
sobre K tales que:
1. R = K[f1 , ..., fm ].
2. El subespacio vectorial de R generado
por f1 , ..., fm es invariante por G, y la acción de G en este
Pm
subespacio está dada por fig = j=1 αij (g)fj , donde G → GL(m, K), g 7→ αij (g), es un homomorfismo
de grupos algebraicos.
Esto se debe a que si Wfi es el subespacio vectorial de dimensión finita, invariante,
Sn que contiene a fi , el
cual existe gracias a que G es geométricamente reductivo, entonces W =< f : f ∈ i Wfi > es invariante y
< f1 , ..., fn >⊂ W .
g
PmSea S = K[x1 , ..., xm ]. Podemos ver que existe una única acción racional de G en S tal que xi =
j=1 αij (g)xj , para 1 ≤ i ≤ m y g ∈ G. Ası́ que tenemos una acción de G en R y en S y el homomorfismo
de K-álgebras φ : S → R, xi 7→ fi , conmuta con la acción, es decir, el siguiente diagrama:
16
/S
G×S
IG ×φ
φ
/ R,
G×R
conmuta. Esto, en particular, implica que si F ∈ Ker(φ) y g ∈ G, entonces F g ∈ Ker(φ), pues, para 0 ∈ R,
tenemos que 0g = 0. Entonces es suficiente probar el siguiente:
Teorema 7. Sea G un grupo algebraico lineal actuando racionalmente en S de tal manera que preserva
el grado de todo elemento homogéneo, y sea Q un ideal de S invariante por G. Entonces, para la acción
inducida en R = S/Q, RG es finitamente generada.
Demostración. Consideremos la acción de G en S y supongamos que existe un ideal homogéneo Q de S
invariante por G tal que RG = (S/Q)G no es finitamente generada.
Como S es un anillo Noetheriano podemos suponer que Q es un ideal maximal entre los ideales con
esta propiedad. Como Q es homogéneo, entonces R es también una K-álgebra graduada. Si J es un ideal
homogéneo, invariante de R, entonces J = J1 /Q, donde J1 es un ideal, homogéneo, invariante de S y Q ⊂ J1 ,
ası́ que, por la maximalidad de Q, tenemos que (R/J)G = ((S/Q)/(J1 /Q))G = (S/J1 )g es finitamente generada.
Por el lema 5, concluimos que (R/J)G es entero sobre RG /(J ∩ RG ) y, por el lema 2, tenemos que
RG /(J ∩ RG )
es finitamente generada
(1)
más aún
(R/J)G es un RG /(J ∩ RG )-módulo finito.
(2)
G
Sea f un polinomio homogéneo no constante en R . Si f no es un divisor de cero en R entonces afirmamos
que f R∩RG = f RG , ya que, como RG ⊂ R y f es invariante, entonces la contención f RG ⊂ RG ∩f R es clara
y sea f h ∈ RG , donde h ∈ R, entonces para todo g ∈ G, (f h)g = f g hg = f hg = f h, ası́ que f (hg − h) = 0,
por tanto, h ∈ RG .
Entonces, si consideramos el ideal J = f R de R, el cual es homogéneo e invariante porque f lo es, tenemos,
por la ecuación (1) y por la igualdad anterior, que RG /f RG es finitamente generada y, por el lema 1, concluiG
/f RG ,
mos que (RG /f RG )+ , es finitamente generado como ideal de RG /f RG . Y como (RG /f RG )+ = R+
G
G
entonces R+ es finitamente generado como ideal de R . Esto implica, nuevamente por el lema 1, que RG es
finitamente generada como álgebra, lo cual es una contradicción.
Para terminar la parte de la demostración en la que Q es homogéneo resta considerar el caso en el que
f es divisor de cero, es decir, el ideal I = {h ∈ R : f h = 0} =
6 {0}. Sea g ∈ G y
Psea h ∈ I, entonces
f hg = (f h)g = 0, ası́ que I es invariante.
Además
el
ideal
I
es
homogéneo,
pues
si
hi ∈ I, donde hi es
P
homogéneo de grado i, entonces
f hi = 0 implica que f hi = 0, pues f es homogéneo. Por tanto, por la
ecuación (1), las álgebras
RG /(f R ∩ Rg )
y
RG /(I ∩ Rg ),
son finitamente generadas. Ası́ que existe una subálgebra R1 de RG , finitamente generada, tal que los
homomorfismos naturales
17
R1 → RG /(f R ∩ Rg )
R1 → RG /(I ∩ Rg )
r1 7→ r1 + (f R ∩ Rg )
r1 7→ r1 + (I ∩ Rg ),
son sobre. Si RG /(f R∩Rg ) = K[a1 , ..., as ] y RG /(I∩Rg ) = K[b1 , ..., bn ], entonces R1 = K[a1 , ..., as , b1 , ..., bn ].
Notar que, por la ecuación (2), tenemos que (R/I)G es un RG /(I ∩ RG )-módulo finito. Sean c1 , ..., cr
elementos de R cuyas imágenes en R/I generan este módulo.
Para todo g ∈ G, tenemos (f ci )g = f g cgi = f cgi = f ci , ya que cgi −ci ∈ I. Ası́ que f ci ∈ RG . Hemos probado
que R1 [f c1 , ..., f cr ] ⊂ RG . Sea h ∈ RG , entonces existe h1 ∈ R1 tal que h1 + (f R ∩ Rg ) = h + (f R ∩ Rg ), es
decir, h − h1 = f b, para algún b ∈ R. Ası́ que
0 = (f b)g − f b = f (bg − b);
es P
decir, la imagen de b en R/I es invariante
bajo G. Se sigue que existen f1 , ..., fr ∈ R1 tales que
P
b− fi ci ∈ I. Por tanto h = h1 +f b = h1 + f fi ci ∈ R1 [f c1 , ..., f cr ]. Concluimos que R1 [f c1 , ..., f cr ] = RG ,
por tanto, RG es finitamente generada, y esto es una contradicción.
Ahora vamos a analizar el caso general. Supongamos que Q es un ideal maximal, invariante en S tal que
RG = (S/Q)G no es finitamente generada. Si RG contiene un divisor de cero, obtenemos una contradicción
usando el caso homogéneo. Supongamos, entonces, que RG es un dominio entero.
Por el caso homogéneo tenemos que S G es finitamente generada, y, por el lema 5 tenemos que: RG es
entero sobre S G /(Q ∩ S G ). Ası́ que, en vista del lema 3, es suficiente probar que el campo de fracciones L
de RG es una extensión finita de K.
Para esto, sea T = {r ∈ R : r no es divisor de cero en R}. Claramente T es un subconjunto multiplicativo de R. Sabemos que R ⊂ RT y, como RG es un dominio, entonces M ∩ RG = {0} para todo ideal propio
M de RT .
Si M es un ideal maximal, entonces L puede ser identificado con un subcampo de RT /M . Por el lema 4,
es suficiente probar que RT /M es una extensión finita de K. Pero esto es consecuencia de que RT /M es el
campo de fracciones de R/(M ∩ R), que es una K-álgebra finitamente generada.
Ahora procederemos a aplicar este Teorema para la construcción del cociente bueno en variedades afines,
para ello consideremos la siguiente acción lineal de un grupo reductivo G en una variedad afı́n X que vive
en A(K)n y definida por el ideal I ⊂ K[x1 , ..., xn ]:
G×X →X
(g, x) 7→ gx,
como lo hemos venido mencionando, esta acción induce una acción en el anillo de funciones regulares o anillo
coordenado de X:
A(X) = K[x1 , ..., xn ]/I × G → A(X)
(f, g) 7→ f g : X → K
x 7→ f (gx).
18
Como A(X) es finitamente generada, entonces, si G actúa racionalmente en A(X), tendrı́amos, por el Teorema de Nagata, que A(X)G es finitamente generada, es decir, existen f1 , ..., fs ∈ AG (X), tales que AG (X) =
K[f1 , ..., fs ]. Como K[f1 , ..., fs ] = K[y1 , ..., yn ]/J, donde J = {h ∈ K[y1 , ..., ys ] : h(f1 , ..., fs ) ≡ 0 en K[x1 , ..., xn ]},
entonces la variedad afı́n Y ⊂ A(K)s definida por J tiene como anillo coordenado al álgebra de invariantes
AG (X) y el morfismo de anillos:
φ∗ : A(Y ) = K[y1 , ..., yn ]/J → A(X)
h + J 7→ h(f1 , ..., fs ),
induce un morfismo algebraico φ : X → Y . En el Teorema 8 probaremos que (φ, Y ) es un cociente bueno.
Teorema 8. (ver pag. 61 de [15]) Sea G un grupo reductivo actuando en una variedad afı́n X, entonces
existe una variedad afı́n Y y un morfismo φ : X → Y tal que
1. φ es G − invariante, es decir, φ(gx) = φ(x) para todo g ∈ G.
2. φ es sobre.
3. Si U ⊂ Y es abierto entonces
φ∗ : A(U ) → A(φ−1 (U ))
f 7→ f ◦ φ
es un isomorfismo sobre A(φ−1 (U ))G .
4. Si W1 y W2 son subconjuntos invariantes, cerrados, disjuntos, entonces φ(W1 ) ∩ φ(W2 ) = ∅.
5. Si W es un subconjunto invariante, cerrado de X, entonces φ(W ) es cerrado.
Es decir, (Y, φ) es un cociente bueno.
Para la demostración del Teorema necesitaremos los siguientes lemas.
Lema 6. Sea G un grupo
en una K-álgebra R, finitamente generada. Si
P reductivo actuando racionalmente
P
f1 , ..., fs ∈ RG y f ∈ ( fi R) ∩ RG , entonces f t ∈
fi RG para algún entero positivo t.
Demostración. Demostraremos el lema usando inducción en s. Para s = 1, sea f ∈ f1 R ∩ RG ; entonces
f = f1 f ∗ y f1 (f ∗g − f ∗ ) = 0. Aplicando el lema 5 al ideal J = {h ∈ R : f1 h = 0}, obtenemos f ∗∗ ∈ RG y un
entero positivo t tales que f1 (f ∗∗ − f ∗t ) = 0. Ası́ que f t = f1t f ∗t = f1t f ∗∗ ∈ f1 RG .
Supongamos
ahora que s > 1. Sea R̄ = R/(f1 R) y sea f¯ la imagen de f ∈ R en R̄. P
Ası́ que si
P
s
f ∈ ( fi R) ∩P
RG , obtenemos, por hipótesis de inducción, un entero positivo t tal que f¯t ∈ i=2 f¯i R̄G .
s
t
G
Entonces f = i=0 fi hi , donde hi ∈ R y h¯2 , ..., h¯s ∈ R̄ .
Aplicamos ahora el lema 5 al ideal J = f1 R y obtenemos un entero positivo u y un elemento h∗s ∈ RG
Ps−1
tales que h̄us = h¯∗ s . Se sigue que f tu − fsu h∗s ∈ ( i=1 f1 R) ∩ RG .
Aplicando nuevamente la hipótesis de inducción, obtenemos un entero positivo v tal que (f tu − fsu h∗s )v ∈
Ps−1
Ps
G
tuv
∈ i=1 fi RG .
i=1 fi R . Por lo tanto f
El siguiente lema nos garantiza que toda acción lineal de un grupo algebraico G sobre una variedad X,
induce una acción racional de G sobre A(X).
19
Lema 7. Sea G un grupo algebraico lineal actuando en una variedad X, y sea W un subespacio vectorial de
A(X) de dimensión finita sobre K. Entonces
1. si W es invariante, la acción de G sobre W es lineal, y
2. en cualquier caso, W está contenido en un subespacio de A(X), de dimensión finita, invariante por la
acción de G.
Demostración. Sea W un subespacio vectorial de A(X), invariante por la acción de G, supongamos que
{f1 , ..., fn } es una base de este espacio. Podemos entonces escribir de manera única
fig =
n
X
ρij (g)fj ,
(3)
j=1
con ρij (g) ∈ K. Podemos ver fácilmente que la aplicación ρ : G → GL(n, K), g 7→ (ρij (g)) determina un
homomorfismo de grupos, ya que f g1 g2 = (f g1 )g2 . Entonces la acción de G en W está dada por
(
n
X
i=1
λi fi )g =
n X
n
X
λi ρij (g)fj .
i=1 j=1
Lo que falta probar es que ρ es un morfismo de variedades algebraicas. Notemos primero que, como f1 , ..., fn
son linealmente independientes, entonces, existen puntos x1 , ..., xn ∈ X, tales que det(fj (xk )) 6= 0. Ası́ que
la ecuación (3) puede ser resuelta mediante (fi (gxk )) = (ρij (g))(fj (xk )), o, de modo equivalente,
(ρi1 (g), ..., ρin (g)) = (fi (gx1 ), ..., fi (gxn ))A−1 ,
donde A = (fj (xk )). Ası́ que ρij es una función regular en G.
Ahora probaremos la segunda parte del lema. Sea {f1 , ..., fn } una base de W . Será suficiente probar que
el subespacio W1 generado por {fig : 1 ≤ i ≤ n, g ∈ G} es de dimensión finita.
Para esto definimos Fi ∈ A(G × X) como Fi (g, x) = fi (gx).
PComo A(G × X) = A(G) ⊗ A(X), entonces
podemos escribir Fi como una suma finita de la forma Fi =
Gij ⊗ Hij , con Gij ∈ A(G) y Hij ∈ A(X).
Sea W2 el subespacio generado por {Hij }. Como
X
fig (x) = Fi (g, x) =
Gij (g)Hij (x),
se sigue que W1 ⊂ W2 . Pero W2 es de dimensión finita, ası́ que W1 es de dimensión finita.
Lema 8. Sea G un grupo reductivo actuando en una variedad afı́n X y sean W1 y W2 subconjuntos de X,
G-invariantes, cerrados y disjuntos. Entonces existe f ∈ A(X)G tal que f (W1 ) = 0, f (W2 ) = 1.
Demostración. Sea h ∈ A(X) tal que h(W1 ) = 0 y h(W2 ) = 1. Por el lema (4) el subespacio vectorial de
A(X) generado por {hg : g ∈ G} es de dimensión finita. Si {h1 , ..., hn } es una base de este espacio, entonces
podemos escribir
X
hgi =
αij (g)hj ,
donde g 7→ (αij (g)) es un morfismo de G al grupo general lineal. Este morfismo determina una acción lineal
de G en K n y el morfismo
ψ : X → Kn
x 7→ (h1 (x), ..., hn (x))
20
es G-invariante, es decir, el diagrama
/X
G×X
IG ×ψ
G × Kn
ψ
/ K n,
conmuta.
Como < hg : g ∈ G >=< h1 , ..., hn >, entonces para todo x ∈ W1 y g ∈ G, hg (x) = h(gx) = 0, ası́ que
hi (x) = 0 para todo i, por tanto ψ(x) = (h1 (x), ..., hn (x)) = 0, es decir, ψ(W1 ) = 0. Sean x, y ∈ W2 y g ∈ G,
tenemos que hg (x) = hg (y) = 1, entonces hi (x) = hi (y) para todo i, por tanto ψ(W2 ) es un punto invariante
v ∈ K n , con v 6= 0.
Gracias a que G es geométricamente reductivo tenemos que existe f1 ∈ K[x1 , ..., xn ]G tal que f1 (0) = 0
y f1 (v) = 1. Entonces f = f1 ◦ ψ ∈ A(X)G y tiene las propiedades requeridas.
Ahora podemos probar el Teorema.
Demostración. Por el lema la acción de G en A(X) es racional, ası́ que por el Teorema de Nagata, A(X)G
es una K-álgebra finitamente generada. Probaremos que el par (Y, φ) definido anteriormente satisface las
condiciones del Teorema, es decir, es un cociente bueno:
1. Supongamos que existe g ∈ G y x ∈ X tales que φ(gx) 6= φ(x). Entonces, como Y es afı́n, existe
f ∈ A(Y ) tal que
f (φ(gx)) 6= f (φ(x))
es decir
φ∗ (f (gx)) 6= φ∗ (f (x)).
Esto contradice el hecho de que φ∗ (f ) ∈ A(X)G .
2. Sea y ∈ Y yPsean f1 , ..., fr generadores del ideal maximal en A(Y ) que corresponde
a y. Se sigue del
P
lema 6 que
fi R 6= R; ası́ que existe un ideal maximal de R que contiene a
fi R. Si x es el punto
de X correspondiente a este ideal maximal, entonces fi (x) = 0 para todo i, entonces φ(x) = y.
3. Como lo vimos en la demostración de la existencia del cociente bueno para acciones de grupos finito, es
suficiente probar el isomorfismo para los abiertos de la forma U = Yf para algún f ∈ A(Y ) = A(X)G .
En este caso tenemos que φ−1 (U ) = Xf , entonces, puesto que A(Yf ) = A(Y )f = (A(X)G )f , tenemos
que probar que (A(X)G )f = (A(X)f )G , para todo f ∈ A(X)G . Lo cual es claro.
4. Sean W1 y W2 subconjuntos de X invariantes, cerrados y disjuntos, entonces existe, por el lema 8,
f ∈ A(X)G tal que f (W1 ) = 0 y f (W2 ) = 1. Considerando f como elemento en A(Y ) tenemos que
f (φ(W1 )) = 0,
f (φ(W2 )) = 1;
ası́ que φ(W1 ) ⊂ f −1 (0), y φ(W2 ) ⊂ f −1 (1), por lo tanto φ(W1 ) ∩ φ(W2 ) = ∅.
5. Sea W ⊂ X invariante y cerrado. Supongamos que existe y ∈ φ(W ) − φ(W ). Aplicando el resultado
anterior a los cerrados W1 = W y W2 = φ−1 (y) concluimos que φ(W ) ∩ {y} = ∅, lo cual es una
contradicción.
Terminaremos esta sección con el siguiente ejemplo sencillo de cociente bueno.
21
Ejemplo 13. Recordar el ejemplo 2 donde tenemos la acción natural:
GL(n, K) × A(K)n → A(K)n
(g, (x1 , ..., xn )) 7→ g(x1 , ..., xn ),
el conjunto de órbitas consta de dos elementos, A(K)n /GL(n, K) = {A(K)n − {0}, {0}}, la órbita {0}
se acumula en A(K)n − {0} . Es fácil ver que los únicos polinomios invariantes por esta acción son los
constantes, es decir, A(A(K)n )GL(n,K) = K y, por tanto, la variedad Y del Teorema anterior es un punto y
el morfismo φ es constante, esto significa que en el cociente bueno estamos identificando las dos órbitas.
4.1.
Conjugación de Matrices
En esta subsección vamos a describir con detalle el ejemplo de la acción por conjugación del grupo general
lineal en el espacio de matrices, este ejemplo ilustra perfectamente lo que sucede geométricamente con las
órbitas en el cociente.
Sea X el conjunto de matrices cuadradas de tamaño n con coeficientes en C. Este conjunto es la variedad
2
afı́n A(C)n y en ella tenemos la acción por conjugación:
GL(n, C) × X → X
(G, A) 7→ GAG−1 ,
la cual es lineal. Sea A ∈ X, entonces O(A) = {GAG−1 : G ∈ GL(n, C)} y Est(A)
Pn = {G ∈ GL(n, C) :
GAG−1 = A}; consideremos su polinomio caracterı́stico χA (t) = det(tI −A) = tn + j=1 (−1)i cj (A)tn−j . Los
coeficientes del polinomio caracterı́stico son funciones cj : X → C continuas invariantes por la acción, pues el
polinomio caracterı́stico es invariante ante conjugación, ası́ que cj ∈ A(X)GL(n,C) = C[x1 , x2 , ..., xn2 ]GL(n,C)
y de hecho se tiene que estas funciones generan al álgebra de invariantes, es decir:
C[x1 , x2 , ..., xn2 ]GL(n,C) = C[c1 , ..., cn ],
estos generadores son algebraicamente independientes, esto significa que
J = {h ∈ C[x1 , ..., xn ] : h(c1 , ..., cn ) ≡ 0 en C[x1 , ..., xn ]} = {0}.
Entonces el Teorema de existencia de cocientes en variedades afines nos dice que (Cn , φ) es el cociente bueno
de la acción, donde
φ : X → A(C)n = Cn
A 7→ (c1 (A), ..., cn (A)).
La aplicación φ es invariante pues las funciones ci : X → C lo son, recordar que cn−1 (A) = traza A y
cn (A) = det A.
También sabemos que φ es sobre, en este caso podemos dar explı́citamente un elemento en la preimagen
de un punto en Cn . Para ello recordemos las siguientes definiciones: Una matriz A ∈ X es un endomorfismo
cı́clico de Cn si existe v ∈ Cn tal que {v, Av, ..., An−1 v} es base de Cn , y que cualquier vector con esta
propiedad se llama vector cı́clico para A.
Si v es un vector cı́clico para A y si An v = c1 An−1 v − c2 An−2 v + ... + (−1)n−1 cn v, entonces la matriz A
en la base {v, Av, ..., An−1 v} es:
22

A(c1 ,...,cn )
0
 1


=
 0
 .
 ..
0
1 , ..., cn ) ∈ C
PnDado (c
j
n−j
(−1)
c
.
jt
j=1
n
0
0
..
.
···
···
..
.
..
..
.
...
.
0
(−1)n−1 cn
(−1)n−2 cn−1
..
.
..
0
.
1
c1
0
0
..
.




.



(4)
tenemos que la matriz A(c1 ,...,cn ) tiene como polinomio caracterı́stico a tn +
Este ejemplo es sumamente interesante ya que en él podemos estudiar cuidadosamente la geometrı́a de
las órbitas que se acumulan en otras órbitas, este comportamiento de órbitas se repite en el caso general de
acciones en variedades afines.
Si φ(A) = φ(B), entonces no necesariamente O(A) = O(B). Por ejemplo las matrices



a 1
a



a
a






b
b



..
..
.
.
no son conjugadas entre sı́, es decir, O(A) 6= O(B), sin embargo A y B tienen el mismo polinomio caracterı́stico.
Sea A = As + An la descomposición de Jordan de la matriz A, es decir, As es la parte diagonalizable y
An la parte nilpotente, debido a que los valores propios están en la matriz As , tenemos que φ(A) = φ(As ).
Sea a ∈ C∗ y consideremos la matriz diagonal D = (1, a, ..., an−1 ). Se tiene entonces que:
D−1 As D = As
D−1 An D = aAn ,
ası́ que D−1 AD = As + aAn =: Aa . Entonces para todo a ∈ C∗ , Aa ∈ O(A) y, por tanto, A0 = As ∈ O(A).
Si φ(A) = φ(B), entonces φ(As ) = φ(Bs ), ası́ que existe G ∈ GL(n, C) tal que
As = GBs G−1
y As ∈ O(A) ∩ O(B).
Inversamente, si C ∈ O(A), tenemos, por la continuidad del polinomio caracterı́stico, que φ(C) = φ(A) y,
por tanto O(A) ∩ O(B) 6= ∅ implica que φ(A) = φ(B).
Hemos probado la siguiente proposición.
Proposición 2. Sean A, B ∈ X. Entonces, las siguientes afirmaciones son equivalentes:
1. O(A) ∩ O(B) 6= ∅,
2. φ(A) = φ(B),
3. A y B tienen los mismos valores propios.
En general tenemos que la dimensión de una órbita es la dimensión del grupo menos la dimensión del
estabilizador del punto, ası́ que en este caso dim O(A) = dim GL(n, C) − dim Est(A) = n2 − dim Est(A).
La dimensión máxima que podemos tener para una órbita es n2 − n, y se alcanza si los bloques de Jordan de la matriz A son de tamaño máximo para todo valor propio. Por ejemplo, la órbita de la matriz
23
A = (λ1 , λ2 , ..., λn ), donde λi 6= λj para i 6= j tiene dimensión n2 − n.
Para continuar con el estudio de la geometrı́a de la órbitas de esta acción es necesario caracterizar a las
matrices con órbitas cerradas.
Corolario 1. La órbita O(A) es cerrada en X si y sólo si A es diagonalizable.
Demostración. Sea A = An + As la descomposición de Jordan de A. Si O(A) es cerrada en X entonces,
As ∈ O(A) y por tanto A = As . Sólo resta probar que O(As ) es cerrada en X. Sea B ∈ O(As ) − O(As ),
entonces O(B) ⊂ O(As ) − O(As ), como B y As tienen los mismos valores propios entonces B tiene parte
nilpotente, ası́ que dim O(B) > dim O(As ) lo cual es una contradicción.
Ası́ que la órbita de una matriz A no es cerrada en X si y sólo si A tiene parte nilpotente en su descomposición de Jordan, y en O(As ) − O(As ) tendremos las órbitas de las matrices que tienen los mismos valores
propios
de Jordan
en laórbita
 de A pero
 con algún bloque

 de tamanño estrictamente menor. Por ejemplo

a 1 0
a 1 0
a 0 0
de  0 a 1  se acumula  0 a 0  y en la órbita de esta matriz se acumula  0 a 0  cuya
0 0 a
0 0 a
0 0 a
órbita es cerrada.
Concluimos que las matrices con órbitas cerradas que no van a estar en la cerradura de ninguna otra
órbita son las matrices con n valores propios distintos. Es decir, las matrices diagonalizables tal que la
dimensión de su órbita es maximal. Sea
X 0 = {A ∈ X : dim O(A) alcanza su valor máximo y O(A) es cerrada}
= {A ∈ X : A tiene n valores propios distintos}
este es un conjunto abierto en X, ya que es el conjunto de matrices cuyo polinomio caracterı́stico tiene n
raices distintas, es decir, es el conjunto de matrices en el que el discriminante del polinomio caracterı́stico es
distinto de cero. Consideremos la restricción del cociente bueno a este abierto:
φ|X 0 : X 0 → φ(X 0 )
A 7→ (c1 (A), ..., cn (A)),
es claro que la imagen inversa de todo punto (c1 , ...,P
cn ) ∈ φ(X 0 ) es una única órbita, de hecho es la órbita de
n
n
la matriz diagonal con las n raices distintas de t + j=1 (−1)j cj tn−j . Ası́ que esta restricción es un cociente
geométrico.
Por ejemplo, en el caso de matrices de tamaño 2 el cociente bueno está dado por φ : X → C2 , A 7→
(traza(A), det(A)) y los distintos bloques de Jordan son los siguientes:
a 1
a 0
a 0
A1 =
,
A2 =
,
A3 =
0 a
0 a
0 b
α β
donde a 6= b. Tenemos que Est(A1 ) = {
: α ∈ C∗ , β ∈ C}, ası́ que dim O(A1 ) = 2, O(A2 ) = {A2 },
0 α
α 0
Est(A3 ) = {
: α, β ∈ C∗ }, ası́ que dim O(A3 ) = 2. La órbita de A2 , que es cerrada, se acumula
0 β
en la órbita de A1 ; la órbita de A3 es cerrada y no se acumula en ninguna otra. El cociente geométrico se
obtiene considerando las matrices cuya descomposición de Zariski es de la forma A3 .
24
5.
Cocientes de Variedades Proyectivas
Como hemos dicho anteriormente, en general no es posible construir un cociente bueno de una acción
lineal de un grupo algebraico lineal G sobre una variedad proyectiva, X ⊂ Pn (K), sin embargo David Mumford demostró que, después de eliminar ciertos puntos de la variedad, sı́ existe un cociente bueno para la
acción.
Recordemos que, a diferencia del caso afı́n, los únicos morfismos algebraicos de una variedad proyectiva al
campo son las funciones constantes, ası́ que si G es un grupo reductivo actuando linealmente en la variedad
proyectiva X, consideraremos la acción inducida en el anillo de polinomios, es decir:
K[x0 , ..., xn ] × G → K[x0 , ..., xn ]
(f, g) 7→ f g (x0 , ..., xn ) = f (g(x0 , ..., xn )).
Los puntos que debemos eliminar para cosntruir el cociente bueno se llaman inestables, forman un cerrado
de Zariski de la variedad y son aquellos que se anulan en todos los polinomios invariantes, homogéneos no
constantes, los puntos en el complemente se llaman semiestables, aquı́ sı́ es posible constuir un cociente bueno
y, más aun, en este abierto tendremos un subconjunto, también abierto, con el que podremos construir un
cociente geométrico, como es de esperarse, estos puntos son aquellos cuya órbita es cerrada en el conjunto
de semiestables y con dimensión grande, estos puntos se llaman estables. Las definiciones precisas vienen a
continuación.
Definición 14. Decimos que x ∈ X es:
1. semiestable si existe f , polinomio invariante, homogéneo, de grado mayor o igual que uno tal que
f (x) 6= 0. Denotaremos el conjunto de puntos semiestables de X por X ss .
2. estable si es semiestable,
dim O(x) = dim G,
ss
y O(x) es cerrada en X . El conjunto de puntos estables de X lo denotaremos por X s .
3. Los puntos que no son semiestables se denominan puntos inestables.
El principal Teorema de la Teorı́a Geométrica de Invariantes, escrito en el contexto de variedades proyectivas, es el siguiente:
Teorema 9. (ver pag. 38 de [12]) Sea G un grupo reductivo actuando linealmente sobre una variedad
proyectiva X, entonces
1. Existe un cociente bueno (Y, φ) de X ss por G donde Y es proyectiva.
2. Existe Y s ⊂ Y abierto tal que φ−1 (Y s ) = X s y (Y s , φ) es un cociente geométrico de X s por G.
3. Si x1 , x2 ∈ X ss entonces
φ(x1 ) = φ(x2 ) ⇔ O(x1 ) ∩ O(x2 ) ∩ X ss 6= ∅.
Antes de dar el esbozo de la demostración de este importante Teorema observemos lo siguiente: Sea
R = {f ∈ K[x0 , ..., xn ] : f es homogéneo, invariante y no-constante}, entonces
[
X ss =
Xf ,
f ∈R
donde Xf = {x ∈ X : f (x) 6= 0}. Cada Xf es un abierto afı́n de X invariante por la acción de G. Por lo
tanto, usando el caso de acciones en variedades afines, sabemos que existe un cociente bueno (Yf , φf ) de Xf
25
por G. Mediante estos cocientes podemos construir una variedad Y cubierta por los abiertos afines Yf y un
morfismo φ : X ss → Y que define un buen cociente de X ss por G.
Debido a lo anterior, en la demostración del Teorema, necesitaremos la siguiente proposición, que exhibe
las propiedades locales de los cocientes bueno y geométrico.
Proposición 3. (ver [15]) Los conceptos de cociente bueno y cociente geométrico son locales respecto a Y ,
es decir,
1. si (Y, φ) es un cociente bueno (cociente geométrico) de X por G y U es un abierto de Y , entonces
(U, φ) es un cociente bueno (cociente geométrico) de φ−1 (U ) por G;
2. si φ : X → Y es un morfismo y {Ui } es una cubierta abierta de Y tal que (Ui , φ) es un cociente bueno
(cociente geométrico) de φ−1 (Ui ) por G para todo i, entonces (Y, φ) es un cociente bueno (cociente
geométrico) de X por G.
Demostración. (Teorema 9) Si X ⊂ P(K)n , entonces el cono afı́n de X es la variedad afı́n definida por
b = {x̄ ∈ A(K)n+1 : x̄ ∈ x ∈ X} ∪ {(0, ..., 0)}.
X
b → X,
b (g, x̄) 7→ gx̄, en el cono afı́n de X.
La acción de G en X induce una acción, G × X
1. Para demostrar esta parte usaremos los siguientes hechos generales sobre variedades proyectivas y Kálgebras graduadas: Para todo elemento f ∈ A(X̂) homogéneo, de grado positivo tenemos un abierto
afı́n Xf en X. Sea R una subálgebra de A(X̂) finitamente generada por elementos homogéneos y sea
XR =
[
Xf .
f ∈R
Entonces existen una variedad proyectiva Y y un morfismo φ : XR → Y tales que
a) Y está cubierta por conjuntos abiertos afines Yf , uno por cada elemento homogéneo de R de grado
positivo y A(Yf ) es isomorfo a (Rf )0 := {h ∈ Rf : h tiene grado cero};
b) φ−1 (Yf ) = Xf y φ : Xf → Yf es el morfismo correspondiente a la inclusión de (Rf )0 en (A(X̂)f )0 .
La acción de G inducida en A(X̂) preserva el grado de cada elemento homogéneo. Ası́ que R = A(X̂)G
es una subálgebra homogénea de A(X̂) y, por el Teorema de Nagata, es finitamente generada. Notemos
que XR = X ss y sea (Y, φ) el par que nos da la observación anterior.
Por el Teorema de Existencia de Cocientes en Variedades Afines, (b) y
((A(X̂)G )f )0 = ((A(X̂)f )0 )G ,
se sigue que (Yf , φ) es un cociente bueno de φ−1 (Yf ) = Xf por G, para cada elemento homogéneo
f ∈ RG de grado positivo. Y por la proposición 3 tenemos que (Y, φ) es un cociente bueno de X ss por
G.
2. Sea Y s = φ(X s ) y sea Y 0 la unión de abiertos Yf para los cuales la acción de G en Xf es cerrada,
es decir, las órbitas son cerradas en Xf . Claramente X s ⊂ φ−1 (Y 0 ) y entonces Y s ⊂ Y 0 . Por la
proposición 3 y por la parte (3) de la proposición 1 tenemos que (Y 0 , φ) es un cociente geométrico de
X 0 = φ−1 (Y 0). Se sigue que X s = φ−1 (Y s ) y que
Y 0 − Y s = φ(X 0 − X s ).
26
Ası́ que Y 0 − Y s es cerrado en Y 0 por la condición (iv) de cociente bueno, y Y s es abierto en Y 0 y,
por lo tanto, también es abieto en Y . Aplicando nuevamente la proposición 3 obtenemos que (Y s , φ)
es un cociente geométrico de X s .
3. Se sigue aplicando la segunda parte de la proposición 1.
5.1.
Ejemplos en Variedades Proyectivas
El grupo de automorfismos del espacio proyectivo complejo de dimensión n, P(C)n es isomorfo a la
proyectivización del grupo general lineal GL(n + 1, C), es decir, es isomorfo a P GL(n + 1, C) (ver ejemplo
7.1.1 de [6]). La aplicación SL(n + 1, C) → P GL(n + 1, C), g 7→ [g], que manda una matriz en su clase
de equivalencia, es una isogénia, esto significa que el núcleo es un conjunto finito, de hecho consta de las
matrices mútiplos de la identidad por una raı́z n + 1-ésima de la unidad; esto nos permite, en el contexto
de teorı́a de invariantes, trabajar indistintamente con cualquiera de ellos, lo haremos con el grupo especial
lineal SL(n + 1, C) que, como veremos, es más fácil de manejar.
1. Considerar la acción natural:
SL(n + 1, C) × CPn → CPn
(g, (x0 : ... : xn )) 7→ g(x0 : ... : xn ).
Que un polinomio f ∈ C[x0 , ..., xn ] sea invariante para la acción significa que f (g(x0 , ..., xn )) =
f ((x0 , ..., xn )) para todo g ∈ SL(n, C), pero esto sucede sólo si f es constante. Ası́ que en este caso tenemos que (CPn )ss = ∅.
2. En este ejemplo vamos a considerar la proyectivización del espacio de matrices cuadradas de tamaño
n con coeficientes en C y la acción por conjugación de SL(n, C), estaremos haciendo referencia al caso
afı́n que vimos con detalles en una sección precedente.
Sea X la proyectivización del espacio de matrices cuadradas de tamaño n con coeficientes en C y
consideremos la acción:
SL(n, C) × X → X
(G, A) 7→ GAG−1 .
Como vimos antes, todo polinomio invariante es un polinomio en los coeficientes del polinomio caracterı́stico, los cuales son homogéneos. Ası́ que una matriz A es inestable si y sólo si se anula en todos
los coeficientes del polinomio caracterı́stico, es decir, si su polinomio caracterı́stico es tn . Ası́ que la
matriz A es inestable si y sólo si todos sus valores propios son cero, como hemos excluido la matriz
cero para construir la proyectivización, entonces las matrices inestables serán aquellas cuya forma de
Jordan tiene ceros en la diagonal con al menos un bloque de Jordan de tamaño al menos 2.
Como en el caso afı́n la dimensión máxima de una órbita es n2 − n, si una matriz A fuera estable
entonces la dimensión de su órbita serı́a la dimensión del grupo que en este caso es n2 − 1, esto nos
está diciendo que para n > 1 no existen matrices estables, ası́ que en este caso el cociente geométrico
de la acción será vacı́o. Para construir el cociente bueno de esta acción daremos la siguiente definición.
27
Definición 15. Sean k1 , ..., kn ∈ N. Definimos el espacio proyectivo con pesos (k1 , ..., kn ) como
el conjunto de órbitas de la acción
C∗ × Cn − {(0, ..., 0)} → Cn − {(0, ..., 0)}
(l, (x1 , ..., xn )) 7→ (lk1 x1 , ..., lkn xn ).
A este espacio lo denotaremos por P(C)(k1 ,...,kn ) .
Si det(tI − A) = tn +
acción, donde
Pn
i=1 (−1)
i
ci (A)tn−i , entonces (P(C)(1,2,...,n) , φ) es el cociente bueno para la
φ : P(X)ss → P(C)(1,2,...,n)
A 7→ (c1 (A), ..., cn (A)).
El espacio proyectivo pesado aparece por la siguiente propiedad:
det(tI − A) = tn +
n
X
(−1)j cj (A)tn−j =⇒ det(tI − lA) = tn +
j=1
n
X
(−1)j lj cj (A)tn−j .
j=1
3. Sea C[x0 , x1 , ..., xn ]d = {f ∈ C[x0 , ..., xn ] : f es homogéneo
de grado d}. Entonces C[x0 , x1 , ..., xn ]d es
un espacio vectorial sobre C de dimensión N = n+d
,
y
un
elemento f es este espacio, define, salvo
d
múltiplo por un escalar no nulo, a la hipersuperficie V (f ) = {p ∈ P(C)n : f (p) = 0} en P(C)n . Con esto
hemos demostrado que la proyectivización de este espacio vectorial parametriza a las hipersuperficies
de grado d en P(C)n , denotaremos este espacio por Hipd (n) el cual es isomorfo a CPN −1 .
Sea G = SL(n + 1, C), consideramos la siguiente acción de G en Hipd (n):
G × Hipd (n) → Hipd (n)
(g, f (x0 , ..., xn )) 7→ (gf )(x0 , ..., xn ) := f (g −1 (x0 , ..., xn )).
El objetivo de este ejemplo es demostrar que toda hipersuperficie no singular es semiestable. Recordar
que una hipersuperficie V (F ) ∈ Hipd (n) tiene una singularidad en el punto p ∈ CPn si y sólo si:
f (p) = 0,
∂f
(p) = 0
∂xi
∀i = 0, ..., n.
Diremos que la hipersuperficie definida por f es no singular si no tiene puntos singulares. Notemos
que, por la fórmula de Euler:
df =
n
X
i=0
xi
∂f
,
∂xi
la primera ecuación puede ser eliminada. Si f es un elemento genérico en Hipd (n) y ∆ es el resultante
∂f
de los polinomios ∂x
(ver [20]); entonces ∆ es un polinomio homogéneo de grado (n + 1)(d − 1)n en los
i
coeficientes de f , es decir, podemos ver a ∆ como elemento de C[y0 , ..., yN ]. El polinomio ∆ se llama
∂f
el discriminante de Hipd (n) y su valor en f es cero si y sólo si los polinomios ∂x
tienen un cero
i
n
común en CP .
28
La variedad definida por ∆, es decir, V (∆) = {F ∈ Hipd (n) : ∆(F ) = 0} ⊂ Hipd (n), parametriza las
hipersuperficies en P(C)n de grado d que son singulares. En C[y0 , ..., yN ] tenemos la acción inducida
de SL(n + 1, C):
C[y0 , ..., yN ] × G → C[y0 , ..., yN ]
(φ, g) 7→ φg : CN +1 → C
f 7→ φ(gf ),
y como f es singular en p si y sólo si gf es singular en g(p) entonces ∆ resulta ser un polinomio
invariante por esta acción. Dado que ∆ se anula en el conjunto de hipersuperficies singulares en P(C)n
de grado d, entonces hemos probado el siguiente:
Teorema 10. Toda hipersuperficie no singular es un punto semiestable para la acción de SL(n + 1, C)
en Hipd (n).
4. Una forma binaria de grado d es un polinomio homogéneo fd = a0 xd + a1 xd−1 y + ... + ad−1 xy d−1 +
ad y d ∈ C[x, y]. Ası́ que, la proyectivización del espacio vectorial de formas binarias de grado d es
Hipd (1), y la hipersuperficie que define fd , es V (fd ) = {(α : β) ∈ P(C)1 : fd (α, β) = 0} el cual es un
conjunto de d puntos (contando multiplicidad) en P(C)1 . Como en el caso general, tenemos definida la
siguiente acción lineal:
SL(2, C) × Hipd (1) → Hipd (1)
(g, f (x, y)) 7→ f (g −1 (x, y)).
Analizaremos el primer caso no trivial que corresponde a d = 3. En este caso el discriminante es el
polinomio:
∆(a0 , a1 , a2 , a3 ) = 27a20 a23 − a21 a22 − 18a0 a1 a2 a3 + 4a0 a32 + 4a31 a3 ,
el cual satisface ∆ = 0 si y sólo si la forma binaria a0 x3 + a1 x2 y + a2 xy 2 + a3 y 3 tiene una raı́z repetida.
Además ∆(Y0 , Y1 , Y2 , Y3 ) ∈ C[Y0 , Y1 , Y2 , Y3 ] es homogéneo de grado 4 e invariante por la acción, ası́ que,
como ya habı́amos visto en el ejemplo anterior:
Hip3 (1)∆ = {a0 x3 + a1 x2 y + a2 xy 2 + a3 y 3 ∈ Hip3 (1) : ∆(a0 , a1 , a2 , a3 ) 6= 0} ⊂ Hip3 (1)ss .
Como sabemos, dados x1 , x2 , x3 , y1 , y2 , y3 ∈ P(C)1 tales que xi 6= xj y yi 6= yj si i 6= j, existe un único
elemento g ∈ SL(2, C) tal que g(xi ) = yi para i = 1, 2, 3. Es decir, dadas dos formas binarias f1 , f2
de grado 3 con tres raı́ces distintas cada una de ellas, existe g ∈ SL(2, C) tal que gf1 = f2 . Ası́ que
Hip3 (1)∆ consta de una única órbita.
Como Hip3 (1)∆ es un abierto de Hip3 (1)(' P(C)3 ), entonces dim Hip3 (1)∆ = 3 = dim SL(2, C). En
[8] podemos ver que todos los polinomios invariantes homogéneos, no constantes son de la forma k∆r
para algún k ∈ C, y un entero positivo r. Entonces Hip3 (1)∆ = Hip3 (1)ss , y esto implica también que
Hip3 (1)∆ = Hip3 (1)ss = Hip3 (1)s . Concluimos que los puntos inestables corresponden a las formas
binarias de grado 3 con al menos dos raices repetidas y que el cociente bueno es un punto.
29
6.
Criterio de Hilbert-Mumford
En esta sección describiremos un criterio que nos permite encontrar los puntos inestables y estables de
una acción lineal dada, este criterio hace uso de los subgrupos a 1-parámetro del grupo y se debe basicamente a los trabajos de David Hilbert y de David Mumford, es por esto que se conoce como el criterio de
Hilbert-Mumford.
Consideremos la acción lineal de un grupo reductivo G en una variedad proyectiva: G × X → X, (g, x) 7→
b el cono afı́n de X. Empezaremos con la siguiente proposición, la cual caracteriza los puntos
gx y sea X
semiestables y estables de acuerdo al comportamiento de la órbita del punto en el cono afı́n de la variedad.
b en la clase de x, entonces:
Proposición 4. (ver Proposición 2.2 de [12]) Sea x ∈ X y sea x̄ ∈ X
1. x es semiestable si y sólo si 0 ∈
/ O(x̄).
2. x es estable si y sólo si 0 ∈
/ O(x̄) , la órbita de x es cerrada en X ss y dim O(x) = dim G.
b en la clase de x.
Demostración. Sea x ∈ X y sea x̄ ∈ X
1. Supongamos que el punto x ∈ X es semiestable y sea f un polinomio, invariante, homogéneo de grado
positivo tal que f (x) 6= 0. Entonces f (x̄) 6= 0 y, por tanto, para todo y ∈ O(x̄), f (y) es una constante
no cero. Ası́ que 0 ∈
/ O(x̄).
Supongamos que 0 ∈
/ O(x̄). Por el lema 8 existe un polinomio invariante f tal que f (0) = 0 y f (O(x̄)) =
1. Si f = fm + fm+1 + ... + fd donde fj es homogéneo de grado j, entonces m > 0 y existe i tal que
fi (x̄) 6= 0. Entonces x es semiestable.
2. Esta parte es clara a partir de la definición de punto estable que dimos en la sección anterior.
Definición 16. Un subgrupo a un parámetro de G es un homomorfismo no trivial
λ : K∗ → G
de grupos algebraicos.
Si λ es un subgrupo a 1-parámetro de G y si G actúa linealmente en una variedad X, entonces λ define
una representación de K ∗ en K n+1 :
C∗ → GL(n + 1, K)
t 7→ λ(t) : K n+1 → K n+1
v 7→ λ(t)v,
donde, para simplificar la notación, consideramos λ(t) como elemento de GL(n + 1, K).
Proposición 5. La representación anterior es diagonalizable, es decir, existe {v0 , ..., vn } base de K n+1 tal
que λ(t)vi = tri vi , donde ri ∈ Z.
Demostración. Dado que K ∗ es un grupo conmutativo, entonces {λ(t)}t∈K ∗ es una familia conmutativa
m
de endomorfismos de K n+1 . Sea t0 ∈ K ∗ una raı́z m − ésima de la unidad, L
entonces
L λ(t0 ) es la matriz
n+1
identidad, por lo tanto λ(t0 ) es diagonalizable. Sea K
= ker(λ(t0 ) − a1 I) ... ker(λ(t0 ) − an+1 I) la
descomposición en subespacios propios lineales invariantes que define la diagonalización de λ(t0 ).
30
Sea E ∈ {λ(t)}t∈K ∗ y sea j un entero positivo menor o igual que n + 1 y v ∈ ker(λ(t0 ) − aj I), entonces
(λ(t0 ) − aj I)Ev = Eλ(t0 )v − aj Ev = E(aj v) − aj Ev = 0,
por lo tanto el subgrupo unidimensional ker(λ(t0 ) − aj I) es invariante por E, entonces E es diagonalizable
con la misma base que λ(t0 ). Sea {v0 , ..., vn } la base que diagonaliza estos endomorfismos, puesto que K ∗ es
un grupo multiplicativo, entonces λ(t)vi = tri vi donde ri ∈ Z.
Pn
a que la acción de G es lineal tenemos lo siguiente, si x̄ =
i=0 ai vi , entonces λ(t)x̄ =
PnGracias
ri
i=0 t ai vi . Tomando esto en cuenta establecemos la siguiente definición.
Definición 17. Sea x ∈ X y λ un subgrupo a un parámetro de G, definimos la siguiente función:
µ(x, λ) := min{ri : ai 6= 0}.
(5)
Ahora mencionamos el siguiente Lema, cuya demostración es consecuencia inmediata de la definición de
la función µ.
b tal que x̄ ∈ x. Sea g ∈ G y λ un
Lema 9. (ver pag. 104 y 108 de [15]) Sea x ∈ X. Tomemos x̄ ∈ X
subgrupo a 1-parámetro de G, entonces:
1. µ(x, λ) < 0 si y sólo si lı́mt→0 λ(t)x̄ no existe
2. µ(x, λ) > 0 si y sólo si lı́mt→0 λ(t)x̄ = 0.
3. µ(gx, λ) = µ(x, g −1 λg)
b tal que x̄ ∈ x. Sean g ∈ G y λ un subgrupo a 1-parámetro de G, entonces:
Demostración. Sea x̄ ∈ X
Pri ri
1. µ(x, λ) ≥ 0 si y sólo si 0 6 ri para todo ai 6= 0 y esto sucede si y sólo si lı́mt→0 λ(t)x̄ = lı́mt→0 i=0
t ai vi
exite.
Pri ri
2. µ(x, λ) > 0 si y sólo si 0 < ri para todo ai 6= 0 y esto pasa si y sólo si lı́mt→0 λ(t)x̄ = lı́mt→0 i=0
t ai v i =
0
3. Supongamos que {gv0 , ..., gvn } es una base que diagonaliza a λ, es decir, λ(t)gvi = tri gvi , entonces g −1 λ(t)gvi = g −1 (λ(t)gvi ) = g −1 (tri gvi ) = tri vi . Esto significa que {v0 , ..., vn } es una base que
diagonaliza a g −1 λg. Entonces µ(gx, λ) = µ(x, g −1 λg).
Es claro que si existe un subgrupo a 1-parámetro λ tal que lı́mt→0 λ(t)x̄ = 0, entonces x es un punto
inestable, esto debido a que este lı́mite pertenece a O(x̄). El siguiente Teorema (cuya demostración no es
inmediata) es el recı́proco de la afirmación anterior.
Teorema 11. (ver Teorema 2.1 de [12]) Si 0 ∈ O(x̄) entonces existe un subgrupo a un parámetro:
λ : K∗ → G
tal que lı́mt→0 λ(t)x̄ = 0.
Ahora establecemos el criterio de Hilbert-Mumford.
Teorema 12. (ver Teorema 4.9 de [15])
Sea G un grupo reductivo actuando linealmente en una variedad proyectiva X, entonces x ∈ X es:
1. semiestable si, y sólo si, µ(x, λ) ≤ 0 para todo λ, subgrupo a un parámetro de G. (inestable si, y sólo
si, existe un subgrupo a 1-parámetro λ de G tal que µ(x, λ) > 0.)
31
2. estable si, y sólo si, µ(x, λ) < 0 para todo λ, subgrupo a un parámetro de G.
Una de las facilidades que tenemos al trabajar con el grupo SL(n, K) es que sus subrupos a un parámetro
son diagonalizables, es decir:
Proposición 6. (ver [15]) Los subgrupos a un parámetro de SL(n, K) son de la forma
λ : K ∗ → SL(n, K)
 r
t1

..
t 7→ g 
.

t rn
 −1
g ,
donde r1 ≥ ... ≥ rn , r1 + ... + rn = 0 y g ∈ SL(n, K).
De esta proposición y de la parte (3) de 9 podemos concluir la siguiente
Proposición 7. Si SL(n, K) actúa linealmente en una variedad proyectiva X, entonces x ∈ X es semiestable
(respectivamente estable) si y sólo si para todo subgrupo a un parámetro de la forma
λ : K ∗ → SL(n, K)
 r
t1

..
t 7→ 
.

trn


donde r1 ≥ ... ≥ rn , r1 + ... + rn = 0 y todo g ∈ SL(n, K) tenemos que µ(gx, λ) ≤ 0 (respectivamente < 0).
6.1.
Ejemplos que hacen uso del Criterio de Hilbert-Mumford
1. Recordemos la acción lineal de SL(2, C) en el espacio Hipd (1) de formas binarias de grado d:
SL(2, C) × Hipd (1) → Hipd (1), (g, fd (x, y)) 7→ fd (g −1 (x, y)). De acuerdo a la proposición 7 tenemos
que la forma fd es inestable (no-estable) si y sólo si existen,
λ : C∗ → SL(2, C),
t 7→
t
0
0
t−1
,
subgrupo 1-parámetro y g ∈ SL(2, C) tales que µ(fd , g −1 λg) = µ(fd (g −1 (x, y)), λ) > 0 ( respectivamente ≥ 0). Si
d
d
X
X
λ(t)fd (g −1 (x, y)) = λ(t)(
ai xd−i y i ) =
t−r(d−i)+ri ai xd−i y i ,
i=0
i=0
entonces µ(fd (g −1 (x, y)), λ) = min{−rd + 2ri : ai 6= 0}. Sea i0 = min{i : ai 6= 0}. Entonces µ = −rd +
2ri0 > 0 (respectivamente ≥ 0) si y sólo si i0 > d2 (respectivamente i0 ≥ d2 ). Ası́ que fd (g −1 (x, y)) =
Pd
d−i i
y es semiestable (respectivamente estable) si y sólo si
i=0 ai x
fd (g −1 (x, y)) =
d
X
d
ai xd−i y i = y [ 2 +1] (
i=[ d
2 +1]
(respectivamente fd (g −1 (x, y)) =
d
X
i=[ d
2]
32
d
X
d
ai xd−i y i−[ 2 +1] )
i=[ d
2 +1]
d
ai xd−i y i = y [ 2 ] (
d
X
i=[ d
2]
d
ai xd−i y i−[ 2 ] ));
1
esto nos esta diciendo que el punto (1 : 0) ∈ P(C) tiene multiplicidad mayor que d2 + 1 para la forma si
y sólo si es inestable y tiene multiplicidad mayor que d2 si y sólo si la forma es no-estable. Concluimos
la siguiente proposición.
Proposición 8. La forma binaria de grado fd , es inestable (respectivamente no-estable) si y sólo si
tiene un cero de multiplicidad mayor que d2 (respectivamente mayor o igual que d2 ).
2. Consideremos ahora la acción de G = SL(3, C) en el espacio de curvas cúbicas planas Hip3 (2): G ×
Hip3 (2) → Hip3 (2), (g, f (x0 , x1 , x2 ) 7→ f (g −1 (x0 , x1 , x2 )). Denotaremos una curva cúbica plana por
f (x0 , x1 , x2 ) =a00 x30 + a10 x20 x1 + a01 x20 x2 + a20 x0 x21 + a11 x0 x1 x2
+a02 x0 x22 + a30 x31 + a21 x21 x2 + a12 x1 x22 + a03 x32
X
xi1 xj2 .
=
aij x3−i−j
0
Dejaremos al lector verificar las siguiente propiedades:
a) (1 : 0 : 0) es singular si y sólo si a00 = a10 = a01 = 0.
b) (1 : 0 : 0) es un punto triple si y sólo si a00 = a10 = a01 = a20 = a11 = a02 = 0.
c) Si (1 : 0 : 0) es un punto doble, entonces las tangentes en este punto son las lı́neas definidas por
a20 x21 + a11 x1 x2 + a02 x22 = 0. Puede suceder que definan una tangente doble.
d ) Dado g ∈ G, x es un punto singular (doble, triple) de f si y sólo si gx es un punto singular (doble,
triple) de gf , además, g preserva lı́neas tangentes.
Usando estas propiedades demostraremos lo siguiente.
Proposición 9. Una curva cúbica plana es estable si y sólo si es no singular.
Demostración. Una curva cúbica plana no es estable si y sólo si es equivalente bajo G a una para la
cual µ(f, λ) ≥ 0, para algún subgrupo a un parámetro:
λ : C∗ → SL(3, C)
t 7→ diag(tr0 , tr1 , tr2 ),
donde r0 ≥ r1 ≥ r2 y r0 + r1 + r2 = 0, esto implica que −2 ≤
µ(f, λ) = min{(i + j − 3)r0 − ir1 − jr2 : aij 6= 0}.
r0
r2
≤ − 21 . Es fácil verificar que
Supongamos que f tiene un punto singular x, podemos suponer, sin pérdida de generalidad, que
x = (1 : 0 : 0), ası́ que a00 = a10 = a01 = 0. Si tomamos r0 = 2, r1 = r2 = −1, entonces µ(f, λ) ≥ 0 y,
por tanto, f no es estable.
Supongamos que µ(f, λ) ≥ 0 para algún λ diagonal de la forma anterior, vamos a probar que f tiene
un punto singular. Se verifica fácilmente que µ(f, λ) ≥ 0 si y sólo si a00 = a10 = 0.
Supongamos que a01 6= 0, entonces µ(f, λ) ≥ 0 y esto implica que −2r0 − r2 ≥ 0, esto pasa si y sólo si
r1 = r0 , r2 = −2r0 , podemos entonces suponer que r0 = r1 = 1 y r2 = −2. Para estos valores de los ri ,
tenemos que µ(f, λ) = min{3(j − 1) : aij 6= 0}.
Sea j0 = min{j : aij 6= 0}. Entonces j0 ≥ 1, es decir,
µ(f, λ) ≥ 0 ⇒ ai0 = 0 ∀i.
Esto implica que f = x2 f1 para alguna curva de grado 2, entonces f es singular en la intersección de
x2 y f1 .
33
3. Pinceles de cónicas: en este ejemplo vamos a introducir el concepto de pincel de curvas planas de grado
d, daremos a su conjunto estructura de variedad proyectiva y con la acción de cambio de coordenadas
caracterizaremos los pinceles inestables de grado 2 de acuerdo a su lugar base.
Definición 18. Sean A, B ∈ C[x, y, z]d , al conjunto L = {k1 A + k2 B|A 6= B, (k1 : k2 ) ∈ P(C)1 } se le
llama Pincel de curvas planas de grado d generado por A y B.
Debido a que podemos parametrizar a las curvas planas de grado d por P(C)((d+1)(d+2)/2)−1 , enviando
un polinomio a sus coeficientes, entonces podemos ver a L como la lı́nea en este espacio proyectivo que
pasa por A y B.
Definición 19. El lugar base del pincel L se define como
B(L) = V (A) ∩ V (B) = {p ∈ P(C)2 |k1 A(p) + k2 B(p) = 0
∀(k1 : k2 ) ∈ P(C)1 }.
El teorema de Bezout nos da entonces la siguiente:
Proposición 10. Sea L un pincel de grado d definido por polinomios sin componentes en común,
entonces el conjunto base tiene a lo más d2 puntos distintos.
Sea Gd el conjunto de pinceles de grado d, daremos a este conjunto estructura de variedad algebraica
mediante las coordenadas de Plücker. Para ello tomamos L ∈ Gd y A, B ∈ L dos puntos distintos en
L, entonces
A=
d
X
i j d−i−j
ai,j x y z
B=
i,j=0
d
X
bi,j xi y j z d−i−j ,
i,j=0
y con estos coeficiente construimos la matriz de 2 × (d + 1)(d + 2)/2:
a0,0
b0,0
a0,1
b0,1
···
···
a0,d
b0,d
···
···
ad,0
bd,0
y tomamos los siguientes determinantes de 2 × 2
ai,j ak,l
Mi,j,k,l = det
= ai,j bk,l − ak,l bi,j .
bi,j bk,l
Notemos que en total tenemos el siguiente
número de combinaciones al formar los menores de tamanño
(d + 1)(d + 2)/2
2 × 2: N =
por lo que tenemos esa cantidad de coeficientes Mi,j,k,l . Ahora
2
bien, podemos darle el orden lexicográfico a los coeficientes Mi,j,k,l y esto nos permitirá ver estos N
elementos como un elemento de P(C)N −1 .
Definición 20. Consideremos la siguiente función:
P : Gd → P(C)N −1
L 7→ P(L) = (Mi,j,k,l ).
A la imagen de un pincel L bajo esta función se le llama coordenadas de Plücker para L.
34
Teorema 13. (ver [9]) Las coordenadas Mi,j,k,l de L son, salvo multiplicación por un escalar no cero,
independientes de la elección de A y B. Mas aún, la aplicación:
P : Gd → P(C)N −1
L 7→ P(L) = (Mi,j,k,l )
es un encaje cerrado.
Corolario 2. P(Gd ) es una variedad proyectiva.
Ahora describiremos la acción lineal inducida de SL(3, C) en la variedad proyectiva P(Gd ): SL(3, C)
actúa en C[x, y, z], C[x, y, z] × SL(3, C) → C[x, y, z], (f (x, y, z), g) 7→ f (g(x, y, z)) = f g. Entonces
SL(3, C) actúa en Gd de la siguiente manera:
G × Gd → Gd
(g, {k1 A + k2 B}(k1 :k2 )∈P(C)1 ) 7→ {k1 Ag + k2 Bg}(k1 :k2 )∈P(C)1 ,
y, por consiguiente, este grupo actúa en P(Gd ). Para el caso de pinceles de cónicas, es decir, pinceles
de grado 2 podemos consultar en [1] la demostración del siguiente Teorema.
Teorema 14. Sea LA,B el pincel generado por las cónicas A y B sin componentes en común. Entonces,
P(LA,B ) es inestable si y sólo si B(LA,B ) contiene a lo más 3 puntos distintos.
Para el caso de pinceles de cúbicas existe un análisis detallado de pinceles inestables y estables que
también hace uso del método de subgrupos a un parámetro. Este análisis puede consultarse en [10].
Referencias
[1] Claudia R. Alcántara, Daniel Sánchez-Argáez: Inestabilidad de Pinceles de Cónicas Planas y su Lugar
Base. Aceptado para su publicación en Aportaciones Matemáticas de la SMM.
[2] Armand Borel: Linear Algebraic Group. Springer-Verlag, 1969.
[3] David Cox, John Little, Donal O’Shea: Ideals, varieties and algorithms. Springer-Verlag, 1996.
[4] John Fogarty: Invariant Theory. W. A. Benjamin, Inc., 1969.
[5] William J. Haboush: Reductive groups are geometrically reductive. Ann. of Math., (2), 102, 1975.
[6] Robin Hartshorne: Algebraic Geometry. Springer-Verlag, 1997.
[7] George R. Kempf: Instability in Invariant Theory. Annals of Mathematics 108 (1978) 299-316.
[8] Joseph P. S. Kung, Gian-Carlo Rota: The Invariant Theory of Binary Forms. Bulletin of the American
Mathematical Society 10, 1984.
[9] Gerge K. Laksov: The determinantal formula of Schubert calculus. ActaMath.132, 153-162, 1974.
[10] Rick Miranda: On the Stability of Pencils of Cubic Curves. American Journal of Mathematics, 1980.
[11] T. Miyata, Masayoshi Nagata: Note on semi-reductive groups. J. Math Kyoto Univ. 3, 1963/64.
[12] John Fogarty, Frances Kirwan, David Mumford: Geometric Invariant Theory. Springer-Verlag, 1994.
35
[13] Masayoshi Nagata: Invariants of a group in a affine ring. J. Math Kyoto Univ. 3, 1963/64.
[14] Masayoshi Nagata: On the 14th problem of Hilbert. Amer Journal of Math 81, 1959.
[15] Peter Newstead: Introduction to Moduli Problems and Orbit Spaces. Springer-Verlag, 1978.
[16] Emmy Noether: Der Endlichkeitssatz der Invarianten endlicher Grupen. Math. Annalen 77, 1994.
[17] Vladimir Popov: On Hilberts Theorem on Invariants. Dolk. Akad. Nauk SSSR 246, no. 3, 2008.
[18] Graciela Reyes: El problema 14 de Hilbert. Tesis de Licenciatura, Universidad de Guanajuato, 2008.
[19] Walter Ferrer Santos, Álvaro Rittatore: Actions and invariants of algebraic groups. CRC Press, 2005.
[20] B. Sturmfels: Introduction to Resultants. Proc. Sympos. Appl. Math., Vol. 53, pages 25-39, Amer. Math.
Soc, 1998.
[21] Hermann Weyl: The Classical Groups. Their Invariants and Representations. Princeton University
Press, Princeton, N. J. , 1939.
36