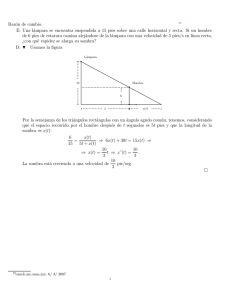
V E R SI´O N P R E LIM IN A R

IM
IN
AR
Capı́tulo 1
Preliminares
EL
En este capı́tulo incluimos prerrequisitos algebraicos y geométricos para
comprender el contenido del curso. Algunos temas se tratan con más profundidad que otros y daremos bibliografı́a para que el lector pueda completar
los temas que requiera.
PR
PARTE A: Geometrı́a Analı́tica
1.1
SIÓ
N
La geometrı́a analı́tica nace de la fusión de la geometrı́a clásica y del álgebra.
En este contexto el plano se describe mediante coordenadas, ası́ los objetos geométricos están dados por ecuaciones y los problemas geométricos se
convierten en problemas algebraicos.
Antes de comenzar el repaso de geometrı́a analı́tica propiamente dicha,
abordaremos el método de coordenadas.
Recta numérica
VE
R
La recta numérica es un objeto matemático que permite medir todos los
segmentos (una regla):
En una recta ilimitada se elige un punto O que se llama origen y una
unidad, es decir decimos que el segmento OU mide 1. También se incluye
una flecha que indica el sentido de crecimiento, como se indica en la figura
O
Figura 1.1
1
U
2
CAPÍTULO 1. PRELIMINARES
IM
IN
AR
Cuando ubicamos un punto A a la derecha del origen O y medimos el
segmento OA con respecto a la unidad elegida, identificamos el punto A con
la longitud del segmento OA y la escribimos a. Para un punto B que se
encuentra a la izquierda de O, asignamos un número negativo b. Es decir
que el segmento OB mide −b. De esta manera hemos asociado a cada punto
sobre la recta un número.
B
O
U
A
b
0
1
a
EL
Figura 1.2
Definición 1.1: Números reales
PR
Llamamos número real a todos los números que se obtienen de esta
manera.
SIÓ
N
A los puntos situados a la derecha de O se asignan números positivos, a los puntos situados a la izquierda de O se asignan números
negativos.
Observamos que en la recta hay dos puntos especiales:
•
•
O al que asignamos el número 0;
U al que asignamos el número 1.
VE
R
Dada una longitud ℓ, hay dos puntos A y A′ en la recta de manera que los
segmentos OA y OA′ tienen longitud ℓ : Ellos están situados simétricamente
con respecto al origen sobre la recta numérica. En la figura 1.3 hemos puesto
ejemplos de esta situación
B
A′
O
A
B′
−3
−1
0
1
3
Figura 1.3
3
1.1. RECTA NUMÉRICA
IM
IN
AR
Ejemplo 1.1
Si al punto P le corresponde el número 2 y ℓ = 3, encontrar los puntos X
sobre la recta para los cuales el segmento P X mide 3.
Solución ◮
Comenzamos analizando la situación en la figura 1.4
O
U
P
0
1
2
Figura 1.4
R
PR
EL
Hay dos puntos sobre la recta que cumplen con esta condición: uno a la
derecha de P y uno a la izquierda. Para obtener el punto a la derecha debemos movernos 3 unidades a la derecha, y de manera semejante, para obtener
el que está a la izquierda debemos movernos 3 unidades a la izquierda:
O
0
1
P
S
2
N
Figura 1.5
SIÓ
Las soluciones son los puntos R y S a los que corresponden,respectivamente,
los números −1 y 5.
◭
VE
R
En la recta numérica se interpretan las propiedades y las operaciones de
los números.
Ejemplo 1.2
Si al punto A le corresponde el número 2 y B está situado a la izquierda de
A, ¿qué número le corresponde a B si la longitud del segmento AB es 3?
Solución ◮
Podemos referirnos solamente a la figura 1.6: Ubicamos el punto A y después
contamos 3 unidades a la izquierda para localizar a B
Obtenemos que
4
CAPÍTULO 1. PRELIMINARES
B≡b 0
Figura 1.6
IM
IN
AR
A≡2
b = −1.
1.1.1
◭
Orden en la recta númerica
PR
EL
Cuando damos una orientación a la recta, en nuestro caso de izquierda a
derecha, representado por la flecha de crecimiento lo que queremos decir es
que cualquier número en la recta que se encuentra a la derecha de otro es
mayor que este. Veamos qué sucede cuando los puntos están a la derecha
del origen y A está a la derecha de B.
O
B
A
0
b
a
N
Figura 1.7
b < a.
VE
R
SIÓ
Por lo que dijimos anteriormente, a mide la longitud del segmento OA
mientras que b mide la longitud del segmento OB. Como el segmento OA es
más grande que el segmento OB tenemos que b es menos que a y escribimos
• A todo punto a la izquierda del origen le corresponde un número
negativo.
• Todo número negativo es menor que todo número positivo.
Cuando A está a la derecha de B y ambos a la izquierda del origen, la
situación es la siguiente,
5
1.1. RECTA NUMÉRICA
B
A
O
A′
B′
b
a
0
a′
b′
IM
IN
AR
Figura 1.8
entonces a′ = −a y b′ = −b y ahora B ′ está a la derecha de A′ . Por lo
tanto b < a equivale a que −a′ < −b′ .
Observemos que si A′ es el simétrico de A, con respecto al origen, igualmente se tiene que A es el simétrico de A′ con respecto al origen. Usando las
notaciones de la figura 1.7, tenemos que a′ = −a y a = −a′ es decir
a = −(a′ ) = −(−a).
EL
Propiedades del orden
PR
Con lo que hemos construido hasta el momento tenemos las siguientes propiedades
del orden;
• Todo número distinto de 0 o bien es positivo o bien es negativo;
• si a < b y b < c entonces a < c.
SIÓ
N
Más adelante veremos cómo se comporta el orden con respecto a las operaciones.
Para no tener que hacer cada vez la observación si A está a la derecha o a
la izquierda del origen para calcular la longitud del segmento OA definimos
VE
R
Definición 1.2: Valor absoluto
El valor absoluto de un número a se escribe |a| y se calcula mediante
la regla

 a si a > 0
|a| =
0 si a = 0

−a si a < 0
Por lo tanto el segmento que une A con O tiene longitud (o magnitud)
|a|. Denotamos por |OA| a la longitud del segmento OA. Observemos que
6
CAPÍTULO 1. PRELIMINARES
OA = AO
1.1.2
Suma geométrica de números reales
O
A
0
a
IM
IN
AR
Tomamos dos puntos sobre la recta numérica A y B con A a la izquierda
de B (es decir el número a es más chico que el número b) nos proponemos
definir a + b.
B
b
Figura 1.9
EL
Lo que hacemos es poner el segmento OA a continuación del segmento
OB ası́ obtenemos un segmento OC tal que
PR
|OC| = |OB| + |BC| = |OB| + |OA|.
A
B
C
0
a
b
a+b
Figura 1.10
SIÓ
N
O
VE
R
Cuando queremos sumar cualquier par de puntos debemos tener en cuenta
la orientación. Si A está a la izquierda de O entonces el número a que
corresponde a A es negativo (a < 0). El segmento OA es igual al segmento
AO como notamos antes. Pero si queremos decir que vamos de O hacia A
−→
escribimos OA.
Interpretamos lo que hicimos para la suma de la manera siguiente:
−→
−−→
Pusimos OA a continuación de OB.
Si A está a la izquierda de B y ambos a la izquierda de O, la situación se
ve en las figuras 1.10 y 1.11
7
1.1. RECTA NUMÉRICA
C
A
B
O
a
b
0
IM
IN
AR
Figura 1.11
−→
−−→
y hacemos lo mismo que antes, es decir ponemos OA a continuación de OB
ası́ obtenemos un punto C a la izquierda de A de manera que |CB| = |OA|
y
|OC| = |OB| + |BC| = |OB| + |OA|,
C
A
B
a+b
C
a
b
O
0
a+b
0
PR
b
O
EL
B
Figura 1.12
B
VE
R
b
SIÓ
Solución ◮
Comencemos con la figura 1.13
N
Ejemplo 1.3
Encontrar de manera geométrica la suma de −3 con 2.
O
0
Figura 1.13
A
a
−→
−−→
Ponemos OA a continuación de OB
B
−3
O
0
Figura 1.14
A
2
8
CAPÍTULO 1. PRELIMINARES
Por lo tanto, geométricamente hemos llegado a que
(−3) + 2 = −1
IM
IN
AR
Tomamos dos puntos sobre la recta numérica A y B con A a la izquierda
de B (es decir el número a es más chico que el número b) el segmento que une
a con b mide a − b sin importar dónde está situado el origen con respecto
a esos puntos.
b
a
Figura 1.15
PR
EL
El lector se puede entretener viendo esto ubicando el origen en todas las
posibles posiciones (hay 5).
Si a es más chico que b, es decir cuando a se localiza a la izquierda de
b, el segmento que los une mide b − a. Usando la definición 1.2, la longitud
del segmento que une los puntos a y b de la recta numérica es |a − b|.
Esto permite resolver el ejemplo 1.3 de manera puramente algebraica:
N
Tenemos que a = 2. Como el punto B se encuentra a la izquierda de A
entonces la longitud del segmento está dada por a−b. Obtenemos la ecuación
SIÓ
3 = a − b = 2 − b.
Al resolverla obtenemos que
VE
R
Ejercicios
b = 2 − 3 = −1.
Resuelva los siguientes ejercicios geométrica y algebraicamente.
1. Si al punto A le corresponde el número 1 y B está situado a la derecha
de A, ¿qué número le corresponde a B si la longitud del segmento AB
es 4?
2. Si al punto A le corresponde el número −1 y B está situado a la derecha
de A, ¿qué número le corresponde a B si la longitud del segmento AB
es 5?
9
1.1. RECTA NUMÉRICA
3. Si al punto A le corresponde el número −1 y B está situado a la
izquierda de A, ¿qué número le corresponde a B si la longitud del
segmento AB es 2?
IM
IN
AR
4. Si al punto A le corresponde el número −2 y B está situado a la derecha
de A, ¿qué número le corresponde a B si la longitud del segmento AB
es 2?
EL
En lo que sigue identificaremos el punto geométrico con el número
que asignamos. Esta es la versión geométrica de los números. Se dice
geométrica porque hemos asignado a cada punto de la recta, que es un
objeto geométrico, un número.
Vale la pena recordar las propiedades algebraicas de los números. Estas
propiedades aparecerán múltiples veces en lo que sigue:
Propiedades de la suma de números reales
PR
• La suma es conmutativa. Dados dos números reales a y b siempre
se tiene que
a+b=b+a
N
• La suma es asociativa. Dados tres números reales a, b y c siempre
se tiene que
(a + b) + c = a + (b + c).
SIÓ
Notemos que la suma se define entre dos números. La asociatividad
nos permite no tener que especificar cuáles de las posibles sumas se
hacen primero.
VE
R
• Existencia de elemento neutro para la suma. Dado un número
real a siempre se tiene que
a + 0 = 0 + a = a.
Notemos que 0 es la longitud de un “segmento” que se reduce a un
punto (es decir, un segmento que tiene el mismo extremo izquierdo y
extremo derecho).
• Existencia de un inverso aditivo. Dado un número real a existe
un único número real b que hace que
a + b = 0.
10
CAPÍTULO 1. PRELIMINARES
IM
IN
AR
Notemos que cuando tenemos un número real ubicado en la recta
numérica, el inverso aditivo es el número sobre la recta simétrico
con respecto al origen. El inverso aditivo de a se denota por −a
−a
0
b
0
a
−b
Figura 1.5
Propiedades del producto de números reales
EL
El producto entre número real fijo tiene que ver con la noción de proporcionalidad y para su interpretación gemétrica requerimos usar el plano
cartesiano y la abordaremos más adelante.
PR
• El producto es conmutativo. Dados dos números reales a y b
siempre se tiene que
ab = ba
N
• El producto es asociativo. Dados tres números reales a, b y c
siempre se tiene que
(ab)c = a(bc).
SIÓ
Al igual que la suma, el producto se define entre dos números y, de
nuevo, la asociatividad nos permite no tener que especificar cuáles de
los posibles productos se efectúan primero.
VE
R
• Existencia de elemento neutro para el producto. Dado un
número real a siempre se tiene que
a1 = 1a = a
• Existencia de un inverso multiplicativo. Dado un número real a
no nulo (esto se escribe: a 6= 0) existe un único número real b que
hace que
ab = 1.
El inverso aditivo de a se denota por
1
a
o bien a−1
11
1.1. RECTA NUMÉRICA
Propiedad que vincula la suma y el producto de números
• La suma distribuye con respecto al producto. Dados tres números
reales a, b y c siempre se tiene que
También
IM
IN
AR
(a + b)c = ac + bc.
a(b + c) = ab + ac.
Hacemos explı́cita esta última propiedad, aunque se puede derivar de
la primera, debido a la conmutatividad de la suma y del producto
Propiedades que relacionan el orden y las operaciones
a+b>0
EL
• Si a > 0 y b > 0 entonces
• Si a > 0 y b > 0 entonces
PR
• Si a < 0 y b < 0 entonces
ab > 0
ab > 0
N
Veamos que, a partir de estas propiedades, podemos concluir otras propiedades
de las operaciones de los números. Las deducciones que siguen tienen por
objetivo dar una idea de la manera como funciona un sistema deductivo.
SIÓ
Ejemplo 1.4
Para todo número real a,
VE
R
a0 = 0.
Solución ◮
Como 0 + 0 = 0 Entonces
a0 = a(0 + 0)
Por la distributividad del producto con respecto a la suma
a(0 + 0) = a0 + a0.
Por lo tanto
a0 = a(0 + 0)
= a0 + a0.
12
CAPÍTULO 1. PRELIMINARES
Sumamos a ambos lados de la igualdad el inverso aditivo de a0 y obtenemos
a0 + (−a0)
(a0 + a0) + (−a0)
a0 + (a0 + (−a0))
a0.
IM
IN
AR
0 =
=
=
=
Cuando juntamos las igualdades anteriores, obtenemos
0 = a0.
EL
Ejemplo 1.5
Si ab = 0 y a 6= 0 entonces b = 0.
◭
Solución ◮
Como a 6= 0, a tiene inverso multiplicativo. Entonces
PR
a−1 (ab) = a−1 (0)
(∗)
SIÓ
N
Por la asociatividad del producto a−1 (ab) = (a−1 a)b y por la propiedad que
define el inverso, (a−1 a)b = 1(b) = b. Hemos mostrado que el lado izquierdo
de (*) es igual a b. Ya vimos que el lado derecho es igual a 0. por lo tanto
b = 0.
◭
Propiedades de la función Valor Absoluto
• Si a = 0 entonces |a| = 0 y si |a| = 0 entonces a = 0.
VE
R
• Desigualdad del triángulo
|a + b| ≤ |a| + |b|.
Además
|a + b| = |a| + |b|
significa que a y b tienen el mismo signo.
• El valor absoluto se comporta de manera más simple con el producto:
|ab| = |a| |b|.
13
1.2. GEOMETRÍA ANALÍTICA PLANA
Otras propiedades de los números reales.
• Si a 6= 0 entonces a2 > 0.
• |a|2 = a2 .
1.2
Geometrı́a analı́tica plana
IM
IN
AR
• −a = (−1)a.
EL
El plano cartesiano es un plano en el cual hemos distinguido un punto,
llamado origen, y dos rectas numéricas ortogonales que se intersectan en el
origen. Con estos elementos es posible ubicar todos los puntos del plano
utilizando dos números. A cada punto le asignaremos dos números: la
abscisa y la ordenada como se muestra en la figura siguiente
y
A(2, 3)
PR
3
N
−1
SIÓ
O
VE
R
B(−1, −2)
2
x
−2
Figura 1.16
Las rectas numéricas se llaman ejes coordenados. Hemos marcado en
la figura 1.16 el eje horizontal con x. Esta recta se llama el eje de las x o
eje de las abscisas, mientras que la recta vertical está marcada con y y se la
conoce como eje de las y o de las ordenadas.
14
CAPÍTULO 1. PRELIMINARES
1.2.1
IM
IN
AR
Los puntos del plano se denotarán por letras mayúsculas A, B, . . . P, Q
y, para simplificar, las coordenadas de cada punto se denotaran por la letra
minúscula correspondiente con subı́ndice 1 para la primera coordenada y
subı́ndice 2 para la segunda. Ası́ escribiremos P (p1 , p2 ) que se lee “el punto P
tiene primera coordenada (o abscisa) p1 y segunda coordenada u (ordenada)
p2 .
Distancia entre dos puntos
Ahora queremos medir la distancia entre A y B. Tracemos en la figura 1.7
el segmento AB y tracemos CA y CB de manera que el triángulo ABC es
rectángulo en el vértice C y los catetos son paralelos a los ejes coordenados.
y
A(2, 3)
PR
EL
3
SIÓ
B(−1, −2)
VE
R
2
O
N
−1
−2
x
C(2, −2)
Figura 1.17
Por lo que vimos en la sección anterior, el segmento BC mide lo mismo
que el segmento que une −1 con 2 en el eje de las abscisas. Es decir,
|BC| = 2 − (−1) = 3
y el segmento AC, que mide lo mismo que el segmento que une 3 con −2 en
el eje de las ordenadas, mide
|AC| = 3 − (−2) = 5
15
1.2. GEOMETRÍA ANALÍTICA PLANA
Por el Teorema de Pitágoras, el cuadrado de la hipotenusa (que es el segmento AB) es igual a la suma de los cuadrados de los catetos. Por lo tanto
IM
IN
AR
|AB|2 = |AC|2 + |BC|2
|AB|2 = 32 + 52 = 34
y obtenemos que la longitud del √
segmento AB o, lo que es lo mismo la
distancia entre A y B es igual a 34.
En general, la distancia entre los puntos P (p1 , p2 ) y Q(q1 , q2 ) está dada
por
p
dist (P, Q) = (p1 − q1 )2 + (p2 − q2 )2 .
El primer término |p1 − q1 | mide la longitud del cateto paralelo al eje x y el
segundo |p2 − q2 | mide la longitud del cateto paralelo al eje y.
Rectas
EL
1.2.2
PR
Las rectas son uno de los objetos elementales de la geometrı́a euclidiana y,
uno de los principios de la geometrı́a euclidiana, es que dos puntos distintos
del plano determinan una recta. Desde el punto de vista de la geometrı́a
analı́tica es que una recta es el conjunto de todas las soluciones de una
ecuación, que se llamará lineal porque, en el caso del plano, determina una
lı́nea.
N
Ecuaciones cartesianas de las rectas en el plano
SIÓ
• Ecuación de una recta en el plano que no es paralela al eje de las y :
y = mx + b.
m se llama la pendiente.
VE
R
• Ecuación de una recta paralela al eje de las y :
x=c
• Ecuación general de una recta en el plano o ecuación normal:
ax + by = c
con a 6= 0 o b 6= 0 (una manera de escribir esto es a2 + b2 6= 0).
En la próxima sección veremos porqué se llama ası́. Para este tipo
de ecuaciones no hay que distinguir si las rectas son o no paralelas
16
CAPÍTULO 1. PRELIMINARES
IM
IN
AR
al eje de las y, puesto que la ecuación x = c que describe una recta
paralela al eje de las y es una ecuación normal. Notemos que si b 6= 0
entonces podemos conseguir de la ecuación normal, una ecuación de
tipo 1 despejando y
c
a
y =− x+ .
b
b
La pendiente de la recta es entonces
a
m=−
b
Rectas paralelas
Dos rectas en el plano que no se intersectan se dicen paralelas. Maneras
de reconocerlas a partir se sus ecuaciones
EL
• Dos rectas descritas por el primer tipo de ecuación y = m1 x + b1 y
y = m2 x + b2 son paralelas si
m1 = m2 .
PR
• Para decidir si las rectas a1 x + b1 y = c1 y a2 x + b2 y = c2 son paralelas
debemos comprobar primero que
a1 b2 = a2 b1
SIÓ
Ejemplo 1.6
Decidir si las rectas
N
y después debemos ver que hay un punto en una de ellas que no está
en la otra.
3x + 4y = 4,
y = −0.75x + 2
VE
R
son paralelas
Solución ◮
Estamos en la situación en que tenemos que las ecuaciones de las rectas no
son del mismo tipo. Como el coeficiente de y de la ecuación normal no se
anula, despejamos y obtenemos que
4y = −3x + 4
−3x + 4
y =
4
−3
+1
y =
4
17
1.2. GEOMETRÍA ANALÍTICA PLANA
La primera recta también tiene por ecuación y = −0.75x+1 que no intersecta
a la recta y = −0.75x + 2. por lo tanto las rectas son paralelas.
◭
Ejemplo 1.7
Tomemos a y b dos números reales no nulos.
IM
IN
AR
El siguiente ejemplo ilustra geométricamente la multiplicaión de números
reales.
Solución ◮
Consideremos la figura donde hemos ubicado a, b y las unidades.
b
1
1
a
−x
y=
+1
a
ab
x
SIÓ
N
O
−x
+b
a
PR
y=
EL
y
VE
R
Figura 1.18
La recta que une (a, 0) con (0, 1) tiene ecuación:
1
y = − x + 1.
a
Por lo tanto la recta paralela a esta recta que pasa por el punto (0, b) tiene
por ecuación
1
y = − x + b.
a
18
CAPÍTULO 1. PRELIMINARES
IM
IN
AR
Esta recta intersecta el eje de las x cuando y = 0, es decir cuando x es
solución de la ecuación
1
0=− x+b
a
o sea para
x = ab.
Esto funciona siempre aunque en la figura 1.18 hayamos puesto a y b
mayores que 1. Invitamos al lector a hacer lo mismo cuando a = b = −1.
◭
Rectas perpendiculares
PR
EL
En geometrı́a plana, una manera de reconocer si dos rectas que passan por
el origen son perpendiculares es comprobando que al ecoger un punto en
cada una de las rectas, el triángulo formado por estos puntos y el origen es
rectángulo. Tomemos dos rectas con ecuación de tipo 1 que pasan por el
origen. Veremos que hay una fómula algebraica que nos permite decidir si
son o no perpendiculares.
y = m1 x
y
P1
VE
R
SIÓ
N
P2
y = m2 x
O
x
Figura 1.19
Las ecuaciones de las rectas son y = m1 x y y = m2 x. Tomemos sobre
ellas dos puntos distintos del origen, es decir tomemos a 6= 0 y b 6= 0 y
P1 (a, m1 a), P2 (b, m2 b). Entonces, por el teorema de Pitágoras:
|OP1 |2 + |OP2 |2 = |P1 P2 |2 .
19
1.2. GEOMETRÍA ANALÍTICA PLANA
Por lo tanto
(a2 + (m1 a)2 ) + (b2 + (m2 b)2 ) = (a − b)2 + (m1 a − m2 b)2 .
IM
IN
AR
Reacomodamos y desarrollamos los binomios al cuadrado:
a2 + b2 + m21 a2 + m22 b2 = a2 − 2ab + b2 + m21 a2 − 2m1 m2 ab + m22 b2 ,
simplificamos
0 = −2ab − 2m1 m2 ab
o bien
2ab = −2m1 m2 ab.
EL
Como 2ab 6= 0 podemos volver a simplificar y obtenemos que las rectas son
perpendiculares si
1 = −m1 m2
PR
Las rectas perpendiculares a las rectas de ecuación x = c son aquellas que
tienen por ecuación y = d. Notemos que estas dos rectas se intersectan en
el punto P (c, d).
N
Las rectas perpendiculares a las rectas de ecuación y = d son aquellas que
tienen por ecuación x = c. Notemos que estas dos rectas también se intersectan en el punto P (c, d).
SIÓ
Para decidir si las rectas a1 x+ b1 y = c1 y a2 x+ b2 y = c2 son perpendiculares
debemos comprobar que
a1 b2 + a2 b1 = 0.
VE
R
Ejemplo 1.8
Mostrar que la recta que pasa por los puntos (5, −1) y (−5, −5) es perpendicular a la recta que pasa por los puntos (2, −2) y (0, 3).
Solución ◮
Para resolver el ejercicio debemos calcular las pendientes de las rectas. La
pendiente de la primera recta es:
m1 =
−4
2
−5 − (−1)
=
= .
−5 − (5)
−10
5
20
CAPÍTULO 1. PRELIMINARES
La pendiente de la segunda recta es
3 − (−2)
5
5
=
=− .
0 − (2)
−2
2
IM
IN
AR
m2 =
Como ninguna de las pendientes es igual a 0, las rectas son perpendiculares
cuando el producto de sus pendientes es igual a −1. En este caso
5
2
−
= −1.
m1 m2 =
5
2
1.2.3
Cı́rculos
◭
EL
Una circunferencia en el plano requiere de dos elementos para ser descrita:
un centro y un radio
PR
Definición 1.3
Una circunferencia de centro C y radio r está conformada por todos
los puntos que distan r de P.
N
Por lo tanto si el centro está dado por C(p, q) y el radio por r, la ecuación
de la circunferencia es
SIÓ
(x − p)2 + (y − q)2 = r 2
VE
R
Utilizando geometrı́a analı́tica podemos resolver ejercicios como en el
siguiente
Ejemplo 1.9
Considere el cı́rculo de radio 5 con centro en el origen y el punto P (3, 4) en
él. Muestre que la recta perpendicular a la recta que une el origen con P en
el punto P es tangente a la circunferencia.
Solución ◮
La ecuación de la circunferencia es
x2 + y 2 = 25.
21
1.2. GEOMETRÍA ANALÍTICA PLANA
Verifiquemos que el punto P está sobre la circunferencia. Para ello debemos
remplazar las coordenadas de P en la ecuación de la circunferencia:
P
EL
O
IM
IN
AR
x2 + y 2 = 32 + 42 = 9 + 16 = 25.
PR
Figura 1.20
La ecuación de la recta que pasa por el origen y por P tiene pendiente
4/3. Por lo tanto la ecuación de la recta es
4
x.
3
N
y=
VE
R
SIÓ
Por lo tanto la pendiente de la recta perpendicular a la recta anterior es
−3/4. La ecuación de la recta con pendiente −4/3 que pasa por el punto
P (3, 4) es
3
y − 4 = − (x − 3).
4
Podemos simplificar la ecuación anterior:
3
3
y = − x+3 +4
4
4
25
3
= − x+ .
4
4
Estudiemos la intersección de esta recta con la circunferencia. Como el
punto de intersección debe satisfacer ambas ecuaciones se debe tener que
x2 + y 2 = 25
22
CAPÍTULO 1. PRELIMINARES
y que
IM
IN
AR
3
25
y =− x+ .
4
4
Remplazamos este valor de y en la primera ecuación y obtenemos que para
que un punto esté en la intersección su abscisa debe satisfacer la ecuación
3
25 2
25 = x + y = x + − x +
.
4
4
2
2
2
EL
Desarrollando el binomio al cuadrado, agrupando y efectuando las operaciones
2
2
3
25
25
3
2
2
x −2
x+
25 = x + −
4
4
4
4
25
150
625
=
x2 −
x+
16
16
16
Multiplicamos ambos lados de la ecuación por 16/25
PR
16 = x2 − 6x + 25,
o bien
x2 − 6x + 9 = 0.
VE
R
SIÓ
N
Como x2 − 6x + 9 = (x − 3)2 , la ecuación tiene una única solución x = 3.
Finalmente remplazando en la ecuación de la recta obtenemos y = 4. Es
decir, el único punto en común entre la recta y la circunferencia es el punto
P. Por ello la recta
25
3
y =− x+
4
4
es tangente a la circunferencia.
◭
23
1.3. ÁNGULO ENTRE DOS RECTAS
PARTE B: Trigonometrı́a
Ángulo entre dos rectas
IM
IN
AR
1.3
ℓ1
A
ℓ2
D
O
B
EL
C
PR
Figura 1.21
SIÓ
N
Los ángulos entre dos rectas distintas ℓ1 y ℓ2 miden la “apertura” entre
ellas. Se obtienen cuatro ángulos:dos de ellos en color liso que se denotan
\ y BOC,
\ dos en color rayado que se denotan por AOB
\ y COD
\
por DOA
A pesar de que en cada caso partimos desde una semi-recta hacia otra
semi-recta, los ángulos entre dos rectas no son orientados, es decir, por
ejemplo
\ = AOD,
\
DOA
es decir, el ángulo es el mismo si vamos de ℓ1 hacia ℓ2 o de ℓ2 hacia ℓ1 .
VE
R
\ y BOC
\ se dicen opuestos por el vértice y son iguales,
Los ángulos DOA
\
también son opuestos por el vértice e iguales los ángulos \
AOB y COD.
[ COA,
[ BOD,
\ y DOB
\ se llaman ángulos llanos.
Los ángulos AOC,
\ y BOC
\ se dicen ángulos
Ası́ como está elaborada la figura, los ángulos DOA
\ se dicen ángulos obtusos.
agudos y los ángulos \
BOA y DOC
\ y AOB
\ comparten una semi-recta y el ángulo total
Como los ángulos DOA
\ es un ángulo llano, los ángulos se dicen
que se forma, es decir el ángulo BOA
ángulos suplementarios.
24
CAPÍTULO 1. PRELIMINARES
IM
IN
AR
Cuando tratemos con ángulos entre rectas, estos serán ángulos menores
o iguales a un ángulo llano.
En la figura 1.21 hemos colocado más puntos sobre las rectas y tenemos que
todas las expresiones siguientes se refieren al mismo ángulo
\
[,
AOB, AOT
\
BOA, T[
OA,
\ ROT
[,
ROB,
\ T[
BOR,
OR.
B
EL
T
R
A
PR
O
Figura 1.22
VE
R
SIÓ
N
Ejercicio. En la figura 1.23 dé todas las expresiones de ángulos iguales al
\
ángulo AOB.
B
D
O
S
C
Figura 1.23
A
R
1.4. FUNCIONES TRIGONOMÉTRICAS DE ÁNGULOS AGUDOS
25
IM
IN
AR
\ y
En la figura 1.24 se presenta una situación lı́mite: los ángulos AOD
\
DOB son iguales, justamente cuando los cuatro ángulos son ángulos rectos
y las rectas son perpendiculares.
D
O
B
PR
C
EL
A
SIÓ
N
Figura 1.24
1.4
VE
R
Dos ángulos rectos forman un ángulo llano.
Funciones trigonométricas de ángulos agudos
Cuando damos un ángulo agudo, podemos trazar un triángulo rectángulo
que lo tiene como uno de los ángulos internos: Basta con trazar una per\ = α y trazamos
pendicular. En la figura 2.5 hemos pusimos el ángulo AOB
la perpendicular a la recta que contiene a los puntos O y A por el punto B.
26
CAPÍTULO 1. PRELIMINARES
IM
IN
AR
B
α
O
A
R
EL
Figura 1.25
sen α =
|BR|
|OB|
o bien
|BR|
|OR|
cos α =
sen α =
tan α =
cateto adyacente
hipotenusa
cateto opuesto
hipotenusa
cateto opuesto
cateto adyacente
SIÓ
tan α =
|OR|
|OB|
N
cos α =
PR
Las funciones trigonométricas elementales se definen por
VE
R
Como los catetos son menores que la hipotenusa de un triángulo restángulo,
el coseno y el eno de un ángulo agudo son menores que 1.
Es importante señalar que las fracciones que aparecen en la definición
de las funciones trigonométricas no dependen del tamaño del triángulo,
ni de su posición, dependen únicamente del ángulo.
Esto se debe a un resultado de la geometrı́a euclidiana plana: el Teorema
de Thales.
El Teorema de Pitágoras en el triángulo OBR dice que
|OR|2 + |BR|2 = |OB|2 .
27
1.5. FUNCIONES TRIGONOMÉTRICAS
|OR|2
|BR|2
+
=1
|OB|2 |OB|2
IM
IN
AR
Cuando dividimos ambos lados de la igualdad entre |OB|2 obtenemos
y al remplazar las fracciones por las definiciones de las funciones trigonométricas
obtenemos la
EL
IDENTIDAD TRIGONOMÉTRICA FUNDAMENTAL
PR
cos2 α + sen 2 α = 1
Notemos que, a partir de las definiciones, se tiene que
sen α
.
cos α
SIÓ
N
tan α =
1.5
VE
R
En lo que sigue llamaremos funciones trigonométricas elementales de
un ángulo a las funciones cos y sen .
Funciones trigonométricas
Tomemos una circunferencia con centro en el origen y de radio 1. Una semirecta en el primer cuadrante con punto inicial el origen, que forma un ángulo
α con la parte positiva del eje de las abscisas como en la figura 1.x, intersecta
a la circunferencia en un punto Pα (xα , yα ).
28
CAPÍTULO 1. PRELIMINARES
Pα
yα
IM
IN
AR
1
α
O
xα
PR
EL
Figura 1.26
Cuando calculamos las funciones trigonométricas elementales de α obtenemos
yα
xα
= xα sen α =
= yα .
1
1
SIÓ
N
cos α =
VE
R
Es decir, las coordenadas del punto Pα se expresan mediante funciones
trigonométricas. Es por esto que
Definición 1.4: Cı́rculo trigonométrico
La circunferencia con centro en el origen y radio 1 se llama cı́rculo
trigonométrico
Cada posición de una semi-recta con punto inicial en el origen produce
un ángulo entre ella y el eje de las x.
29
1.5. FUNCIONES TRIGONOMÉTRICAS
IM
IN
AR
y
x
EL
Haz click en el eje de las x.
SIÓ
N
PR
Por convención se toma como dirección positiva la contraria a las manecillas del reloj. Se definen las funciones sen y cos de un ángulo α de la manera
siguiente: se ubica el ángulo α como el ángulo formado entre una semi-recta
con punto inicial en el origen y la parte positiva del eje de las x. A continuación se encuentra el punto de intersección de esta semi-recta con la
circunferencia unitaria. La abscisa del punto de intersección es cos α y su
ordenada es sen α.
VE
R
Q(q1 , q2 )
α
β
O
R(r1 , r2 )
Figura 1.27
30
CAPÍTULO 1. PRELIMINARES
Ası́ en la Figura 1.27 tenemos
IM
IN
AR
cos α = q1 sen α = q2
cos β = r1 sen β = r2
Ejemplo 1.10
Calcular las funciones trigonométricas elementales de 120o .
Solución. Solución ◮
Elaboramos la figura correspondiente.
Q
EL
q2
30o
PR
120o
SIÓ
N
q1
O
Figura 1.28
VE
R
Debemos calcular q1 y q2 . Observemos que cos 30o = q2 y que sen 30o = −q1 .
por lo tanto
1
cos 120o = q1 = −sen 30o =
2
y
√
3
o
o
sen 120 = q2 = cos 30 =
.
2
◭
Notemos que si bien a una semi-recta con punto inicial le corresponde
un único punto sobre la circunferencia, el ángulo entre esta semi-recta y el
eje de las x no es único.
En la figura 1.29 se muestra esta situación.
31
β
O
γ
IM
IN
AR
1.5. FUNCIONES TRIGONOMÉTRICAS
R(r1 , r2 )
Figura 1.29
PR
EL
En ella se presentan dos ángulos entre la semi-recta con punto inicial el
origen y que pasa por R : β y γ. Como γ se mueve en la dirección de las
manecillas del reloj, y esto es contrario a la dirección que elegimos, el ángulo
γ es negativo y podemos calcularlo:
γ = −(360o − β) = β − 360o .
SIÓ
N
Esto nos permite calcular también funciones trigonométricas para ángulos
negativos: simplemente nos movemos en la dirección de las manecillas del
reloj.
• Hay un único ángulo en el intervalo [0o , 360o ) asociado a una
semi-recta con punto inicial el origen.
VE
R
• Si dos ángulos producen el mismo punto sobre la circunferencia,
ellos difieren por un número entero de vueltas, tanto en el sentido
de las manecillas del reloj, como en el sentido opuesto. Es decir
la diferencia entre los ángulos es un múltiplo entero de 360o .
• Cuando la diferencia entre dos ángulos es un múltiplo entero de
360o ellos tienen las mismas funciones trigonométricas. Esto se
expresa diciendo que las funciones trigonométricas son periodicas de periodo 360o .
32
CAPÍTULO 1. PRELIMINARES
Ejemplo 1.11
Calcular las funciones trigonométricas del ángulo 3487o .
IM
IN
AR
Solución ◮
Necesitamos ver cuántas vueltas se han dado. Para ello debemos hacer la
división de 4387 entre 360 :
4387 = (12)(360) + 67.
Por lo tanto
cos 4387o = cos 67o ≈ 0.39073
sen 4387o = sen 67o ≈ 0.92050
EL
◭
PR
En general, como las coordenadas de un punto sobre el cı́rculo trigonométrico
no depende de la manera como la semi-recta llegue a él tenemos las siguientes
identidades:
cos(α − 360o ) = cos α
sen (α − 360o ) = sen α
N
cos(α + 360o ) = cos α
sen (α + 360o ) = sen α
La función tangente
SIÓ
No hemos incluido la función tangente dentro de las funciones trigonometricas elementales puesto que podemos calcularla a partir de las otras dos
como observamos antes:
sen α
.
tan α =
cos α
VE
R
Es importante notar que
tan α no está definida cuando cos α = 0.
La función tangente también tiene una interpretación con el cı́rculo
trigonométrico como se muestra en la figura 1.30, donde está el cı́rculo
trigonométrico y la recta tangente a este que pasas por el punto P (1, 0).
1.6. MEDICIÓN DE ÁNGULOS: GRADOS Y RADIANES
r
33
R
IM
IN
AR
β
α
P
O
R′
EL
r′
PR
Figura 1.30
Calculemos tan α en el triángulo OP R :
|P R|
|P R|
=
= |P R| = r
|OP |
1
N
tan α =
SIÓ
puesto que el cı́rculo es unitario. Esto explica por qué no se puede definir
tan 90o : la semi-recta asociada a este ángulo es la parte positiva del eje de
las y que no intersecta a la recta x = 1.
También se tiene que
1.6
|P R′ |
|P R′ |
=−
= −|P R′ | = r ′
|OP |
1
VE
R
tan β = −
Medición de ángulos: grados y radianes
Elegir una unidad es un tanto arbitrario como, por ejemplo, en el caso
de unidades lineales,cuando tenemos varias unidades en uso: el metro o
las pulgadas. Con respecto a los ángulos hay una diferencia porque hay
un ángulo universal: el ángulo recto. En esta sección hablaremos de dos
maneras de medir ángulos.
34
CAPÍTULO 1. PRELIMINARES
1.6.1
Grados
1.6.2
IM
IN
AR
Esta es la manera que hemos usado hasta el momento en este material.
Consiste en dividir el cı́rculo trigonométrico en 360 partes y la unidad será
una de ellas mide 1o .
Radianes
PR
EL
El hecho de que la circunferencia del cı́rculo trigonométrico mide 2π (en las
mismas unidades que se usan para medir el radio del cı́rculo) y se obtiene
con una vuelta completa del eje positivo de las x, permite otra manera de
medir los ángulos: midiendo el arco que ellos delimitan. Ası́, si el arco que
delimita el ángulo α, medido con la misma unidad con la que se midió el
radio, mide a entonces decimos (es una definición)que el ángulo α mide a
radianes. (Recordemos que estamos en el cı́rculo unitario.)
1
a
α
SIÓ
N
O
Figura 1.31
VE
R
Ası́ el ángulo de 360o delimita la circunferencia completa y por lo tanto
mide 2π radianes. Además, si el arco mide 1, el ángulo que él delimita mide
1 radián.
Ejemplo 1.12
Encontrar la medida en grados del ángulo que mide π radianes y del que
mide π/2.
Solución ◮
1.7. OTRAS IDENTIDADES TRIGONOMÉTRICAS
35
El ángulo que mide π radianes describe media circunferencia. Por lo tanto
mide 180o . El ángulo que mide π/2 radianes describe un cuarto de circunferencia. Entonces mide 90o .
◭
IM
IN
AR
En general, si el ángulo α mide a radianes, entonces describe un arco de
a
2π
por lo tanto debe ser esa misma fracción de la circunferencia completa. Es
decir
o
a
360 .
a rd ∼
2π
Ejemplo 1.13
Encontrar la medida en grados del ángulo que mide 1 radián.
1.7
PR
EL
Solución ◮
Por lo que vimos antes el ángulo de 1 rd mide
360 o
aprox. 57.3o
2π
◭
Otras identidades trigonométricas
SIÓ
N
De la definición de las funciones trigonométricas para ángulos agudos se
desprenden algunas identidades cuando α es agudo:
cos(α) = sen (90o − α)
sen (α) = cos (90o − α).
Hay identidades que tienen que ver con la definción de las funciones trigonométricas
para ángulos arbitrarios como
VE
R
cos(α + 180o ) = − cos α
sen (α + 180o ) = −sen α
Estas identidades se mantienen para ángulos arbitrarios.
Hay identidades de otra naturaleza como las que dan la manera de calcular las funciones trigonométricas de sumas y diferencias de ángulos
cos (α + β)
sen (α + β)
cos (α − β)
sen (α − β)
=
=
=
=
cos α cos β − sen αsen β
sen α cos β + cos αsen β
cos α cos β + sen αsen β
sen α cos β − cos αsen β
36
CAPÍTULO 1. PRELIMINARES
Definimos
sec α =
1
cos α
cosec α =
1
sen α
cotan α =
1
tan α
IM
IN
AR
tenemos identidades del mismo tipo de la identidad fundamental:
1 + tan2 α = sec2 α
1 + cotan 2 α = cosec 2 α
1.8
Algunas consideraciones sobre coseno y seno
Después de la discusión anterior, podemos calcular las funciones coseno y
seno para cualquier número. En general cuando se hace esto los números
que miden el ángulo se miden en radianes.
La funcion coseno
EL
1.8.1
En la figura 1.32 está la gráfica de la función coseno para ángulos α ∈ [0, π]
y que toma valores en el intervalo [−1, 1]
PR
y
1
b
b
b
b
b
b
VE
R
SIÓ
N
b
b
α
b
π
π/2
b
u
b
b
b
b
b
−1
b
Figura 1.32
y = cos x
b
x
1.8. ALGUNAS CONSIDERACIONES SOBRE COSEN O Y SEN O 37
Para cada α ∈ [0, π] hay un único u ∈ [−1, 1] de manera que
Esto se escribe también
α = arccos u.
1.8.2
La funcion seno
IM
IN
AR
u = cos α.
También hemos elaborado la gráfica de la función seno para ángulos α ∈
[0, π]. Para estos valors del ángulo el seno está en el intervalo [0, 1].
y
b
b
b
1
b
b
b
EL
b
b
b
PR
u
b
b
b
α
N
π/2
SIÓ
Figura 1.33
y = sen x
tales que
VE
R
Además para cada valor en u ∈ [0, 1) hay dos ángulos
π i
h π
y π−α∈
,π
α ∈ 0,
2
2
sen α = sen (π − α) = u.
Además π/2 es el único ángulo en [0, π] con
sen
π
= 1.
2
b
b
b
b
b
(π − α)π
x