El plano de Moulton M es la geometrıa de incidencia

El plano de Moulton M es la geometrı́a de incidencia definida en el plano Euclı́deo R2 como sigue: los
puntos de M son los puntos de R2 , el plano es todo el conjunto y las rectas de M son de tres tipos: las
verticales, las de pendiente no negativa y las quebradas. Es decir, el conjunto de rectas es
L = {La : a ∈ R} ∪ {Lm,b : m ≥ 0, b ∈ R} ∪ {Mm,b : m < 0, b ∈ R},
donde La tiene ecuación x = a, Lm,b tiene ecuación y = mx + b y la recta Mm,b tiene ecuación
(
mx + b si x < 0,
y=
2mx + b si x ≥ 0
Las rectas Mm,b se llaman rectas quebradas pues se quiebran en el eje y.
1. Verifique que el plano de Moulton satisface los axiomas de incidencia y compruebe que esta geometrı́a
es afı́n.
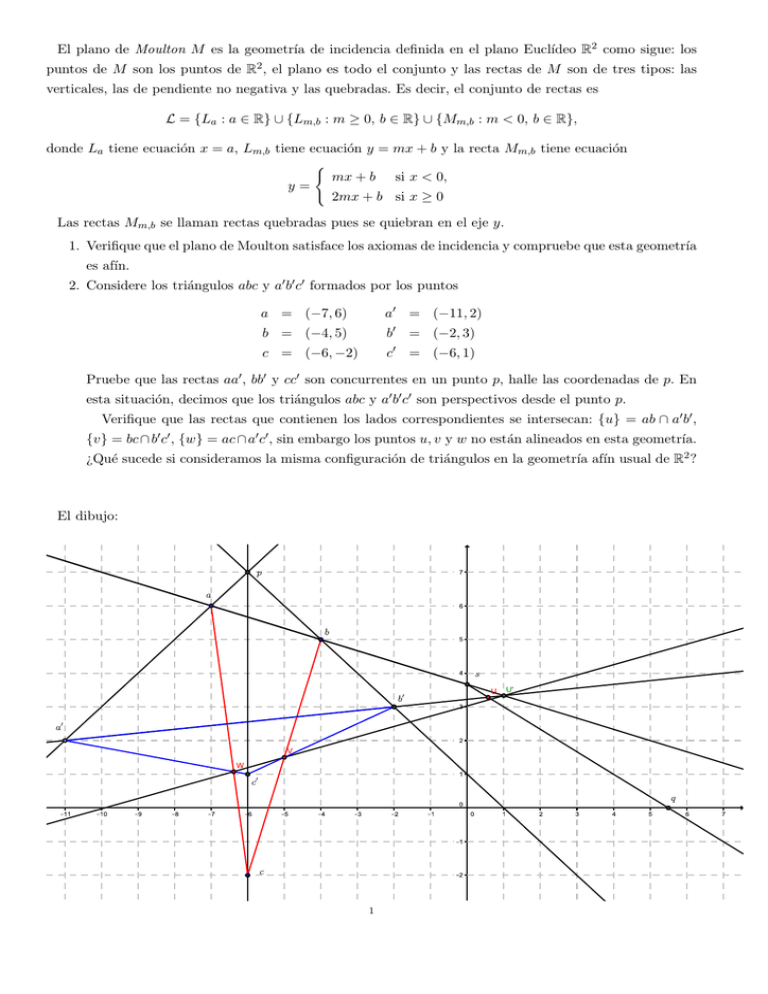
2. Considere los triángulos abc y a′ b′ c′ formados por los puntos
a = (−7, 6)
a′ = (−11, 2)
b = (−4, 5)
b′ = (−2, 3)
c = (−6, −2)
c′ = (−6, 1)
Pruebe que las rectas aa′ , bb′ y cc′ son concurrentes en un punto p, halle las coordenadas de p. En
esta situación, decimos que los triángulos abc y a′ b′ c′ son perspectivos desde el punto p.
Verifique que las rectas que contienen los lados correspondientes se intersecan: {u} = ab ∩ a′ b′ ,
{v} = bc ∩ b′ c′ , {w} = ac ∩ a′ c′ , sin embargo los puntos u, v y w no están alineados en esta geometrı́a.
¿Qué sucede si consideramos la misma configuración de triángulos en la geometrı́a afı́n usual de R2 ?
El dibujo:
1
2
Las ecuaciones de las rectas del triángulo abc:
↔
↔
ab es la recta quebrada M− 1 , 11 , es decir ab tiene ecuación:
3 3
(
− 13 x + 11
si x < 0,
3
y=
11
2
− 3 x + 3 si x ≥ 0
↔
↔
ac es la recta quebrada M−8,−50 , es decir ac tiene ecuación:
(
−8x − 50 si x < 0,
y=
−16x − 50 si x ≥ 0
↔
↔
bc es la recta L 7 ,19 , es decir bc tiene ecuación:
2
7
y = x + 19
2
′
Las rectas que contienen los lados del triángulo a b′ c′ tienen ecuaciones:
↔
↔
a′ b′ es la recta L 1 , 29 , es decir a′ b′ tiene ecuación:
9
9
1
29
y = x+
9
9
↔
↔
a′ c′ es la recta quebrada M− 1 ,− 1 , es decir a′ c′ tiene ecuación:
5
5
(
− 51 x − 15 si x < 0,
y=
− 52 x − 15 si x ≥ 0
↔
↔
b′ c′ es la recta L 1 ,4 , es decir b′ c′ tiene ecuación:
2
1
y = x+4
2
Los puntos de intersección etre los lados son:
↔
4 23
donde u( , )
7 7
↔
↔
3
{v} =bc ∩ b′ c′ , donde v(−5, )
2
↔
83
14
↔
{w} =ac ∩ a′ c′ , donde w(− , )
13 13
→
→
Para estudiar si estos tres puntos están alineados o no, veremos si los vectores uv y vw son paralelos.
↔
{u} =ab ∩ a′ b′ ,
Tenemos
18 11
39 25
→
,− )
vw= (− , − )
7
14
13 26
18
25
11
los cuales no son paralelos pues − 39
/(−
)
=
6
−
/(−
).
7
13
14
26
→
uv= (−
↔
Para ver qué sucede en la geometrı́a euclı́dea usual, tenemos que cambiar la recta ab= M− 1 , 11 por
3
↔′
ab = L− 1 , 11 y vemos que
3
3
↔′
↔
{u′ } =ab ∩ a′ b′ ,
→
donde u′ (1,
→
Ahora el vector u′ v= (−6, 11
6 ) que al compararlo con vw resulta
→
→
u′ v // vw;
por lo tanto u′ , v y w sı́ están alineados.
10
).
3
3