ER-CS-01: EJERCICIO DE CORTANTE SIN ARMADURA A

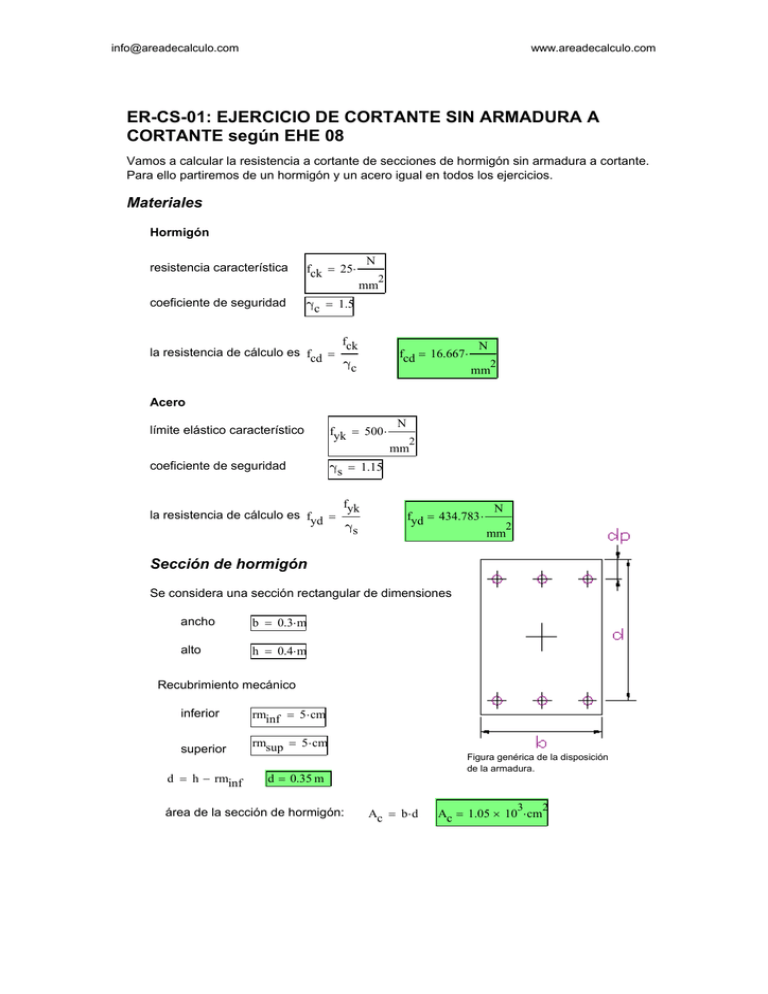
[email protected]
www.areadecalculo.com
ER-CS-01: EJERCICIO DE CORTANTE SIN ARMADURA A
CORTANTE según EHE 08
Vamos a calcular la resistencia a cortante de secciones de hormigón sin armadura a cortante.
Para ello partiremos de un hormigón y un acero igual en todos los ejercicios.
Materiales
Hormigón
resistencia característica
N
fck = 25⋅
2
mm
coeficiente de seguridad
γc = 1.5
fck
la resistencia de cálculo es fcd =
γc
fcd = 16.667⋅
N
2
mm
Acero
límite elástico característico
fyk = 500 ⋅
N
2
mm
coeficiente de seguridad
γs = 1.15
fyk
la resistencia de cálculo es fyd =
γs
fyd = 434.783 ⋅
N
2
mm
Sección de hormigón
Se considera una sección rectangular de dimensiones
ancho
b = 0.3⋅ m
alto
h = 0.4⋅ m
Recubrimiento mecánico
inferior
rminf = 5 ⋅ cm
superior
rmsup = 5 ⋅ cm
d = h − rminf
Figura genérica de la disposición
de la armadura.
d = 0.35 m
área de la sección de hormigón:
Ac = b ⋅ d
3
Ac = 1.05 × 10 ⋅ cm
2
[email protected]
www.areadecalculo.com
La sección no tiene armadura a cortante, por ello la
comprobación de AGOTAMIENTO POR COMPRESIÓN
OBLICUA DEL ALMA, Vu1 no sería necesaria.
Área de la armadura longitudinal de tracción
anclada como indica la figura:
Asl = 12⋅ cm
2
ángulo de las armaduras transversales de la pieza:
α = 90.⋅ deg
ángulo de las bielas de compresión con el eje de la pieza :
θ = 45⋅ deg
áncho de la pieza (en este caso es de ancho constante) :
bo = b
esfuerzo axil de cálculo, (positivo es compresión):
Nd = 400kN
Tensión de compresión axil efectiva. En
pilares debe calcularse teniendo en cuenta la
compresión absorvida por las armadures
comprimidas. En nuestro ejemplo se
desprecia.
σpcd =
Nd
Ac
N
σpcd = 3.81⋅
2
mm
Obtención de Vu1
A partir de los datos anteriores, obtenemos una serie de valores necesarios para la fórmula
final:
coeficiente de reducción por efecto del esfuerzo axil:
N
σpcd = 3.81⋅
2
fcd = 16.667⋅
mm
k =
1 if σpcd ≤ 0
1+
σpcd
fcd
⎛
⎝
N
2
mm
if σpcd > 0 ∧ σpcd ≤ 0.25⋅ fcd
0.5⋅ fcd = 8.333 ⋅
N
2
mm
σpcd ⎞
fcd
⎟ otherwise
⎠
⎛
2.5⋅ ⎜ 1 −
⎝
k = 1.229
2
mm
0.25⋅ fcd = 4.167 ⋅
1.25 if 0.25⋅ fcd < σpcd ∧ σpcd ≤ 0.5⋅ fcd
2.5⋅ ⎜ 1 −
N
σpcd ⎞
fcd
⎟ = 1.929
⎠
[email protected]
www.areadecalculo.com
fck
⎛
⎜
N
⎜
2
mm
faux = ⎜ 0.9 −
200
⎝
flcd =
⎞
⎟
⎟
⎟ ⋅f
⎠ cd
faux = 12.917⋅
N
2
mm
N
0.6⋅ fcd if fck ≤ 60⋅
2
mm
N
faux if fck > 60⋅
∧ faux < 0.5⋅ fcd
2
mm
N
flcd = 10⋅
0.5⋅ fcd otherwise
2
mm
Finalmente obtenemos la resistencia por agotamiento por compresión oblicua del alma:
Vu1 = flcd⋅ b o ⋅ d ⋅ k ⋅
cot( θ) + cot( α)
1 + cot( θ)
2
Vu1 = 645 ⋅ kN
En los casos habituales de armaduras con cercos o estribos y con axiles despreciables,
la fórmula final es:
cot( α) = 0
cot( θ) = 1
cot( θ) + cot( α)
1 + cot( θ)
Vu1p = 0.3⋅ fcd⋅ b o ⋅ d
2
= 0.5
Vu1p = 525 ⋅ kN
La diferencia es debida al axil de tracción aplicado inicialmente, que no se ha considerado
en la fórmula reducida.
[email protected]
www.areadecalculo.com
Obtención de Vu2 (= Vcu en este caso) en zonas fisuradas a flexión
(Para zonas no fisuradas se utiliza otra formulación. Consultar EHE 08)
Ahora realizamos la comprobación de agotamiento por
tracción del alma.
Al utilizar fórmulas que obligan a unas unidades específicas,
preparamos las variables adecuadamente:
d mm =
2
d
mm
d mm = 350
mm
fckNmm = fck⋅
fckNmm = 25
N
Cuantía geométrica de la armadura longitudinal de tracción:
Asl
ρl.aux =
Ac
ρl =
ρl.aux = 0.011
0.02 if ρl.aux ≥ 0.02
ρl = 0.011
ρl.aux otherwise
Coeficiente (efecto de áridos en canto útil):
⎛
ξaux = ⎜ 1 +
⎝
⎞ ξ= ξ
⎟
aux if ξaux < 2
d mm
⎠
200
ξ = 1.756
2 otherwise
Resistencia virtual a cortante fcv:
γc = 1.5
1
(
)
0.18
3 N
fcv.old =
⋅ ξ⋅ 100 ⋅ ρl⋅ fckNmm ⋅
2
γc
mm
3
1⎞
⎛
⎜ 0.075 2
2. ⎟ N
fcvaux = ⎜
⋅ ξ ⋅ fckNmm ⎟ ⋅
⎝ γc
⎠ mm2
(
)
fcv.final = max fcv.old , fcvaux
N
fcv.old = 0.644 ⋅
2
mm
N
fcvaux = 0.582 ⋅
2
mm
fcv.final = 0.644 ⋅
N
2
mm
[email protected]
σpcd_v2 =
www.areadecalculo.com
σpcd if σpcd < 0.3⋅ fcd
σpcd = 3.81⋅ MPa
12⋅ MPa if σpcd > 12⋅ MPa ∧ 0.3⋅ fcd > 12⋅ MPa
0.3⋅ fcd = 5 ⋅ MPa
0.3⋅ fcd otherwise
(
σpcd_v2 = 3.81⋅ MPa
)
Vu2 = fcv.final + 0.15⋅ σpcd_v2 ⋅ b o ⋅ d
Vu2 = 127.638 ⋅ kN
Comparado con Vu1 vemos que Vu2 es mucho mas restrictivo en este caso (sin
armadura a cortante).
RECUERDE: PUEDE REALIZAR ESTOS CÁLCULOS MÁS FÁCILMENTE CON
www.areadecalculo.com