Diseño de elementos de acero sujetos a tensión Diseño por tensión

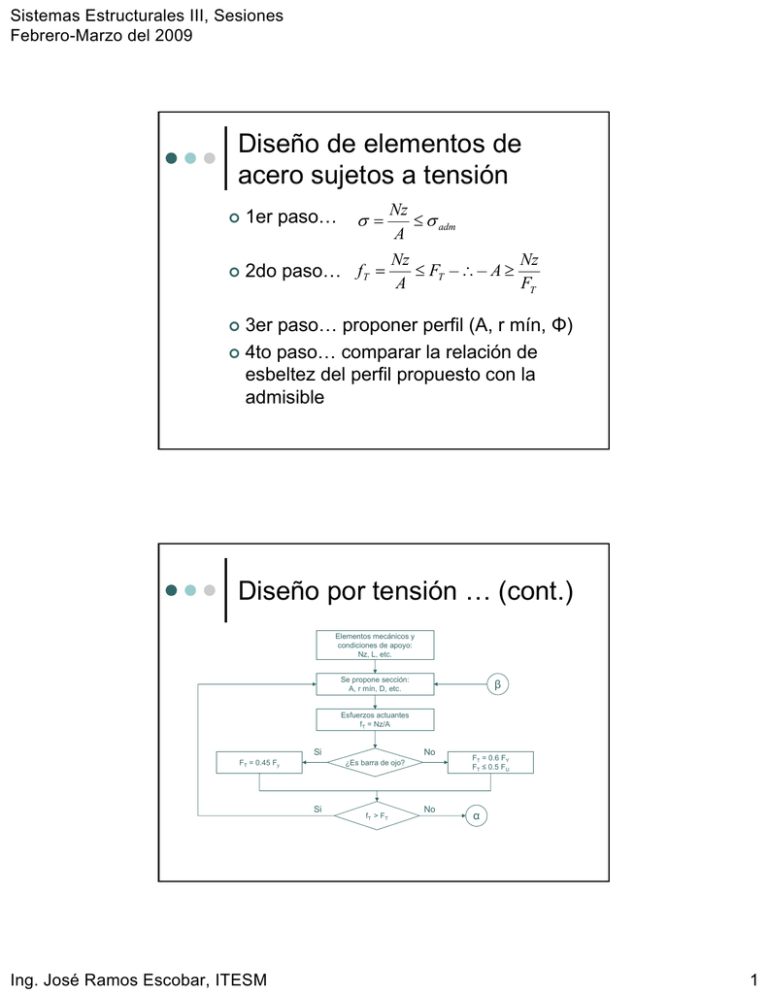
Sistemas Estructurales III, Sesiones
Febrero-Marzo del 2009
Diseño de elementos de
acero sujetos a tensión
|
1er paso…
|
2do paso… fT =
σ=
Nz
≤ σ adm
A
Nz
Nz
≤ FT ∴ A ≥
FT
A
3er paso… proponer perfil (A, r mín, Φ)
| 4to paso… comparar la relación de
esbeltez del perfil propuesto con la
admisible
|
Diseño por tensión … (cont.)
Elementos mecánicos y
condiciones de apoyo:
Nz, L, etc.
Se propone sección:
A, r mín, D, etc.
β
Esfuerzos actuantes
fT = Nz/A
Si
FT = 0.45 Fy
Si
Ing. José Ramos Escobar, ITESM
No
¿Es barra de ojo?
fT > FT
No
FT = 0.6 FY
FT ≤ 0.5 FU
α
1
Sistemas Estructurales III, Sesiones
Febrero-Marzo del 2009
Diseño por tensión … (cont.)
α
β
No
P
Es
L/ r mín < 240
Principal,
Secundario o
redondo
R
Es
L/D < 500
S
Si
β
No
No
β
Si
Es
L/ r mín < 300
Si
β
Es
Económica?
No
|
Si
Fin
Acero A36:
Fy = 2,530 Kg/cm²
0.6 Fy = 1,520 Kg/cm²
0.5 FU = 2,100 Kg/cm²
Diseño de columnas
(elementos a compresión)
|
|
|
|
|
|
|
Similar a los elementos a tensión, depende de la
tendencia al pandeo
El pandeo depende de la longitud, geometría,
condiciones de apoyo, defectos de laminación, etc
Ver Capítulo E del ASD/AISC (pág. 5-42)
El factor K dependerá de la forma de apoyo en los
extremos (Tabla C-C2.1 pag. 5-135)
El factor Cc determina la frontera entre el pandeo
elástico e inelástico (límite de proporcionalidad sesiones
1 y 2) para el A-36 -> Cc=126
El cálculo inicia suponiendo un esfuerzo fz según las
fórmulas del capítulo E
Se propone un perfil y se verifica si cumple con las
siguientes especificaciones
Ing. José Ramos Escobar, ITESM
2
Sistemas Estructurales III, Sesiones
Febrero-Marzo del 2009
Diseño de elementos de
acero sujetos a compresión
|
1er paso… suponer fz
|
2do paso… A ≥
Nz
fZ
3er paso… proponer perfil (A, r mín, Φ)
| 4to paso… revisar esbeltez del perfil y
esfuerzos admisibles
|
Diseño por compresión …
(cont.)
Elementos mecánicos y
condiciones de apoyo:
Nz, L, K, Fy, etc.
Se propone esfuerzo fz
A = Nz/fz
Se propone perfil
A, r mín, D, etc.
α
No
¿Es Kl/r ≤ 200?
β
fZ
⎛
⎜
⎜
= ⎜1 −
⎜
⎜
⎝
Ing. José Ramos Escobar, ITESM
⎛ Kl ⎞
⎜
⎟
⎝ r ⎠
2 Cc 2
2
⎞
⎟
⎟ Si
⎟ Fy
⎟
⎟
⎠
Si
No
¿Es Kl/r < Cc?
fZ =
12 π 2 E
23 ⎛ Kl ⎞ 2
⎜
⎟
⎝ r ⎠
β
3
Sistemas Estructurales III, Sesiones
Febrero-Marzo del 2009
Diseño por compresión …
(cont.)
Si no se
Especifica
otro F.S.
β
⎛ Kl ⎞
⎛ Kl ⎞
⎜
⎟
⎜
⎟
5 3 r ⎠ 1 ⎝ r ⎠
F .S . = + ⎝
−
3 8 Cc
8 Cc 3
fZ =
3
fZ
F .S .
Si
¿ Es Secundario?
No
¿Es
Kl/ r < 120 ?
No
fZ =
fZ
l ⎞
⎛
1
.
6
−
⎜
⎟
200 r ⎠
⎝
Si
FA = Nz / A
Si
¿Es
FA < fZ ?
Acero A36:
E = 2.1 x 106 Kg/cm²
Cc = 126
FY = 2,530 Kg/cm²
No
α
Si
¿Es el más
económico ?
Fin
No
α
Diseño de trabes (elementos
a flexión)
|
|
|
|
|
|
|
|
Un elemento sujeto a flexión depende de su resistencia al
pandeo y este varía de acuerdo a la sección propuesta
Debe verificarse su resistencia al corte la cual depende de la
sección transversal del perfil propuesto
Ver Capítulo F del ASD/AISC (pág. 5-45)
Observe que el análisis depende de la sección si es un IPR o
sección cajón o bien un CPS (canal) u otro
Cada perfil deberá revisarse por “compacidad”, es decir, si la
sección es compacta o no compacta (ver Tabla B5.1 pag. 5-36)
El cálculo inicia con la propuesta de un perfil que cumpla con el
área por corte y el módulo “S” que resista el momento actuante
Otro aspecto que puede revisarse al inicio es la flecha máxima
Los límites por deformación (aplastamiento) deben ser
revisados en los apoyos
Ing. José Ramos Escobar, ITESM
4
Sistemas Estructurales III, Sesiones
Febrero-Marzo del 2009
Diseño de elementos de
acero sujetos a flexión
|
1ro proponer un perfil que cumpla con:
σ max = ±
SX =
|
MX
M
y± Y x
IX
IY
IX
M
∴σ max = X
ymax
SX
SX =
MX
σ max
Asegurarse de revisar flecha máxima:
δ max ≤
L
360
Diseño por flexión … (cont.)
|
Por esfuerzo cortante:
τ max =
|
Vmax
≤ 0.4 FY
Aalma
Aalma ≥
Vmax
0.4 FY
Por aplastamiento:
Apoyo extremo
N≥
R
−K
0.75FY (tw)
Ing. José Ramos Escobar, ITESM
Apoyo intermedio
N≥
R
− 2K
0.75 FY (tw)
5
Sistemas Estructurales III, Sesiones
Febrero-Marzo del 2009
Entendiendo los esfuerzos
Y
MX
M
y± Y x
IX
IY
I
M
S X = X ∴σ max = X
ymax
SX
σ max = ±
V
MY
X
SX =
MX
σ max
τ max =
V
MX
Vmax
≤ 0.4 FY
Aalma
V
Aalma ≥ max
0.4 FY
Entendiendo “aplastamiento”
Proyección a 45°
Proyección a 45°
área crítica por
aplastamiento
R
−K
0.75 FY (tw)
Ing. José Ramos Escobar, ITESM
k
n
n+k
N≥
k
n
N≥
tw
R
− 2K
0.75FY (tw)
k
6
Sistemas Estructurales III, Sesiones
Febrero-Marzo del 2009
Diseño por flexión … (cont.)
|
Requisitos de “compacidad” (de la Tabla
B5.1 convertidos a sistema MKS)
1. Los patines se conectan al o las
almas en forma continua
bf
2. Para secciones “I”
2t f
3. Para secciones cajón
bf
tf
≤
545
Fy
≤
1593
Fy
Diseño por flexión … (cont.)
|
Requisitos de “compacidad” (cont…)
4. Para secciones “I”
NZ
A
d 2155
si
≤
tw
Fy
FA
> 0.16
Fy
d 5366 ⎡
FA ⎤
≤
⎢1 − 3.74 ⎥ si
tw
Fy ⎦⎥
Fy ⎣⎢
FA
≤ 0.16
Fy
FA =
5. Para secciones “I”
L≤
Ing. José Ramos Escobar, ITESM
637b f
Fy
y L≤
1.4 × 10 6
d
Fy
Af
7
Sistemas Estructurales III, Sesiones
Febrero-Marzo del 2009
Diseño por flexión … (cont.)
|
Requisitos de “compacidad” (cont…)
6. Para secciones tubulares
D 231917
≤
e
FY
7. Una sección cajón es compacta si:
d ≤ 6b
⎛
M ⎞ b
L ≤ ⎜⎜137100 + 84370 1 ⎟⎟
M 2 ⎠ FY
⎝
y t f ≤ 2t w
pero no necesariamente menor a:
L ≥ 84370
b
FY
Diseño por flexión … (cont.)
Elementos mecánicos y
condiciones de apoyo:
M1 ; M2 ; M3 ; L ; V ; My
Sección propuesta (geometría):
Sx, Sy, rb, d, tw, etc.
α
Si
¿Es sección I ?
Tipo IPR
No
Si
Tipo cajón
¿Es sección cajón?
No
Si
¿Es sección canal?
Tipo canal
No
β
Ing. José Ramos Escobar, ITESM
8
Sistemas Estructurales III, Sesiones
Febrero-Marzo del 2009
Diseño por flexión … (cont.)
β
Fbx = 0.6 Fy
Fby = 0.6 Fy
L ≤ 637 bf / √Fy
fbx = Mx / Sx
fby = My / Sy
α
No
fbx/Fbx + fby/Fby < 1
Si
Esfuerzo cortante (fv) = V / A
Fv = 0.4 Fy
No
α
Si
fv < Fv
Yreal<Yadm
No
α
Si
α
No
Si
¿Es económica?
Fin
Diseño por flexión … (cont.)
secciones tipo “IPR”
Tipo IPR
Si
¿es compacta?
⎡
⎤
⎛ bf ⎞
⎟⎟ fY ⎥ FY Si
fbX = ⎢0.79 − 0.000239⎜⎜
⎝ 2tf ⎠
⎣
⎦
⎡
⎤
⎛ bf ⎞
fbY = ⎢1.75 − 0.000597⎜⎜
⎟⎟ fY ⎥ FY
⎝ 2tf ⎠
⎣
⎦
Fbx = 0.66 Fy
Fby = 0.75 Fy
No
bf
796
≤
2t f
Fy
No
No
bf
545
≤
2t f
Fy
Si
Fby = 0.6 Fy
Regresar a la
revisión principal
Fbx = 0.6 Fy
Cb = 1.75 + 1.05(M 1 M 2 ) + 0.3(M 1 M 2 ) ≤ 2.3
Si
7172×103 • Cb
L
≤
rb
fY
No
2
rb=radio de giro; M1 y M2 momentos entre los que hay un
momento máximo; si hay un momento mayor Cb = 1
Ing. José Ramos Escobar, ITESM
φ
9
Sistemas Estructurales III, Sesiones
Febrero-Marzo del 2009
Diseño por flexión …secciones
tipo “IPR” (cont…)
φ
fbX 1 =
⎡11950 × 103 • Cb ⎤
fbX 2 = ⎢
(L rb )2 ⎥⎦
⎣
Si
fbx1 > fbx2
No
843700 • Cb
L (d A f )
Si
35850 × 103 • Cb
L
≤
rb
fY
Fbx = fbx2
2
⎡2
⎤
f Y (L rb )
fbX 2 = ⎢ −
⎥ Fy
3
Cb
3
107570
10
×
•
⎣
⎦
fbx > 0.6 FY
No
Si
FbX = 0.6 Fy
No
Fbx = fbx1
Regresar a la
revisión principal
Diseño por flexión … (cont.)
secciones “cajón” y “canal”
Tipo Canal
Tipo Cajón
Si
¿es compacta?
Fbx = 0.66 Fy
Fby = 0.66 Fy
No
fbX =
843700 • Cb
L(d A f )
fbY = 0.6 FY
Fbx = 0.6 Fy
Fby = 0.6 Fy
Regresar a la
revisión principal
fbx > 0.6 FY
Si
FbX = 0.6 Fy
No
Regresar a la
revisión principal
Ing. José Ramos Escobar, ITESM
10
Sistemas Estructurales III, Sesiones
Febrero-Marzo del 2009
Elementos sujetos a
esfuerzos combinados
Un elemento sujeto a flexo-compresión o
flexo-tensión es aquel que soporta
cargas axiales + cargas transversales
| A flexo-compresión debe cumplir que:
|
MX
M
CMY Y
Nz A
SX
SY
+
+
≤1
FA
⎛ Nz A ⎞
⎛ Nz A ⎞
⎜⎜1 −
⎟⎟ f bx ⎜1 −
⎟ f by
⎜
⎟
F
'
'
F
ex ⎠
⎝
ey ⎠
⎝
CMX
Ejemplo columna
Debe cumplirse para toda la sección
“para gente grande”
Elementos sujetos a esfuerzos
combinados… (cont.)
|
En los extremos debe cumplirse que:
Nz A M X S X M Y SY
+
+
≤1
0.6 FY
f bx
f by
|
Cuando
NZ A
≤ 0.15
FA
solo se verifica que:
Nz A f bx f by
+
+
≤1
FA
Fbx Fby
Ing. José Ramos Escobar, ITESM
11
Sistemas Estructurales III, Sesiones
Febrero-Marzo del 2009
Elementos sujetos a esfuerzos
combinados… (cont.)
|
De las anteriores expresiones, se tiene:
12π 2 E
10'480,000
F 'e =
=
2
(Kl X rX )2
13(Klb rb )
FA = esfuerzo admisible a compresión
como si solo hubiera compresión
| fbx y fbx = esfuerzos admisibles de flexión
como si solo hubiera flexión
|
Elementos sujetos a esfuerzos
combinados… (cont.)
Cmx y Cmy = factores de modificación que
contrarestan factores de amplificación,
dependen de las cargas transversales y
de la posibilidad de desplazamientos
(ver tabla C-H1.1 pág. 5-154)
| Cmx y Cmy = 0.85 si hay desplazamientos
relativos en los extremos
| Cmx = 0.6 -0.4 (M1/ M2) ≥ 0.4 si no hay
desplazamientos ni cargas transversales
|
Ing. José Ramos Escobar, ITESM
12
Sistemas Estructurales III, Sesiones
Febrero-Marzo del 2009
Elementos sujetos a esfuerzos
combinados… (cont.)
M1 = Momento menor
| M2 = Momento mayor
| Si los desplazamientos lineales están
impedidos y hay cargas transversales,
ver fórmulas C-H1-6 y C-H1-7 así como
la tabla C-H1.1 en págs. 5-153 y 5-154
|
Ing. José Ramos Escobar, ITESM
13