Diseño de elementos de acero sujetos a tensión Diseño por tensión

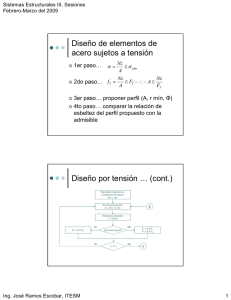
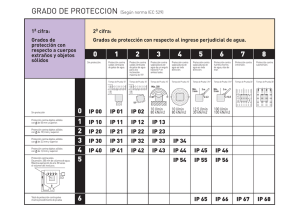
Sistemas Estructurales III, Sesiones
Enero-Febrero del 2009
Diseño de elementos de
acero sujetos a tensión
|
1er paso…
|
2do paso… fT =
σ=
Nz
≤ σ adm
A
Nz
Nz
≤ FT ∴ A ≥
FT
A
3er paso… proponer perfil (A, r mín, Φ)
| 4to paso… comparar la relación de
esbeltez del perfil propuesto con la
admisible
|
Diseño por tensión … (cont.)
Elementos mecánicos y
condiciones de apoyo:
Nz, L, etc.
Se propone sección:
A, r mín, D, etc.
β
Esfuerzos actuantes
fT = Nz/A
Si
FT = 0.45 Fy
Si
Ing. José Ramos Escobar, ITESM
No
¿Es barra de ojo?
fT > FT
No
FT = 0.6 FY
FT ≤ 0.5 FU
α
1
Sistemas Estructurales III, Sesiones
Enero-Febrero del 2009
Diseño por tensión … (cont.)
α
β
No
P
Es
L/ r mín < 240
Principal,
Secundario o
redondo
R
Es
L/D < 500
S
Si
β
No
No
β
Si
Es
L/ r mín < 300
Si
β
Es
Económica?
No
|
Si
Fin
Acero A36:
Fy = 2,530 Kg/cm²
0.6 Fy = 1,520 Kg/cm²
0.5 FU = 2,100 Kg/cm²
Diseño de columnas
(elementos a compresión)
|
|
|
|
|
|
|
Similar a los elementos a tensión, depende de la
tendencia al pandeo
El pandeo depende de la longitud, geometría,
condiciones de apoyo, defectos de laminación, etc
Ver Capítulo E del ASD/AISC (pág. 5-42)
El factor K dependerá de la forma de apoyo en los
extremos (Tabla C-C2.1 pag. 5-135)
El factor Cc determina la frontera entre el pandeo
elástico e inelástico (límite de proporcionalidad sesiones
1 y 2) para el A-36 -> Cc=126
El cálculo inicia suponiendo un esfuerzo fz según las
fórmulas del capítulo E
Se propone un perfil y se verifica si cumple con las
siguientes especificaciones
Ing. José Ramos Escobar, ITESM
2
Sistemas Estructurales III, Sesiones
Enero-Febrero del 2009
Diseño de elementos de
acero sujetos a compresión
|
1er paso… suponer fz
|
2do paso… A ≥
Nz
fZ
3er paso… proponer perfil (A, r mín, Φ)
| 4to paso… revisar esbeltez del perfil y
esfuerzos admisibles
|
Diseño por compresión …
(cont.)
Elementos mecánicos y
condiciones de apoyo:
Nz, L, K, Fy, etc.
α
Se propone esfuerzo fz
A = Nz/fz
Se propone perfil
A, r mín, D, etc.
No
¿Es Kl/r ≤ 200?
β
fZ
⎛
⎜
⎜
⎜1 −
⎜⎜
= ⎝
Ing. José Ramos Escobar, ITESM
⎛ Kl ⎞
⎜
⎟
⎝ r ⎠
2 Cc 2
2
⎞
⎟
⎟
⎟ Fy
⎟⎟
⎠
Si
No
Si
¿Es Kl/r < Cc?
fZ =
12 π 2 E
23 ⎛ Kl ⎞ 2
⎜
⎟
⎝ r ⎠
β
F .S .
3
Sistemas Estructurales III, Sesiones
Enero-Febrero del 2009
Diseño por compresión …
(cont.)
Si no se
Especifica
otro F.S.
β
⎛ Kl ⎞
⎛ Kl ⎞
⎜
⎟
⎜
⎟
5 3 r ⎠ 1 ⎝ r ⎠
F .S . = + ⎝
−
3 8 Cc
8 Cc 3
¿ Es Secundario?
Si
No
3
¿Es
Kl/ r < 120 ?
No
fZ =
fZ
l ⎞
⎛
⎜ 1 .6 −
⎟
200 r ⎠
⎝
Si
FA = Nz / A
¿Es
FA < fZ ?
α
Acero A36:
No
E = 2.1 x 106 Kg/cm²
Cc = 126
FY = 2,530 Kg/cm²
Si
α
Ing. José Ramos Escobar, ITESM
No
¿Es
económico ?
Si
Fin
4