Dada la función f(x) = x2 – 4x. (a) Encuentra la primitiva F de f

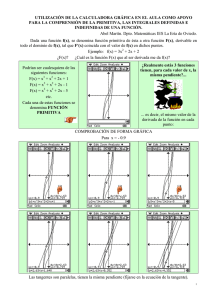
www.aulamatematica.com
1
43 – PAU – Universidad de Oviedo – Fase General – Opción B – junio 2010
Dada la función f(x) = x2 – 4x.
(a) Encuentra la primitiva F de f verificando que F(3) = 0.
(b) Representa gráficamente la función f y calcula el área limitada por la curva
y el eje X entre x = 1 y x = 7.
RESOLUCIÓN apartado (a)
• Encuentra la primitiva F de f verificando que F(3) = 0.
Dada una función f(x), se denomina función primitiva de ésta a otra función F(x), derivable
en todo el dominio de f(x), tal que F'(x) coincida con el valor de f(x) en dichos puntos.
F(x) = ¿?
F ’(x) = f(x)
f(x) = x2 – 4x
Calculemos la primitiva F(x)
∫ (x2 – 4x) dx =
= ∫ x2 dx – ∫ 4x dx =
x3
x2
–4
→
3
2
x3
F(x) =
– 2x2 + k
3
=
F(3) = 0
33
– 2 · 32 + k = 0
3
9 – 18 + k = 0
k=9
La primitiva F(x) que verifica las condiciones del enunciado es:
x3
F(x) =
– 2x2 + 9
3
RESOLUCIÓN apartado (b)
Representa gráficamente la función f y calcula el área limitada por la curva y el eje X entre
x = 1 y x = 7.
f(x) = x2 – 4x se trata de una parábola. Obtenemos la tabla de valores y, ayudándonos
de las propiedades obvias del estudio local, representamos la función...
V(–b/2a, y) → V (2, y)
2
y = x – 4x
x
y
2
–4
1
–3
3
–3
0
0
4
0
Vértice (2, – 4)
Puntos de corte de la parábola con el eje OX
x2 – 4x = 0
x (x – 4) = 0
x1 = 0 ; x2 = 4
 Abel Martín
Del aula a la PAU
2
Como llevamos manifestando a lo largo del libro, en las pruebas PAU de Asturias
utilizaremos el método de lápiz y papel, aunque en el aula podremos auxiliarnos de una
calculadora gráfica, en nuestro caso la CG 20 de CASIO, e incluso ir comprobando las posibles
respuestas aportadas.
Para S1 , al estar la superficie por debajo del eje OX, la expresión dará un valor negativo. Para
que quede positivo, cambiamos de signo la integral definida:
4
S1 → – ∫ 1 (x2 – 4x) dx
4
∫ 1 (x2 – 4x) dx
Aplicamos la Regla de Barrow
4
=[
=[
x3
– 2x2] 1 =
3
43
13
– 2·42] – [
– 2·12] =
3
3
64
1
=
– 32 –
+2=–9
3
3
S1 = 9 u2
S2 →
7
∫ 4 (x2 – 4x) dx
7
∫4
(x2 – 4x) dx =
Integrales. Aplicaciones
www.aulamatematica.com
3
Aplicamos la Regla de Barrow
7
x3
2
=[
– 2x ] 4 =
3
73
43
– 2·72] – [
– 2·42] =
3
3
343
64
=
– 98 –
+ 32 = 27
3
3
=[
S2 = 27 u2
St = S1 + S2
St = 9 u2 + 27 u2 = 36 u2
VISUALIZACIÓN Y CÁLCULO DIRECTO CON CALCULADORA GRÁFICA
Simplemente bastará con representar el valor absoluto de la función:
Una vez que conocemos la gráfica de la función, es sencillo comprobar los resultados
obtenidos si tenemos unos mínimos conocimientos teóricos matemáticos...
Comprobación directa con la
calculadora científica:
Criterios de corrección y calificación especificados en la prueba oficial:
(a) Calcular la primitiva: 0.75 puntos (b) Representar la función: 1. Calcular el área: 0.75 puntos.
 Abel Martín