DECISIONES BAJO RIESGO: MÉTODOS PROBABILÍSTICOS

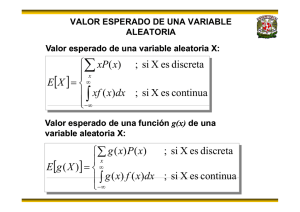
DECISIONES BAJO
RIESGO: MÉTODOS
PROBABILÍSTICOS
Escuela de la Ingeniería de la Organización
INTRODUCCIÓN
„
„
„
Por qué el uso de las probabilidades?
Para qué medir el riesgo?
Estadística Descriptiva
„
„
„
„
„
„
„
Medidas de tendencia central
Medidas de dispersión
Histogramas de frecuencias
Distribuciones de probabilidad
Estimación de parámetros
Métodos de pronóstico
Simulación Montecarlo.
PROBABILIDAD
„
Probabilidades Objetivas: Pueden concluirse a partir de una
serie de observaciones. Pueden ser:
A priori: Son aquellas que pueden ser computadas antes del
experimento, porque la naturaleza del evento que ocurrirá es
previamente reconocido.
Ej. Lanzar un dado y sacar el numero 2.
Ej2. Lanzar dos dados y sacar la suma 1 y 1.
Éstas deben poder ser conocidas sin un gran número de
experimentos ni grandes bases de datos.
… Empíricas: Son aquellas que se basan sobre grandes
cantidades de datos históricos, que permiten construir tablas de
frecuencias relativas de ocurrencia.
Ej. Probabilidades de incendios, accidentes, producción,
demandas de productos, muertes, etc.
…
PROBABILIDAD
„
Probabilidades
Subjetivas:
Son aquellas cuya
valoración se basa en la información histórica que
pudiese existir, ajustada por las creencias racionales de
un tomador de decisiones inteligente, que está
familiarizado con la naturaleza de la situación
La información histórica no es suficiente para usar el
concepto de probabilidades empíricas o de tablas de
frecuencia.
Ej. Cuál es la probabilidad de que al lanzar un nuevo
servicio financiero dirigido a estudiantes universitarios,
este producto sea muy demandado, medianamente
demandado o no tenga ninguna demanda? (existen
servicios similares, pero diferentes).
TOMA DE DECISIONES CON
PROBABILIDADES
„
-
-
Criterio de la Máxima Posibilidad:
Consiste en identificar el estado de la naturaleza más
probable (“A priori”), y luego seleccionar la alternativa
asociada al mayor pago: Ejemplo:
Qué ocurre con los pagos altos de alternativas
asociadas a eventos menos probables? (riesgo /
rentabilidad)
Qué ocurre si existen muchos eventos, y el evento más
probable, tiene por si mismo una baja probabilidad?
TOMA DE DECISIONES CON
PROBABILIDADES
„
-
Regla de decisión de Bayes:
Usando las mejores estimaciones disponibles de las
probabilidades de los estados de la naturaleza (A priori)
se calcula el valor esperado del pago de cada
alternativa. Se selecciona la alternativa asociada al
mayor valor esperado.
Qué precauciones debería tenerse con este método?
Probabilidad simple, condicional, conjunta y
marginal
„
„
„
„
Probabilidad simple: Es aquella que no está
condicionada a la ocurrencia de otro evento (Ej. P(a))
Probabilidad Condicional: Dado que otro evento ya
ocurrió, cuál es la probabilidad de que el evento ocurra?
(Ej. P(A/B))
Probabilidad Conjunta: Es la probabilidad de que ocurra
una serie de eventos de forma simultánea. (Ej. P(AB))
Probabilidad Marginal: Corresponde a la suma de las
probabilidades conjuntas para un evento, y corresponde
a una probabilidad simple. (Ej. Si el evento A puede
ocurrir con el evento B o sin el evento B, entonces
P(A) = P(A.B) + P(A. no B)
EJEMPLO 1
ACCIDENTES AUTOMOBILÍSTICOS
Suponga que se ha recolectado un largo número de datos de accidentes
automovilísticos en una cierta área geográfica, y que se ha clasificado la
información en accidente serios (si ocurrió una fatalidad) y no serios (si no
ocurrió una fatalidad). Suponga también que fue posible identificar si el
conductor había estado tomando bebidas alcohólicas justo antes del
accidente.
A partir de la anterior tabla, identifique las probabilidades marginales
(simples) conjuntas y condicionales.
Dependencia e Independencia Estadística
Si los eventos A y B son independientes, la ocurrencia de uno
de los eventos, no tendrá influencia ni proveerá de mayor
información acerca de la probabilidad de ocurrencia del otro
evento. Pero si los eventos son estadísticamente
dependientes, entonces la ocurrencia de uno de los eventos
afectará la probabilidad de ocurrencia del otro evento.
Si los eventos A y B son independientes, entonces:
P(A) = P(A/B)
P(B) = P(B/A)
La independencia o dependencia estadística, no deberá ser
confundida con relaciones de causa – efecto.
EJEMPLO 2
Composición de los asistentes a un seminario
Suponga que un seminario de administración contiene 50 estudiantes. 30 de
éstos son hombres. 40 tienen un grado en ingeniería y los demás un grado en
ciencias. Hay 6 científicos hombres.
A partir de los datos, identifique si existe o no, independencia estadística entre
el sexo de los asistentes y el tipo de grado que éstos tienen.
Construya la tabla de proporciones, y a partir de esta, compare la
probabilidad de que un asistente al seminario seleccionado aleatoriamente
sea un hombre, con la probabilidad de que este estudiante además sea
hombre dado que tiene estudios en ingeniería.
PROBABILIDAD: ALGUNAS RELACIONES
MATEMÁTICAS
COMPLEMENTACIÓN: La probabilidad marginal de que un evento ocurra o
no ocurra.
P(A) + P(Ā) = 1
MULTIPLICACIÓN: La probabilidad conjunta de que dos eventos
estadísticamente independientes ocurran simultáneamente.
P(AB) = P(A y B) = P(A) * P(B)
Y si no son estadísticamente independientes, entonces:
P(AB) = P(B) * P(A/B) = P(A) * P(B/A)
ADICIÓN: La probabilidad de que ocurra el evento A o el evento B (si son
mutuamente excluyentes).
P(A ó B) = P(A) + P(B)
Y si no son mutuamente excluyentes
P(A ó B) = P(A) +P(B) – P(AB)
TOMA DE DECISIONES CON EXPIREMENTACIÓN
„
„
Para mejorar las estimaciones preliminares de las probabilidades
cada uno de los estados de la naturaleza, es frecuente realizar
pruebas experimentales, que arrojen mayor información acerca
de la posibilidad de que ocurran los estados de la naturaleza,
según los resultados de las pruebas.
A partir de la información obtenida, realizamos los cálculo de las
probabilidades posteriores (“A posteriori”). Para esto, utilizamos
el análisis Bayesiano. Finalmente con esta información,
podremos encontrar los pagos esperados con información
muestral, y a su vez diseñar una estrategia óptima de decisión.
Miremos un ejemplo.
TEOREMA DE BAYES
„
„
„
„
n = número posible de estados de la naturaleza
P( Estado = estado i ) = Probabilidad a priori de que el estado de la
naturaleza verdadero, sea el estado i. (i = 1,2,3,…n)
Resultado j = Un valor posible del resultado de la prueba.
P( estado i / Resultado j ) = Probabilidad posterior de que el estado de
la naturaleza verdadero sea el estado i (i = 1,2,3,…n) , dado que el
resultado de la prueba fue el resultado j.
Si se conoce experimentalmente, las probabilidades
P( Resultado j / Estado i) y P( estado i), entonces:
¿CONTRATAR UN ESTUDIO ADICIONAL?
Valor de la experimentación (2 métodos)
•Valor esperado de la información perfecta (VEIP):
Este método, consiste en determinar el valor potencial de realizar un experimento
previo. En este caso se supone que la experimentación eliminará toda la
incertidumbre sobre cuál es el estado verdadero de la naturaleza.
Pago esperado con IP =∑(pago máximo del estado i)*P(estado i) para todo estado i.
VEIP = pago esperado con información perfecta – pago esperado sin
experimentación (Regla de Bayes)
•Valor esperado de la experimentación (VEE):
Consiste en involucrar los pagos esperados según los resultados de la
experimentación
VEE = Pago esperado con experimentación – Pago esperado sin experimentación,
donde:
Pago esperado con experimentación = ∑P(resultado j)*E(pago*/resultado j)
•Deberán tomarse los pagos SIN costos de experimentación.
EJEMPLO 3: PROYECTO DE CAPITAL DE RIESGO
Los proyectos de capital de riesgo tienen como objetivo fomentar industrias
particulares que implican un alto riesgo para el inversionista acerca de los
resultados, y a su vez estados de la naturaleza con retornos muy atractivos.
Un compañía administradora de inversiones, tiene la posibilidad de invertir en un
proyecto de capital semilla. Después de realizar un análisis, se enfrenta a la
siguiente situación:
Inicialmente, realice un árbol de decisión para representar los pagos, los
estados de la naturaleza y las decisiones. (continua …)
EJEMPLO 3: EL ÁRBOL DE DECISÓN SIN EXPERIMENTACIÓN
PAGOS TOTALES (S1)
CONSERVADOR (d1)
2
PAGOS TOTALES (S1)
1
MODERADO (d2)
3
PAGOS PARCIALES (S2)
PAGOS TOTALES (S1)
AGRESIVO (d3)
4
8
PAGOS PARCIALES (S2)
PAGOS PARCIALES (S2)
4
14
1
30
-10
Los cuadros son utilizados como nodos de decisión.
Los círculos son utilizados como nodos de probabilidad.
Las ramas son utilizadas para nombrar las decisiones y los resultados.
El primer paso para resolver un problema complejo es descomponerlo en una
serie de subproblemas más pequeños. Los árboles de decisión facilitan la
construcción de una estrategia para enfrentar un problema de toma de
decisiones en un contexto probabilístico.
TOMA DE DECISIONES CON EXPERIMENTACIÓN
EJEMPLO 3:
Suponga que una firma consultora ofrece una serie de pruebas e
investigaciones económicas, que pronostique si los resultados del proyecto
del capital semilla serán o no satisfactorios.
Igualmente, esta firma nos indica que con base en su experiencia los
resultados de las pruebas que han realizado son :
P(Resultado = Favorable/ Estado = Pagos Totales) = 0.9
P(Resultado = Favorable / Estado = Pagos Parciales) = 0.25
El costo del estudio es de 3 millones de USD.
Diseñe una estrategia óptima de decisión, y calcule el valor máximo que usted
pagaría por el informe de la firma consultora.
TOMA DE DECISIONES CON EXPERIMENTACIÓN
EJEMPLO 3: ARBOL DE DECISIÓN
Una forma de representar las decisiones y los posibles pagos, sería la
siguiente.
Calcule las probabilidades “A posteriori”, y desarrolle el árbol de decisión de
derecha a izquierda. Concluya a cerca de las decisiones a tomar.
VARIABLES ALEATORIAS
EXPERIMENTO:
Es un procedimiento estable, que puede reproducirse repetitivamente. El riesgo
se presenta en éste, pues cada que se genera el proceso, los resultados no
necesariamente son los mismos.
VARIABLE ALEATORIA:
Es la “regla” que se usará para la asignación numérica de cada uno de los
eventos posibles. Cada uno de los valores que toma la variable aleatoria,
corresponde a uno de los posibles eventos del experimento.
Ejemplos: Número de pasajeros en un vuelo. – Sexo de un estudiante (Hombre
o Mujer) – Productos vendidos por hora – etc.
VARIABLES DISCRETAS Vs. VARIABLES CONTINUAS:
Para una variable aleatoria discreta, es posible identificar el número de
eventos posibles, en un rango particular. Una variable aleatoria continua, puede
tomar infinitos valores en un rango específico.
Para cada una de las variables aleatorias se deberá definir su función de
probabilidad.
MEDICIÓN DE RIESGO
• EVALUACIÓN DE CRITERIOS ECONÓMICOS:
Los indicadores económicos de cada uno de los métodos, serán evaluados a través
de medidas estadísticas de tendencia central y de dispersión. Por ejemplo, para
identificar la bondad del indicador, usaremos el valor esperado. (Ej. VPN, TIR, etc.)
N
X=
∑X
i
N
i =1
ó
N
X = ∑ Xi . Pi
i =1
Para identificar la dispersión del indicador económico (Ej. los flujos, el VPN, etc),
utilizaremos la varianza y la desviación estándar.
2
N
VAR(X) =
∑[Xi - X]
i =1
N
ó VAR(X) =
N
2
∑[Xi - X] . Pi
i =1
El coeficiente de variación también lo utilizaremos para comparar la bondad de
diferentes alternativas. Mide la dispersión relativa de los datos en relación a la
media:
CV=
σ
X
Regrese al ejercicio de la Planta de
juguetes, y conteste la pregunta 2.
GENERACIÓN DE NÚMEROS ALEATORIOS
•Para la generación de números aleatorios en excel, es posible utilizar varios métodos:
•Generados de número aleatorios: Herramientas – análisis de datos – generación
de números aleatiorios. Por este método, los números aleatorios son generados
como valores (Debe estar activado el complemento Herramientas para análisis).
Otra posibilidad, es generar el número aleatorio directamente desde la hoja de
cálculo con las funciones:
= Aleatorio() Genera números aleatorios provenientes de una distribución uniforme
entre 0 y 1
= Aleatorio. Entre (inferior;Superior) Genera números aleatorios de una distribución
uniforme entre los valores especificados
HERRAMIENTAS DE ANÁLISIS DE UNA SERIE
RESUMEN ESTADÍSTICO DE UNA SERIE:
En excel es posible realizar un análisis de una serie de datos, a través de la estadística
descriptiva.
Cada uno de estos valores también pueden ser calculados a través de las funciones de
hoja de cálculo. Realice el ejericio, para verificar sus resultados.
HISTOGRAMA
En el menú de Análisis de Datos, también se encuentra disponible la construcción de un
Histograma. Esta herramienta es útil para asociar la distribución de una serie de datos
con una función de distribución conocida.
80
Frecuencia
70
60
Frecuencia
Histograma
50
40
30
20
10
.3
9
-2
-2
.7
6
94
4
77
47
6
- 2 209
.0
22 898
97
-1 204
.6
9
49
-1
73
.2
42
76
- 0 496
.9
03 351
-0 258
.5
30 502
- 0 020
.1
56 653
78
0.
28
21
04
64
5
0.
58 504
5
96
92
0.
89
96
4
29
30
1.
7
33
61 43
68
1.
5
70
94 92
06
2.
08 441
26
2.
44
45
29
58
82
2.
13
82
9
91
19
98
7
0
Clase
Esto también se puede realizar
directamente en la hoja de cálculo, a
través de la función FRECUENCIA en
forma matricial.
DISTRIBUCIÓN DE PROBABILIDAD EMPÍRICA
DISCRETA
Consiste en construir la función de densidad y la función de distribución
acumulada, a partir del conjunto de datos con que se cuenta.
Se recomienda esta distribución cuando la variable aleatoria no se ajuste a
una distribución de probabilidad, y/o cuando la variable aleatoria toma un
número muy limitado de valores discretos.
Con el fin de simular el comportamiento de la variable aleatoria, se realiza lo
siguiente:
1. Se establece en qué rango de probabilidades se encontraría un número
aleatorio generado (función de distribución acumulada)
2. Se genera un numero aleatorio. Este número aleatorio corresponde a un
valor de la distribución acumulada.
3. Se identifica cuál es el valor de la variable aleatoria, que le corresponde a
la probabilidad simulada.
4. Se repite el proceso.
EJEMPLO 3:
DISTRIBUCIÓN DE PROBABILIDAD EMPÍRICA DISCRETA
Se estima que la vida útil de un proyecto de inversión (carretera nacional)
puede ser de 3, 5, 7 o 10 años, con las siguientes probabilidades
respectivamente: 20%, 40%, 25%, 15%.
Construya para esta variable:
1. La función de densidad (grafique)
2. La función de probabilidad acumulada (grafique)
3. Encuentre la Media y la Desviación Estándar de la variable aleatoria.
4. Genere un proceso de simulación sobre la variable y genere un histograma
de frecuencia sobre los datos obtenidos.
RECOMENDACIÓN:
Utilizar el generador de números aleatorios de Excel.
Utilice la función BUSCARV para encontrar los valores simulados de la V.A.
EJEMPLO 4:
THE NEWSPERSON PROBLEM
Se necesita determinar cuántos Calendarios del año 2006 ordenar desde este
mes. El costo es de $2 USD por calendario, el precio de venta es de $4.50
USD. Después del 1º de Enero, los calendarios que no se vendan son
reintegrados por $0.75 USD. La mejor estimación de la demanda de los
calendarios, sigue las siguientes probabilidades:
Cuántos calendarios deberían ordenarse?
Para el análisis realice una simulación montecarlo para cada una de las
posibles decisiones. Calcule, el promedio de los ingresos netos en cada
decisión, la desviación estándar, y el coeficiente de variación.
INTERVALO DE CONFIANZA
600
500
400
300
200
100
0
125
312.5
500
Para cada una de las series simuladas es
posible calcular un valor de la media. Sin
embargo, se puede considerar éste como
un valor apropiado?
FRECUENCIA
PROMEDIO
Si se realiza un nuevo proceso de simulación se obtendrá nuevos valores para la media, por
lo que no es posible conocer con exactitud el valor de la media desde ninguna simulación.
Así pues qué tan apropiado es la estimación de la media?
Solo se puede estar un 95% seguro de que el promedio de la media estará entre:
PROMEDIO ± 2 * DESVIACION ESTANDAR / RAIZ (nº iteraciones)
Si se desea determinado nivel de precisión en la estmación de la media, entonces se deberá
despejar el número de iteraciones así:
2 * DESVIACIÒN ESTÁNDAR / RAIZ (nº iteraciones) = márgen deseado del intervalo de
confianza.
DISTRIBUCIÓN BINOMINAL
La variable aleatoria (x) representa el número de éxitos en un numero fijo (n) de intentos,
experimentos de Bernulli. La probabilidad de estos resultados en cada ensayo es
constante y los ensayos son independientes.
1. La variable aleatoria solo puede tomar 2 posibles valores (Éxito ó Fracaso)
2. La probabilidad de los posibles resultados, permanece constante de un experimento
a otro.
3. En la secuencia de experimentos, los resultados de uno de ellos no tiene efecto
sobre el resultado de algún otro.
Probabilidad de éxito (P), probabilidad de fracaso q=(1-P):
n
n-x
p(x) =   p x (1 - p )
x
 
µ = n.p
si x = 1,2,......, n
y
σ = n.p.q
EJEMPLO: Se conoce que en una gran ciudad, el 25% de la población está subscrita al
periódico local. Una muestra de 20 habitantes es seleccionada aleatoriamente. Cuál es la
probabilidad de que 2 o menos de las personas seleccionadas estén subscritas al
periódico?, cuál es la probabilidad de que más de dos y hasta 5 personas estén inscritas?
NOTA: La distribución binomial requiere del supuesto de “muestreo con reemplazo”.
En Excel puede usarse la función =DISTR.BINOM
DISTRIBUCIÓN HIPERGEOMÉTRICA
A diferencia de la distribución binomial, en esta distribución el muestreo es
llevado a cabo sin reemplazo.
Esta distribución describe la probabilidad de encontrar x exitos en una muestra
aleatoria de tamaño n, que se selecciona sin reemplazo de una población
N, en donde se sabe que K resultados de la población N son éxitos, y N - K
fracasos.
E(x) = np
V(x) =n.p.q.(N-p)\(N-1)
EJEMPLO: Un lote de 40 componentes electrónicos se considera aceptable,
sino contiene más de 3 componentes defectuosos. Actualmente se usa un
procedimiento de muestreo del lote, tal que se seleccionan 5 componentes
y se rechaza el lote si se encuentra uno defectuoso.
Cuál es la probabilidad de que exactamente 1 componente defectuoso se
encuentre en la muestra si se conoce que existen 3 defectuosos en todo el
lote?
EN EXCEL PUEDE USARSE LA FUNCIÓN DISTR.HIPERGEOM
DISTRIBUCIÓN POISSON
La distribución de Poisson describe el número de veces “x” que un evento
ocurre en un intervalo de tiempo dado. Por ejemplo, el ritmo promedio al
que llegan los vehículos a un peaje, demanda promedio de un articulo en
un almacén, etc.
Caracterizado por un valor “lambda” igual a el número de ocurrencias por
unidad de tiempo (media).
P(x ) =
λx e − λ
x!
x = 1,2,...
Media = Varianza = lambda * t
A diferencia de la distribución binomial, en este caso no se conoce la
proporción de éxitos en la población, y además no se tiene un n definido.
EJEMPLO: Suponga que el paso de vehículos por un peaje, se ajusta a
una distribución de Poisson, y que en promedio pasan 200 carros por
hora. Cuál es la probabilidad de que no pase un carro en el próximo
minuto?
EN EXCEL PUEDE USARSE LA FUNCIÓN POISSON
DISTRIBUCIÓN NORMAL
Describe muchos fenómenos aleatorios que ocurren
en la vida diaria.
Es simétrica y su media es igual a la mediana.
El Rango de “x” no esta limitado pero los valores se
centran alrededor de la media.
e − (x − µ )
2
f (x) =
/ 2σ
2Π σ
N
σ (X) =
∑ [X
i=1
N
i -
2
-∞ < x < ∞
2
µ
]
2
N
µ =
∑
Xi
i=1
N
Distribución Normal Estándar
Z=
X - X
σ
Distribución Normal Estándar
µ =0
σ =1
…
Probabilidades normales
seleccionados de Z
para
valores
Distribución Lognormal
Se usa en situaciones donde los valores se sesgan
positivamente. Por ejemplo precios de acciones,
valuación de seguros, etc.
… La variable incierta puede incrementarse sin limite
pero no puede caer por debajo de cero.
… La variable se sesga positivamente pero la mayoría
de valores se encuentran cerca al limite inferior.
… El Ln de la variable incierta produce una distribución
normal.
En Excel pueden usarse las funciones:
DISTR.LOG.INV y la función DISTR.LOG.NORM
…
Distribución Triangular
…
…
…
La distribución triangular no puede generarse con una
función especifica de Excel, sin embargo puede
programarse utilizando la función de densidad y la función
acumulativa de la distribución.
Distribución basada en una posición pesimista, probable y
optimista.
La distribución esta definida por tres parámetros: valor
mínimo (a), Valor probable (b), valor máximo (c). Variando
el parámetro mas probable la distribución puede ser
simétrica o asimétrica.
Parámetros:
P(x)
h
a
b
c
1
µ = (a + b + c)
3
1 2 2 2
σ=
a + b + c − ab- ac- bc
18
(
)
Distribución Triangular
…
La función de densidad define la
probabilidad de ocurrencia de cada valor x.
Función de Densidad
f(x)
2 (x - a)
a ≤ x≤ b
(c- a)(b- a)
- 2 (x - c)
b ≤ x≤ c
(c- a)(c- b)
f(x)=
h
A1
A2
a
c
b
Distribución Triangular
…
La Función Acumulativa define
probabilidad acumulada hasta el valor x
Función Acumulativa
F(x)=
(x - a)2
(c- a)(b- a)
2
1-
la
F(x)
a ≤ x≤ b
(c- x)
b ≤ x≤c
(c- a)(c- b)
1
R
a
xb
c
Distribución Triangular
Es utilizada cuando hay información incompleta de la
variable o como aproximación a otras distribuciones.
El resultado simulado se basa en:
…
…
… Generación del numero aleatorio R y este será igual a F(x)
…
…
(Valor entre
0-1)
Comparar R con A1 (probabilidad acumulada entre a – b) y determinar si
es mayor o menor.
Calcular el valor (x) de la función acumulativa dependiendo si R es
mayor o menor que A1.
p(x)
2
b-a
,
A1 =
c-a
c-a
si R < A1 ∴ x = a + R.(c - a).(b - a)
h=
h
A1
A2
si R > A1 ∴ x = c - (1 - R).(c - a).(c - b)
a
b
c
Distribución Uniforme
…
…
…
La variable aleatoria se mueve entre un valor mínimo y
máximo todas con igual nivel de probabilidad .
Se usa frecuentemente cuando hay poco conocimiento de
la variable.
(b- a)2
a +b
y σ=
Parámetros: µ =
2
12
1
a ≤x≤b
b-a
x -a
a ≤x≤b
Funcion Acumulativa : F(x) =
b-a
Funciónde probabilidad : f(x) =
p(c < x < d) =
d-c
b-a
f(x)
a
c
d
b
Distribución Exponencial
Se usa para describir eventos que ocurren
aleatoriamente en el tiempo.
… Describe la cantidad de tiempo entre ocurrencias.
… La distribución no se afecta por eventos previos.
En Excel puede usarse la función
DISTR.EXP
…
TEOREMA DE LIMITE CENTRAL
„
„
„
El Teorema del Límite Central indica que, bajo condiciones muy generales,
la distribución de la suma de variables aleatorias tiende a una distribución
gaussiana cuando la cantidad de variables es muy grande.
Si se está realizando el muestreo de una población con distribución
desconocida, sea finita o infinita, la distribución muestral de ẍ será
aproximadamente normal con media µ y varianza σ2/n dado que el tamaño
de la muestra es grande.
Teorema:
Si ẍ es la media de una muestra aleatoria de tamaño n, que se toma de una
población con media µ y varianza finita σ2, entonces la forma del límite de la
distribución de
se distribuye aproximadamente como una variable,
o de manera equivalente,
TEOREMA DE CHEBYSHEV
„
„
El matemático Ruso P.L. Chebyshev descubrió que la
fracción del área entre cualquiera de dos valores
simétricos alrededor de la media, se relaciona con la
desviación estándar.
La probabilidad de que cualquier variable aleatoria X,
asuma un valor dentro de k desviaciones estándar de la
media, es al menos 1-1/k2 . O sea:
P(µ-kσ < X < µ+kσ ) ≥ 1 – 1/k2
Ejemplo:
Suponga que el VPN de un proyecto tiene media µ = 8’ y varianza
σ2=9’, y una distribución de probabilidad desconocida.
Encuentre:
a) P(-4’ < VPN < 20’)
b)P(abs(VPN-8)≥6)
PRUEBAS DE BONDAD DE AJUSTE
Prueba de Normalidad: Jarque Bera
Esta prueba se basa en la curtosis y la simetría de la muestra. S
representa el coeficiente de asimetría, k-3 es el excedente de
curtosis y n el tamaño de la muestra.
H0: Los datos se distribuyen normalmente
H1: Los datos no se distribuyen normalmente.
α: Nivel de Significancia de la prueba.
Estadístico de prueba:
La prueba se rechaza a un nivel de confianza de 1-α si JB >= X2(2,α).
Recuerde que la curtosis de una distribución normal es 3.
Ejemplo: Realice una prueba de normalidad sobre la serie de números
aleatorio normales generada con anterioridad. En Excel puede usar la
función PRUEBA.CHI.INV. Utilice un n grande.
PRUEBAS DE BONDAD DE AJUSTE
Chi cuadrado
Esta prueba aplica solo sobre distribuciones de probabilidad discretas
como la Poisson o la binomial (distribuciones univariadas). También
puede aplicarse también sobre muestras continuas agrupadas en
clases.
Los datos deben organizarse en k clases ascendentes. Esta prueba no es
precisa si en alguna clase existe una frecuencia observada o esperada
menor al 5%.
Definición de la prueba:
Oi :Es la frecuencia observada para la clase i
Ei :Es la frecuencia esperada en la clase i.
H0: Los datos siguen una distribución específica dada
H1: Los datos no siguen una distribución específica.
Estadístico de prueba:
PRUEBAS DE BONDAD DE AJUSTE
Chi cuadrado
Donde Oi es la frecuencia observada para la clase i y Ei es la frecuencia esperada
en la clase i. La frecuencia esperada se calcula como:
F, es la función de probabilidad acumulada de los datos que se desean probar, Yu
es el límite superior de la clase i, YL es el límite inferior de la clase i, N es el total de
las observaciones.
Ejemplos Iniciales de Simulación Montecarlo
1.Estimación del número pi.
2. Swap DTF – IPC
3.The Hippo Example