TÉCNICAS DE FILTRADO ÓPTICO PARA ANÁLISIS DE FRACTALES

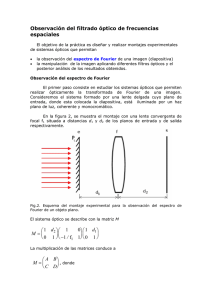
TÉCNICAS DE FILTRADO ÓPTICO PARA ANÁLISIS DE FRACTALES
J. A. Rodrigo Martín-Romo y D. Rodríguez Merlo
Departamento de Óptica, Facultad de Ciencias Físicas, Universidad Complutense de Madrid,
28040 Madrid
1. Introducción
A continuación proponemos diversas técnicas de filtrado óptico espacial para analizar la
información que contienen los objetos fractales. En particular analizaremos dos estructuras
fractales regulares Cantor Bars y el fractal de Vicsek, ambas de nivel n=4. Para ello
emplearemos un sistema óptico 4-f, que permite realizar operaciones de filtrado y
reconstrucción. A partir de este estudio experimental veremos que los espectros de Fourier
asociados a estos objetos tienen una estructura cuasi-periódica. Finalmente, compararemos
estos resultados experimentales con los obtenidos a partir de la simulación numérica por
ordenador de este proceso de filtrado y reconstrucción.
2. Descripción del sistema óptico 4-f
El sistema óptico 4-f empleado consta de los siguientes elementos
Figura 1. Sistema óptico 4- f. La longitud de onda del láser He-Ne utilizado es 632.8 nm, y potencia de 20mW.
La disposición del filtro espacial y de la lente colimadora L permite obtener una
iluminación uniforme sobre el plano Objeto, mientras que los polarizadores permiten regular
la intensidad del haz. Las lentes convergentes L1 y L2 tienen distancias focales f1 =50 cm y
f2 =18 cm respectivamente. Nótese que ambas lentes presentan aberraciones, si bien la lente
L1 es una lente de Fourier corregida.
Este es un sistema óptico típico para realizar operaciones de filtrado óptico de
imágenes, en nuestro caso se filtra el espectro de Fourier del objeto correspondiente por
medio de una rendija rectangular contenida en el plano de Fourier del sistema. De esta forma
podemos estudiar, la estructura e información que contiene el espectro de Fourier de estos
objetos fractales particulares.
2. Procesos de filtrado óptico espacial
Los objetos fractales Cantor Bars y fractal de Vicsek, empleados en los procesos de
filtrado y sus correspondientes espectros de Fourier, son los siguientes
(a)
(b)
(c)
(d)
Figura 2 Cantor Bars (a) y el fractal de Vicsek (b), junto con sus respectivos espectros de Fourier (c) y (d).
En este caso el proceso de filtrado consiste en desplazar una rendija rectangular
transversalmente a lo largo del eje X (Fig.1) manteniendo su anchura w=1.2 mm constante
durante el desplazamiento. El rango de desplazamiento es 0 <d<1.0 mm. La rendija en todo
momento está contenida en el plano de Fourier y es perpendicular al eje X. La posición inicial
de la rendija coincide con la posición del máximo central del espectro de Fourier, el
desplazamiento se realiza sólo en un sentido puesto que los espectros son simétricos. Este
desplazamiento se efectúa a intervalos regulares del orden de décimas de milímetro. La
secuencia de imágenes obtenida es la siguiente
(a)
(b)
(c)
(d)
(e)
Figura 3. Secuencia de imágenes obtenidas a través del filtrado desplazando la rendija. La imagen (a) es el
objeto estudiado y el resto de imágenes (b, c, d, e) corresponden consecutivamente a posiciones d crecientes, en
el rango 0 <d<1.0 mm.
Se aprecia que para las posiciones (a) d=0 mm y (d) d=0.8 mm tenemos dos imágenes
muy similares (del mismo nivel fractal) lo que indica claramente una periodicidad. Entre estas
posiciones el nivel fractal del objeto reconstruido es menor que el del objeto (de nivel cuatro).
Este hecho está justificado teóricamente a partir de la distribución de intensidad del espectro
de Fourier, ya que para el conjunto de Cantor Bars de nivel n esta intensidad es:
2
 n −1
  sin(πq ) 
I n (q ) = 2 ∏ cos( 2πm i q ) 

 i =0
  πq 
2n
2
(1)
donde m = 2.8 (en este caso) es el factor de escala y q es la frecuencia espacial [1]. La cuasiperiodicidad se explica entonces a través del factor de estructura dado por el producto de las
funciones coseno, la función sinc representa el factor de modulación de la intensidad.
En el caso del fractal de Vicsek también se observa una cuasi-periodicidad, tal y como
se puede apreciar en la Fig. 4.
Figura 4. La secuencia está ordenada de izquierda a derecha según el desplazamiento (creciente) de la rendija.
El desplazamiento es del orden de décimas de milímetro en cada paso, en el rango 0 <d<1.0 mm.
Otro proceso de filtrado consiste en fijar la posición de la rendija y disminuir
progresivamente su anchura de tal manera que siempre esté centrada con respecto a la
posición del máximo central del espectro de Fourier. En el caso del fractal Cantor Bars se
obtiene la siguiente secuencia de imágenes
.
(a)
(b)
(c)
Figura 5. Secuencia de imágenes correspondiente al filtrado con anchuras w de la rendija dadas en (a), (b) y (c),
respectivamente.
Por tanto, a partir del filtrado del espectro de Fourier se puede determinar rasgos de su
estructura como la cuasi-periodicidad. De estos procesos de filtrado se obtienen
reconstrucciones del objeto con un nivel fractal inferior, de lo que se infiere que determinadas
secciones del espectro contienen información de todo el objeto fractal. Este hecho parece ser
una manifestación de una de las propiedades que caracterizan a los fractales, a saber, la
invarianza bajo cambios de escala.
5. Comparación entre resultados experimentales y la simulación numérica
Estos procesos de filtrado, anteriormente descritos, pueden simularse realizando la
transformada de Fourier discreta, DFT, de la correspondiente región del espectro de Fourier
del objeto. Esta simulación numérica constituye una comprobación teórica de los procesos de
filtrado realizados. Tal y como se aprecia en Fig.5 existe un buen acuerdo entre la simulación
y las imágenes experimentales mostradas en las figuras 3, 4 y 5.
(a)
(b)
(c)
(d)
Figura 5. Imágenes obtenidas a través de la simulación numérica del filtrado, para los dos objetos fractales
estudiados Cantor Bars (a y b) y fractal de Vicsek (c y d). Las imágenes (a, c y d) corresponden al primer
proceso de filtrado y la imagen (b) corresponde al segundo proceso de filtrado, ambos descritos anteriormente.
Bibliografía
[1] C. Allain, M. Cloitre, Phys. Rev. B, 33 (1986), 3566.
[2] Y. Sakurada, J. Uozumi, T. Asakura, Pure Appl. Opt. 3 (1994) 371.
Agradecimientos
Financiado por el Rectorado de la UCM (Proyecto PIE 2002/1) y realizado en colaboración
con M.L. Calvo y T. Alieva.