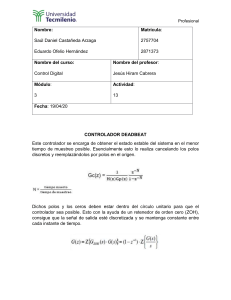
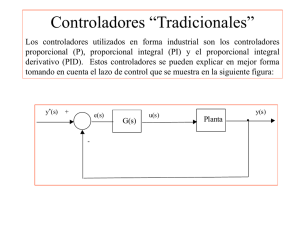
K 1s )]s(G[)s(G + ν = = 1s 1 )s(F + α = )1s(K 1s )s(G)s(F)s(Q + α + ν

15.3 Síntesis de PID usando la parametrización
Modelos de primer orden
Ko
K o , νo  0
ν os  1
Como no hay ceros inestables, el modelo es invertible exactamente,
luego:
 s1
G oi (s)  [G o (s)] 1  o
Ko
Para que Q(s) sea bipropio; FQ(s) debe tener grado relativo 1, por
ejemplo:
1
FQ (s) 
s  1
Por lo tanto:
 os  1
Q(s)  FQ (s)G oi (s) 
K o (s  1)
Y el controlador es:
Consideremos el modelo G o (s) 
C(s) 
 s1

Q(s)
1
 o
 o 
1  Q(s)G o (s) K o s K o  K o s
Que resulta ser un PI con:
KP 
o
K o
KI 
1
K o
Luego tenemos que:
To (s)  Q(s)G o (s)  FQ (s)G oi (s)G o (s)  FQ (s) 
1
s  1
Donde  es el parámetro a sintonizar. Escogiendo  pequeño
hacemos el lazo más rápido. Con este controlador, las perturbaciones
son rechazadas por la función de sensibilidad nominal:
s
So (s)  1  To (s)  1  FQ (s) 
s  1
Valores pequeños para  rechaza la perturbación de salida más rápido
que con valores grandes de  . También  no se puede escoger
arbitrariamente pequeño debido a consideraciones de limitaciones en
el actuador.
Sistemas con retardos temporales.
Consideremos que el modelo nominal de una planta con retardo es:
G o (s)  e  s G o (s)
Donde G o (s) es la función de transferencia racional del sistema. La
sensibilidad nominal complementaria es:
 sτ
To (s)  e G o (s)Q(s)
Luego Q(s) se debe diseñar considerando la parte racional del modelo,
G o (s) , ya que el retardo no se puede invertir. Luego se necesita una
inversa aproximada de G o (s) (estable, causal y propia).
Si usamos el esquema realimentado para generar una inversa
estable, considerando que:
Q(s) 
C(s)
1  C(s)G o (s)
Cuando C( jw ) es grande, entonces Q( jw)  [G o ( jw)]1
Esto lleva al siguiente esquema:
Di(s)
R(s)
+
U(s)
C(s)
Do(s)
+
+
+
Planta
Y(s)
+
Dm(s)
+
(e  s  1)G o (s)
+
Ym(s) +
-
Es la forma tradicional del controlador de Smith.
En el caso de considerar la configuración usando la parametrización
Q(s), tenemos la figura que se muestra a continuación que es
equivalente al controlador de Smith.
Di(s)
R(s)
+
U(s)
Q(s)
Do(s)
+
+
+
Y(s)
+
Planta
Dm(s)
+
Ym(s) +
-
 s
e G o (s )
Forma Q(s) del controlador de Smith
Ejemplo:
Considere una planta con el modelo nominal dado por:
G (s )  e
s
2s  1
Diseñar un controlador que permita un buen seguimiento de la
referencia en un rango [0;1][rad/s].
Desarrollo: Usando la parte racional de Go(s) tenemos que:
Q(s)  FQ (s)G oi (s) 
( 2s  1)
(s 2  1,3s  1)
Lo cual da:
s
T(s)  Q(s)G(s)  FQ (s)G (s)G o (s) 
i
o
+
e
(s 2  1,3s  1)