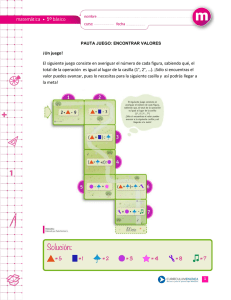
Invariantes y Problemas de Olimpiadas

Invariantes y Problemas de Olimpiadas
José Heber Nieto Said ([email protected])
Universidad del Zulia, Maracaibo, Venezuela.
Resumen
Un invariante es una función I, cuyo dominio es el conjunto de los estados de un sistema, tal que si existe una
transición válida del estado E1 al etado E2 , entonces I(E1 ) = I(E2 ). En este artículo se analizan varios ejemplos
que muestran la utilidad de este concepto para la resolución de problemas matemáticos de tipo olímpico.
Palabras y frases clave: invariante, sistema, olimpiadas matemáticas, resolución de problemas.
1.
Introducción
Un sistema es un conjunto de elementos interrelacionados, que forman un todo complejo y organizado. Vivimos
rodeados de sistemas: el universo, la Tierra, un océano, cada ser vivo, una célula, un átomo son ejemplos de sistemas.
Un sistema está en cada momento en un estado determinado, que suele ser descripto mediante los valores de ciertos
parámetros. Por ejemplo, un gas puede ser descripto especificando el volumen V que ocupa, su presión P , su temperatura T y su masa. Los sistemas son por lo general dinámicos, su estado cambia con el tiempo. ¿Cómo se puede,
entonces, alcanzar algún conocimiento sobre ellos? Bueno, una de las formas en que la ciencia lo logra es buscando
características que se mantengan invariables a lo largo del tiempo, generalmente bajo la forma de relaciones entre
los parámetros. A esas características se les llama invariantes del sistema. En el ejemplo del gas, una conocida ley
física dice que P V = nRT (donde n es la masa en moles y R una constante). Esta ley puede expresarse diciendo que
P V /(nT ) es un invariante.
En lo que sigue consideraremos sistemas discretos, en los cuales el conjunto de estados posibles E = {E1 , E2 , E3 , . . . }
es finito o numerable y el tiempo no es continuo, sino más bien una sucesión de instantes. En cada instante hay un
conjunto de transiciones válidas Ei → Ej que representan los cambios de estado posibles. Un juego como el ajedrez
es un buen ejemplo: un estado queda determinado por la posición de las fichas en el tablero, a quien le toca jugar y
alguna información adicional sobre las jugadas previas. Las transiciones válidas corresponden a las jugadas posibles
en cada estado, según las reglas del juego.
Se dice que un estado B es accesible desde otro estado A si existen una o más transiciones válidas que lleven el
sistema desde A hasta B, es decir si existe un conjunto de estados A = E0 , E1 ,. . . , En−1 , En = B y transiciones
válidas E0 → E1 , E1 → E2 ,. . . , En−1 → En .
Un problema típico es el de saber si un estado B es accesible o no desde otro estado A. Para probar que lo es,
basta hallar una sucesión de transiciones que nos lleve de A a B. Pero probar la inaccesibilidad suele ser más difícil.
Un enfoque exhaustivo (examinar todas las sucesiones de transiciones posibles) puede ser prohibitivo por el tiempo
requerido. En estos casos suele ser útil la noción de invariante, que definiremos como una función I : E → X, donde
E es el conjunto de estados del sistema y X un conjunto cualquiera, tal que para cada transición válida E1 → E2
se cumple I(E1 ) = I(E2 ). Si I es un invariante y B es accesible desde A, entonces por transitividad I(A) = I(B).
Por lo tanto si I(A) 6= I(B) entonces B no es accesible desde A (ni A desde B). Lamentablemente, de la igualdad
I(A) = I(B) no se puede deducir, en general, la accesibilidad.
2.
Algunos ejemplos sencillos
Ejemplo 1. Suponga que en una pizarra se escriben los números naturales del 1 al 100. A continuación se escogen
dos de esos números a y b, se borran y se escribe en la pizarra el valor de la suma a + b. Se continúa de este modo
hasta que quede un sólo número en la pizarra. ¿Cuál es ese número?
1
Solución. Un análisis exhaustivo no es viable, porque el número de maneras diferentes en que puede desarrollarse este
sistema es enorme. Pero tratemos de hallar un invariante. Si se borran a y b y se escribe en la pizarra a + b, habrá un
número menos en la pizarra, pero ¿hay algo que no haya cambiado? Sí, la suma S de todos los números en la pizarra.
Como al principio S = 1 + 2 + 3 + · · · + 100 = 5050, al final debe tener ese mismo valor y el número que queda en la
pizarra es siempre el 5050.
Ejemplo 2. Los números 1, 2, . . . , 20 se escriben en una pizarra. En una operación se borran dos números a y b y se
escribe el número a + b − 1. ¿Qué número queda en la pizarra después de 19 operaciones?
Solución. La suma S de los números que están en la pizarra no es un invariante, pues en cada operación disminuye en
1. Pero la cantidad N de números escritos también disminuye en 1, luego la diferencia D = S − N es un invariante.
El valor inicial de D es 1 + 2 + · · · + 20 − 20 = 1 + 2 + · · · + 19 = 190. Cuando quede solo un número x se tendrá
D = x − 1 = 190, por lo tanto el último número que queda en la pizarra es el 191.
Ejemplo 3. Los números 1, 2, . . . , 20 se escriben en una pizarra y se permite la siguiente operación: se borran dos
números a y b y se escribe el número ab + a + b. ¿Qué número queda después de realizar 19 de estas operaciones?
Solución. Notemos que ab + a + b = (a + 1)(b + 1) − 1. Si en una operación posterior se elige este número con algún
otro número c, se deberá escribir el número (a + 1)(b + 1)(c + 1) − 1. Esto sugiere que pensemos en el producto de los
números que están en la pizarra incrementados en 1, el cual evidentemente es un invariante. Inicialmente ese invariante
vale (1 + 1)(2 + 1) · · · (20 + 1) = 21!. Luego de 19 operaciones quedará un número x tal que x + 1 = 21!, por lo tanto
x = 21! − 1.
Ejemplo 4. En una pizarra están escritos los números naturales del 1 al 100. Jorge escoge dos de esos números a y b,
los borra y luego escribe alguno de los números a − b, b − a ó a + b. Continúa de esa manera hasta que queda un sólo
número k en la pizarra. ¿Puede determinarse la paridad de k?
Solución. En este caso el valor de k no queda determinado como en el ejemplo anterior; su valor depende de las
decisiones que se vayan tomando en el proceso. Más precisamente, si luego de borrar a y b Jorge escribe a + b, entonces
la suma no varía, pero si escribe a − b la variación de la suma es a − b − (a + b) = −2b, y si escribe b − a la variación
es b − a − (a + b) = −2a. Se ve entonces que la variación de la suma es siempre un número par (0, −2b ó −2a). Por lo
tanto la paridad de la suma es un invariante. Como inicialmente la suma es par (ya que es 5050), seguirá siendo par
hasta el final y por lo tanto k debe ser par.
Ejemplo 5. Sobre una mesa hay 11 vasos, 5 de ellos boca arriba y 6 boca abajo. Un movimiento consiste en escoger
dos vasos cualesquiera y voltearlos simultáneamente. ¿Será posible, mediante una sucesión de estos movimientos, dejar
todos los vasos boca arriba? ¿Y dejarlos todos boca abajo?
Solución. La respuesta a la primera pregunta es afirmativa: basta tomar dos de los 6 vasos que están boca abajo y
voltearlos, voltear luego dos de los 4 vasos que quedan boca abajo y finalmente voltear los dos únicos que quedan
boca abajo. La respuesta a la segunda pregunta es negativa. En cada movimiento el número de vasos boca abajo o
permanece igual, o aumenta en 2 o disminuye en 2. Por lo tanto la paridad del número de vasos boca abajo es un
invariante, que inicialmente es par, mientras que en la posición “todos boca abajo” es impar.
Ejemplo 6. En cada uno de los 10 escalones de una escalera hay una rana. Cada rana puede dar un salto para llegar a
cualquiera de los otros escalones, pero cuando lo hace, al mismo tiempo otra rana salta la misma cantidad de escalones
pero en sentido contrario (una rana sube y la otra baja). ¿Podrán, en algún momento, quedar todas las ranas juntas
en un mismo escalón?
Solución. Numeremos los escalones del 1 al 10 y asociemos a cada rana el número del escalón que ocupa. La suma
inicial de esos valores es R = 1 + 2 + · · · + 10 = 55. Esta suma no cambia después de cada salto de dos ranas, ya que
si una rana salta m escalones la otra salta también m pero en sentido inverso, por lo que la suma no se altera. Si las
ranas, en algún momento, ocupasen un mismo escalón, digamos el n, la suma de los números asignados a cada rana
sería 10n. Pero 55 no es múltiplo de 10, luego esa situación es imposible.
2
Ejemplo 7. En cada una de las 64 casillas de un tablero de ajedrez hay un grano de azúcar. Una hormiga llega al
vértice inferior izquierdo del tablero, come el azúcar, y se traslada a una casilla adyacente, desplazándose en dirección
horizontal o vertical (pero nunca en diagonal). Continúa de este modo hasta acabar con todo el azúcar, y sin pasar
dos veces por una misma casilla. ¿Es posible que su trayecto finalice en el vértice superior derecho?
Solución. Numeremos las filas del tablero de 1 a 8, de abajo hacia arriba, y las columnas de 1 a 8, de izquierda a
derecha. Entonces cada casilla puede identificarse por sus coordenadas (fila, columna). Supongamos que la hormiga
recorre las 64 casillas del tablero y que la n-sima casilla visitada tiene coordenadas (fn , cn ). En cada movimiento fn
ó cn se incrementan o disminuyen en una unidad, por lo tanto la paridad de fn + cn cambia. Pero también cambia la
paridad de n al incrementarse en 1, por lo tanto la paridad de I = fn + cn + n permanece invariante a lo largo de todo
el recorrido. Ahora bien, al inicio del trayecto se tiene I = 1 + 1 + 1 impar. Si la última casilla visitada fuese la (8,8)
entonces se tendría I = 8 + 8 + 64, que es par, por lo tanto el trayecto no puede terminar allí.
Una forma más amena de este argumento utiliza la noción de coloración. Como se sabe las casillas del tablero
de ajedrez están pintadas de dos colores, digamos blanco y negro, en forma alternada. Cada movimiento unitario, en
dirección horizontal o vertical, nos lleva de una casilla a otra de diferente color. Ahora bien, como el tablero tiene
8 × 8 = 64 casillas, comenzando en cualquiera de ellas se requieren 63 movimientos para recorrerlas todas. Pero es
claro que después de 1, 3, 5 o cualquier número impar de movimientos estaremos en una casilla de color diferente a la
inicial. Esto demuestra que la respuesta al problema que nos ocupa es negativa, ya que un vértice y el opuesto son del
mismo color.
Ejemplo 8. En una pizarra están escritos los números 3, 4 y 12. Las operaciónes permitidas consisten en escoger
dos de los tres números, digamos a y b, y reemplazarlos por 0,6a − 0,8b y 0,8a + 0,6b. ¿Es posible, aplicando estas
operaciones, llegar a tener los números 4, 6 y 12?
Solución. Como
(0,6a − 0,8b)2 + (0,8a + 0,6b)2 = a2 + b2 ,
la suma de los cuadrados de los tres números es un invariante. Su valor inicial es 32 + 42 + 122 = 169, mientras que
42 + 62 + 122 = 196, por lo tanto no es posible llegar a tener los números 4, 6 y 12.
Nota: Si los tres números se interpretan como las coordenadas (x, y, z) de un punto en el espacio, las
p operaciones
permitidas corresponden a rotaciones alrededor de los ejes coordenados, las cuales no alteran la distancia x2 + y 2 + z 2
del punto al origen.
Ejemplo 9. (Olimpiada del Cono Sur, 2000) En el plano cartesiano, considere los puntos con ambas coordenadas
enteras y las rotaciones de 90 grados en sentido antihorario con centro en esos puntos. ¿Es posible, mediante una
sucesión de esas rotaciones, transformar el triángulo de vértices (0, 0), (1, 0) y (0, 1) en el triángulo de vértices (0, 0),
(1, 0) y (1, 1)?
Solución. Luego de algunos intentos fallidos, uno comienza a pensar que es imposible. Si se aplican las rotaciones
permitidas al punto (0,0) se pueden obtener los puntos (1,1), (-1,1), (-1,-1), (1,-1), (2,0), (0,2), etc., pero en cambio no
pueden obtenerse (1,0), (0,1), (-1,0), (0,-1), (2,1),. . . Esto nos sugiere que sólo pueden obtenerse puntos con suma de
coordenadas par, como el origen. De hecho, la paridad I(P ) = x+y mód 2 de la suma de ambas coordenadas de un punto
P = (x, y) es un invariante. En efecto, si se aplica a P la rotación R de centro (a, b) se obtiene R(P ) = (a+b−y, b−a+x).
3
La diferencia entre la suma de coordenadas de R(P ) y P es (a + b − y) + (b − a + x) − (x + y) = 2(b − y) que es par, luego
I(P ) = I(R(P )). Ahora bien, para el primer triángulo se tiene I(0, 0) = 0, I(1, 0) = I(0, 1) = 1, es decir que I es 0 en
un vértice y 1 en los dos restantes, mientras que para el segundo I(0, 0) = I(1, 1) = 0, I(1, 0) = 1. Inmediatamente se
concluye que es imposible transformar uno en otro.
Ejemplo 10. (Olimpiada Iberoamericana 2002) Dado cualquier conjunto de 9 puntos en el plano de los cuales no hay
tres colineales, demuestre que para cada punto P del conjunto, el número de triángulos que tienen como vértices a
tres de los ocho puntos restantes y a P en su interior, es par.
Solución. Si se une con un segmento cada par de puntos diferentes de P , el plano queda dividido en regiones poligonales,
una de ellas no acotada. Si P se mueve dentro de una de esas regiones entonces el número de triángulos a los que
pertenece no cambia. Pero si cruza la frontera entre dos regiones entonces sale de algunos triángulos y entra en otros.
Si una frontera es parte del segmento que une dos puntos Q y R del conjunto dado y x de los 6 puntos diferentes de
P , Q y R quedan del mismo lado de la recta QR que P , entonces al cruzar esa frontera P sale de x triángulos y entra
en otros 6 − x. El cambio neto en el número de triángulos que contienen a P es (6 − x) − x = 2(3 − x) que es par. Si
P se mueve desde su posición inicial hasta la región no acotada, el número de triángulos que lo contienen mantendrá
su paridad. Pero al llegar a la región no acotada ese número será 0, lo que completa la prueba. Observe que si en el
enunciado se cambia 9 por cualquier entero impar la conclusión es la misma.
Ejemplo 11. Considere los puntos del plano cartesiano con ambas coordenadas naturales. A partir de un punto (a, b)
está permitido moverse a (a − b, b) si a > b o a (a, b − a) si a < b. Por ejemplo la siguiente es una trayectoria válida
partiendo de (12, 7):
(12, 7) → (5, 7) → (5, 2) → (3, 2) → (1, 2) → (1, 1).
Partiendo de (86415, 69118), ¿será posible llegar hasta (1, 1)?
Solución. Si a > b entonces mcd(a − b, b) = mcd(a, b) y si a < b entonces mcd(a, b − a) = mcd(a, b), es decir que el
máximo común divisor de las coordenadas es un invariante. Como mcd(86415, 69118) = 7 y mcd(1, 1) = 1, le respuesta
es que no es posible. De hecho, las trayectorias que parten de (a, b) siempre terminan en (d, d), donde d = mcd(a, b).
Ejemplo 12. (Torneo de las Ciudades 1984) En la isla Camaleón hay 13 camaleones de color amarillo, 15 de color
verde y 17 de color rojo. Si se encuentran dos camaleones de diferente color, cambian ambos simultáneamente al tercer
color (por ejemplo si se encuentran uno amarillo y otro verde, ambos se vuelven rojos). ¿Es posible que en algún
momento todos los camaleones lleguen a ser del mismo color?
Solución. En este sistema un estado se puede describir mediante una terna (a, v, r), donde a es la cantidad de camaleones amarillos, v la de verdes y r la de rojos. Un invariante obvio es a + v + r = 45, pero no es suficiente para resolver
el problema. Analicemos lo que ocurre después del encuentro de dos camaleones. Las cantidades cambian a:
(a − 1, v − 1, r + 2), si se encuentran un camaleón amarillo y uno verde,
(a − 1, v + 2, r − 1), si se encuentran un camaleón amarillo y uno rojo,
(a + 2, v − 1, r − 1), si se encuentran un camaleón verde y uno rojo.
La diferencia de las cantidades a y v cambia, según el caso, a (a − 1) − (v − 1) = a − v, (a − 1) − (v + 2) = a − v − 3 o
(a + 2) − (v − 1) = a − v + 3. Por lo tanto, a − v es un invariante si se toma módulo 3. Si todos los camaleones en algún
momento llegaran a ser del mismo color, la diferencia a − v sería 0, 45 ó −45, es decir 0 módulo 3. Pero originalmente
a − b = 13 − 15 = −2 ≡ 1 (mód 3), por lo tanto es imposible que lleguen a ser todos del mismo color.
Otra forma de verlo: inicialmente el conjunto de restos de a, b y c módulo 3 es R = {1, 0, 2}. En cada encuentro de
dos camaleones de diferente color, dos de los números a, b y c disminuyen en 1 y el otro aumenta en 2. Pero módulo 3
aumentar en 2 es lo mismo que disminuir en 1, por lo tanto se puede decir que los tres números, tomados módulo 3,
disminuyen en 1. Por lo tanto el conjunto R es un invariante. Los camaleones no pueden llegar a ser todos del mismo
color, pues en ese caso dos de los restos serían iguales a 0.
Ejemplo 13. En el tablero de la figura está permitido cambiar de signo a todos los números de una misma fila,
columna, diagonal o paralela a una diagonal. ¿Podrá llegarse a obtener un tablero sin elementos negativos?
4
-1
1
-1
1
1
1
1
-1
1
1
-1
1
1
-1
1
1
Solución. El producto de los elementos en las casillas marcadas con x es un invariante. Como inicialmente es −1, no
es posible obtener un tablero sin elementos negativos.
x
x
x
x
x
x
x
x
Ejemplo 14. Sea n ≥ 4. Si cada uno de los números a1 , a2 ,. . . , an son 1 ó −1 y cumplen
a1 a2 a3 a4 + a2 a3 a4 a5 + · · · + an a1 a2 a3 = 0,
pruebe que n es múltiplo de 4.
Solución. Se puede introducir un proceso en este problema considerando que se parte de (a1 , a2 , . . . , an ) y que se
van cambiando los signos de los elementos negativos de uno en uno, hasta llegar a (1, 1, . . . , 1). Sea S = a1 a2 a3 a4 +
a2 a3 a4 a5 + · · · + an a1 a2 a3 . Cuando se cambia de signo un ai cambian de signo los cuatro productos en que aparece.
Pero la suma de esos cuatro productos, que son impares, es un número par 2k, y después del cambio de signo será −2k.
Luego la variación de S es −2k − 2k = −4k que es múltiplo de 4. Es decir que S mód 4 es un invariante. Inicialmente
S = 0 y al final S = n mód 4. Por lo tanto n mód 4 = 0.
Ejemplo 15. (Olimpiada Centroamericana y del Caribe 2002) En el plano coordenado se tiene la cuadrícula de n × n,
con n entero mayor o igual que 2, cuyos vértices son los puntos de coordenadas enteras (x, y), con 0 ≤ x ≤ n y
0 ≤ y ≤ n. Considere los caminos que van de (0, 0) a (n, n) sobre las líneas de esta cuadrícula y que sólo avanzan
hacia la derecha o hacia arriba. Uno de tales caminos se llama equilibrado si la suma de los valores de x de todos los
puntos por los que pasa es igual a la suma de todos los valores de y de esos mismos puntos. Muestre que todo camino
equilibrado divide al cuadrado de lado n en dos figuras de la misma área.
Solución. Sea P0 , P1 ,. . . , P2n un camino. Pongamos Pi = (xi , yi ) y llamemos L al área que queda por debajo del
camino y U al área que queda por encima. Sean Pk−1 , Pk , Pk+1 tres puntos consecutivos tales que el segmento Pk−1 Pk
sea vertical y el segmento Pk Pk+1 sea horizontal. Construyamos otro camino sustituyendo Pk por Pk′ = (xk + 1, yk − 1).
Es claro que en el nuevo camino la suma de las x’s aumenta
en 1 respecto al camino original, mientras que el área
P
debajo del camino disminuye en 1. Por lo tanto I = L + xi es un invariante para estas transformaciones elementales
de caminos. Como cualquier camino puede llevarse mediante sucesivas transformaciones
de este tipo al camino que
P
tiene n segmentos horizontales seguidos de n segmentos verticales, resulta que L + xi = 0 + (0 + 1 + 2 + · · · + n) +
(n + · · · + n)P= n(n + 1)/2 + n2 . Intercambiando losPejes se prueba
P del mismo modo que para cualquier camino se
2
cumple
U
+
y
=
n(n
+
1)/2
+
n
.
Por
tanto
L
+
x
=
U
+
yi . Esta igualdad muestra que L = U si y sólo si
i
i
P
P
xi = yi .
Ejemplo 16. (Olimpiada de Moscú 1995) Se tienen inicialmente 4 triángulos rectángulos congruentes. En un movimiento se puede tomar cualquier triángulo y partirlo en dos por la altura desde su ángulo recto. Muestre que siempre
se tiene al menos un par de triángulos congruentes.
Solución. Tomemos la hipotenusa de los triángulos iniciales como unidad y sean a y b las longitudes de los catetos.
Cada división produce triángulos semejantes al que se divide con razón a ó b.
c
b
c
1
5
b
Por lo tanto cada triángulo generado será semejante a los iniciales, con razón ai bj para ciertos enteros i, j ≥ 0. Cada
triángulo de este tipo se puede asociar con una ficha colocada en el punto de coordenadas (i, j) del plano cartesiano.
Inicialmente hay cuatro fichas en el punto (0, 0). Asignemos ahora a cada ficha ubicada en (i, j) un peso igual a 2−i−j .
La división de un triángulo de tipo (i, j) genera un triángulo de tipo (i + 1, j) y otro de tipo (i, j + 1). Esta operación
no cambia el peso total de las fichas, que es por lo tanto un invariante y su valor es el inicial, es decir 4. Ahora bien, si
en un número finito de pasos se logra que en ningún punto (i, j) haya más de una ficha, el peso total sería menor que
4, lo cual es imposible. En efecto, el conjunto de todas las fichas puede encerrarse dentro de un rectángulo de vértices
(0, 0), (n, 0), (0, m) y (n, m) y el peso de las fichas en ese rectángulo es a lo sumo
n X
m
X
i=0 j=0
3.
2−i−j =
n
X
i=0
2−i
m
X
j=0
2−j = (2 − 2n )(2 − 2m ) < 4.
Permutaciones
Sea a1 , a2 ,. . . , an una permutación de los números de 1 a n (es decir, una reordenación de los mismos). Un par
(ai , aj ) se dice que es una inversión si i < j y ai > aj . La paridad de la permutación es la paridad del número total
de inversiones que tenga. Por ejemplo la permutación 2, 3, 1, 5, 4 tiene 3 inversiones, a saber (2,1), (3,1) y (5,4), luego
es una permutación impar. La permutación (1,2,3,4,5) no tiene ninguna inversión: es par.
Si en una permutación se intercambian de lugar dos elementos contiguos ai y ai+1 , entonces el número de inversiones
disminuye en una unidad si (ai , ai+1 ) era una inversión, o aumenta en una unidad si no lo es, por lo tanto la paridad
de la permutación cambia. Más en general, si se intercambian de lugar dos elementos cualesquiera ai y aj (operación
que se llama transposición) la paridad de la permutación cambia. En efecto, si i < j el intercambio puede realizarse
transponiendo sucesivamente ai con ai+1 , ai+2 ,. . . aj y luego aj con aj−1 , aj−2 ,. . . ai+1 . Como en total se realizaron
2(j − i) − 1 transposiciones de elementos contiguos, la paridad cambió un número impar de veces, es decir que cambió.
Ejemplo 17. En la pizarra están escritos los números del 1 al 10 en orden creciente:
1 2 3 4 5 6 7 8 9 10
Una operación permitida consiste en seleccionar cuatro números, intercambiar el primero con el cuarto y el segundo
con el tercero. Analice la posibilidad de que alguna secuencia de estas operaciones produzca como resultado
10 9 8 7 6 5 4 3 2 1.
Solución. Las operaciones permitidas equivalen a efectuar dos transposiciones, por lo tanto cambian la paridad dos
veces, es decir que la dejan igual. Tenemos así un invariante.
La permutación inicial (1,2,3,4,5,6,7,8,9,10) no tiene inversiones, mientras que (10, 9, 8, 7, 6, 5, 4, 3, 2, 1) tiene
9 + 8 + 7 + · · · + 1 = 45 inversiones. Como 0 y 45 son de diferente paridad, el segundo estado es inaccesible desde el
primero.
Ejemplo 18. En 1878 Sam Loyd propuso un rompecabezas que ha mantenido su popularidad hasta nuestros días.
En una caja hay 15 fichas cuadradas, numeradas del 1 al 15, dispuestas como se ve en el siguiente diagrama.
1
2
3
4
5
6
7
8
9
10
11
12
13
15
14
6
La casilla inferior derecha está vacía, y si los números se leen de izquierda a derecha y de arriba hacia abajo entonces
están ordenados en forma creciente, excepto por el 15 y el 14 que aparecen transpuestos. Un movimiento válido
consiste en deslizar una de las fichas adyacentes a la casilla vacía hasta ocuparla. ¿Es posible, mediante una secuencia
de movimientos válidos, intercambiar el 14 y el 15 dejando a los demás números en su posición inicial? Sam Loyd
ofreció 1000 dólares de premio a quien lo lograse, generando una verdadera fiebre entre la gente que procuraba hallar
la solución. Sin embargo nadie logró cobrar el premio...
Solución. No es posible. Numeremos las filas de 1 a 4, de arriba hacia abajo. A cada posición del juego del 15 le
podemos asociar una permutación de los números del 1 al 15, leyendo cada fila de izquierda a derecha, desde la 1
hasta la 4, sin tomar en cuenta la casilla vacía. A la posición inicial le corresponde la permutación 1, 2, 3, 4, 5, 6, 7,
8, 9, 10, 11, 12, 13, 15, 14, que tiene una sola inversión, a saber la (15, 14), y por lo tanto es impar. La permutación
que había que obtener para ganar el premio era simplemente la sucesión ordenada de los números del 1 al 15, que es
par. Es claro que los movimientos horizontales no modifican en nada la permutación ni la fila en que se encuentra la
casilla vacía. En cambio si se mueve un número hacia abajo el efecto será que este número adelanta a los tres que le
siguen, lo que equivale a efectuar tres transposiciones sucesivas, y la paridad de la permutación cambia. Pero en este
caso cambia también la paridad de la fila ocupada por la casilla vacía. En consecuencia la suma módulo 2 del número
de fila en que se encuentra la casilla vacía y la paridad (par = 0, impar = 1) de la permutación de los números en las
fichas, es un invariante. En la posición inicial este invariante es 1, y en la que se quiere lograr es 0.
4.
Juegos de estrategia
Los juegos a los cuales nos referimos en esta sección pueden conceptualizarse como sistemas que pueden estar
en cierto número de estados, también llamados posiciones del juego. Debe haber un estado inicial y uno o más
estados finales. El estado del juego puede cambiar como consecuencia de las jugadas que realizan los contendientes,
siguiendo reglas específicas. Un juego puede ser unipersonal (como los conocidos solitarios que se juegan con cartas)
o pluripersonal. Cuando se llega a una posición final la partida termina y las reglas del juego determinan qué jugador
es el ganador, o si hay empate. Una estrategia ganadora es un método de juego que asegura la victoria al jugador que
la aplica.
A continuación consideraremos juegos bipersonales, en los cuales participan dos jugadores que convencionalmente
llamaremos A y B. Una partida se inicia en el estado inicial, y su desarrollo consiste en que A y B realizan jugadas
de manera alternada, comenzando por A. Supondremos que el juego es de información perfecta, es decir que ambos
jugadores tienen pleno conocimiento del juego, de sus reglas y de las jugadas que cada uno ha realizado. En particular,
no hay jugadas ocultas ni interviene para nada el azar. También supondremos que el juego es finito, es decir que cada
jugador, en su turno, tiene a su disposición un número finito de jugadas posibles para elegir y que toda partida finaliza
(llega a una posición final) en un número finito de jugadas. Si no hay posibilidad de empate (es decir, si toda partida
finaliza con un ganador y un perdedor) vale el siguiente resultado:
Teorema de Zermelo
En un juego bipersonal finito de información perfecta y sin posibilidad de empate, uno de los dos jugadores tiene
una estrategia ganadora.
Las estrategias ganadoras suelen estar ligadas a invariantes, como en los siguientes problemas.
Ejemplo 19 (OMCC 2002).
Dos jugadores A, B y otras 2001 personas forman un círculo, de modo que A y B no quedan en posiciones consecutivas.
A y B juegan por turnos alternadamente empezando por A. Una jugada consiste en tocar a una de las personas que se
encuentra a su lado, la cual debe salir del círculo. Gana el jugador que logre sacar del círculo a su oponente. Demostrar
que uno de los dos jugadores tiene una estrategia ganadora y describir dicha estrategia.
Solución. Como 2001 es impar, en uno de los arcos que separan A de B hay un número par de personas interpuestas
y en el otro una cantidad impar. Si A logra que se repita esa situación cada vez que sea su turno entonces ganará
el juego, ya que la reducción del número de personas hará que eventualmente B quede a su lado. Esto lo logra A
7
fácilmente tocando a su vecino en el arco par, dejando así un número impar de personas en cada arco. Al jugar B
vuelven a quedar un arco par y otro impar.
Ejemplo 20 (Juego de Bachet). En un montón hay 100 piedras. Dos jugadores A y B juegan alternadamente,
comenzando por A. Cada jugador puede retirar como mínimo una y como máximo cinco piedras. Gana el que retire
la última piedra. ¿Tiene alguno de ellos una estrategia ganadora? ¿Cuál es esa estrategia?
Solución. Por el Teorema de Zermelo alguno de los dos jugadores tiene una estrategia ganadora, el problema es
determinar cuál de los dos la tiene, y cuál es esa estrategia. Parte de la dificultad de este problema es el gran número
de piedras inicial, que hace muy difícil un análisis exhaustivo de todas las jugadas posibles. Lo indicado en estos
casos es simplificar el problema, para lo cual podemos estudiar qué sucede para valores pequeños del número inicial
de piedras n. Para n = 1 obviamente A la retira y gana. Lo mismo ocurre si n = 2, 3, 4 ó 5. En cambio si n = 6
quien tiene una estrategia ganadora es B, ya que juegue lo que juegue A en el montón quedarán de 1 a 5 piedras, y
B gana retirándolas todas. Si n = 7, A puede ganar retirando 1 y dejándole 6 a B. Del mismo modo si n = 8, 9, 10
u 11, A gana retirando respectivamente 2, 3, 4 ó 5 piedras. Pero para n = 12 quien tiene una estrategia ganadora es
nuevamente B. En general, si n es múltiplo de 6, B tiene una estrategia ganadora. Lo que debe hacer, si A retira k
piedras (1 ≤ k ≤ 5), es retirar 6 − k piedras, dejando nuevamente un múltiplo de 6 en el montón. Así el montón llegará
eventualmente a 0, ganando B. En cambio si n no es múltiplo de 6, quien tiene una estrategia ganadora es A. En su
primera jugada debe retirar un número de piedras igual al resto de la división de n entre 6, para así dejarle a B un
múltiplo de 6. En lo sucesivo juega dejando siempre un múltiplo de 6 en el montón.
En este ejemplo n = 100, que no es múltiplo de 6, por lo tanto A tiene una estrategia ganadora. En su primera
jugada debe retirar 4 piedras y en lo sucesivo jugar de modo de dejarle siempre a su oponente un múltiplo de 6.
5.
Subinvariantes
Un subinvariantes es una función S : E → R tal que, si Ei → Ej es una transición válida, entonces S(Ei ) ≤ S(Ej ).
Si el estado B es accesible desde A entonces evidentemente S(B) ≤ S(A). Por lo tanto si S(B) > S(A) podemos
concluir que B es inaccesible desde A. Por esta razón los subinvariantes suelen ser tan útiles como los verdaderos
invariantes. Un caso particular importante se presenta cuando el subinvariante toma valores enteros no negativos. En
este caso no puede haber una sucesión infinita estrictamente decreciente de valores de S, por lo tanto a partir de cierto
instante los valores de S deben estabilizarse y ya no cambiarán.
Ejemplo 21. En un parlamento unicameral cada miembro tiene a lo sumo 3 enemigos. Muestre que el parlamento se
puede dividir en 2 cámaras, de manera que cada miembro tenga a lo más un enemigo en la cámara en que quede.
Solución. Distribuya las personas en dos cámaras A y B de cualquier manera. Si una persona tiene más de un enemigo
en el comité en que está, cámbiela a la otra cámara, donde tendrá a lo sumo un enemigo. La suma del número de pares
de enemigos en cada cámara es entonces un subinvariante que toma valores enteros no negativos. Cuando llegue a su
valor mínimo se habrá logrado el objetivo.
Ejemplo 22. En un tablero cuadrado de 100 × 100 hay 99 casillas infectadas. Si una casilla tiene dos o más lados
comunes con casillas infectadas, ella también se infecta por contagio. ¿Es posible que en algún momento todas las
casillas del tablero estén infectadas?
Solución. No es posible. El perímetro P de la figura formada por las casillas infectadas es un subinvariante, ya que
cuando una casilla sana se infecta al menos dos lados comunes con casillas previamente infectadas dejan de pertenecer
al borde de la figura, mientras que a lo sumo otros dos se incorporan al borde. Si todas las casillas se infectasen P
terminaría siendo 400, pero el valor inicial de P es a lo sumo 99 × 4 < 400.
Ejemplo 23. (Subiendo al cielo) Consideremos en el plano cartesiano la cuadrícula cuyos vértices son los puntos con
ambas coordenadas enteras. Supongamos que se colocan fichas en celdas ubicadas debajo de la línea y = 0 (a lo sumo
una ficha por celda). Una ficha puede saltar sobre otra contigua hasta una casilla vacía, y la ficha sobre la cual se salta
se retira (como en el juego de damas). Llamemos coordenadas de una celda unitaria a las coordenadas de su vértice
inferior izquierdo. ¿Para qué valores de n ≥ 0 es posible llevar una ficha hasta la celda (0, n)?
8
Solución. Con dos fichas en (0 − 1) y (0, −2) se puede llegar a colocar una ficha en (0,0):
b
b
b
b
O
O
b
Con cuatro fichas se puede llegar a colocar una ficha en (0,1):
b
b
b
b
b
b
b
b
b
b
Del mismo modo con 8 fichas dispuestas como muestra la figura
b
b
b
b
b
b
b
b
es fácil ver que se puede alcanzar (0, 2). Y con 21 fichas se puede alcanzar (0, 3) (esto se deja como ejercicio). Podría
pensarse entonces que, comenzando con un número suficiente de fichas, se podría alcanzar cualquier altura. Pero en
realidad no es así, de hecho ¡la celda (0, 4) es inalcanzable! Para probarlo construiremos un subinvariante. La idea es
tratar de expresar la «energía» de una configuración sumando las energías E(x, y) de cada una de las fichas. La energía
de una ficha ubicada en la celda (0, y + 2) debe ser igual a la suma de dos fichas ubicadas en (0, y) y (0, y + 1), es decir
E(0, y + 2) = E(0, y) + E(0, y + 1).
Esto puede verse como una relación de recurrencia, de hecho la famosa recurrencia
de Fibonacci, que tiene la solución
√
E(0, y) = ry , si r2 = r + 1. La raíz positiva de esta ecuación es ϕ = (1 + 5)/2 (la razón áurea).
Si deseamos colocar una ficha en una celda (0, y) con el mayor y posible, los únicos movimientos razonables parecen
ser los ascendentes y los horizontales dirigidos hacia el eje de las y. La misma ley de conservación puede obtenerse
para estos movimientos tomando E(x, y) = ϕy−|x| . Finalmente, si S es un conjunto de celdas con fichas, definimos
E(S) =
√ !y−|x|
1+ 5
.
2
X
(x,y)∈S
Observamos que el valor de E(S) se mantiene si se efectúan movimientos «en la dirección correcta», es decir hacia
arriba u horizontales hacia el centro. Para otros movimientos, E(S) disminuye (es decir que es un subinvariante).
Ahora bien, la energía de una ficha en la celda (0, 4) es ϕ4 . Si se coloca una ficha en cada celda (x, y) con y < 0,
la energía total sería
!
−1
+∞
−1
∞
−1
X
X
X
X
X
2ϕ−1
y−|x|
y
−x
y
ϕ
=
ϕ 1+
ϕ
=
ϕ 1+2
1 − ϕ−1
y=−∞ x=−∞
y=−∞
y=−∞
x=1
−1
1 + ϕ−1 X y
1 + ϕ−1 ϕ−1
ϕ+1
=
ϕ =
=
,
−1
1 − ϕ y=−∞
1 − ϕ−1 1 − ϕ−1
(ϕ − 1)2
9
pero como ϕ(ϕ − 1) = ϕ2 − ϕ = 1 resulta
ϕ2
ϕ4
=
= ϕ4 .
2
(ϕ − 1)
(ϕ(ϕ − 1))2
Esto significa que ninguna cantidad finita de fichas en el semiplano y < 0 logra alcanzar la energía ϕ4 (y una cantidad
infinita nunca permitiría llegar en un número finito de pasos hasta (0, 4)).
6.
Referencias
El siguiente libro dedica su primer capítulo al Principio de Invariancia y contiene problemas de todos los grados
de dificultad:
Engel, A., Problem-Solving Strategies, Springer, New York, 1998.
Vea también la sección 3.4 de
Zeitz, P., The Art and Craft of Problem Solving, 2nd ed., John Wiley & Sons, 2007.
El Capítulo 12 del siguiente libro contiene problemas interesantes y accesibles sobre invariantes:
Fomin, D., Genkin, S., Itenberg, I. V. , Mathematical Circles (Russian Experience), American Mathematical
Society, 1996.
Un análisis elemental del juego del 15 puede verse en
Nieto, J. H., Permutaciones y el Juego del 15, Boletín de la Asociación Matemática Venezolana, 12(2) (2005),
259–264. Este artículo está disponible en
http://www.emis.de/journals/BAMV/conten/vol12/jnieto.pdf
En http://www.jhnieto.org/15-1.htm se puede practicar el juego del 15 en línea.
En http://www.jhnieto.org/sube.htm se puede jugar “Subiendo al cielo” en línea.
10