Variables aleatorias. Distribución Gaussiana. Simulación Montecarlo.

Series Temporales: sesión 2 (13/10/2009)
Ejercicio propuesto: Halla la esperanza y la varianza del siguiente proceso en tiradas independientes.
Xt =
t
X
θτ
(1)
τ =1
θτ =
1
con probabilidad p
−1 con probabilidad 1 − p
(2)
Solución:
E(Xt ) = E(
t
X
θτ ) =
τ =1
t
X
t
X
E(θτ ) =
(p + (−1)(1 − p)) = t(2p − 1)
τ =1
(3)
τ =1
Para poder hallar la varianza, primero hallamos el momento de orden 2
t X
t
t X
t
t
X
X
X
θτ )2 ) = E(
θτ θτ 0 ) =
E(θτ θτ 0 )
E(Xt2 ) = E((
τ =1 τ 0 =1
t
X
τ =1
=
X
E(θτ2 )
E(θτ )E(θτ 0 ) +
τ 6=τ 0
τ =1 τ 0 =1
τ =1
2
= t(t − 1)(2p − 1) + t(12 p + (−1)2 (1 − p))
= (2p − 1)2 t2 + t(1 − (2p − 1)2 ) = E(Xt )2 + t(4p − 4p2 )
⇒ V ar(Xt ) = 4p(1 − p)t
(4)
Podemos señalar que el proceso Xt es un proceso de difusión, puesto que
su varianza es lineal respecto al tiempo
Números aleatorios
Distribuciones discretas: en la sesión anterior ya vimos la distribuciı̈¿ 21 n
binomial
N
PN (m) =
(1 − p)N −m pm
(5)
m
Otra distribución discreta muy importante es la distribución de Poisson. Una
variable se dice de Poisson de media λ si
k
−λ λ
P (X = k) = e
k!
(6)
Distribuciones continuas:
Las distribuciones continuas se caracterizan por dos tipos de funciones:
la función de densidad de probabilidad pdf (x|θ) y la función de probabilidad
acumulada cdf (x|θ), donde θ es el vector de parámetros de los que depende
la distribución. Ambas se relacionan por la siguiente igualdad:
Z x
pdf (x0 |θ)dx0
(7)
P (X ≤ x) ≡ cdf (x|θ) =
∞
Distribución Gaussiana o Normal
1
(x − µ)2
p(x) = normpdf (x|µ, σ) = √
exp −
2σ 2
2πσ
(8)
Distribución Log-normal
1 1
(log y − µ)2
p(y) = lognpdf (y|µ, σ) = √
exp −
2σ 2
2πσ y
(9)
Veamos algunas propiedades de la distribución normal. Si tenemos X ∼
N (µ, σ), una variable aleatoria normal de parámetros µ y σ, podemos hacer
una cambio de variable para trabajar con una va Z ∼ N (0, 1):
dx
x−µ
⇒ dz =
⇒ px (x)dx = pz (z)dz ⇒ px (x)σ = pz (z)
σ
σ
2
1
z
pz (z) = √ exp −
⇒ Z ∼ N (0, 1)
2
2π
(10)
R∞
Demostración de que −∞ p(z)dz = 1:
Z ∞
z2
I=
exp (− )dz
(11)
2
−∞
z =
I
2
2 Z ∞
Z ∞
z2
x2
y2
exp (− )dz =
exp (− )dx
exp (− )dy
2
2
2
∞
∞
−∞
Z ∞Z ∞
2
2
x +y
exp −
dxdy
2
−∞ −∞
Z 2π Z ∞
∞
r2
r2
dθ
r exp (− )dr = 2π[− exp (− )]
2
2 0
0
0
Z ∞
2
√
1
z
I = 2π ⇒ √
exp (− ) = 1
2
2π −∞
(12)
Z
=
=
=
⇒
∞
donde hemos utilizado un simple cambio a coordenadas polares.
Cálculo de momentos:
Los momentos de potencia impar son siempre igual a cero, dado que la función
a integrar es impar respecto al origen, y el intervalo de integración es simétrico
respecto al origen:
E(z 2k+1 ) =
Z
∞
1
z 2k+1 p(z)dz = √
2π
−∞
Z
∞
z2
z 2k+1 e 2 = 0
−
(13)
−∞
Los momentos pares cumplen la siguiente igualdad (queda como ejercicio
para la siguiente sesión):
E(z 2k ) = (2k − 1)!!
(14)
Un primer paso para la demostración por inducción es demostrar que E(z 2 ) =
(2 − 1)!! = 1 (para terminar el ejercicio tendremos que aplicar inducción):
"
2 #∞
Z ∞
Z ∞
− z2
2
z
1
z2
1
−ze
√
√
√
z(z exp (− ))dz =
+
exp (− )dz = 1
2
2
2π −∞
2π
2π −∞
−∞
(15)
Para resolverla hemos utilizado la fórmula de integración por partes,
Z
Z
udv = uv − vdu
(16)
z2
donde u = z y dv = z exp (− ), y que la integral de la densidad de proba2
bilidad es 1.
Ejercicio: Siendo X una va. normal de media µ y desviación estándar σ,
demuestra que E((x − µ)2k+1 ) = 0 y que E((x − µ)2k ) = (2k − 1)!!σ 2k .
Otros datos de la normal están recogidos en la siguiente tabla:
Media
Varianza
Coef. de asimetrı́a
Kurtosis
E(x)
E((x − µ)2 )
E((x − µ)3 )
σ3
E((x − µ)4 )
σ4
µ
σ2
0
3
La kurtosis es una medida de lo ”picuda”que es la pdf. Si kurtosis > 3
entonces la pdf es leptokúrtica o de cola pesada, como la pdf log-normal o la
distribución de Cauchy/Lorenz. Si kurtosis < 3 entonces la pdf se considera
platokúrtica o de cola ligera.
Método de Montecarlo
Supongamos que tenemos un generador de muestras aleatorias de una
cierta distribución. Podemos representar en un histograma de cajas la cantidad de muestras generadas en cada intervalo definido. Cuando la cantidad
de muestras generadas tiende a infinito, entonces el histograma se aproxima
a la pdf de la distribución.
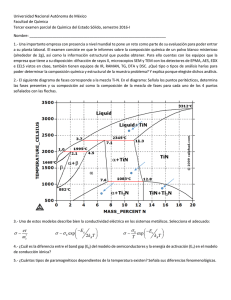
Figura 1: Histograma de una distribución normal.
¿ Cómo podemos estimar E(x) mediante muestreo?
Sean {xi }N
i=1 variables aleatorios independientes e idénticamente distribuidas
(iid) xi ∼ N (µ, σ), entonces
N
1 X
E[x] ≈
xi
N i=1
(17)
Teorema del lı́mite central para estimaciones Montecarlo
Sean {ξi }N
i=1 , N variables aleatorias independientes e idénticamente distribuidas,
de media E[ξ] y desviación estándar std[ξ],
N
1 X
ξi = E[ξ] + ,
N i=1
(18)
donde para N → ∞
std[ξ]
∼ N (0, √ ).
N
Escrito en Latex por Vı́ctor Soto Martı́nez.
(19)