Document

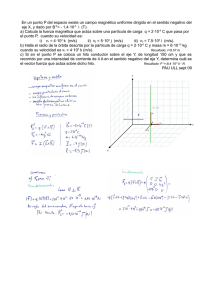
Tema 2. Sistemas conservativos
Segunda parte: Potenciales centrales
• Un potencial U se denomina central cuando depende solamente de la distancia
a un punto fijo O. Tomando un sistema de referencia centrado en O, el potencial sólo
depende de la coordenada radial U = U (r ). La fuerza generada por la presencia de este
potencial es
r
r
r
dU r
F = −∇U (r ) = −
ur = F (r ) ur
dr
Consecuentemente, una fuerza central es aquella que está dirigida hacia, o desde, un
punto fijo O, y cuyo módulo sólo depende de la distancia a O. A continuación
enumeramos las principales características del movimiento bajo un potencial central.
A) Se conserva el momento angular respecto a O
• El momento de la fuerza respecto a O es
r r r
r r
M = r × F = F (r ) r × u r = 0
y de la ley de Newton para el movimiento de rotación respecto a O
r
r dL
M=
=0
dt
se concluye que el momento angular respecto al centro de fuerza O es constante
r
r
r r
r
L = r × mv = cte
Como
consecuencia, r y v deben estar contenidos en el plano perpendicular al vector
r
L , y la posición de dicho plano no varía en el tiempo. La órbita está contenida en ese
plano. Dada la simetría del problema respecto a la rotación según el eje definido por el
r
vector L , es conveniente tomar un sistema de coordenadas polares (r , φ ) en el plano de
la órbita, centrado en el punto O.
B) El movimiento cumple la ley de las áreas
• Respecto al sistema de coordenadas polares, la posición y velocidad tienen la
expresión
r
r
r = r ur
r
r
r
v = r& ur + rφ& uφ
El momento angular respecto a O es
v
r
r
r
r
L = r u r × m r& u r + rφ& uφ = mr 2φ& u z
(
)
y la condición de conservación de su módulo nos lleva a la constante del movimiento
L = mr 2φ&
• Definimos la velocidad areolar como la derivada respecto al tiempo, del área S
barrida por el radio vector al moverse la partícula en el plano de la órbita.
v areolar =
dS
dt
La ley de las áreas establece que la velocidad areolar es constante, es decir, se recorren
áreas iguales en tiempos iguales. Equivale a la conservación del módulo L del momento
angular. Como demostración, supongamos que una partícula se encuentra en el instante
t en la posición A, y en el instante t+dt en la posición B.
B(t+dt)
r+
dr
y
dS
dφ
r
O
A(t)
x
La partícula recorre en el intervalo dt la distancia ds ≈ r dφ . El área barrida es igual al
área del triángulo AOB
1
1
dS = r (rdφ ) = r 2dφ
2
2
con lo cual la velocidad areolar es
dS 1 2 dφ 1 2 &
= r
= rφ
dt 2 dt 2
Introduciendo la conservación del momento angular, obtenemos la fórmula matemática
de la ley de la áreas
dS
1
L
=
mr 2φ& =
dt 2 m
2m
C) Ecuaciones del movimiento
• Escribimos la ley de Newton en coordenadas polares
r
r
F = ma
donde la aceleración del cuerpo tiene la expresión
r
r
r
a = &r& − rφ& 2 ur + rφ&& + 2 r&φ& uφ
(
)
con lo cual, la ley del movimiento es
(
)
(
F (r ) = m &r& − rφ& 2
)
y
(
)
d
mr 2φ& = 0
dt
La última ecuación expresa la conservación del momento angular.
D) Conservación de la energía
• Se define la energía de la partícula como la suma de la energía cinética y la
energía potencial
1 r
E = mv2 + U (r )
2
Derivando respecto al tiempo, vemos que la energía se conserva, es una constante del
movimiento
r r r r
r
r r
dE
= mv ⋅ a + v ⋅ ∇U (r ) = v ⋅ ma + ∇U (r ) = 0
dt
(
E)
)
Potencial centrífugo. Potencial efectivo
• Utilizamos la conservación de la energía para integrar el sistema, y encontrar la
solución que defina su movimiento. En coordenadas polares
v 2 = r&2 + r 2φ&2
Con ayuda del teorema de conservación del momento angular, podemos eliminar la
variable angular φ , resultando
v 2 = r& 2 + r 2
L2
L2
2
&
=
r
+
m 2r 4
m2r 2
Así, la energía del sistema queda definida como función exclusivamente de la distancia
radial r,
1  2
L2 
1 2
L2
E = m r& + 2 2  + U (r ) = m r& +
+ U (r )
2 
2
mr 
2 mr 2
Se comprueba entonces que el problema es similar al estudiado en la primera parte de
este tema (dinámica de la partícula en una recta), ya que la partícula se ve sometida al
potencial efectivo en la dirección radial
L2
+ U (r )
2mr 2
función exclusiva de la variable radial r. El primer término se llama potencial
centrífugo y da lugar a una fuerza repulsiva radial, debida a la rotación respecto a O
L2
Uc =
2mr 2
U ef =
F) Tipos de movimiento
• La región accesible para la partícula es aquella en la que E ≥ U ef (r ). Si E es
igual a un mínimo del potencial efectivo U ef tenemos estados de equilibrio en los
cuales r es constante (r& = 0 ). Es decir, son trayectorias circulares centradas en O. Para
energías ligeramente superiores a estos mínimos de potencial se producen oscilaciones
en torno a las órbitas circulares, que para algunos potenciales toman la forma de
trayectorias elípticas con uno de los focos en O.
• Los puntos de retroceso del movimiento radial son las soluciones de
E = U ef (r ) . La trayectoria se mantiene acotada entre dos circunferencias si existen dos
puntos de retroceso radial. Si no, la partícula llega al infinito, o bien, cae al centro de
fuerzas O.
G) Cálculo de órbitas. Fórmulas de Binet
• Partimos de las ecuaciones del movimiento
(
F (r ) = m &r& − rφ& 2
)
y
L = mr 2φ&
Suponemos que la dependencia temporal de r es de la forma
r (t ) = r[φ (t )]
con lo cual, las derivadas temporales adquieren la forma
dr dφ dr & dr
=
=φ
dt dt dφ
dφ
y
d 2 r d 2φ dr  dφ  d 2 r && dr & 2 d 2 r
= 2
+ 
=φ
+φ
dφ
dt 2
dt dφ  dt  dφ 2
dφ 2
2
• Derivando respecto al tiempo la ecuación que define el módulo del momento
angular L, encontramos
r 2φ&& + 2rr&φ& = 0
con lo cual, la derivada segunda adquiere la expresión
2
d 2 r & 2  d 2 r
1  dr  
=φ
−2  
 dφ 2
r  dφ  
dt 2


• Introduciendo estas derivadas temporales en la ley del movimiento en la
dirección radial, vemos que se satisface
2
F (r ) & 2  d 2 r
1  dr  
=φ
− 2   − rφ& 2
2

m
r  dφ  
 dφ

2
Eliminando φ& con ayuda de la conservación del momento angular, llegamos a la
conclusión de que la órbita de la partícula r = r (φ ) es solución de la ecuación
diferencial
mr 4 F (r ) d 2r
1  dr 
= 2 −2   −r
2
r  dφ 
L
dφ
2
• Esta ecuación se simplifica con el cambio de variable
u=
1
r
con el resultado
d 2u
m 1
2 + u = − 2 2 F 
dφ
u L u 
que se conoce como la 2ª fórmula de Binet, para la órbita bajo una fuerza central F (r ) .
Nos sirve para calcular la trayectoria de la partícula si conocemos la fuerza central, o
para calcular la ley de fuerza si conocemos la trayectoria de la partícula.
• La 1ª fórmula de Binet relaciona el campo de velocidades con la órbita de la
partícula. Es decir, nos permite conocer el módulo de la velocidad en los distintos
puntos de la órbita recorrida por la partícula. Con los mismos pasos anteriores,
2
2

L2
L2
L2   dr 
2  dr 
&
v = r& + 2 2 = φ   + 2 2 = 2 4    + r 2 
mr
m r   dφ 
 dφ  m r

2
2
ó en función de la variable u
2

L2   du 
v = 2    + u 2 
m   dφ 

2
Problemas Resueltos
2.5
Una partícula de masa m describe una trayectoria circular de radio R que
pasa por el centro de fuerzas O. Determinar en función de m, R, y de la velocidad
mínima de la partícula en su trayectoria,
a) la ley de velocidades,
b) la ley de la fuerza
c) la energía potencial de la partícula.
y
m
r
O
φ
R
x
y
• La trayectoria en coordenadas polares es
m
r = 2R cos φ
como se puede deducir de la siguiente gráfica
r
90º
φ
O
2R
Respecto a la variable u obtenemos
u=
1
2 R cosφ
y de aquí,
du
sin φ
=
= u tan φ
dφ 2R cos2 φ
u2
 du 
2
2
2
= 4R 2u 4
 dφ  + u = u (1 + tan φ ) =
2
cos φ
 
2
x
• Utilizando la 1ª fórmula de Binet, hallamos la ley de velocidad de la partícula en
función de la posición en la órbita
2

L2   du 
L2 2 4 4 R 2 L2
2
v = 2   + u  = 4 2 R u = 2 4
m   dφ 
m
mr

2
ó
v=
2 RL
mr 2
Debemos expresar el resultado en función de la velocidad mínima de la masa m en la
trayectoria. La velocidad alcanza su valor mínimo cuando la coordenada radial r sea
máxima, es decir, en r = 2 R . Dicho valor mínimo es
L
2mR
v min =
con lo cual, la velocidad de la partícula satisface
 2R 
v = vmin 

 r 
2
• Para determinar la fuerza central F(r) que genera este tipo de órbita utilizamos la
2ª fórmula de Binet. Ahora
d 2u d
2u
u
2
=
φ
=
φ
+
=
−
+
= −u + 8R 2u 3
u
tan
u
tan
u
(
)
2
2
2
dφ
dφ
cos φ
cos φ
con lo cual
Lu
1 
F  = −
m
u 
2
2
 d 2u

8 R 2 L2u 5
8 R 2 L2
 2 + u  = −
=−
= F (r )
m
mr 5
 dφ

En función de la velocidad mínima, la fuerza central tiene la expresión
mv2min  2 R 
F (r ) = −
 
R  r 
5
fuerza atractiva, inversamente proporcional a la quinta potencia de r.
• La energía potencial satisface
F (r ) = −
dU
dr
Integrando esta ecuación, con la condición de que la energía potencial se anule en el
infinito, obtenemos
∫
r
mv2min
U (r ) = − F (r ) dr =
R
∞
∫
r
∞
5
mv 2min  2R 
 2R 
dr
=
−
 r 
2  r 


4
2.6
Una partícula de masa m describe una espiral bajo la acción de una fuerza
central. Deducir la ley de fuerza, si la espiral está descrita por la ecuación r =
a
.
φ
r
φ
O
• Utilizamos la 2ª fórmula de Binet. En función de la variable u, la órbita se
describe por la ecuación
1
u= φ
a
La fuerza central que genera este tipo de movimiento satisface
L2u 2
L2u 3
L2
1
′
F  = −
(u + u ) = − m = − 3 = F (r )
m
mr
u 
Por tanto, es una fuerza atractiva inversamente proporcional al cubo de la distancia al
centro de fuerzas.
2.7
Una partícula de masa m se mueve en una región donde existe un potencial
central de la forma U (r ) = kr , k > 0 . ¿Para qué valores de la energía y del
momento angular la órbita será una circunferencia de radio a con centro en O?
¿ Cuál es el período de revolución en esa órbita? Si el movimiento de la partícula
se perturba separándolo de dicho movimiento circular, ¿cuál será el período de las
oscilaciones radiales alrededor de r = a .
4
• Por ser el potencial central se conserva la energía y el momento angular respecto
a O. En una órbita circular de radio a, el equilibrio de las fuerzas en la dirección radial
se escribe
Fc = F (a )
siendo Fc la fuerza centrífuga, y F (a ) la fuerza central evaluada en r = a . Por
definición, la fuerza central deriva del potencial en la forma
F (r ) = −
dU
= −4kr 3
dr
y es una fuerza atractiva, dirigida hacia el centro O.
La fuerza centrífuga, generada por la rotación respecto al centro O es
Fc = m
v2
a
con lo cual, del equilibrio de fuerzas, obtenemos la velocidad en la órbita circular
v2
= 4ka 3
a
k 2
v=2
a
m
m
• La energía del sistema es suma de la energía cinética y la energía potencial
E =m
v2
4 ka 4
+ U (a ) = m
+ ka 4 = 3ka 4
2
2m
y el momento angular para la trayectoria circular es
L = mav = 2 mk a 3
El hecho de que la energía de la partícula sea menor que la energía potencial en el
infinito, en este caso equivale a que sea finita, indica que la partícula no puede escapar
al infinito. La partícula está atrapada en el campo de fuerza.
• La trayectoria circular se describe con velocidad constante v, siendo el período
de revolución igual a
T=
2πa π m
=
v
a k
• Cuando la partícula se ve desplazada ligeramente de esta órbita circular, su
energía potencial U(r) admite el desarrollo en serie
1
2
U (r ) ≈ U (a ) + U ′(a )(r − a ) + U ′′(a )(r − a )
2
y de aquí, la fuerza central que sufre la partícula, en las inmediaciones de la órbita
circular, es
F (r ) ≈ −U ′(a ) − U ′′(a )(r − a )
Suponemos que la perturbación no afecta al momento angular de la partícula, que se
mantiene constante. La fuerza centrífuga para posiciones cercanas al movimiento
circular también admite el desarrollo
Fc (r ) ≈ Fc (a ) + Fc′(a )(r − a )
• La ley de movimiento para el movimiento radial es
d 2r
m 2 = F (r ) + Fc (r )
dt
y sustituyendo los desarrollos anteriores, obtenemos la ecuación del movimiento en la
vecindad de la órbita circular
d 2r
m 2 = −U ′(a ) − U ′′(a )(r − a ) + Fc (a ) + Fc′(a )(r − a )
dt
• Definimos la variable para el movimiento perturbado como la distancia radial a la
órbita circular
s = r −a
La ley de movimiento para la variable s es
d 2s
m 2 + [U ′′(a ) − Fc (a )]s = −U ′(a ) + Fc (a )
dt
El lado derecho es nulo en virtud de la condición equilibrio en la órbita circular, por lo
que obtenemos finalmente
d 2s
m 2 + [U ′′(a ) − Fc (a )]s = 0
dt
que corresponde a una oscilación armónica cuya frecuencia de movimiento satisface
ω2 =
U ′′(a ) − Fc′(a )
m
• Evaluando las derivadas espaciales
U ′′(a ) = 12ka 2
teniendo en cuenta el valor constante del momento angular L
Fc′(a ) = −3
L2
4mka 6
=
−
3
= −12ka 2
4
4
ma
ma
obtenemos la frecuencia de oscilación del movimiento perturbado alrededor de la órbita
circular
ωp = 2 6
k
a
m
y el período de las oscilaciones radiales
Tp =
π
m
a 6 k
lo que indica que el movimiento de oscilación radial es más lento que el movimiento
orbital en un factor
6.
2α
, dirigida perpendicularmente
3a 3
al radio vector, a una distancia a del centro O de una fuerza central atractiva
mα
− 4 . Calcular el tiempo de caída al centro de fuerzas.
r
2.8
Una partícula se lanza con velocidad
• Utilizamos el concepto de potencial efectivo. La ley del movimiento para la
coordenada radial r se obtiene de la conservación de la energía
1 2
L2
&
E = mr +
+ U (r )
2
2mr 2
donde U(r) es la energía potencial de la partícula. Por definición,
U (r ) = −
∫
r
F (r ) dr = −
∞
mα
3r 3
tomando como referencia una energía potencial nula en el infinito. Por tanto, la energía
queda expresada en la forma
1 2
L2
mα
E = mr& +
− 3
2
2
2mr
3r
• Para determinar la trayectoria radial de la partícula, despejamos la velocidad
radial
dr
2E
L2
2α
r& =
=−
− 2 2+ 3
dt
m mr
3r
tomando el signo menos por ser la velocidad radial negativa (el radio vector decrece en
el tiempo). Integrando, el tiempo de caída sobre O es
T =−
∫
0
a
dr
=
2E
2α
L2
−
+
m m 2r 2 3r 3
∫
a
0
dr
2E
2α
L2
− 2 2+ 3
m mr
3r
Este tiempo puede calcularse una vez determinado el momento angular respecto a O y
el valor de la energía de la partícula.
• Por ser la fuerza una fuerza central, se conserva el momento angular respecto a
O. Calculamos su valor tomando como referencia el momento inicial del movimiento
L = ma
2α
2α
3 =m
3a
3a
Además, se conserva la energía. Inicialmente
1
m 2 2α mα
2
E = m⋅0 +
−
=0
2
2ma 2 3a 3a 3
Por tanto, el tiempo de caída está dado por la integral
T=
∫
a
dr
2α
2α
3 −
3r
3ar 2
0
• Con el cambio de variable
=
3
2α
∫
a
0
r dr
1 1
−
r a
r = aω
obtenemos
T =a
3a
2α
2
La integral indefinida tiene la solución
con lo cual
∫
∫
ω 3 / 2 dω
1−ω
0
1
ω 3 / 2 dω
3 ω 3
= − ω (1 − ω )  +  + arcsin ω
1− ω
4 2  4
∫
ω 3 / 2 dω 3
3π
= arcsin 1 =
4
8
1−ω
0
1
Finalmente, el tiempo de caída resulta ser
27 a 5
T =π
128 α
2.9 Se somete a una partícula de masa m a una fuerza central
r
k r
F = − 2 ur , k > 0 . Calcular su trayectoria. ¿Cuál debe ser su velocidad inicial
r
para que dicha trayectoria sea una circunferencia de radio r0 y centro O?
• En función de la variable u, la fuerza que sufre la partícula es
1
F   = − ku 2
u
y la 2ª fórmula de Binet nos dice que la órbita
r=
1
u (φ )
es solución de la ecuación diferencial
u′′ + u = −
m  1  mk
F  =
L u 2  u  L2
2
• La solución es suma de la solución general de la ecuación homogénea
u′′ + u = 0 , esto es, u g = A cos(φ − φ0 ) , y una solución particular de la ecuación
completa. Elegimos esta solución particular como la solución constante, u p =
mk
. Por
L2
tanto,
u = ug + u p =
mk
+ A cos(φ − φ0 )
L2
De aquí, la órbita queda definida por
r=
p
1 + e cos(φ − φ0 )
ecuación de una cónica de parámetro p
p=
mk
L2
y excentricidad e
AL2
mk
El ángulo φ 0 es el formado por el eje polar φ = 0 , y el eje x.
e=
• La trayectoria será un circunferencia de radio r0 si e = 0 , y si p = r0 . Por tanto
r0 =
mk
L2
Por ser la fuerza central, el momento angular respecto a O se conserva. Inicialmente la
partícula lleva una velocidad V0 perpendicular al radio vector r0 , por lo que
L = mr0V0
La velocidad necesaria para la órbita circular es
m 2r02V02
r0 =
mk
k
V0 =
mr0
Además se comprueba que en la órbita circular hay un equilibrio de las fuerzas
radiales. La fuerza central debe anularse con la fuerza centrífuga debida al giro respecto
aO
k
V02
=m
r0
r02
2.10 Una partícula se mueve en una órbita circular de radio a, bajo la acción de
una fuerza central dirigida hacia un punto O. Sean Vmax ,Vmin los valores máximo y
mínimo de su velocidad. Calcular el período de la órbita en función de estos datos.
m
Vmax
rmin
rmax
O
Vmin
a
• En el caso más general, la órbita circular no tiene por qué estar centrada en O.
Tomando coordenadas polares con centro en O, la órbita es una elipse. Al ser la fuerza
central, el momento angular respecto a O es constante. En los puntos donde la
velocidad es máxima o mínima, el vector velocidad no tiene componente radial, y es
perpendicular al radio vector. Por tanto, el momento angular satisface
L = mrmaxVmin = mrminVmax
• Además, ya que los puntos de velocidad máxima y mínima se encuentran en
posiciones opuestas sobre la circunferencia de radio a
rmin + rmax = 2a
Utilizando esta expresión junto con la ecuación anterior obtenemos el momento angular
en función de los datos del problema
L = 2ma
VmaxVmin
Vmax + Vmin
• Como la fuerza es central, se satisface la ley de las áreas. Si T es el período de
2
revolución en la órbita circular de radio a, cuyo radio vector barre una superficie π a
tenemos
πa 2
L
=
T
2m
De aquí, podemos calcular, conocido el momento angular, el período de la órbita
T = πa
Vmax + Vmin
VmaxVmin
Problemas Propuestos
2.11 Una partícula de masa m se mueve bajo el efecto de una fuerza central de
modo que el ángulo α que forma el vector velocidad y el radio vector es constante.
Calcular su trayectoria y el tiempo que tarda en caer al origen si parte de la
r r
r
posición r = r0 en t = 0 , con velocidad v 0 .
(Para integrar la ecuación del movimiento no hace falta conocer la forma exacta de la
fuerza central)
r 2 = r02 − cosα r0 v0t


Solución: φ = φ0 − tan α ln 1 − cosα
T=
v0t 
r0 
r0
v0 cosα
2.12 Una partícula de masa m sometida a la fuerza central F (r ) = −
k
,k >0
r2
sigue una trayectoria circular de radio r0 . Determinar su energía, momento
angular y velocidad.
Solución: E = −
1k
k
, L = mkr0 , v =
2 r0
mr0
2.13 Una partícula se mueve con velocidad constante v a lo largo de una línea
recta que dista b del origen O. Sea dA el área barrida en el tiempo dt por el vector
de posición que va desde O a la partícula. Demostrar que dA/dt es constante en el
tiempo e igual a L/2m, donde L es el momento angular de la partícula respecto al
origen O.