MC2416 - Métodos Aproximados

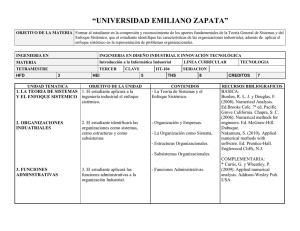
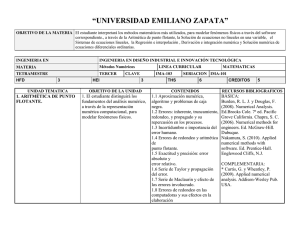
UNIVERSIDAD SIMON BOLIVAR
DIVISION
FISICA Y MATEMATICAS
DEPARTAMENTO
MECANICA
ASIGNATURA
MC 2416
METODOS APROXIMADOS
HORAS / SEMANA
T=3
P=2
VIGENCIA
SEPTIEMBRE 1991 -
L=0
U=3
APROBACION:
OBJETIVOS GENERALES
Comprender y aplicar los diferentes métodos numéricos para la resolución aproximada de problemas de
ingeniería mecánica con sus respectivos análisis de errores o criterios de convergencia y estabilidad,
según el caso.
PROGRAMA
1
Solución de ecuaciones no lineales
Método de la bisección del intervalo (Bolzano). Método de interpolación lineal. Método de
interpolación lineal modificado. Métodos de segundo orden cerrados. Método del punto fijo.
Aceleración de Aitken. Método de la secante. Método de Newton - Raphson. Método de Newton
relajado. Método de raíces múltiples. Método de Newton modificado. Métodos de segundo
orden abiertos. Método de Bairstow. Criterios de convergencia y análisis de errores
.
2
Solución de sistemas de ecuaciones
Sistemas de ecuaciones lineales. Método de eliminación simple. Estrategias de normalización
(por fila, global) y pivote (parcial, total). Método de Gauss y Gauss-Jordan. Descomposición L-U
de una matriz (Choleski, Doolittle). Sistema tridiagonal (Algoritmo de Thomas - TDMA).
Determinante de una matriz. Matriz inversa. Norma de vectores y matrices: máxima fila o
columna, euclideana, espectral. Condicionamiento de un sistema de ecuaciones lineales. Método
de Jacobi y método de Gauss- Seidel. Método de relajación sucesiva. Métodos para el cálculo de
autovalores y autovectores. (directos e iterativos).
Sistemas de ecuaciones no lineales. Método del punto fijo. Método de Newton-Raphson. Método
de Newton relajado. Método de cuasi-Newton (Broyder). Método de mínimos cuadrados.
Métodos de segundo orden. Criterios de convergencia y análisis de errores.
3
Interpolación y aproximación
Interpolación para datos irregulares. Polinomios de Newton de diferencias divididas. Polinomios
de Lagrange. Interpolación para datos regulares (diagramas romboidales). Polinomio
de
Newton-Gregory. Polinomio de Stirling. Polinomio de Bessel. Polinomio de Gauss. Métodos de
mínimos cuadrados (lineal y no lineal). Trazadores rectilíneos, parabólicos y cúbicos. Análisis de
Errores.
4
Derivación e integración numérica
Derivación para datos no regulares. Derivación numérica para datos regulares. Diagramas
romboidales. Integración para datos no regulares. Fórmulas de Newton-Cotes. (Fórmulas de:
trapecio, Simpson 1/3, Simpson 3/8, Villaceau, Hardy). Extrapolación de Richardson. Fórmula de
Romberg. Cuadratura de Gauss-Legendre. Integrales múltiples: dobles, triples, etc. Análisis de
Errores.
5
Solución de ecuaciones diferenciales ordinarias
Método de Taylor. Métodos de Runge-Kutta. Métodos predictor-corrector. Método del disparo.
Diferencias finitas. Ecuaciones diferenciales de orden superior. Sistemas de ecuaciones
diferenciales. Análisis de errores y estabilidad
BIBLIOGRAFIA
[1]
[2]
[3]
Nakamura, S. Métodos Numéricos Aplicados con Software, Prentice - Hall, 1992.
Gerald, C.F. Análisis Numérico, 2da Edición. Ediciones Alfaomega, 1991.
Burden, R.L. y Faires, J.D. Análisis Numérico, 3ra Edición. Grupo Editorial Iberoamericana,
1985.
[4] Conte, S.D. y Carl de Boor. Análisis Numérico, 2da Edición. McGraw - Hill, 1974.
[5] Chapra, S.C. y Canale, R.P. Numerical Methods for Engineers, 2nd Edition, McGraw - Hill,
1988.
[6] Ralston, A. y Rabinowitz, P. A First Course in Numerical Analysis, 2nd Edition. McGraw - Hill,
1978.
[7] Press, W.H., Flannery, B.P., Teukolsky, S.A. y Vetterling, W.T. Numerical Recipes: The Art of
Scientific Computing, Cambridge University Press, 1986. 4th Printing, 1988.
[8] Carnahan, B., Luther, H.A. y Wilkes, J.O. Applied Numerical Methods. John Wiley & Sons,
1969.
[9] Scheid, F. y Di Costanzo, R.E. Métodos Numéricos, 2da Edición. McGraw - Hill, 1991.
[10] Hamming, R.W. Numerical Methods for Scientists and Engineers, 2nd Edition. Dover
Publications, 1973. 2nd Printing 1986.
[11] Pachner, J. Handbook of Numerical Analysis Applications, McGraw - Hill, 1984.
MC2416 - Métodos Aproximados / Pág. 2 de 3
[12]
[13]
[14]
[15]
Atkinson, K.E. An Introduction to Numerical Analysis, 2nd Edition. John Wiley & Sons, 1989.
Isaacson, E. y Keller, H.B. Analysis of Numerical Methods, John Wiley & Sons, 1966.
Dahlquist, G. y Björck, Å. Numerical Methods, Prentice - Hall, 1974.
Szidarovszky, F. y Yakowitz, S. Principles and Procedures of Numerical Analysis, Plenum Press,
1978.
[16] Stoer, J. y Bulirsch, R. Introduction to Numerical Analysis, Springer - Verlag, 1980.
MC2416 - Métodos Aproximados / Pág. 3 de 3