efecto de la temperatura en el
Anuncio
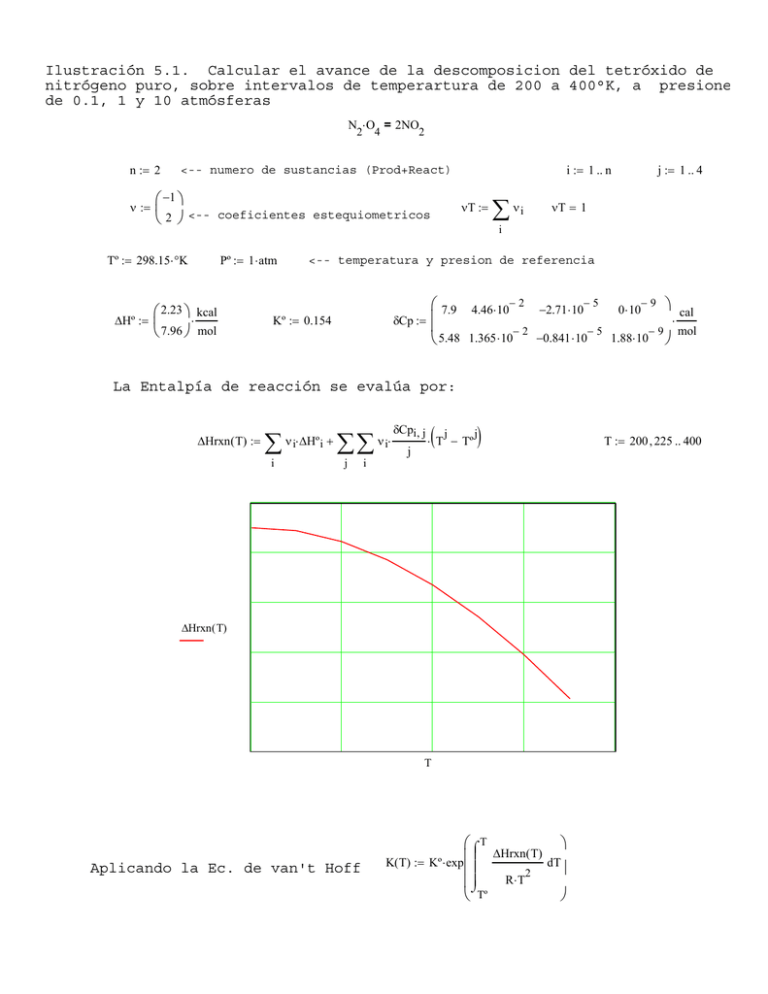
Ilustración 5.1. Calcular el avance de la descomposicion del tetróxido de nitrógeno puro, sobre intervalos de temperartura de 200 a 400°K, a presione de 0.1, 1 y 10 atmósferas N ⋅ O = 2NO 2 n := 2 ν := 2 i := 1 .. n <-- numero de sustancias (Prod+React) ⎛ −1 ⎞ ⎜ ⎝ 2 ⎠ <-- coeficientes estequiometricos Tº := 298.15⋅ °K ∆Hº := 4 Pº := 1 ⋅ atm ⎛ 2.23 ⎞ ⋅ kcal ⎜ ⎝ 7.96 ⎠ mol νT := ∑ νi j := 1 .. 4 νT = 1 i <-- temperatura y presion de referencia Kº := 0.154 δCp := ⎛ 7.9 4.46⋅ 10− 2 −2.71⋅ 10− 5 0⋅ 10− 9 ⎞ cal ⎜ ⋅ ⎜ −2 −5 − 9 mol −0.841 ⋅ 10 1.88⋅ 10 ⎠ ⎝ 5.48 1.365 ⋅ 10 La Entalpía de reacción se evalúa por: ∆Hrxn( T) := ∑ i ν i⋅ ∆Hº i + ∑∑ j ν i⋅ δCpi , j j ( j ⋅ T − Tº ) j i ∆Hrxn ( T) T Aplicando la Ec. de van't Hoff ⎛⌠ T ⎞ ⎜ ⎮ ∆Hrxn( T) d K( T) := Kº ⋅ exp ⎮ T ⎜ ⎟ 2 R⋅ T ⎜⎮ ⌡ ⎝ Tº ⎠ T := 200 , 225 .. 400 log( K( T) ) T Del balance de masa para esta reacción, podemos expresar para ε: 2 Kp = ∏ i= 1 y = i 4⋅ ε 2 1−ε 2 ⋅P ε ( T , P) := y de allí: K( T) P⋅ ⎛⎜ 4 + ⎝ K( T) ⎞ P ⎠ ⎛ 0.1 ⎞ calculando para varias presiones y temperaturas: P := ⎜ 1.0 ⎜ ⎝ 10 ⎠ T := 200 , 210 .. 400 ε ( T , P 1) ε ( T , P 2) ε ( T , P 3) T BIBLIOGRAFIA Sandler, Stanley I. (1999). "Chemical and Engineering Thermodynamics". Third Edition. John Wiley & Sons. New York. Ing. Federico G. Salazar
![orden 0 t(s) []](http://s2.studylib.es/store/data/007981523_1-258a35373fd4111c6f98c056565434ee-300x300.png)
