Trigonometric Identities MTH 151 Reciprocal Identities csc t = 1 sin t

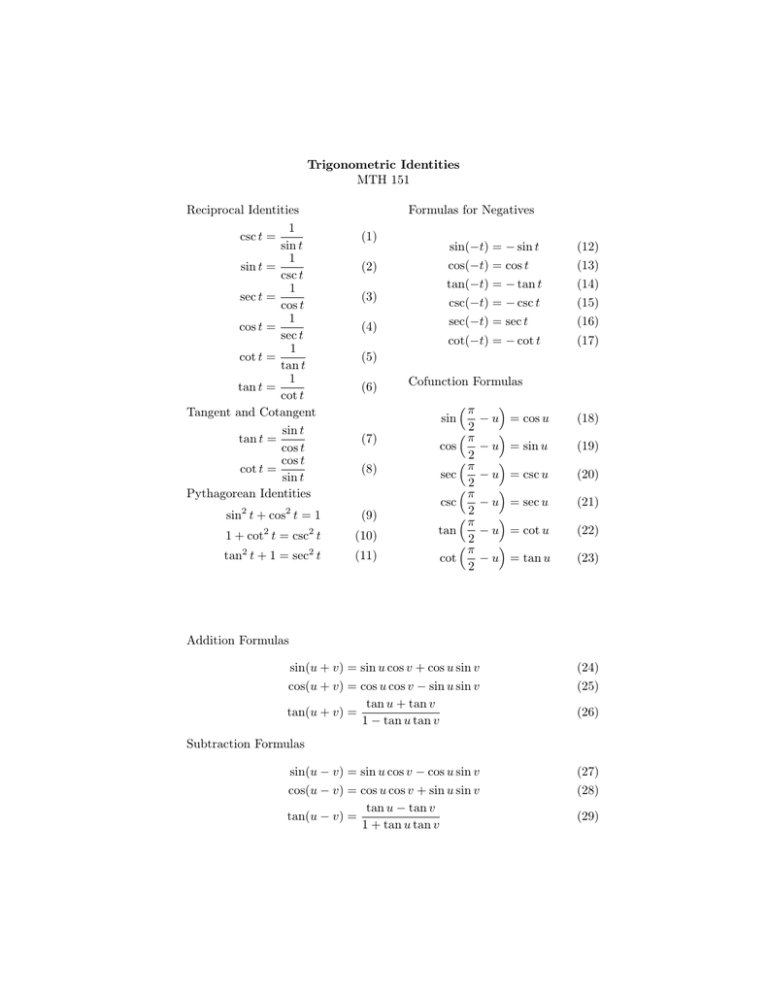
Trigonometric Identities
MTH 151
Reciprocal Identities
1
csc t =
sin t
1
sin t =
csc t
1
sec t =
cos t
1
cos t =
sec t
1
cot t =
tan t
1
tan t =
cot t
Tangent and Cotangent
sin t
tan t =
cos t
cos t
cot t =
sin t
Pythagorean Identities
Formulas for Negatives
(1)
(2)
sin(−t) = − sin t
(12)
cos(−t) = cos t
(13)
tan(−t) = − tan t
(14)
(3)
csc(−t) = − csc t
(15)
(4)
sec(−t) = sec t
(16)
cot(−t) = − cot t
(17)
(5)
(6)
Cofunction Formulas
sin
(7)
(8)
cos
sec
csc
sin2 t + cos2 t = 1
(9)
1 + cot2 t = csc2 t
(10)
tan
tan2 t + 1 = sec2 t
(11)
cot
π
2
π
2
π
2
π
2
π
2
π
2
− u = cos u
− u = sin u
− u = csc u
− u = sec u
− u = cot u
− u = tan u
(18)
(19)
(20)
(21)
(22)
(23)
Addition Formulas
sin(u + v) = sin u cos v + cos u sin v
(24)
cos(u + v) = cos u cos v − sin u sin v
tan u + tan v
tan(u + v) =
1 − tan u tan v
(25)
(26)
Subtraction Formulas
sin(u − v) = sin u cos v − cos u sin v
(27)
cos(u − v) = cos u cos v + sin u sin v
tan u − tan v
tan(u − v) =
1 + tan u tan v
(28)
(29)
Double-Angle Formulas
sin 2u = 2 sin u cos u
(30)
2
2
Half-Angle Formulas
cos 2u = cos u − sin u
2
cos 2u = 1 − 2 sin u
2
cos 2u = 2 cos u − 1
2 tan u
tan 2u =
1 − tan2 u
Half-Angle Identities
1 − cos 2u
sin2 u =
2
1 + cos 2u
2
cos u =
2
1 − cos 2u
2
tan u =
1 + cos 2u
(31)
(32)
(33)
(34)
r
v
1 − cos v
sin = ±
2
2
r
v
1 + cos v
cos = ±
2
2
r
v
1 − cos v
tan = ±
2
1 + cos v
(38)
(39)
(40)
(35)
Alternate Half-Angle Formulas
(36)
1 − cos v
v
=
2
sin v
v
sin v
tan =
2
1 + cos v
(37)
tan
(41)
(42)
Product-to-Sum Formulas
sin u cos v = 12 [sin(u + v) + sin(u − v)]
cos u sin v =
cos u cos v =
sin u sin v =
1
2 [sin(u + v) − sin(u − v)]
1
2 [cos(u + v) + cos(u − v)]
1
2 [cos(u − v) − cos(u + v)]
(43)
(44)
(45)
(46)
Sum-to-Product Formulas
a−b
a+b
cos
2
2
a+b
a−b
sin a − sin b = 2 cos
sin
2
2
a+b
a−b
cos a + cos b = 2 cos
cos
2
2
a+b
a−b
cos a − cos b = −2 sin
sin
2
2
sin a + sin b = 2 sin
(47)
(48)
(49)
(50)