Àlgebra linial - IES Jaume I de Borriana

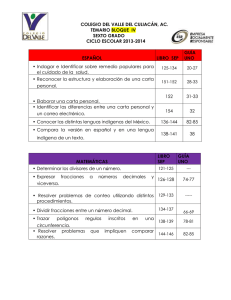
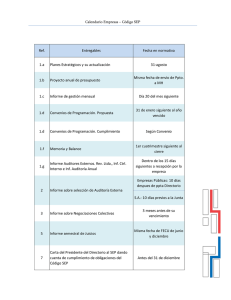
ALGEBRA LINEAL
1
Junio 99
2
Junio 99
3
Junio 99
4
Junio 99
5
Sep. 99
6
Sep. 99
7
Sep. 99
8
Sep. 99
1 2
. Aplica los
2 1
 x+ y = 2
resultados obtenidos en la resolución del sistema 
.
 2x − y = 1
Un concesionario de coches vende dos modelos, el A con el que gana
100.000 ptas. por unidad vendida, y el B con el que gana 50.000 ptas. por
unidad vendida. El número de coches x vendidos del modelo A debe
verificar que 50 ≤ x ≤ 75 . El número y de coches vendidos del modelo B ha
de ser mayor o igual que el número de coches vendidos del modelo A.
Sabiendo que el número máximo de coches que se pueden vender es de 400,
determinar cuántos coches se han de vender de cada modelo para que el
beneficio sea máximo.
Un comerciante tiene x garrafas de 10 l. de aceite cada una y y botellas de 1 l
de aceite cada una. Otro comerciante tiene y garrafas de 10 l. de aceite cada
una y x botellas de 1 l. cada una. El segundo comerciante tiene 9 litros más
que el primer comerciante. Sabiendo que los dos tienen más de 30 l. de aceite
y menos de 50 l. de aceite. Averigua razonadamente cuántos litros de aceite
tiene cada uno.
Sea el polígono de vértices (0, 0), (6, 0), (8, 3), (4, 8) y (0, 6). Calcula en que
puntos del polígono P, alcanza la función f ( x, y ) = 2 x + 3 y los valores
máximo y mínimo.
Me ofrecen la posibilidad de comprar hasta 6 millones de acciones de la
compañía A, que producen un beneficio de un 30 %, y hasta 10 millones de
acciones de la compañía B, que producen un 20 % de beneficio. Tengo 12
millones para invertir. Razona como distribuir la inversión para maximizar el
beneficio.
Un joyero tiene tres clases de monedas A, B y C. Las monedas del tipo A
tienen 2 gramos de oro, 4 gramos de plata y 14 gramos de cobre; las del tipo
B tienen 6 gramos de oro, 4 gramos de plata y 10 gramos de cobre y las del
tipo C tienen 8 gramos de oro, 6 gramos de plata y 6 gramos de cobre.
¿Cuántas monedas de cada tipo ha de fundir para obtener 44 gramos de oro,
44 gramos de plata y 112 gramos de cobre?
Ordeno mi habitación y observo que el número de libros, revistas y discos es
60. El triple del número de discos es igual a la suma del número de libros y
del doble del número de revistas. El cuádruple del número de discos es igual
a la suma del número de libros y el triple del número de revistas. Calcula el
número de libros, revistas y discos.
Un carpintero ha de construir mesas rectangulares, las dimensiones de las
cuales no sobrepasen los dos metros, de manera que la suma de su dimensión
mayor y el doble de la menor no sobrepase los 4 metros. ¿Cuál es el máximo
valor del perímetro de estas mesas?
Calcula los determinantes
1 1
,
2 −1
2 1
,
1 −1
y
9
Junio 00
10
Junio 00
11
Junio 00
12
Junio 00
13
Sep. 00
14
Sep. 00
15
Sep. 00
16
Sep. 00
Una factoría produce coches de los modelos A y B. El beneficio por la venta
de un coche modelo A es de 450 euros, y la venta de uno del modelo B
reporta 600 euros de beneficio.
La capacidad de la factoría impide producir más de 400 coches del modelo A
por día y más de 300 coches del modelo B por día. Tampoco es posible
fabricar más de 500 coches en total cada día.
Se vende toda la producción que se hace y se quiere saber, razonadamente,
cuántos coches de cada modelo interesa fabricar para obtener el máximo
beneficio.
Por un helado, dos horchatas y cuatro batidos nos cobraron en una heladería
1.700 ptas. un día. Otro día por cuatro helados y cuatro horchatas nos
cobraron 2.200 ptas. Un tercer día tuvimos que pagar 1.300 ptas. por una
horchata y cuatro batidos. Razonar si hay o no motivo para pensar que
alguno de los días nos presentaron una factura incorrecta
Un vendedor de libros usados tiene 180 libros de la editorial A y 160 de la
editorial B, con los cuales decide hacer dos tipos de lotes, el lote económico
con tres libros de la editorial A y uno de la editorial B. Que venderá a 800
ptas. y el lote selecto con un libro la editorial A y dos de la editorial B, que
venderá a 1000 ptas. Deducir razonadamente cuántos lotes ha de hacer de
cada tipo para maximizar sus ingresos vendiendo todos los lotes.
El señor Gómez deja a sus hijos en herencia su fortuna con las siguiente
condiciones:
a) El mayor recibirá la media aritmética de lo que reciban los otros dos más
30.000 euros.
b) El mediano recibirá la media aritmética de lo que reciban los otros dos.
c) El pequeño recibirá la media aritmética de lo que perciban los otros dos
menos 30.000 euros.
Explicar, razonadamente, si esta información es suficiente para saber cuanto
ha heredado cada uno de los tres hijos.
Encuentra los máximos i mínimos de la función f ( x, y ) = 2 x + 3 y − 7 en la
región limitada por los segmentos que unen los puntos (0, 0) y (0, 6); el
punto (0, 6) y el punto (4, 4); el punto (4, 4) y el punto (6, 0); el punto (6, 0)
y el punto (0, 0).
Entre los partidos políticos A y B obtuvieron el 90 % de los votos en unas
elecciones.
Calcular el porcentaje de votos que obtuvo cada partido, sabiendo que en las
elecciones siguientes: el partido A sufrió un descenso del 10 % en el número
de votos respecto a las anteriores elecciones, el partido B tuvo un 10 % de
aumento de votantes respecto a las anteriores elecciones, y que los dos
partidos obtuvieron el 90 % del total de votos.
Encuentra las soluciones del sistema:
 x+ y+ z = 1

 y+ z = 2
− x+ y+ z = 3

Se han de comer al menos 100 grs. del alimento A. De otro alimento B se
han de comer más grs. que del alimento A. Entre los alimentos A y B no se
ha de sobrepasar los 300 grs. El producto A tiene 50 calorías/gr. ¿Cuántos
grs. se han de comer de A y cuántos de B para obtener el máximo de
calorías?
17
Junio 01
18
Junio 01
19
Junio 01
20
Junio 01
21
Sep. 01
22
Sep. 01
23
Sep. 01
24
Sep. 01
1 −3 1 0
0 −3
,
,y
. Aplicar los resultados
1 2 1 4
4 2
 x − 3y = 0
obtenidos para resolver por la regla de Cramer el sistema 
 x + 2y = 4
Una fábrica produce bombillas normales a 900 ptas. la unidad y focos
halógenos a 1200 ptas. la unidad. La capacidad máxima diaria de fabricación
es de 1000 entre bombillas normales y focos halógenos, si bien no se pueden
fabricar más de 800 bombillas normales ni más de 600 focos halógenos.
Se sabe que la fábrica vende toda la producción. Razonar cuántas bombillas
normales y cuántos focos halógenos se han de producir para obtener la
máxima facturación posible y cuál sería esta.
Hemos invertido 4.000.000 de ptas. en acciones de las empresas A, B, y C.
Después de un año la empresa A repartió un beneficio del 6 % , la B del 8 %
y la C del 10 %. En total recibimos 324.826 ptas.
a) Deducir razonadamente si se puede saber o no qué invertimos en cada
empresa.
b) Deducir razonadamente que invertimos en cada empresa sabiendo que en
la empresa C invertimos el doble que en la empresa A.
Una industria fabrica bolígrafos que vende a 400 ptas. cada uno y plumas
estilográficas que vende a 1.200 ptas. cada una. Las máquinas limitan la
producción de manera que cada día no se pueden producir más de 200
bolígrafos ni más de 150 plumas y el total de la producción no puede superar
las 250 unidades. La industria vende siempre toda su producción. Deducir
razonadamente cuántos bolígrafos y plumas ha de producir al día para
maximizar el beneficio y cuál sería este.
En una reunión hay 40 personas. La suma de los hombres y de las mujeres
triplica el número de niños. El número de mujeres excede en 6 la suma del
número de hombres más el número de niños. Razonar cuántos hombres,
mujeres y niños hay.
El INSERSO ha organizado un viaje para 800 personas con cierta empresa
que dispone de 16 autobuses de 40 plazas cada uno y 20 autobuses de 50
plazas cada uno. El alquiler de un autobús pequeño cuesta 3.000 ptas. y el de
uno grande 4.000 ptas.
Calcular razonadamente cuántos autobuses de cada clase se han de contratar
para minimizar el coste y cuál sería el coste mínimo, sabiendo que la
empresa solo dispone de 18 conductores.
La función f ( x, y ) = 2 x + 3 y está definida en el polígono de vértices (0, 0),
(6, 0), (6, 8), (4, 12) y (0, 15). Determinar de forma razonada todos los
puntos en que la función alcanza un máximo. Justificar de forma razonada si
este máximo se alcanza en un solo punto o no. ¿En que punto o puntos se
alcanza el valor del máximo?
Un estudiante obtuvo un 6 en un examen de matemáticas que constaba de
tres preguntas. En la primera pregunta obtuvo una calificación igual al doble
de la calificación que obtuvo en la segunda pregunta y en la tercera pregunta
obtuvo una calificación igual a la suma de las calificaciones de las otras
preguntas. Calcular razonadamente la calificación de cada pregunta.
Calcular los determinantes
25
Junio 02
Se considera la región factible dada por el siguiente conjunto de
restricciones:
x+ y ≤ 5
x + 3y ≥ 9
x ≥ 0, y ≥ 0
Representar la región factible que determina el sistema de inecuaciones
anterior y hallar de forma razonada el punto de la región factible donde las
siguientes funciones alcanzan su máximo y su mínimo a) f(x,y)=2x+3y, b)
f(x,y)=y-x.
26
Junio 02
Un tren transporta 500 viajeros y la recaudación del importe de sus billetes
asciende a 2115 €. Calcular de forma razonada cuántos viajeros han pagado
el importe total del billete, que vale 9 €, cuántos han pagado el 20 % del
billete y cuántos el 50 % sabiendo que el número de viajeros que han pagado
el 20 % es el doble del número de viajeros que han pagado el billete entero
27
Junio 02
Se dispone de 120 refrescos de cola con cafeína y de 180 refrescos de cola
sin cafeína. Los refrescos se venden en paquetes de dos tipos. Los paquetes
de tipo A contienen tres refrescos con cafeína y tres sin cafeína, y los de tipo
B contienen dos con cafeína y cuatro sin cafeína. El vendedor gana 6 € por
cada paquete que venda de tipo A y 5 € por cada uno de los que venda de
tipo B. Calcular de forma razonada cuántos paquetes de cada tipo debe
vender para maximizar los beneficios y calcular éste.
Los tres vértices de un triángulo son A(0, 1), B(1, 2) u C(3, 0).
a) Encontrar de forma razonada la ecuación de la recta paralela al lado AB
que pasa por el punto C y
b) Hallar el punto de intersección de esta recta con la recta de ecuación
x + 3y = 2 .
28
Junio 02
29
Sep. 02
Se pretende cultivar en un terreno dos tipos de olivos: A y B. No se puede
cultivar más de 8 ha con olivos de tipo A, ni más de 10 ha con olivos del tipo
B. Cada hectárea de olivos de tipo A necesita 4 m3 de agua anuales y cada
una de tipo B, 3 m3. Se dispone anualmente de 44 m3 de agua. Cada hectárea
de tipo A requiere una inversión de 500 € y cada una de tipo B, 225 €. Se
dispone de 4500 € para realizar dicha inversión. Si cada hectárea de olivar de
tipo A y B producen, respectivamente, 500 y 300 litros anuales de aceite:
a) Obtener razonadamente las hectáreas de cada tipo de olivo que se deben
plantar para maximizar la producción de aceite.
b) Obtener la producción máxima.
30
Sep. 02
Obtener de forma razonada la matriz X, que verifica A ⋅ X = 2 B − C , siendo:
 2 1
 3 − 4
 − 2 − 7



A = 
B = 
C = 
 − 5 0
−1 1 
 13 2 
31
Sep. 02
32
Sep. 02
Una empresa fabrica dos tipos de aparatos A y B que necesitan pasar por los
talleres X e Y. En cada taller se trabajan 100 horas a la semana. Cada aparato
A requiere 3 horas del taller X y 1 hora del taller Y, y cada aparato B
necesita 1 y 2 horas respectivamente. Cada aparato A se vende a 100 € y
cada aparato B se vende a 150 €.
a) Obtener razonadamente cuántos aparatos de cada tipo se han de producir
para que los ingreso por ventas sean máximos.
b) ¿Cuál es el ingreso máximo?
Calcular de forma razonada la ecuación de la recta paralela a y=2x-3 que
pasa por el punto de intersección de y=3x-2 y 3x-2y=1.
33
Junio 03
Dada la ecuación matricial:
 3 − 2


− 2 1 
 0
1 

34
Junio 03
Una compañía fabrica y vende dos modelos de lámparas A y B. Para su
fabricación se necesita un trabajo manual de 20 minutos para el modelo A y
30 minutos para el modelo B; y un trabajo de máquina de 20 minutos para el
modelo A y de 10 minutos para el modelo B. Se dispone para el trabajo
manual de 6.000 minutos al mes y para el de máquina de 4.800 minutos al
mes. Sabiendo que el beneficio por unidad es de 15 € para el modelo A y de
10 € para el modelo B, planificar la producción mensual para obtener el
máximo beneficio y calcula este.
Debo tomar al menos 60 mgr. de vitamina A y al menos 90 mgr. de vitamina
B diariamente. En la farmacia puedo adquirir dos pastillas de marcas
diferentes X e Y. Cada pastilla de la marca X contiene 10 mgr. de vitamina A
y 15 mgr. de vitamina B y cada pastilla de la marca Y contiene 10 mgr de
cada vitamina. Además, no es conveniente tomar más de 8 pastillas diarias.
Sabiendo que el precio de cada pastilla de la marca X es 50 céntimos de euro
y que cada pastilla de marca Y cuesta 30 céntimos de euro, calcular de forma
razonada:
a) Cuántas pastillas diarias de cada marca debo tomar para que el coste sea
mínimo, y
b) Cuál es el coste mínimo.
Cinco amigos suelen tomar café juntos. El primer día tomaron 2 cafés, 2
cortados y un café con leche y debieron pagar 3 €. Al día siguiente tomaron
un café, un cortado y tres cafés con leche, por lo que pagaron 3,25 €. El
tercer día sólo acudieron cuatro de ellos y tomaron un café, dos cortados y un
café con leche, ascendiendo la cuenta a 2,45 €. Calcular de forma razonada el
precio del café, del cortado y del café con leche.
El preu del bitllet d'una línia d'autobús s'obté sumant dues quantitats, una
fixa i una altra proporcional als quilometres recorreguts. Per un bitllet entre
les poblacions A i B s'han pagat 20 € i per un billet entre les poblacions A i C
s'han pagat 32 €. Si la distancia de A a C és el doble de la distancia de A a B,
calculeu de forma raonada quant s’haurà de pagar per un billlet a una
població que dista de A la meitat que B.
35
Junio 03
36
Junio 03
37
Sep. 03
 x   − 10 

x   
 +  y  =  6 
y   

 z  3 
obtener de forma razonada los valores de x, y z.



38
Sep. 03
Una empresa disposa d'un màxim de 16.000 unitats d'un producte que pot
vendre en unitats soltes o en lots de quatre unitats. Per empaquetar un lot de
quatre unitats es necessita el triple de material que per empaquetar una unitat
solta. Si es disposa de material per empaquetar 15.000 unitats soltes, i si el
benefici que s'obté per la venda de cada unitat solta és de 2 € i de cada lot de
quatre unitats és de 7 €, calculeu de forma raonada el nombre d'unitats soltes
i de lots de quatre unitats que s'ha de preparar per maximitzar el benefici i
calculeu-ne aquest.
39
Sep. 03
Donats els punts del pla (1, 1) i (3, -2), es demana: a) trobeu de forma
raonada l'equació de la recta que passa per ambdós punts, b) deduïu si
l'esmentada recta és paral·lela o si talla la recta d'equació 3x + y = 5, i c) e
aquest últim cas, calculeu el punt de tall.
40
Sep. 03
Es pretén invertir en dos productes financers A i B. La inversió en B ha de
ser almenys de 3.000 € i no es vol invertir en A més del doble que en B. Se
suposa que A proporcionarà un benefici del 10% i B del 5%. Si es disposa de
12.000 €, calculeu de forma raonada quant s'ha d'invertir en cada producte
per maximitzar el benefici i determineu-ne aquest.
41
Juny 04
Donades les matrius
 − 4 0
 − 1 2
 ,

A = 
B = 
C=
i
 1 1
 2 0
Calculeu la matriu X que verifica l'equació AXB=2C.
42
Juny 04
43
Juny 04
44
Juny 04
 2 0


 − 1 2
Un banc disposa de 18 milions d'euros per oferir préstecs de risc alt i mitjà,
amb rendiments del 14% i 7%, respectivament. Tot sabent que s'ha de
dedicar almenys 4 milions d'euros a préstecs de risc mitjà i que els diners
invertits en alt i mitjà risc ha d'estar com a màxim a raó de 4 a 5, determineu
quant ha de dedicar-se a cadascun del tipus de préstec per maximitzar el
benefici i calculeu aquest.
Joan decideix invertir una quantitat de 12.000 € en borsa, comprant accions
de tres empreses diferents, A, B i C. Inverteix en A el doble que en B i C
juntes. Transcorregut un any, les accions de l’empresa A s'han revaloritzat un
4%, les de B un 5% i les de C han perdut un 2% del seu valor original. Com
a resultat de tot açò, Joan ha obtingut un benefici de 432,5 €. Determineu
quant va invertir Joan en cadascuna de les empreses.
Un tren de mercaderies pot arrossegar, com. a màxim, 27 vagons. En cert
viatge, transporta cotxes, i motocicletes. Per a cotxes ha de dedicar un mínim
de 12 vagons i per a motocicletes no menys de la meitat dels vagons que
dedica als cotxes. Si els ingressos de la companyia. ferroviària són de 540 €
per vagó de cotxes i 360 € per vagó de motocicletes, calculeu com s'han de
distribuir els vagons perquè el benefici d'un transport de cotxes 1
motocicletes siga màxim. i quant val aquest benefici.
45
Sep. 04
Obteniu la matriu X que verifica
AX - B = 3X,
essent:
 3 2 − 1


A= 3 0 1 
2 1 3 


 − 2


i B =  − 1
 1 


46
Sep. 04
Un fabricant produeix en dos tallers tres models diferents d'arxivadors, el A,
el B i el C. S'ha compromés a entregar 12 arxivadors del model A, 8 del B i
24 del C. Al fabricant li costa 720 € al dia el funcionament del primer taller i
960 € el del segon. El primer taller produeix diàriament 4 arxivadors del
model A, 2 del B i 4 del C, mentre que el segon produeix 2, 2 i 12
arxivadors, respectivament. Quants dies ha de treballar cada taller per a, tot
complint el contracte, aconseguir reduir al màxim els costos de
funcionament? Quin és el valor de l’esmentat cost? Quedaria algun excedent
d’algun producte als tallers? En cas afirmatiu, determineu-ne quant.
47
Sep. 04
Dos fills decideixen fer un regal de 100 € a sa mare. Com que no tenen prou
diner, compten amb l'ajuda de son pare i decideixen pagar el regal de la
següent forma: el pare paga el triple del que paguen els dos fills junts i, per
cada 2 € que paga el germà menor, el major paga 3 €. Quants diners ha de
posar cadascú?
Calculeu els punts de la regió definida per
x+ y ≥ 6
2 x + y ≤ 15
3≤ x ≤ 6
2≤ y≤ 5
48
Sep. 04
49
Juny 05
on la funció z = 3x + 2y pren els valors màxim i mínim. Calculeu els
esmentats valors.
Helena, Pere i Joan col·loquen diàriament fulls de propaganda sobre els
parabrises deis cotxes aparcats al carrer.Pere reparteix sempre el 20% del
total de la propaganda, Joan reparteix 100 fulls més que Helena i entre Pere i
Helena col·loquen 850 fulls als parabrises. Plantegeu un sistema d’equacions
que permeta esbrinar quants fulls reparteixen, respectivament, Helena, Pere i
Joan i calculeu aquests valors.
50
Juny 05
Les necessitats vitamíniques diàries d’una persona són d’un mínim de 36
mgr. de vitamina A, 28 mgr. de vitamina C i 34 mgr. de vitamina D.
Aquestes necessitats es cobreixen prenent pastilles de la marca Energic i de
la marca Vigor. Cada pastilla de la marca Energic costa 0,03 € i proporciona
2 mgr. de vitamina A, 2 mgr. de vitamina C i 8 mgr. de vitamina D. Cada
pastilla de la marca Vigor costa 0,04 € i proporciona 3 mgr. de vitamina A, 2
mgr. de vitamina C i 2 mgr. de vitamina D. Quantes pastilles de cada marca
s’han de prendre diàriament si es desitja cobrir les necessitats vitamíniques
bàsiques amb el menor cost possible? Determineu l’esmentat cost.
51
Juny 05
 2 2 1


Siga  2 3 1 la matriu dels coeficients d’un sistema d’equacions lineals i
 2 5 1


 1
 
 1 la matriu dels seus termes independents. Es demana:
 1
 
a) Escriviu les tres equacions que formen el sistema.
b) Obteniu totes les solucions del sistema.
52
Juny 05
Un venedor disposa de 350000 € per a invertir en dos tipus de microones. El
que disposa de més accessoris té un cost de 150 € reporta un benefici de 15 €
per unitat venuda, mentre que l’altre model sols proporciona un benefici d’11
€ per unitat venuda i té un cost de 100 €. Tot sabent que només es poden
emmagatzemar 3000 microones i que no es vendran més de 2000 del model
més car, determineu quants microones de cada classe es deuen comprar per a
maximitzar el benefici i calculeu aquest.
53
Sep. 05
 a b
 que verifica l’equació matricial AXB = C ,
Calculeu la matriu X = 
 0 c
sent:
 1 0
 ,
A = 
 1 1
54
Sep. 05
2 
 1

B = 
 − 1 − 3
 − 1 − 2
 .
i C = 
 − 3 − 8
Una empresa farmacèutica té en l’actualitat dues línies d’investigació, la de
medicaments antiinflamatoris no esteroides i la de ansiolítics. Desitja
invertir en la investigació com a màxim tres milions d’euros, amb la condició
de dedicar almenys 1,5 milions d’euros als ansiolítics, amb els que espera
obtindre un benefici del 10%. En canvi en la investigació sobre medicaments
antiinflamatoris, encara que es calcula un benefici del 25%, no ha d’invertir
més d’un milió d’euros. Quina quantitat ha de dedicar a cada línia
d’investigació per a maximitzar beneficis, si a més ha de dedicar als
ansiolítics almenys el doble de diners que als antiinflamatoris? Quin benefici
obtindrà d’aquesta manera l’empresa?
55
Sep. 05
Dos germans decideixen invertir 10000 € cadascun en distints productes
financers. El major va invertir una quantitat A en un producte que ha
proporcionat un benefici del 6%, una quantitat B en un altre que ha donat una
rendibilitat del 5% i la resta en un termini fix al 2% d’interès. El germà
menor va invertir eixes mateixes quantitats en altres productes que li han
proporcionat, respectivament. uns beneficis del 4, 3 i 7 %. Determineu les
quantitats A, B i C invertides si els guanys del germà major han segut 415 € i
les del xicotet 460 €.
56
Sep. 05
Representeu la regió factible donada pel sistema d’inequacions:
x+ y ≥ −1
x≤ 2
y≥ −1
x ≥ 3y −
1
2
i trobeu els punts de la regió on la funció f(x,y)= 2x+3y assoleix els valors
màxim i mínim i obtingueu tals valors.
57
Juny 06
Tres constructores inverteixen en la compra de terrenys de la forma següent:
la primera va invertir mig milió d’euros en terreny urbà 250.000 euros en
terreny industrial i 250.000 euros en terreny rústic. La segona, va invertir
125.000, 250.000 i 125.000 euros en terreny urbà industrial i rústic,
respectivament, i la tercera, 100.000, 100.000 i 200.000 euros en aquests
mateixos tipus de terreny, respectivament. Transcorregut un any, venen tots
els terrenys. La rendibilitat que obté la primera constructora és del 13,75%,
la de la segona de 1’11,25% i, finalment la de la tercera és del 10%.
Determina la rendibilitat de cada un dels tipus de terreny per separat.
58
Juny 06
Resol el següent sistema d’equacions lineals utilitzant el mètode de Cramer:
59
Juny 06
Una refineria de petroli adquireix dos tipus de cru, lleuger i pesat, a un preu
de 70 i 65 euros per barril, respectivament. Amb cada barril de cru lleuger la
refineria produeix 0,3 barrils de gasolina 95, 0,4 barrils de gasolina 98 i 0,2
barrils de gas-oil. Així mateix, amb cada barril de cru pesat produeix 0,1, 0,2
i 0,5 barrils de cada un d’aquests tres productes, respectivament. La refineria
ha de subministrar almenys 26.300 barrils de gasolina 95, 40.600 barrils de
gasolina 98 i 29.500 barrils de gas-oil. Determina quants barrils de cada tipus
de cru ha de comprar la refineria per a cobrir les seues necessitats de
producció amb un cost mínim i calcula aquest.
60
Sep. 06
 3 − 1
 i
Determina la matriu A què verifica l’equació AB + A = 2 B t on B = 
0 2 
B t representa la matriu transposada de B.
 x + y − 2z = − 6

+ z= 5
 x
 2 x − y = 11

61
Sep. 06
Una destil·leria produeix dos tipus de whisky blend mesclant només dues
maltes destil·lades distintes, A i B. El primer té un 70% de malta A i es ven a
12 €/litre, mentre que el segon té un 50% de l’esmentada malta i es ven a 16
€/litre. La disponibilitat de les maltes A i B són 132 i 90 litres,
respectivament Quants litres de cadascun dels whiskys ha de produir la
destil·leria per a maximitzar els seus ingressos, sabent que la demanda del
segon whisky mai supera a la del primer en més del 80%? Quins serien en
aquest cas els ingressos de la destil·leria?.
62
Sep. 06
En el primer curs de batxillerat d’un institut hi ha matriculats un total de 65
alumnes dividits en tres grups: A, B i C. Dinen en el centre 42 d’ells, que
corresponen a la meitat dels del grup A, les quatre cinquenes parts dels del B
i les dues terceres parts dels del C. A una eixida fora del centre van acudir les
tres quartes parts dels alumnes del grup A, tots els del B i les dues terceres
parts dels del C, sumant en total 52 estudiants. Quants alumnes hi ha en cada
grup?
63
Juny 07
Els tres models existents d’una marca d'automòbils costen 12.000, 15.000 i
22.000 euros, respectivament. Un concessionari ha ingressat 1.265.000 euros
per la venda d'automòbils d’aquesta marca. Quants cotxes ha venut de
cadascun dels models si del més barat es van vendre tants com dels altres dos
junts i del més car la tercera part dels cotxes que costen 15.000 euros?
64
Juny 07
a) Representa gràficament el conjunt de solucions del sistema determinat per
les inequacions següents:
3 y − 4x − 8 ≤ 0 ,
y ≥ − 4x + 4 , y ≥ 2 ,
x≤ 1
b) Troba els vèrtexs de la regió anterior.
c) Calcula el punt on assoleix el mínim la funció f(x,y) =3x− y en la dita
regió. Determina aquest valor mínim.
65
Juny 07
 1 2
 , calcula A ⋅ At − 5 A− 1 , sent At i A− 1 les
Donada la matriu A = 
−
1
3


matrius transposada i inversa de A ,respectivament.
Una fàbrica de fertilitzants produeix dos tipus d’adob, A i B, a partir de dues
matèries primeres M1i M2. Per a fabricar 1 tona de A fan falta 500 Kg. de
M1 i 750 Kg. de M2, mentre que les quantitats de M1 i M2 utilitzades per a
fabricar 1Tm. de B són 800 Kg. i 400 Kg., respectivament. L’empresa té
contractat un subministrament màxim de 10 Tm. de cadascuna de les
matèries primeres i ven a 1.000 € i 1.500 € cada Tm. d’adob A i B,
respectivament. Sabent que la demanda de B mai arriba a triplicar la de A,
quantes tones de cadascun dels adobs ha de fabricar per a maximitzar els
seus ingressos i quins són aquestos?
S’estan preparant dosis amb dos tipus de complements per als astronautes de
la nau Enterprise. Cada gram del complement A conté 2 unitats de
riboflavina, 3 de ferro i 2 de carbohidrats. Cada gram del complement B
conté 2 unitats de riboflavina, 1 de ferro i 4 de carbohidrats. Quants grams de
cada complement són necessaris per a produir exactament una dosi amb 12
unitats de riboflavina, 16 de ferro i 14 de carbohidrats?
66
Juny 07
67
Sep. 07
68
Sep. 07
a) Troba els vèrtexs de la regió determinada per les inequacions següents:
3 x + y ≤ 12 ,
x − 2y ≥ − 3 , y ≥
x
− 2,
2
2x + 3y ≥ 1 ,
b) Calcula els punts de la regió on la funció f(x) = 3x — 2y assoleix els valors
màxim i mínim i determina aquestos.
69
Sep. 07
Obtín totes les solucions del següent sistema d’equacions lineals:
70
Juny 08
Una immobiliària ha venut un total de 65 places de garatge en tres
urbanitzacions diferents. Els guanys obtinguts per la venda d’una plaça de
garatge en la urbanització A són de 2.000 euros, 4.000 euros per una en la
urbanització B i 6.000 per una en la urbanització C. Sabem que s’han venut
un 50% més de places en la urbanització A que en la urbanització C. Calcula
el nombre de places de garatge venudes en cada urbanització sabent que el
benefici obtingut per les venudes en la urbanització C és igual a la suma dels
beneficis obtinguts per les venudes en les urbanitzacions A i B.
71
Juny 08
Determina la matriu X que verifica l’equació AX + I = AB t , sent I la matriu
 1 1
 2 1 t
 , B = 
 i B la transposada de la matriu B.
identitat, A = 
 − 1 1
 − 1 1
72
Juny 08
a) Representa gràficament el conjunt de solucions del sistema d’inequacions:
 x+ y+ z = −1

 2x − y + z = 0
 − 2x + 7 y + z = − 4

 3 x+ 2 y ≥ 5
 x− 2 y ≥ − 1


 5 x + 4 y ≤ 16
 x − y ≤ 5
b) Determina els vèrtexs de la regió obtinguda en l’apartat anterior.
c) Calcula el punt on assoleix el mínim la funció f ( x, y ) = 3x − y en la dita
regió. Determina aquest valor mínim.
73
Sep.08
Antoni ha aconseguit 1372 euros treballant durant les vacances. Eixos diners
pot gastar-los íntegrament comprant un ordinador portàtil, una camera digital
i fent un viatge. El preu de l’ordinador portàtil excedeix en 140 euros a la
suma dels preus de la camera i del viatge. Tenint en compte que el preu d’un
segon acompanyant per al viatge és la meitat que el preu inicial, Antoni
podria invitar el seu germà al viatge en el cas que no es comprara la camera
digital i encara li quedarien 208 euros. Calcula els preus de l’ordinador, de la
camera i del viatge.
74
Sep.08
 1 3

Donada la matriu A = 
 4 2
a) Troba la seua inversa.
8 
 6
2

b) Resol l’equació XA + 5 A = 
 10 − 20 
75
Sep.08
Un cert armador es dedica a la pesca de rap i lluç. Les quotes pesqueres
imposen que les seues captures totals no excedisquen les 30 tones (Tm).
D’altra banda, la quantitat de rap com a màxim pot triplicar a la de lluç i, a
més, aquesta última no pot superar les 18 Tm. Si el preu del rap és de 15 €/kg
i el del lluç 10 €/kg, quines quantitats de cada espècie ha de pescar per a
maximitzar els seus ingressos?
76
Juny 09
Un fruiter vol liquidar 500 kg de taronges, 400 kg de pomes i 230 de peres.
Per a això prepara dues bosses de fruita d’oferta: la bossa A consta d’ 1 kg de
taronges i 2 de pomes, i la bossa B consta de 2 kg de taronges, 1 kg de pomes
i 1 kg de peres. Per cada bossa del tipus A obté un benefici de 2,5 euros, i 3
euros per cada una del tipus B. Suposant que ven totes les bosses, quantes
bosses de cada tipus ha de preparar per a maximitzar els seus guanys? Quin
és el benefici màxim?
77
Juny 09
Resol el sistema:
x+ y− z = 2

 2x + z = 3
 x + 5y − 7z = 4

Si (x,y,0) és una solució del sistema anterior, quins són els valors d’x i d’y?
78
Sep.09
Obtín totes les matrius columna
1 1

matricial AX = B, on A =  0 1
1 2

 x
 
X =  y  que siguen solucions de l’equació
 z
 
1
 1

 
− 1 i B =  − 1 . Quines d’aquestes
 0
0 
 
matrius X tenen la primera fila nul·la?
79
Sep.09
En un sondeig d’opinió s’obté que el nombre d’individus a favor d’una certa
normativa duplica la suma dels que hi estan en contra i els que no n’opinen.
El total d’entrevistats ascendeix a 360 persones i la diferència entre els que
expressen la seua opinió i els que no ho fan duplica la diferència entre el
nombre d’individus a favor i el nombre dels que hi estan en contra de la
citada normativa. Determina quants entrevistats estaven a favor de la
normativa, quants en contra i quants no hi van opinar.
80
Sep.09
Una empresa construirà dos tipus d’apartaments, un de luxe i un altre de
superluxe. El cost del model de luxe és d’l milió d’euros i del de superluxe
d’l,5 milions. Disposa per a l’operació de 60 milions d’euros. Per a evitar
riscos, es creu convenient construir almenys tants apartaments de luxe com
de superluxe i, en tot cas, no construir més de 45 apartaments de luxe.
Quants apartaments de cada tipus interessa construir a l’empresa si vol
maximitzar el nombre total d’apartaments construïts? Esgotarà el pressupost
disponible?
81
Sep.09
Atès el sistema d’inequacions següent:
x≥ −2

 x + 3y + 5 ≥ 0

 y − 4x ≥ − 6
 3y − x ≤ 4

 y − x ≤ 2
a) Representa’n gràficament el conjunt de solucions i determina’n els
vèrtexs.
b) Obtín els punts on la funció f(x,y) = 2x-3y assoleix els valors mínim i
màxim en l’esmentada regió.
82
Juny 10
En un forn mallorquí es fabriquen dos tipus d’ensaïmades, grans i xicotetes. Cada
ensaïmada gran requereix per a l’elaboració 500 g de massa i 250 g de farcit,
mentre que una xicoteta requereix 250 g de massa i 250 g de farcit. Es disposa de
20 kg de massa i 15 kg de farcit. El benefici obtingut per la venda d’una ensaïmada
gran és de 2 euros i el d’una xicoteta és d’1,5 euros.
a) Quantes ensaïmades de cada tipus ha de fabricar el forn perquè el benefici
obtingut siga màxim?
b) Quin és el benefici màxim?
83
Juny 10
Obtín la matriu X que verifica:
84
Sep.10
Un ramader disposa d’aliment concentrat i farratge per a alimentar les seues
vaques. Cada kg d’aliment concentrat conté 300 g de proteïna crua (PC), 100
g de fibra crua (FC) i 2 Mcal d’energia neta de lactància (ENL), i el seu cost
és 11 euros. D’altra banda, cada kg de farratge conté 400 g de PC, 300 g de
FC i 1 Mcal d’ENL, sent el seu cost 6,5 euros. Determina la ració alimentària
de mínim cost si sabem que cada vaca ha d’ingerir almenys 3500 g de PC,
1500 g de FC i 15 Mcal d’ENL Quin és el cost?
 1 

2 
 2
 3   2 0 − 1 
 X −   = 
  5 
2
 − 1 − 3
 2   4 − 1 3   − 3


85
Sep.10
En un cinema s’han venut en una setmana un total de 1405 entrades i la
recaptació ha sigut de 7920 euros. El preu de l’entrada normal és de 6 euros i
la del dia de l’espectador 4 euros. El preu de l’entrada per als jubilats és
sempre de 3 euros. Se sap, a més, que la recaptació de les entrades de preu
reduït és igual al 10% de la recaptació de les entrades normals. Quantes
entrades de cada tipus s’han venut?
86
Juny 11
Un comerciant ven tres tipus de rellotges, A, B i C. Els del tipus A els ven a
200 euros, els del tipus B a 500 euros i els del tipus C a 250 euros. En un mes
determinat ha venut 200 rellotges en total. Si la quantitat dels que ha venut
aquest mes de tipus B és igual als que ha venut de tipus A i tipus C
conjuntament, calcula quants n’ha venut de cada tipus si la recaptació del
mes ha sigut de 73500 euros.
87
Juny 11
. Donades les matrius:
0
 1 − 2
 1
3 1 
 , B = 
 i C = 

A = 
−1 4 
 − 2 − 1
 2 − 1
a) Calculeu la matriu inversa de la matriu C.
b) Obteniu la matriu X que verifica AX + Bt= C, sent Bt la matriu transposada
de B.
88
Sep. 11
89
Sep.11
L’amo d’una botiga de llepolies disposa de 10 paquets de pipes, 30 xiclets i
18 bombons. Decideix que per a vendre-les millor confeccionarà dos tipus de
paquets: el tipus A estarà format per un paquet de pipes, dos xicles i dos
bombons i es vendrà a 1,5 euros. El tipus B estarà format per un paquet de
pipes, quatre xicles i un bombó i es vendrà a 2 euros. Quants paquets de cada
tipus convé preparar per aconseguir els ingressos màxims? Determineu els
ingressos màxims.
Siguen les matrius
y
.
a) Calculeu
.
b) Determineu la matriu X que verifica que
matriu identitat.
, on I és la
D