Microeconomía.Producción.Parte#2

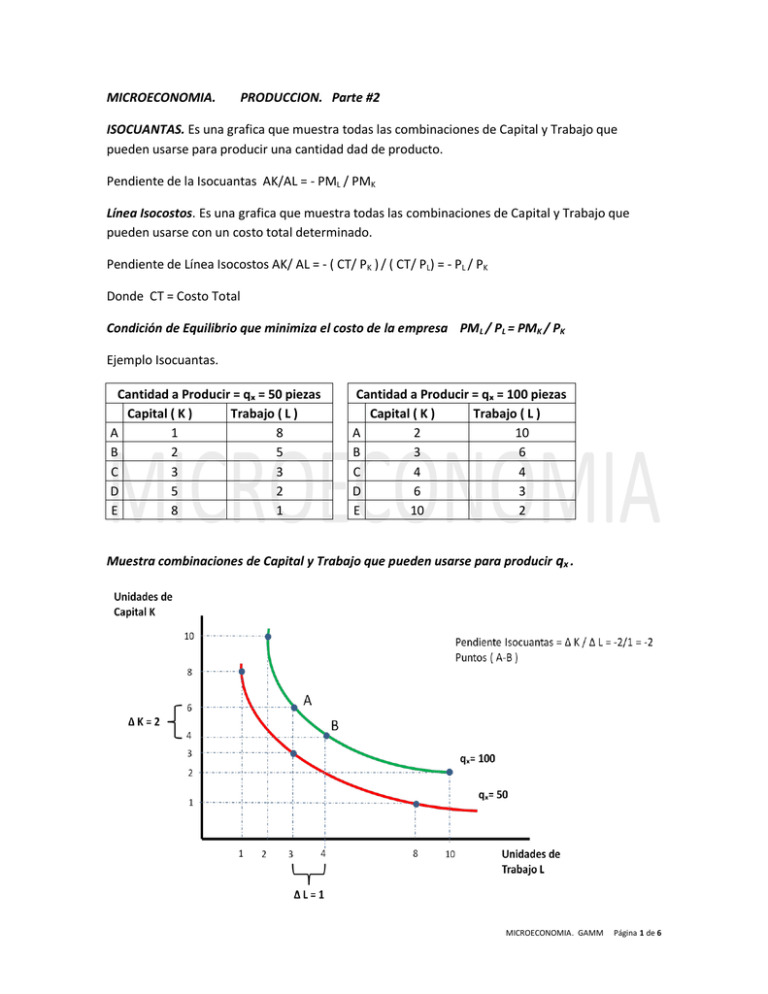
MICROECONOMIA.
PRODUCCION. Parte #2
ISOCUANTAS. Es una grafica que muestra todas las combinaciones de Capital y Trabajo que
pueden usarse para producir una cantidad dad de producto.
Pendiente de la Isocuantas AK/AL = - PML / PMK
Línea Isocostos. Es una grafica que muestra todas las combinaciones de Capital y Trabajo que
pueden usarse con un costo total determinado.
Pendiente de Línea Isocostos AK/ AL = - ( CT/ PK ) / ( CT/ PL) = - PL / PK
Donde CT = Costo Total
Condición de Equilibrio que minimiza el costo de la empresa PML / PL = PMK / PK
Ejemplo Isocuantas.
Cantidad a Producir = qₓ = 50 piezas
Capital ( K )
Trabajo ( L )
A
1
8
B
2
5
C
3
3
D
5
2
E
8
1
Cantidad a Producir = qₓ = 100 piezas
Capital ( K )
Trabajo ( L )
A
2
10
B
3
6
C
4
4
D
6
3
E
10
2
Muestra combinaciones de Capital y Trabajo que pueden usarse para producir qx .
MICROECONOMIA. GAMM
Página 1 de 6
Las graficas de Isocuantas nos muestran las combinaciones de Capital y Trabajo, para producir:
 qx= 50 piezas curva de color rojo.
 qx= 100 curva de color verde.
Línea Isocostos. Muestra todas las combinaciones de Capital y Trabajo , por Costo Total.
Supongamos un Costo Total de $25 , con Pk = $1 y PL = $5
Combinación menos costosa entre Capital y Trabajo para lograr 50 piezas de producción.
MICROECONOMIA. GAMM
Página 2 de 6
Punto
A
B
C
Capital ( K )
3
5
2
Trabajo ( L )
3
2
5
Las empresas que intentan maximizar sus beneficios podrán minimizar sus costos si producen en el
nivel de producción que hayan elegido, con la tecnología representada por el punto donde la
Isocuanta es tangente a la Línea de Isocostos.
En este caso, la tecnología que minimiza el costo ( tres unidades de Capital y tres unidades de
Trabajo ) está representada por el punto Punto A, el costo total se reduce a $6.
Como minimizar el costo de Producción.
Al graficar una serie de combinaciones de insumos para minimizar el costo, mostradas en la grafica
como los puntos A,B,C, se obtiene una grafica como la siguiente :
MICROECONOMIA. GAMM
Página 3 de 6
Una curva de costos muestra el costo mínimo para producir cada nivel de producción.
Tasa Marginal de Sustitución (Relación Marginal de Sustitución Técnica).
Es la tasa a la cual una empresa puede sustituir trabajo por capital, manteniendo constante su
producción. Expresada por PML / PMK .
Indica las proporciones en las que puede sustituirse trabajo por capital de manera que la
producción permanezca constante.
Específicamente indica el número de unidades de capital necesarias para sustituir una unidad de
trabajo.
En este ejemplo, entre los puntos A y B existe una pendiente ( negativa ), la cual nos indica
numéricamente que RMST = - ΔK / ΔL = PML / PMK :
RMST = - ΔK / ΔL = -2 / 1 = -2
2
Indica el número de
unidades de K (Capital)
para sustituir unidades de
L (Trabajo).
MICROECONOMIA. GAMM
Página 4 de 6
Rendimientos a Escala. Es la tasa a la que aumenta la producción cuando se incrementa la escala.
Escala ( Planta Optima ). Magnitud de una planta que permite minimizar los costos.
Modificación de la Escala. Aumento de todos los factores en la misma proporción:
L,K
2L , 2K
Rendimientos Crecientes a Escala. Cuando hay un incremento de la escala de producción de una
empresa, el resultado son costos medios más bajos por cada unidad producida.
F ( rL, rK ) > r F ( L, K )
Rendimientos Constantes a Escala. Un incremento en la escala de producción no tiene efecto
sobre los costos medios por unidad producida.
F ( rL, rK ) = r F ( L, K )
MICROECONOMIA. GAMM
Página 5 de 6
Rendimientos Decrecientes a Escala. Cuando hay un incremento en la escala de producción de
una empresa, el resultado son costos medios más altos por cada unidad producida.
F ( rL, rK ) < r F ( L, K )
Fuente de la información : Principios de Microeconomía. Case/Fair. Ed. Prentice Hall. Cuarta Edición.
MICROECONOMIA. GAMM
Página 6 de 6