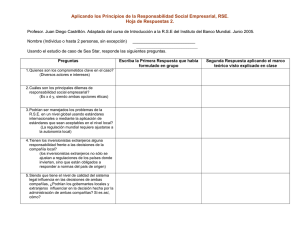
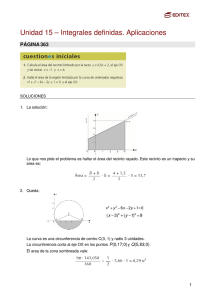
ε ρ ε ρ σ

Tecnun – Electricidad y Magnetismo: Problema 2.36
Como nos piden calcular el campo eléctrico en todo el espacio y el dato que tenemos es la distribución de carga ρ,
podemos resolver el problema aplicando el teorema de Gauss (puesto que tenemos simetría en las coordenadas φ y ϕ)
r ρ
. Lo resolvemos utilizando el segundo método, invitando a comprobar que se
o utilizando la expresión divE =
ε0
obtiene el mismo resultado aplicando Gauss.
Dividimos el espacio en tres zonas.
0<r<a
r ρ1
divE =
ε0
A)
Empleamos la expresión de la divergencia en coordenadas cilíndricas:
∂(rE r ) ρ1 ⋅ r
1 ∂ (rE r ) ρ1
=
⇒
=
=>
r ∂r
ε0
∂r
ε0
ρ1 ⋅ r 2
ρ ⋅r C
rE r =
+ C1 → E r = 1 + 1
2ε 0
2ε 0
r
Tenemos que obtener el valor de la constante de integración aplicando las condiciones de contorno. Como el campo
eléctrico está creado por una distribución volumétrica de carga, debe tener un valor finito en todo el espacio.
En r = 0:
ρ ⋅r
C
ρ ⋅r
E(0) = 1 ⇒ C1 = 0 ⇒ E r = 1
=> E = 1 u r
2ε 0
0
2ε 0
a<r <b
r ρ2
divE =
.
ε0
B)
ρ2 ⋅ r C2
+
2ε 0
r
En este caso, obtenemos el valor de C2 aplicando la continuidad del campo eléctrico en r = a.
ρ ⋅a ρ ⋅a C
a (ρ1 − ρ 2 )
No hay σ ⇒ E a + = E a − ⇒ 1 = 2 + 2 → C 2 = a ⋅
2ε 0
2ε 0
a
2ε 0
Análogamente a la zona anterior: E r =
Er =
ρ ⋅ r a 2 (ρ1 − ρ 2 )
ρ 2 ⋅ r a 2 (ρ1 − ρ 2 )
ur
+
=> E = 2 +
2ε 0
2ε 0 r
2ε 0
2ε 0 r
C) r > b
r
divE = 0
C
∂ (rE r )
1 ∂ (rE r )
=0→
= 0 → rE r = C 3 → E r = 3
∂r
r ∂r
r
Al igual que en la zona anterior, obtenemos el valor de la constante de integración aplicando la continuidad del
campo eléctrico en r = c, puesto que no hay ninguna densidad superficial de carga.
σ = 0 → E b + = Eb −
C 3 ρ 2 ⋅ b a 2 (ρ1 − ρ 2 )
ρ ⋅ b 2 a 2 (ρ1 − ρ 2 )
→ C3 = 2
+
=
+
b
2ε 0
2ε 0 b
2ε 0
2ε 0
Er =
ρ b 2 + (ρ1 − ρ 2 )a 2
ρ 2 b 2 + (ρ1 − ρ 2 )a 2
ur
= >E = 2
2ε 0 r
2ε 0 r