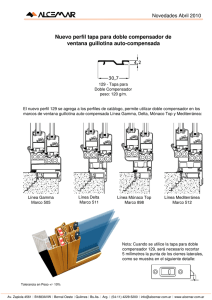
Tipos de Compensación Tipos de compensadores

- CONTROL DE PROCESOS
(segundo cuatrimestre)
- CONTROL AVANZADO y
AUTOMATISMO
Facultad de Ingeniería – UNER
Carrera: Bioingeniería
Planes de estudios: 1993 y 2008
Tipos de Compensación
+
Gc(s)
+
-
Gp(s)
-
G1(s)
+
-
Gp(s)
Gc(s)
H(s)
H(s)
Compensación en serie
Compensación en paralelo o de
retroalimenación
La elección entre una y otra depende de la naturaleza de las señales del
sistema, niveles de potencia en los diversos puntos, los componentes
disponibles, la experiencia del diseñador con el sistema, las
consideraciones económicas, etc.
Tipos de compensadores
y
Atraso o retardo de Fase:
Gc ( s) = K c β
y
Adelanto de Fase:
s+
1
τs + 1
τ
= Kc
1
βτs + 1
s+
βτ
β >1
1
Gc ( s ) = K cα
y
Atraso - Adelanto
s+
τs + 1
τ
= Kc
1
ατs + 1
s+
ατ
Teoria 2 de Control - Bioingeniería UNER
0 <α <1
1
Circuito de un Compensador
T .s + 1
E ( s ) R 2.R 4 ( R1.C1.s + 1)
=
=Kβ
β .T .s + 1
E ( s ) R1.R3 ( R 2.C 2.s + 1)
o
c
i
R 4.C1
R3.C 2
T = R1.C1
β .T = R 2.C 2
K =
c
R1.C1 < R 2.C 2 ⇒ Comp. ATRASO
R1.C1 > R 2.C 2 ⇒ Comp. ADELANTO
Compensación utilizando
Métodos de Respuesta en
Frecuencia
Compensación en adelanto
Se utiliza el compensador en adelanto siguiente
1
Gc ( s ) = K cα
s+
τs + 1
τ
= Kc
1
ατs + 1
s+
ατ
0 <α <1
donde alfa es el factor de atenuación y Kc es la ganancia del
compensador adelanto. El diagrama polar del compensador
es:
G c ( j ω ) = K cα
jωτ + 1
j ωατ + 1
ωm
1
(1 − α )
2
ω=0
α
1
(1 + α )
2
Teoria 2 de Control - Bioingeniería UNER
θm
ω→∞
1
2
sen θ m =
El ángulo de fase máximo es:
1−α
1+α
El diagrama de Bode del compensador, para τ = 1, α = 0.1 es
dB 10
0
− 10
− 20
90º
0º
0.1
1
100ω →
10
10
El ángulo máximo del compensador ocurre en la frecuencia
media entre polo y cero:
log ω m =
1
1 ⎞
1⎛
⎜ log + log
⎟
τ
ατ ⎠
2⎝
ωm =
1
ατ
Técnicas de compensación en adelanto
1) Suponga el compensador en adelanto
Gc (s ) = K cα
τs + 1
ατs + 1
defina K = K cα
El compensador y la planta en lazo abierto quedan
Gc (s )G (s ) =
τs + 1
KG (s )
ατs + 1
Determine la ganancia K que satisfaga el requisito de
constante estática de error propuesta
2) Dibuje el diagrama de Bode K.G(s).H(s)
3) Determine el ángulo de fase que se necesita agregar al
sistema. A ese valor, agréguele de 5º a 12º más (por el
desplazamiento de la magnitud).
4) Con el ángulo deseado, determine el factor de atenuación
senθm =
1−α
1+ α
después determine la frecuencia donde la magnitud del
sistema no compensado sea:
1
− 20log⎛⎜ ⎞⎟
⎝ α⎠
Teoria 2 de Control - Bioingeniería UNER
3
Esta frecuencia es la nueva frecuencia de cruce de ganancia.
Utilizando esta frecuencia la ecuación
ωm =
1
se obtiene el valor del cero
1
ατ
y del polo
τ
1
ατ
5) Con K y α , calcule la constante del compensador
Kc =
K
α
6)Verifique el margen de ganancia del sistema compensado.
Ejemplo: Dado G(s) diseñe un compensador en adelanto que
haga que el error en estado estable ante una rampa sea de
0,05. Al mismo tiempo, el margen de fase sea mayor a 45°.
G(s) =
7 .5
s( s + 3)
Solución:
1) Se supone un compensador en adelanto de la forma
Gc ( s ) = K cα
jωτ + 1
jωατ + 1
se define K = K cα
2) Se encuentra la ganancia K que junto con el sistema
cumplan con la constante de error estático de velocidad.
Kv = limsGc (s)G(s) = lim
s→0
τs +1
s→0 ατs +1
KG(s) = lim
s7.5K
s→0 s(s + 3)
= 2.5K = 20
K =8
3) Se realiza el diagrama de Bode del sistema a compensar
con la ganancia K:
60
KG ( s) =
s ( s + 3)
Teoria 2 de Control - Bioingeniería UNER
4
4) Del diagrama de Bode, observe el margen de fase y
determine el adelanto de fase que se requiere agregar:
M f = 21.9°
M f deseado = 45°
φm = M f deseado − M f + 5°
φm = 28.1° ≈ 28°
5) De
φmse obtiene α
sen θ m =
1−α
1+α
α = 0.361
6) Ahora se calcula el cambio de magnitud que se obtiene al
agregar el compensador. Se utiliza:
20 log(1 / α )
20 log(1 / 0.361) = 4.4249
se observa en el diagrama de Bode en qué frecuencia se tiene
una magnitud de − 20 log(1 / α )
y se define como la nueva
frecuencia de cruce de ganancia.
ωc = 9.77 rad / seg.
El máximo aporte de fase del compensador debe ocurrir
en wm:
ωm =
1
ατ
= ωc
7) Se obtiene el cero y el polo del compensador
cero 1 = α ωc = 5.88
polo
τ
1
ατ
=
ωc
= 16.24
α
8) Con α y K se obtiene la ganancia del compensador
Kc =
K
α
= 22,3
y el compensador es
Gc ( s ) = 8 *
s + 5,88
0,17.s + 1
= 22,3
s + 16,24
0,061.s + 1
Teoria 2 de Control - Bioingeniería UNER
5
Gc
Gc G
G
Gc
GcG
M f = 45.1°
a 9.77 rad / seg
G
PARA PENSAR: ¿Cómo diseño un compensador en
adelanto si el requisito de diseño es un error estático y
el MARGEN de GANANCIA?
Ejemplo: Dado G(s) diseñe un compensador en adelanto que
logre un error de posición (offset) menor al 5% y un margen de
ganancia superior a 6[dB]. El Margen de ganancia es el
requisito de diseño.
G(s) =
20
( s + 1) .( s + 5).( s + 10)
Compensación en atraso
1
Gc ( s ) = K c β
el valor del polo −
1
s+
τs + 1
τ
= Kc
1
βτs + 1
s+
βτ
β >1
es más positivo que el del cero −
βτ
1
τ
.
El diagrama polar del compensador en retraso es
Im
Kc
ω→∞
Kcβ
ω=0
Teoria 2 de Control - Bioingeniería UNER
Re
6
El diagrama de Bode es el siguiente:
dB
20
β =10
τ =1
Kc =1
10
0
0º
− 90 º
0.01
0 .1
10 ω →
1
El valor más negativo de la fase se encuentra entre las
frecuencias asociadas al polo y al cero. Mientras que la
magnitud total disminuye en 20 dB.
Técnicas de compensación en atraso
1) Suponga el compensador en atraso
Gc ( s ) = K c β
se define K = K c β
1
s+
τs + 1
τ
= Kc
1
βτs + 1
s+
βτ
β >1
y el sistema compensado es
Gc ( s )G ( s ) =
τs + 1
KG ( s )
βτs + 1
2) Determine la ganancia K que satisfaga el requisito de
constante estática de error propuesta
3) Dibuje el diagrama de Bode del sistema sin compensar con
la ganancia K calculada en el punto anterior.
4) Si no cumple con los requisitos de margen de fase
deseados. Entonces encuentre la frecuencia donde el ángulo
de la fase es -180º más el margen de fase requerido, más
unos 5 o 12 grados.
5) Seleccione esta frecuencia como la nueva frecuencia de
cruce de la ganancia.
6) Seleccione la nueva frecuencia de corte del cero (1/T) una
década mas chica que la nueva frecuencia de cruce de la
ganancia, obtenida en el paso 5. Esto se hace para alejar de
la frecuencia de cruce, los efectos del atraso de fase.
7) Determine la atenuación necesaria para llevar la curva de
magnitud a cero dB, en la nueva frecuencia de cruce. Con
esta atenuación se determina el valor de β .
dB = −20 log β
Teoria 2 de Control - Bioingeniería UNER
7
β y el cero, se obtiene la frecuencia de
8) Con el valor de
corte del polo
1
βτ
9) Por último se obtiene la ganancia del compensador:
Kc =
K
β
Ejemplo: Compense por atraso el siguiente sistema:
G(s) =
2
s ( s + 1)( s + 2)
de forma tal que la constante de error estático de velocidad
−1
sea de 5 seg , el margen de fase sea al menos de 40° y el
margen de ganancia al menos de 10dB.
.
Solución:
1) Se utiliza un compensador en atraso de la forma
Gc ( s ) = K c β
se define
τs + 1
βτs + 1
K = Kc β
2) Ajustar la ganancia K para que junto al sistema cumpla con
las especificaciones de error estático de velocidad.
K v = lim s
s →0
2
τs + 1
=5
KG ( s ) = lim sK
s →0
βτs + 1
s ( s + 1)( s + 2)
K =5
3) Se realiza el diagrama de Bode del sistema a compensar con
la ganancia K
KG ( s ) =
KG ( jω ) =
10
s ( s + 1)( s + 2)
5
jω ( jω + 1)( j 0.5ω + 1)
Teoria 2 de Control - Bioingeniería UNER
8
3)
Diagrama de Bode
4) Del diagrama de Bode, observe el margen de fase. El
sistema tiene un margen de fase de -13°, por lo que es
inestable.
Se busca el valor de frecuencia en donde se tiene un ángulo
de fase de -180°+ el margen de fase deseado + 12° de
margen de seguridad.
− 180º +40º +12 º
= −128º
5) Generalmente se coloca el cero para que tenga un
frecuencia de corte una década menor que la nueva
frecuencia de cruce de ganancia. En este caso
correspondería a 0,05 [rad/seg], pero por cuestiones de
diseño, no se recomiendan constantes de tiempo muy
grandes y se opta por asignar al cero una frecuencia de corte
de 0,1 [rad/seg]
1
τ
= 0.1
6) Lo siguiente es hacer que en la nueva frecuencia de cruce
seleccionada ( 0,47 [rad/seg] ) la magnitud pase por 0 [dB].
De la gráfica de Bode se observa que en la frecuencia de
cruce seleccionada, la magnitud es de 19.4, se aproxima a
20 [dB]:
− 20 = −20 log β
β = 10
Teoria 2 de Control - Bioingeniería UNER
9
7) Con el valor de β y el valor del cero, se obtiene el polo
1
βτ
=
1
100
8) Por último se obtiene la ganancia del compensador:
Kc =
K
β
=
5
10
El compensador en atraso queda:
Gc ( s ) = 0.5
s + 0 .1
s + 0.01
PARA
PENSAR:
¿Cómo
diseño
un
compensador de ATRASO si el requisito de
diseño es un error estático y el MARGEN de
GANANCIA?
Ejemplo: Dado G(s) diseñe un compensador de ATRASO que
logre un error de posición (offset) menor al 5% y un margen de
ganancia superior a 6[dB]. El Margen de ganancia es el
requisito de diseño.
G(s) =
20
( s + 1) .( s + 5).( s + 10)
Ejemplo: Colocar un compensador de ADELANTO en serio con
el de atraso recién diseñado para mejorar el Margen de FASE
y llevarlo a unos 45º conservando el margen de ganancia y el
error de posición anteriores. ESTO ES UN COMPENSADOR
DE ATRASO – ADELANTO!!!!
G(s) =
20
( s + 1) .( s + 5).( s + 10)
Teoria 2 de Control - Bioingeniería UNER
10