Resolución de ecuaciones no lineales Tema 3:

Tema 3:
Resolución de ecuaciones no lineales
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
Acotación y separación de raíces.
V.Álvarez
J.A. Armario
F. Muñoz
Ecuaciones polinómicas. Método de Sturm.
Método y algoritmo de la bisección: análisis de errores.
Método de Newton: convergencia del método.
Regla de Fourier.
Caso de raíces múltiples: aceleración de la convergencia
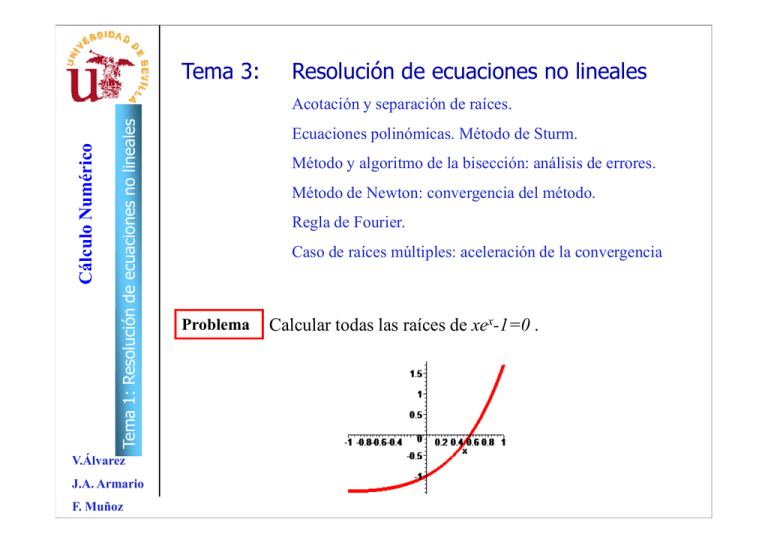
Problema
Calcular todas las raíces de xex-1=0 .
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
Solución de una ecuación no lineal
V.Álvarez
J.A. Armario
F. Muñoz
Una ecuación no lineal es una ecuación del tipo f(x)=0,
donde f(x) es una función no lineal.
Un número x es solución o raíz de la ecuación si f(x )=0. A
un tal x se le denomina también cero de la función f(x).
Una raíz
x de la ecuación f(x)=0 tiene multiplicidad n si
f ( x) = f ' ( x) = L = f n −1) ( x) = 0 y f n ) ( x) ≠ 0
Cuando n=1 se habla de raíz simple, en otro caso, múltiple.
Ejemplo: La parábola y=(x-1)2 tiene un cero doble (i.e. de
multiplicidad 2) en la abscisa x=1, mientras que la recta y=x-1
tiene un cero simple en dicho punto.
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
A) Localización y separación de las raíces
V.Álvarez
J.A. Armario
F. Muñoz
Método gráfico: a modo de orientación
Analíticamente:
Crecimiento: signo f ’(x)
Bolzano: f continua en [a,b], f(a)·f(b)<0
Sucesiones de Sturm: caso de polinomios
B) Aproximación numérica de cada una de las raíces
Bisección: si se satisface Bolzano
ewton: si se satisface Fourier
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
A) Localización y separación de las raíces
V.Álvarez
J.A. Armario
F. Muñoz
Método gráfico: a modo de orientación
x≠0
x ⋅ e −1 = 0 ⇔ ex =
x
1
x
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
A) Localización y separación de las raíces
V.Álvarez
J.A. Armario
F. Muñoz
Analíticamente:
Crecimiento: signo f ’(x)
f ' ( x) = ( x + 1)e x
e x >0
f ' ( x) = 0 ⇔ ( x + 1)e x = 0 ⇔ x + 1 = 0
-
f ' (−2) = −
1
< 0, f ↓ en (−∞,−1)
2
e
+
-1
f ' (0) = 1 > 0, f ↑ en (−1, ∞)
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
A) Localización y separación de las raíces
V.Álvarez
J.A. Armario
F. Muñoz
Analíticamente:
Crecimiento: signo f ’(x)
Bolzano: f continua en [a,b], f(a)·f(b)<0
-
lim f ( x) = −1 < 0
x → −∞
↓
-1
↑
1
f (−1) − − 1 < 0
e
+
lim f ( x) = +∞ > 0
x →∞
Por tanto:
• f (−∞) ⋅ f (−1) > 0
• f (−1) ⋅ f (+∞) < 0
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
A) Localización y separación de las raíces
Analíticamente:
Crecimiento: signo f ’(x)
Bolzano: f continua en [a,b], f(a)·f(b)<0
1.- La función f(x) es continua en (-∞, ∞), f ↓ (− ∞,−1) f ↑ (− 1,+∞ )
2.- f (0) = −1 < 0
3.- f (1) = e − 1 > 0
Conclusión: existe un cero de f(x) en (0,1)
V.Álvarez
J.A. Armario
F. Muñoz
Además, es único, pues f es continua y monótona en (0,1)
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
A) Localización y separación de las raíces: funciones polinómicas
V.Álvarez
J.A. Armario
F. Muñoz
Ejemplo: Los ceros de la función
g 0 ( x) = 2 x 4 − 4 x3 − x 2 + 3 x + 1.
cumplen que:
por tanto:
1
1
4
=
<| x |< 1 + = 3
5 1+ 4
2
1
1 1 

x ∈  − 3,−  ∪  ,3 
5 5 

Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
A) Localización y separación de las raíces: funciones polinómicas
V.Álvarez
J.A. Armario
F. Muñoz
Regla de Laguerre:
Dado un número real positivo, c, tal que
P( x) = ( x − c) (b 0 x n −1 + L + b n -2 x + b n -1 ) + r
r , b 0 , L, b n -2 , b n -1 ≥ 0 o bien r , b 0 ,L , b n -2 , b n -1 ≤ 0
Entonces c es una cota superior para las raíces positivas.
Además:
n 1
P
(
x
)
=
x
R  , c=cota superior de las raíces positivas de R(x)
• Si
 x
entonces, 1/c = cota inferior de las raíces positivas de P(x)
• Si c=cota superior (inferior) de las raíces positivas de P(-x), entonces
-c = cota inferior (superior) de las raíces negativas de P(x).
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
A) Localización y separación de las raíces: Método de Sturm
V.Álvarez
J.A. Armario
F. Muñoz
Definición
Una sucesión de Sturm para una función f(x) en [a,b] es un
conjunto f0(x)=f(x), f1(x), f2(x),…,fn(x) de funciones continuas en
dicho intervalo que satisfacen:
•
fn ( x) ≠ 0 cualquiera que sea x∈[a,b]
•
fi (c) = 0 ⇒ fi −1 (c) ⋅ fi +1 (c) < 0
•
f0 (c ) = 0 ⇒
f0 ( x)
f1 ( x )
Pasa de negativa a
positiva en c.
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
A) Localización y separación de las raíces: Método de Sturm
Teorema de Sturm
Sea f0(x), f1(x), f2(x),…,fn(x) una sucesión de Sturm para f(x)=f0(x)
en [a,b] y consideremos las sucesiones siguientes:
1.
sig[f0(a)], sig[f1(a)],…, sig[fn(a)]
2.
sig[f0(b)], sig[f1 (b)],…, sig[fn(b)]
en las que sig(d) denota el signo de d (indistintamente +/- cuando
d=0).
Sea +1= número de cambios de signo en la sucesión 1.
Sea +2= número de cambios de signo en la sucesión 2.
Entonces, el número de raíces existentes en intervalo [a,b] de la
V.Álvarez
J.A. Armario
F. Muñoz
ecuación f(x)=0 viene dado por +1-+2.
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
A) Localización y separación de las raíces: Método de Sturm
V.Álvarez
J.A. Armario
F. Muñoz
Método para generar una sucesión de Sturm para
P ( x) = a0 x n + a1 x n −1 + L + an −1 x + a0 o un polinomio equivalente.
Pasos:
f0(x)=P(x)
f1(x)=P´(x),
,
f2(x)=-r1(x) donde
r1(x) denota el resto de dividir f0(x) entre f1(x).
En general:
fi+1(x)=-ri(x) donde ri(x) denota el resto de dividir fi-1(x) entre fi(x).
¿Cuándo se termina?
• Si rk(x)=l≠0, entonces {fk(x)}0≤i≤k+1 es una sucesión de Sturm para P(x).
• Si rk(x)=0, entonces P(x) tiene ceros múltiples y fk(x)=m.c.d(P,P´)
Q( x) =
P( x)
f k ( x)
 fi ( x) 


 f k ( x ) 0 ≤ i ≤ k
es equivalente a P(x) con todos su ceros simples.
es una sucesión de Sturm para Q(x).
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
Pasos a seguir para resolver f(x)=0
V.Álvarez
J.A. Armario
F. Muñoz
A) Localización y separación de las raíces: Método de Sturm
Ejemplo: Localizar y separar los ceros de
P( x) = 2 x 6 − 6 x 5 + x 4 + 8 x 3 − x 2 − 4 x − 1
Paso 1:
f 0 ( x) = 2 x 6 − 6 x5 + x 4 + 8 x3 − x 2 − 4 x − 1
Paso 2:
f 0 ´( x) = 12 x5 − 30 x 4 + 4 x3 + 24 x 2 − 2 x − 4
f1 ( x) = 6 x 5 − 15 x 4 + 2 x 3 + 12 x 2 − x − 2
Siempre podemos
multiplicar o dividir por
un número positivo
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
Pasos a seguir para resolver f(x)=0
V.Álvarez
J.A. Armario
F. Muñoz
A) Localización y separación de las raíces: Método de Sturm
Ejemplo: Localizar y separar los ceros de
P( x) = 2 x 6 − 6 x 5 + x 4 + 8 x 3 − x 2 − 4 x − 1
= 13 x 4 − 26 x3 − 8 x 2 + 21x + 8
Paso 3: Cálculo de f2(x)
2 x6 − 6 x5 + x 4 + 8x3 − x 2 − 4 x − 1
6 x 5 − 15 x 4 + 2 x 3 + 12 x 2 − x − 2
x −1
Multiplicamos por 3
6 x 6 − 18 x5 + 3 x 4 + 24 x3 − 3x 2 − 12 x − 3
−6 x 6 + 15 x5 − 2 x 4 − 12 x 3 + x 2 + 2 x
−3 x + x + 12 x − 2 x − 10 x − 3
5
4
3
2
Multiplicamos por 2
−6 x5 + 2 x 4 + 24 x3 − 4 x 2 − 20 x − 6
6 x 5 − 15 x 4 + 2 x3 + 12 x 2 − x − 2
−13 x 4 + 26 x3 + 8 x 2 − 21x − 8
Siempre podemos
multiplicar o dividir por
un número positivo
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
Pasos a seguir para resolver f(x)=0
V.Álvarez
J.A. Armario
F. Muñoz
A) Localización y separación de las raíces: Método de Sturm
Ejemplo: Localizar y separar los ceros de
P( x) = 2 x 6 − 6 x 5 + x 4 + 8 x 3 − x 2 − 4 x − 1
Paso 4: Cálculo de f3(x)
= 2 x3 − 3x 2 − x + 1
6 x 5 − 15 x 4 + 2 x 3 + 12 x 2 − x − 2
Multiplicamos por 13
78 x5 − 195 x 4 + 26 x3 + 156 x 2 − 13 x − 26
−78 x5 + 156 x 4 + 48 x3 − 126 x 2 − 48 x
−39 x 4 + 74 x3 + 30 x 2 − 61x − 26
39 x 4 − 78 x 3 − 24 x 2 + 63 x + 24
−4 x3 + 6 x 2 + 2 x − 2
13x 4 − 26 x 3 − 8 x 2 + 21x + 8
6x −3
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
Pasos a seguir para resolver f(x)=0
V.Álvarez
J.A. Armario
F. Muñoz
A) Localización y separación de las raíces: Método de Sturm
Ejemplo: Localizar y separar los ceros de
P( x) = 2 x 6 − 6 x 5 + x 4 + 8 x 3 − x 2 − 4 x − 1
Paso 5: Cálculo de f4(x) = x 2 − x − 1
13x 4 − 26 x 3 − 8 x 2 + 21x + 8
Multiplicamos por 2
26 x 4 − 52 x3 − 16 x 2 + 42 x + 16
−26 x 4 + 39 x3 + 13 x 2 − 13x
−13 x3 − 3 x 2 + 29 x + 16
Multiplicamos por 2
−26 x3 − 6 x 2 + 58 x + 32
26 x 3 − 39 x 2 − 13 x + 13
−45 x 2 + 45 x + 45
2 x3 − 3x 2 − x + 1
13x−13
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
Pasos a seguir para resolver f(x)=0
V.Álvarez
J.A. Armario
F. Muñoz
A) Localización y separación de las raíces: Método de Sturm
Ejemplo: Localizar y separar los ceros de
P( x) = 2 x 6 − 6 x 5 + x 4 + 8 x 3 − x 2 − 4 x − 1
Paso 6: Cálculo de f5(x)
2 x3 − 3x 2 − x + 1
−2 x3 + 2 x 2 + 2 x
−x + x +1
2
+ x2 − x −1
0
PARAR r4(x)=0
x2 − x −1
2x −1
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
Pasos a seguir para resolver f(x)=0
V.Álvarez
J.A. Armario
F. Muñoz
A) Localización y separación de las raíces: Método de Sturm
Ejemplo: Localizar y separar los ceros de
P( x) = 2 x 6 − 6 x 5 + x 4 + 8 x 3 − x 2 − 4 x − 1
Al ser el r4(x)=0, se tiene:
• P(x) tiene ceros múltiples.
• m.c.d ( P, P ') = f 4 ( x) = x − x − 1.
2
En consecuencia Q( x) =
P( x)
f 4 ( x)
tiene los mismo ceros que P(x)
pero todos simples.
Además, una sucesión de Sturm para Q(x) es: g 0 ( x) = Q( x),
f1 ( x)
f 2 ( x)
f 4 ( x)
g1 ( x) =
, g 2 ( x) =
, g3 ( x) =
,
f 4 ( x)
f 4 ( x)
f 4 ( x)
f 4 ( x)
g 4 ( x) =
.
f 4 ( x)
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
Pasos a seguir para resolver f(x)=0
V.Álvarez
J.A. Armario
F. Muñoz
A) Localización y separación de las raíces: Método de Sturm
Ejemplo: Localizar y separar los ceros de
P( x) = 2 x 6 − 6 x 5 + x 4 + 8 x 3 − x 2 − 4 x − 1
Sucesión de Sturm:
g 0 ( x) = 2 x 4 − 4 x3 − x 2 + 3 x + 1.
g1 ( x) = 6 x 3 − 9 x 2 − x + 2.
g 2 ( x) = 13x − 13 x − 8.
2
g3 ( x) = 2 x − 1.
g 4 ( x) = 1.
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
Pasos a seguir para resolver f(x)=0
V.Álvarez
J.A. Armario
F. Muñoz
A) Localización y separación de las raíces: Método de Sturm
Ejemplo: Localizar y separar los ceros de
P( x) = 2 x 6 − 6 x 5 + x 4 + 8 x 3 − x 2 − 4 x − 1
− ∞ − 3,−2,−1 − 0.5
0
1 1.5 2, 3 ∞
+
+
−
−
+
+
−
−
+
+
g4(x)=1
+
−
+
−
+
+
−
+
−
+
−
−
+
−
+
Cambios de
signo
4
4
3 2
g0(x)
g1(x)
g2(x)
g3(x)
1 cero
2 ceros
−
+
+
+
+
+
+
+
+
+
+
+
+
+
+
2 1 0 0
ceros 1 cero
14 cero
2 ceros1 cero
g 0 ( x) = 2 x 4 − 4 x 3 − x 2 + 3 x + 1.
g1 ( x) = 6 x 3 − 9 x 2 − x + 2.
g 2 ( x) = 13x 2 − 13 x − 8.
g3 ( x) = 2 x − 1.
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
A) Localización y separación de las raíces
V.Álvarez
J.A. Armario
F. Muñoz
Método gráfico: a modo de orientación
Analíticamente:
Crecimiento: signo f ’(x)
Bolzano: f continua en [a,b], f(a)·f(b)<0
Sucesiones de Sturm: caso de polinomios
B) Aproximación numérica de cada una de las raíces
Bisección: si se satisface Bolzano
ewton: si se satisface Fourier
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de la bisección
V.Álvarez
J.A. Armario
F. Muñoz
Bisección: si f(x) continua en [a,b], f(a)·f(b)<0
y f’(x) no cambia de signo en [a,b].
Entonces:
Paso 0:
f(x)= xex-1 continua y creciente en [0,1]
f(0)=-1<0, f(1)=e-1>0.
I0=[a0,, b0] donde a0=0 y b0=1
x0=0.5
1
f(1)>0
0
f(0)<0
ε0=0.5
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de la bisección
V.Álvarez
J.A. Armario
F. Muñoz
Paso 1:
I1=[a1,, b1] donde a1=0.5 y b1=1
La raíz se encuentra aquí
x0=0.5
0
f(0)<0
x1=0.75
1
f(0.5)<0
ε1
f(1)>0
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de la bisección
V.Álvarez
J.A. Armario
F. Muñoz
Conclusión: si f(x) continua en [a,b], f(a)·f(b)<0
y f’(x) no cambia de signo en [a,b].
•El método de bisección nos genera una sucesión en [a,b]:
x0 , x1 , x2 ,…, xn ,…
que converge a la raíz de la ecuación.
Una cota del error es:
Entonces:
b−a
ε n =| x − xn |≤ n +1
2
1
ε n +1 = ε n
2
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
A) Localización y separación de las raíces
V.Álvarez
J.A. Armario
F. Muñoz
Método gráfico: a modo de orientación
Analíticamente:
Crecimiento: signo f ’(x)
Bolzano: f continua en [a,b], f(a)·f(b)<0
Sucesiones de Sturm: caso de polinomios
B) Aproximación numérica de cada una de las raíces
Bisección: si se satisface Bolzano
ewton: si se satisface Fourier
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Interpretación geométrica:
Gráfica de f(x)=xex-1 en [0,1]
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Interpretación geométrica:
Gráfica de f(x)=xex-1 en [0,1]
x1=x0-f(x0)/f’(x0)
x0
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Interpretación geométrica:
Gráfica de f(x)=xex-1 en [0,1]
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
f ( xn )

 xn +1 = xn −
f '( xn )
Fórmula de Newton-Raphson 
x
 0
Fórmula de N-R para f(x)=xex-1. Comenzando en x0=1.
Primera iteración:
f ( x0 )
f (1)
x1 = x0 −
= 1−
= 0.683940...
f '( x0 )
f '(1)
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Fórmula de N-R para f(x)=xex-1. Comenzando en x0=1.
Segunda iteración:
f ( x1 )
x2 = x1 −
= 0.577455...
f '( x1 )
Tercera iteración:
f ( x2 )
x3 = x2 −
= 0.567228...
f '( x2 )
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Método de ewton
Cuestiones:
•¿La sucesión x0, x1, x2,… converge a la raíz de la ecuación?
Condición suficiente: Regla de Fourier
•¿Podemos dar una cota del error que se comete en cada iteración?
Cota del error
•¿Importa el valor que se dé a x0?
Sí
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Regla de Fourier:
Dada una ecuación f(x)=0, f continua y derivable en [a,b].
Si cumple que:
1.
En [a,b] hay una raíz.
2. f´(x) y f´´(x) no se anula en [a,b].
Entonces:
La sucesión
Si se toma x0 según la regla:
x0, x1,…,xn,…
a si f (a) ⋅ f ''(a) > 0
x0 = 
b si f (b) ⋅ f ''(b) > 0
generada por el método
de Newton converge a
la única raíz de f(x)=0
en [a,b]. Además
xn ∈ [a, b] para todo n.
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Regla de Fourier:
¿Se satisface la Regla de Fourier para xex-1=0 en [0,1]?
1. Hay una raíz en [0,1].
2. f´(x)=(x+1)ex y f´´(x)=(x+2)ex no se anulan en [0,1].
Como f(1)* f´´(1)>0, si tomamos x0=1 se tiene que la sucesión
x0,x1,…,xn,…
generada por la fórmula de Newton converge a la raíz de la
ecuación que se encuentra en [0,1].
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Cota del error:
Sea x una raíz de la ecuación f(x)=0. Si se cumple que:
x y xn ∈ [a, b]
A partir del Teorema del Valor Medio, obtenemos que:
A partir del desarrollo de Taylor de grado 2, obtenemos que:
ε n +1 ≤ C ⋅ ε n2
( convergencia cuadrática)
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
Cota del error:
Análisis del error por iteración:
f '( x) = ( x + 1)e x
ε n = x − xn ≤
f ( xn )
min x∈[0,1] f '( x)
¿min x∈[0,1] f '( x) ?
 f '( x ) = ( x + 1)e x > 0
x ∈ [0,1] ⇒ 
x
 f ''( x) = ( x + 2)e > 0
Al cumplirse la regla de Fourier:
V.Álvarez
J.A. Armario
F. Muñoz
min x∈[ 0,1] | f ' ( x) |= min{ f ' (0), f ' (1)} = f ' (0) = 1
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Cota del error:
Análisis del error por iteración:
ε n = x − xn ≤
f ( xn )
min x∈[0,1] f '( x)
= f ( xn )
x1 = 0.683940...
ε1 = 0.35534...
x2 = 0.577455...
ε 2 = 0.02874...
x3 = 0.567228...
ε 3 = 0.00023...<10-3
Si tomamos 0.567 como valor aproximado de la raíz , tenemos que
ε = x − 0.567 ≤
f (0.567)
min x∈[0,1] f '( x)
= f (0.567) = 0.000395...<10-3
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Para determinados valores de x0, puede ocurrir que la fórmula
de Newton-Raphson, xn +1 = xn −
f ( xn )
, comenzando en x0 genere
f '( xn )
una sucesión x0,x1,…,xn,…
¿Converge a la raíz la sucesión x0,x1,…,xn,…?
Depende de cada caso.
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación xe
− x2
= 0 tiene a 0 como única raíz.
Veamos qué sucede si intentamos hallar su raíz tomando x0=0.5.
f ( x0 )
f (0.5)
= 0.5 −
= −0.5,
x1 = x0 −
f '( x0 )
f '(0.5)
f ( x1 )
= 0.5
x2 = x1 −
f '( x1 )
Es claro que la sucesión no va a converger.
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación xe
− x2
= 0 tiene a 0 como única raíz.
Veamos qué sucede si intentamos hallar su raíz tomando x0=0.5.
Gráficamente:
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación xe
− x2
= 0 tiene a 0 como única raíz.
Veamos qué sucede si intentamos hallar su raíz tomando x0=0.5.
Gráficamente:
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación xe
− x2
= 0 tiene a 0 como única raíz.
Veamos qué sucede si intentamos hallar su raíz tomando x0=0.5.
Gráficamente:
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación xe
− x2
= 0 tiene a 0 como única raíz.
Veamos qué sucede si intentamos hallar su raíz tomando x0=0.6.
1
f ( xn )
f '( xn )
-1.542857143…
2
-1.953102422…
3
-2.247722750…
4
-2.494602756…
5
-2.712546496…
…
…
n
f ( x) = xe
− x2
xn+1 = xn −
V.Álvarez
J.A. Armario
F. Muñoz
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación xe
− x2
= 0 tiene a 0 como única raíz.
Veamos qué sucede si intentamos hallar su raíz tomando x0=0.6.
Gráficamente:
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación xe
− x2
= 0 tiene a 0 como única raíz.
Veamos qué sucede si intentamos hallar su raíz tomando x0=0.6.
Gráficamente:
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación xe
− x2
= 0 tiene a 0 como única raíz.
Veamos qué sucede si intentamos hallar su raíz tomando x0=0.6.
Gráficamente:
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación xe
− x2
= 0 tiene a 0 como única raíz.
Veamos qué sucede si intentamos hallar su raíz tomando x0=0.6.
Gráficamente:
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación xe
− x2
= 0 tiene a 0 como única raíz.
Veamos qué sucede si intentamos hallar su raíz tomando x0=0.4.
n
xn +1 = xn −
f ( xn )
f '( xn )
1
-0.1882352940…
2
0.0143566916…
3
-0.0000592069…
4
10-15
5
0
…
…
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación xe
− x2
= 0 tiene a 0 como única raíz.
Veamos qué sucede si intentamos hallar su raíz tomando x0=0.4.
Gráficamente:
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación xe
− x2
= 0 tiene a 0 como única raíz.
Veamos qué sucede si intentamos hallar su raíz tomando x0=0.4.
Gráficamente:
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación xe
− x2
= 0 tiene a 0 como única raíz.
Veamos qué sucede si intentamos hallar su raíz tomando x0=0.4.
Gráficamente:
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación xe
− x2
= 0 tiene a 0 como única raíz.
Veamos qué sucede si intentamos hallar su raíz tomando x0=0.4.
Gráficamente:
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
es multiple, por tanto, no cumple las hipótesis de Fourier en [a,b].
Ejemplo: La ecuación x-sen x = 0 posee una única raíz real triple, x = 0.
¿Cómo podremos detectar que se trata de una raíz triple,
al intentar aproximarla por el método de Newton?
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Ejemplo: La ecuación x-sen x = 0 posee una única raíz real triple, x = 0.
Veamos qué sucede si intentamos hallar la raíz de x - sen x = 0
por el método de Newton tomando como x0=1.
n
f ( xn )
xn +1 = xn −
f '( xn )
1
0.310290…
M
M
10
0.016822…
M
M
20
0.000019…
M
M
!!Extremadamente lenta la convergencia!!
Raíz de multiplicidad 3
f(xn) tiende a 0
f’(xn) tiende a 0
f’’(xn) tiende a 0
f’’’(xn) no tiende a 0
f '( x10 ) = 0.0001... f '( x20 ) = 0.00000001...
f ''( x10 ) = 0 '016...
f ''( x20 ) = 0 '0019...
f '''( x10 ) = 0 '9998... f '''( x20 ) = 0 '9999...
Pasos a seguir para resolver f(x)=0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
B) Aproximación numérica de cada raíz: método de Newton
V.Álvarez
J.A. Armario
F. Muñoz
Sea f(x)=0 una ecuación que posee una única raíz en [a,b] y que
es múltiple, con multiplicidad k.
Supongamos que la fórmula de Newton-Raphson comenzando
en un cierto valor de x0 (conocido) converge a la raíz.
f ( xn )

 xn +1 = xn −
f '( xn )

x
 0
¿Cómo acelerar la convergencia de la fórmula de Newton
para hallar la raíz múltiple de f(x)=0 en [a,b]?
f ( xn )

 xn +1 = xn − k
f '( xn )

x
 0
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
Pasos a seguir para resolver f(x)=0
V.Álvarez
J.A. Armario
F. Muñoz
B) Aproximación numérica de cada raíz: método de Newton mejorado
Ejemplo: La ecuación x-sen x = 0 posee una única raíz real triple, x = 0.
Veamos qué sucede si intentamos hallar la raíz de x-sen x=0
por el método de Newton mejorado tomando como x0=1.
n
xn +1 = xn − 3
f ( xn )
f '( xn )
1
-0.034…
2
0.0000013…
3
0.00000000000009…
Podemos observar que en la tercera iteración obtenemos una aproximación
de la raíz mucho mejor que la que obteníamos antes con 20 iteraciones.
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
Pasos a seguir para resolver f(x)=0
V.Álvarez
J.A. Armario
F. Muñoz
B) Aproximación numérica de cada raíz: método de Newton mejorado
Ejemplo: La ecuación x-sen x = 0 posee una única raíz real triple, x = 0.
Veamos qué sucede si intentamos hallar la raíz de x-sen x=0
por el método de Newton mejorado tomando como x0=1.
Gráficamente:
Método Newton
Método Newton mejorado
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
Pasos a seguir para resolver f(x)=0
V.Álvarez
J.A. Armario
F. Muñoz
B) Aproximación numérica de cada raíz: método de Newton mejorado
Ejemplo: La ecuación x-sen x = 0 posee una única raíz real triple, x = 0.
Veamos qué sucede si intentamos hallar la raíz de x-sen x=0
por el método de Newton mejorado tomando como x0=1.
Gráficamente:
Método Newton
Método Newton mejorado
Tema 1: Resolución de ecuaciones no lineales
Cálculo umérico
Pasos a seguir para resolver f(x)=0
V.Álvarez
J.A. Armario
F. Muñoz
B) Aproximación numérica de cada raíz: método de Newton mejorado
Ejemplo: La ecuación x-sen x = 0 posee una única raíz real triple, x = 0.
Veamos qué sucede si intentamos hallar la raíz de x-sen x=0
por el método de Newton mejorado tomando como x0=1.
Gráficamente:
Método Newton
Método Newton mejorado