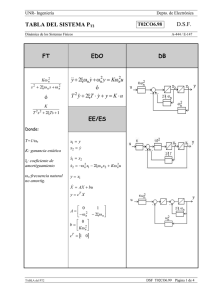
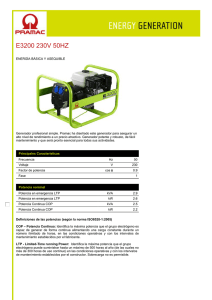
D.S.F. TABLA DEL SISTEMA PT2 FT EDO DB 2 y y y K u ξω ω ω + +
Anuncio

UNR- Ingeniería Depto. de Electrónica TABLA DEL SISTEMA PT2 T02CO5.98 Dinámica de los Sistemas Físicos A-444 / E-147 FT Kω n2 s 2 + 2ξω n s + ω n2 ó D.S.F. EDO DB && y + 2ξωn y& + ωn2 y = Kωn2 u ó 2 T &&y + 2ξT y& + y = K ⋅ u K T s + 2ξTs + 1 2 2 EE/ES Donde : T = 1/ωn K: ganancia estática ξ: coeficiente de amortiguamiento ωn: frecuencia natural no amortiguada x1 = y x2 = y& x&1 = x2 x&2 = −ω n2 x1 − 2ξω n x2 + Kω n2u y = x1 X& = AX + bu y = cT X 1 0 A= 2 − ω n − 2ξω n 0 b= 2 Kω n cT = [1 0] TABLA_PT2.doc DSF T02CO5.98 Página 1 de 4 Respuesta al escalón del PT2 para diferentes parámetros de la FT Polos Amortiguación Respuesta al Escalón h(t) ξ= 0 no amortig. (inestable o marginalmente estable) 0 < ξ <1 subamortig. h(t ) = K − (1) (2) (3) (4) (5) (6) (7) ξ=0 0 < ξ <1 ξ=1 ξ>1 -1 < ξ < 0 ξ = -1 ξ < -1 K 1−ξ 2 e−ξωnt sen(ωa ⋅ t + β ) ξ =1 amortig. crítico h(t ) = K (1 − e−ξωnt − ξωn t e−ξωnt ) ξ >1 ξ = 1 →s1,2 = −ωn ξ >1 →s1,2 = −ξωn ± ωn ξ 2 −1 1 = T1,2 0 < ξ < 1 →s1,2 = −ξωn ± jωn 1 − ξ sobreamort. o aperiódico t t − K − T1 h(t ) = K − T1e − T2e T2 T1 − T2 2 = −σ ± jω a Ubicación en el plano complejo de los polos para 0<ξ<1 TABLA_PT2.doc ξ< 0 inestable DSF T02CO5.98 Página 2 de 4 Características de la respuesta al escalón (0 < ξ < 1): −π ⋅ξ SV = A ⋅ K ⋅ e 1−ξ 2 (Sobrevalor) A: amplitud del escalón de entrada K: ganancia estática − π ⋅ξ D % = 100 ⋅ e 1− ξ 2 tp = π / ωa (Tiempo de Pico o Peak-time) tr ≈ 4/ σ (criterio 2%) tr ≈ 3 / σ (criterio 5%) (Tiempo de Respuesta o Settling-time) tc 0-100% = (π - β) / ωa tc 10-90% ≈ 2.5/ ωa (Tiempo de Crecimiento o Rise-time) TABLA_PT2.doc DSF T02CO5.98 Página 3 de 4 Respuesta frecuencial del PT2 u ( t ) = A s e n (ω ⋅ t ) ⇒ y ( t ) = A ⋅ G ( s = j ω ) ⋅ s e n ω t + R G ( j ω ) = y ⋅ s e n ( ω ⋅ t + Φ ) K G ( jω ) = − | y |d B ω ω + j 2ξ +1 2 ωn ωn 2 = 2 0 log( A K ) − 2 0 log 2ξ Φ = − arctg 1 − TABLA_PT2.doc ω ωn ω2 ω n2 2 2 ω2 ω 1 − 2 + 2ξ ωn ωn DSF T02CO5.98 Página 4 de 4