Document

Temas
Transformada de Laplace:
Tema de la semana
Transformada de Laplace de las funciones
de Heaviside (escalón unitario) y delta
de Dirac (impulso). Propiedad: Segundo Teorema
de traslación. Función impulso y prop. de filtrado.
Transf. Función impulso.
Transformada de Laplace
F ( s ) = L { f ( t )} ≜
L
+∞
∫
• Derivada de funciones generalizadas.
• Segundo Teorema de traslación. Función.
Transformada de un producto.
Convolución.
Transformada de Laplace
e − st f ( t ) dt
0
f (t )
donde:
f (t ) es una función en el tiempo causal.
L {i} es el operador transformada deLaplace
e − st Núcleo de la transformación
t ∈ [ 0, ∞) ⊂ ℝ
L {i}
F (s)
s∈ℂ
s = σ + jω
Transforma una función de dominio de tiempo en
un función de dominio de frecuencia complejo.
s es una variable compleja
F ( s ) es la transform ada de Laplace de f (t )
Es una transformación perteneciente a la familia
de las transformaciones integrales.
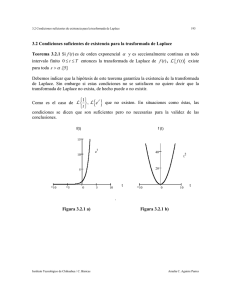
Existencia de la Transformada de Laplace
f (t) causal, continua por tramos en 0, ∞) , de orden exponencial,
Funciones continuas por tramos
f(t)
con abcisa de convergencia σc , entonces:
t
existe la Transformada de Laplace de f (t)
Transformada de Laplace F(s) sólo por definición?
F ( s ) = L { f ( t )} =
+∞
∫
e − st f ( t ) dt , R e( s ) > σ c
0
F ( s ) = L { f (t )} ≜
+∞
∫
e − st f (t ) dt
0
Función escalón unitario de Heavise o
Función escalón unitario
1
H (t ) = 
0
1
H (t − a ) = 
0
(t ≥ 0)
(t < 0)
(t ≥ a)
(t < a )
Ejemplos:
Exprese la función pulso en términos de
funciones escalones unitarios
 K ( a ≤ t < b)
f (t ) = 
0 en otro caso
Expresar la función causal en términos de
funciones escalones unitarios.
t 2

f (t ) = t + 1
2

(0 ≤ t < 1)
(1 ≤ t < 3)
(3 ≤ t )
Transformada de Laplace función escalón
unitario
H (t − a )
K
a
t
a
H (t − a ), a ≥ 0
F ( s ) = L { H (t − a )} =
Transformada de Laplace función pulso
+∞
∫e
− st
+∞
H (t − a )dt =
0
F ( s ) = L { H (t − a)} =
∫e
f (t ) = k ( H (t − a) − H (t − b))
− st
dt
a
e
t
b
− as
F ( s ) = L { f (t )} = k L { H (t − a)} − k L { H (t − b)}
s
Segundo teorema de traslación
Teorema de Heavise o de retraso.
Si L { f (t )} = F ( s ), entonces para una constante positiva a,
L { f (t − a ) H (t − a )} = e − as F ( s )
Transformada de Laplace de una
función periódica
Sea f (t ) una función continua por tramos en 0, ∞ ) ,
de orden exponencial, periódica de período T .
Entonces:
T
1
− st
L { f (t )} =
e
f (t )dt
1 − e −Ts 0
∫
(Demostrar)
Inversión del segundo teorema de traslación
{
}
L −1 e − as F ( s ) = f (t − a ) H (t − a )
Si
L −1{ F ( s )} = f (t ) H (t )
Función impulso unitario o delta de Dirac
Fuerzas impulsivas: el valor está concentrado
en un punto.
si t ≠ a
 δ (t − a ) = 0

δ (t − a ) satisface  +∞
 −∞ δ (t − a)dt = 1
∫
f(t)
δ (t − a )
a
Función impulso
No es una función en sentido usual.
Función generalizada
cálculo
generalizado.
Distribución
teoría de distribuciones.
Función pulso
1

0 (0 < t < a − 2 T )

 A / T (a − 1 T ≤ t < a + 1 T )

φ (t ) = 
2
2

1
(t ≥ a + T )
0
2


∫
+∞
−∞
φ (t )dt = ∫
a +T /2
a −T /2
A
dt
T
t
Transformada de la función impulso
L+ { f (t )} =
L− { f (t )} =
∫
+∞
0+
∫
+∞
0−
Propiedad de filtrado
Si f(t) es continua en t=a , entonces:
e − st f (t ) dt
e
− st
f (t )dt =
∫
0+
0−
L {δ (t )} = L− { f (t )} =
e
∫
− st
+∞
0−
f (t )dt +
∫
+∞
0+
e
− st
f (t )dt
e − st δ (t )dt
Transformada de la función
impulso
L {δ (t − a )} =
∫
+∞
0
− st
e δ (t − a )dt
∫
+∞
−∞
f (t )δ (t − a)dt = f (a)
Permite: aislar o separar el valor en un punto
en particular
Relación entre las funciones escalón e impulso
De las definiciones de las funciones:
H (t ) =
∫
t
−∞
δ (τ )dτ
L {δ (t − a )} = e − as
Inversamente:
{ }
L −1 e − as = δ (t − a )
Demostrarlo !!!
Si t>0
d
H (t ) = H ′(t ) es δ (t )?
dt
Función de prueba
θ (t )
θ (t ) es una función de prueba, entonces
cumple:
Es Continua.
Tiene derivadas continuas de todos los órdenes.
Es igual a cero fuera de un entorno finito.
Para una función generalizada g(t)
Ejemplo:
Función de prueba adoptada por Gabel y
Roberts (Signals and Lineal Systems, Wiley,
New York, 1973) es:
e − d 2 /( d 2 −t 2 )
θ (t ) = 
0
( t < d)
Propiedad de equivalencia
• Se cumple
G (θ ) =
G (θ ) =
∫
∞
−∞
∫
∞
−∞
θ (t ) g (t )dt
Si g1 (t ) y g 2 (t ) son dos funciones
generalizadas entonces :
g1 (t ) = g 2 (t )
θ (t )δ (t )dt = θ (0)
sí y solo sí
∫
∞
−∞
∞
θ (t ) g1 (t )dt = ∫ θ (t ) g 2 (t )dt
−∞
Demostrar
δ (t ) =
d
H (t ) = H ′(t )
dt
Demostración
∫
Para esto debo probar que:
∫
∞
−∞
∞
θ (t )δ (t )dt = ∫ θ (t ) H ′(t )dt
−∞
∞
−∞
∞
θ (t ) H ′(t )dt = [θ (t ) H (t )]−∞ − ∫ θ ′(t ) H (t )dt =
∞
−∞
= 0−
∫
∞
0
θ ′(t )dt = − [θ (t )]0 = θ (0)
∞
Además por propiedad de filtrado:
∫
∞
−∞
θ (t )δ (t )dt =θ (0)
(2)
Y luego aplico prop. de equivalencia
De (1)=(2) aplico Propiedad de equivalencia
Derivada de funciones generalizadas:
Calcular la derivada de la función
causal:
Parto de:
( f (t ).g (t ) )′ = f ′(t ) g (t ) + f (t ) g ′(t )
t 2 (0 ≤ t < 1)

t + 1 (1 ≤ t < 3)
f (t ) = 
(t ≥ 3)
2


(1)