INTERVALO DE CONFIANZA PARA LA MEDIA DE LA POBLACIÓN :

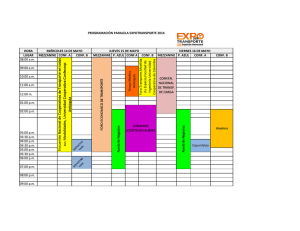
INTERVALO DE CONFIANZA PARA LA MEDIA DE LA POBLACIÓN : 
En la realidad, normalmente no se conoce cómo es una población ( se conoce  , pero
no se conoce  ). Sin embargo, se puede estudiar una muestra de esa población y del
conocimiento de la muestra sacar conclusiones sobre la población.
Si de una población se conoce su desviación típica  y buscamos un intervalo en el que
esté la media  con un nivel de confianza del 1    %, el intervalo es:


 
 X  z 
,
X

z

siempre que la población de partida sea Normal o el


n
n 
2
2

tamaño de la muestra n  30 .
Error máximo admisible:
Error = z  

2
n
Ejemplo: Si conocemos que la desviación típica para la altura de las chicas de 18 años
en Aragón es 10 cm. Supongamos que hemos tomado una muestra de 100 chicas sale
que la altura media de la muestra: X =170.
a) Hallar los intervalos de confianza para la altura media de las chicas de 18
años en Aragón para un nivel de confianza del 90%, 95% y 99% y el error
máximo en cada caso:
Nivel de conf.del 90%: (170
10
1,645 , 170
10
Nivel de conf.del 99%: (170
10
 2,575 , 170
10
1,645) = (168,355 , 171,645)
100
100
10
= 1,645
Error  1,645
100
10
10
Nivel de conf.del 95%: (170
1,96 , 170
1,96) = (168,04, 171,96)
100
100
10
= 1,96
Error  1,96 
100
100
10
= 2,575
Error  2,575
100
 2,575) = (167,425 , 172,575)
100
b) Para un nivel de confianza del 95% ¿ Cuál debe ser el tamaño de la muestra
para que el error máximo admisible sea menor que 1 cm.?
Error  1,96 
10
 1 , despejado n queda: 19,6<
n
decir, el tamaño de la muestra debe ser 385 o más.
n  n  (19,6) 2  n  384,16 es