Vamos a analizar la dinámica de peque˜nas variaciones

ETSECCPB (Eng. Civil, Fı́sica - 205104)
Lección 8: Ondas longitudinales de presión en un tubo de gas
Dept. Fı́sica Aplicada (UPC)
A. Meseguer
Vamos a analizar la dinámica de pequeñas variaciones (fluctuaciones) de presión, densidad y temperatura de un gas en confinado en un tubo cilı́ndrico de sección transversal uniforme de área A.
s(x + ∆x, t)
∆x
∆m
(p0 , V0 , T0 )
∆m
̺0 =
V0
x
∆m
p0 + p
V0 + V
T0 + T
̺0 + ̺
A
x + ∆x
s(x, t)
A
∆x̃
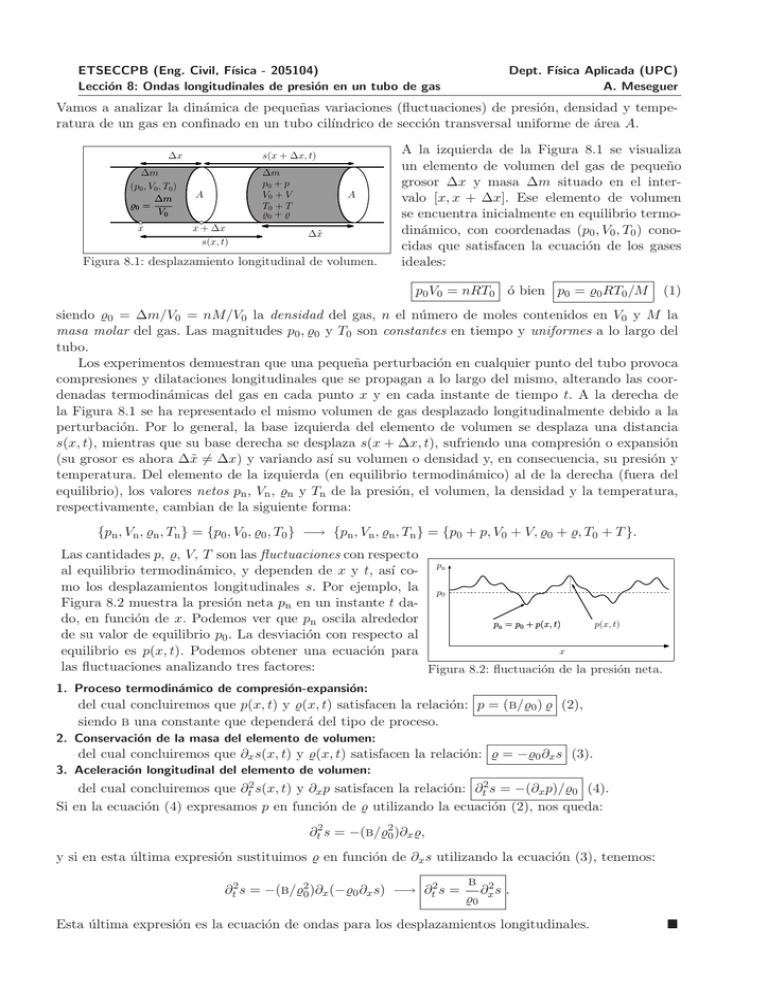
Figura 8.1: desplazamiento longitudinal de volumen.
A la izquierda de la Figura 8.1 se visualiza
un elemento de volumen del gas de pequeño
grosor ∆x y masa ∆m situado en el intervalo [x, x + ∆x]. Ese elemento de volumen
se encuentra inicialmente en equilibrio termodinámico, con coordenadas (p0 , V0 , T0 ) conocidas que satisfacen la ecuación de los gases
ideales:
p0 V0 = nRT0 ó bien p0 = ̺0 RT0 /M
(1)
siendo ̺0 = ∆m/V0 = nM/V0 la densidad del gas, n el número de moles contenidos en V0 y M la
masa molar del gas. Las magnitudes p0 , ̺0 y T0 son constantes en tiempo y uniformes a lo largo del
tubo.
Los experimentos demuestran que una pequeña perturbación en cualquier punto del tubo provoca
compresiones y dilataciones longitudinales que se propagan a lo largo del mismo, alterando las coordenadas termodinámicas del gas en cada punto x y en cada instante de tiempo t. A la derecha de
la Figura 8.1 se ha representado el mismo volumen de gas desplazado longitudinalmente debido a la
perturbación. Por lo general, la base izquierda del elemento de volumen se desplaza una distancia
s(x, t), mientras que su base derecha se desplaza s(x + ∆x, t), sufriendo una compresión o expansión
(su grosor es ahora ∆x̃ 6= ∆x) y variando ası́ su volumen o densidad y, en consecuencia, su presión y
temperatura. Del elemento de la izquierda (en equilibrio termodinámico) al de la derecha (fuera del
equilibrio), los valores netos pn , Vn , ̺n y Tn de la presión, el volumen, la densidad y la temperatura,
respectivamente, cambian de la siguiente forma:
{pn , Vn , ̺n , Tn } = {p0 , V0 , ̺0 , T0 } −→ {pn , Vn , ̺n , Tn } = {p0 + p, V0 + V, ̺0 + ̺, T0 + T }.
Las cantidades p, ̺, V, T son las fluctuaciones con respecto
al equilibrio termodinámico, y dependen de x y t, ası́ co- pn
mo los desplazamientos longitudinales s. Por ejemplo, la p0
Figura 8.2 muestra la presión neta pn en un instante t dado, en función de x. Podemos ver que pn oscila alrededor
pn = p0 + p(x, t)
p(x, t)
de su valor de equilibrio p0 . La desviación con respecto al
x
equilibrio es p(x, t). Podemos obtener una ecuación para
las fluctuaciones analizando tres factores:
Figura 8.2: fluctuación de la presión neta.
1. Proceso termodinámico de compresión-expansión:
del cual concluiremos que p(x, t) y ̺(x, t) satisfacen la relación: p = (b/̺0 ) ̺ (2),
siendo b una constante que dependerá del tipo de proceso.
2. Conservación de la masa del elemento de volumen:
del cual concluiremos que ∂x s(x, t) y ̺(x, t) satisfacen la relación: ̺ = −̺0 ∂x s (3).
3. Aceleración longitudinal del elemento de volumen:
del cual concluiremos que ∂t2 s(x, t) y ∂x p satisfacen la relación: ∂t2 s = −(∂x p)/̺0 (4).
Si en la ecuación (4) expresamos p en función de ̺ utilizando la ecuación (2), nos queda:
∂t2 s = −(b/̺20 )∂x ̺,
y si en esta última expresión sustituimos ̺ en función de ∂x s utilizando la ecuación (3), tenemos:
∂t2 s = −(b/̺20 )∂x (−̺0 ∂x s) −→ ∂t2 s =
b 2
∂ s.
̺0 x
Esta última expresión es la ecuación de ondas para los desplazamientos longitudinales.
Previo (aproximación de Taylor a primer orden):
Consideremos la función f(x) = (1 + x)β , con β
constante. Si x ≈ 0, es decir, si x es una cantidad
pequeña, podemos approximar el valor de esa función por su desarrollo de Taylor a primer orden. En
este caso f(0) = 1 y f ′ (0) = β, con lo cual:
(1 + x)β ≈ 1 + βx (para |x| ≪ 1).
Haremos uso de esta aproximación varias veces en
el desarrollo de nuestra deducción de las ecuaciones
(2), (3) y (4).
Ejemplo (1): tómese β = 1.4 y x = 0.01. En ese
caso: (1 + 0.01)1.4 = 1.014027944. La aproximación de Taylor es: 1+1.4·0.01 = 1.014. Luego, para valores de x del orden de la centésima,
nuestra aproximación tiene un error relativo
menor que un 0.003 %.
Ejemplo (2): tómese β = −1 y x = 0.023.
En este caso: (1 + 0.023)−1 = 0.97751710,
mientras que la aproximación de Taylor es:
1 − 1.0 · 0.023 = 0.977.
1. Proceso termodinámico de compresión-expansión:
Primero supondremos que el proceso es adiabático reversible debido a que los intercambios de calor
son despreciables. Los valores netos iniciales de presión, volumen y temperatura del elemento antes
de ser desplazado y comprimido-expandido eran pn = p0 , Vn = V0 y Tn = T0 . Posteriormente estos
valores netos pasan a ser p0 + p, V0 + V , etc., siguiendo la relación adiabática:
(p0 + p)(V0 + V )γ = p0 V0γ , o bien, en función de la densidad: (p0 + p)(̺0 + ̺)−γ = p0 ̺−γ
0 .
Aislando p0 + p de esta última expresión, nos queda:
̺ γ
γp0
̺
γp0
−γ
γ
p0 + p = p0 ̺0 (̺0 + ̺) = p0 1 +
̺→ p=
̺ .
≈ p0 1 + γ
= p0 +
̺0
̺0
̺0
̺0
Nótese que la aproximación de Taylor que hemos utilizado con β = γ está justificada dado que
|x| = |̺/̺0 | ≪ 1, es decir, las variaciones de densidad ̺ son muy pequeñas frente a la densidad de
equilibrio ̺0 .
Suponiendo que el proceso hubiera sido isotermo (algo que posteriormente descartaremos), el análisis es idéntico, con la única diferencia que la ecuación de la transformación ahora tiene, matemáticamente, un exponente de γ = 1. En cualquiera de los dos casos:
b
p0 γ (adiab.)
p=
̺, con b =
p0
(isot.)
̺0
2. Conservación de la masa del elemento de volumen: La masa de los elementos izquierdo (∆mi ) y
derecho (∆md ) de la Figura 8.1 debe ser la misma, por lo tanto:
∆mi = ̺0 ∆xA = ∆md = (̺0 +̺)∆x′ A = (̺0 +̺)(x+∆x+s(x+∆x, t)−x−s(x, t))A ≈ (̺0 + ̺)∆x(1 + ∂x s)A .
Luego:
̺0
=
(1 + ∂x s) =
̺0 + ̺
̺ −1
̺
1+
−→ ̺ = −̺0 ∂x s
≈1−
̺0
̺0
3. Aceleración longitudinal del elemento de volumen: La aceleración en la dirección x es ax = ∂t2 s(x, t).
La segunda ley de Newton nos relaciona dicha aceleración con el balance de presiones (fuerzas) a
izquierda y derecha del elemento de volumen:
∆max =
X
Fx −→ ̺0 A∆x∂t2 s = A[p(x, t) − p(x + ∆x, t)] ≈ −A∆x∂x p −→ ∂t2 s = −
2
1
∂x p
̺0