Termodinámica, m´odulo teorıa, c´odigo SIA: 2016691 Segundo

Termodinámica, módulo teorı́a, código SIA: 2016691
Segundo semestre de 2010
NOTAS DE CLASE
Profesor: Benjamı́n Calvo-mozo
13 de Agosto de 2010
1. Introducción
1.1 Breve reseña histórica.
1.2 Sistemas, frontera, entorno.
1.3 Variables termodinámicas, equilibrio termodinámico, estado.
1.4 Cambios cuasi-estáticos. Reversibilidad.
1.5 Grados de libertad de un sistema termodinámico.
1.6 Unidades usuales de energı́a (calorı́a, BTU, J).
2. Principio cero
2.1 Enunciado, temperatura empı́rica.
2.2 Escalas Celsius y Fahrenheit.
2.3 Escala de los gases ideales.
2.4 Temperatura termodinámica.
3. Primer principio de la termodinámica
3.1 Trabajo, energı́a interna y calor (“primera ley tradicional”).
3.2 Primer principio.
3.3 Aplicaciones en diversos sistemas.
3.4 Calores especı́ficos.
3.5 Entalpı́a.
3.6 Flujos en procesos.
3.7 Procesos adiabáticos y politrópicos.
3.8 Contracción de Kelvin-Helmholtz.
1
4. Segundo principio
4.1 Función de este principio.
4.2 Procesos cı́clicos y motores térmicos.
4.3 Enunciados clásicos del segundo principio.
4.4 Grado de calor y temperatura.
4.5 Teorema de Carnot.
4.6 Sobre la T termodinámica
4.7 Unicidad de las adiabátas reversibles.
4.8 refrigeradores y bombas térmicas.
4.9 Máquinas térmicas reales.
5. Entropı́a
5.1 Teorema de Clausius (η ≤ ηrev ).
δQ
).
T
≥ δQ
).
T
5.2 Entropı́a (procesos reversibles) (dS =
5.3 Entropı́a (procesos irreversibles) (dS
5.4 Primer principio con entropı́a.
5.5 Entropı́a y degradación de la energı́a.
5.6 Entropı́a y orden
→ S = k log g.
5.7 Calores especı́ficos y sus anomalı́as. (transición orden-desorden; 50-50 Cu-Zn latı́n ∼ 460 C ).
5.8 Calor latente.
6. Formulación de Carathéodory del segundo principio
6.1 Entropı́a empı́rica y calor (σ = σ(xi , Θ)).
6.2 Temperatur termodinámica y entropı́a (δQ ≤ T 0 dS ).
6.3 Transformaciones irreversibles.
7. Potenciales termodinámicos
7.1 Funciones potenciales.
7.2 transformaciones de Legendre.
7.3 Relaciones de Maxwell.
2
8. Aplicación a sistemas sencillos
8.1 Algunas propiedades de los calores especı́ficos.
8.2 Gas perfecto (ideal).
8.3 Comportamiento de sustancias puras reales.
8.4 Filamento elástico.
8.5 Pila eléctrica reversible.
8.6 Tensión superficial (3 grados de libertad) (dU = T dS − PdV + γdA).
8.7 Piezoelectricidad (dU = T dS + F dL + E dP).
8.8 Efecto magnetocalórico.
8.9 Radiación térmica.
9. Aplicaciones a algunas transformaciones reversibles
9.1 Expansión de Joule.
9.2 Expansión de Joule-Kelvin.
9.3 Licuefacción de gases.
9.4 Termoelectricidad.
10. Cambios de Fase
10.1 Sistemas de más de una fuente.
10.2 Condiciones generales del equilibrio termodinámico.
10.3 Condiciones para el equilibrio entre fases.
10.4 La ecuación de Clausius-Clapeyron y su integración.
10.5 Funciones de Gibbs en transmisiones de primer orden.
10.6 Puntos crı́tios.
10.7 Cambios de fase de orden superior; interpretación (segundo orden) y ejes.
10.8 efectos superficiales.
11. Sistemas de varios componentes
11.1 Mezcla de gases ideales.
11.2 Aumento de la entropı́a en la difusión.
11.3 Potencil quı́mico.
11.4 Condiciones para el equilibrio.
11.5 Disoluciones ideales.
11.6 Recciones de gases ideales.
3
12. El tercer principio
12.1 Formulación del tercer principio.
12.2 Consecuencias fı́sicas elementales.
12.3 inaccesibilidad del cero absoluto.
12.4 Transformaciones alotrópicas.
12.5 vidiros.
12.6 Constante de equilibrio.
Calificaciones
Tres parciales cada uno con un valor del 20% sobre la nota final. Problemas 20% y un trabajo final 20%.
4
1
1.1
Introducción
Breve Reseña histórica
De acuerdo con Ingo Muller en el prefacio de su obra “the history of thermodynamics. A dostrine of energy
and entropy, (sic)” el episodio más excitante y significativo de de progreso cientı́fico es el dsarrollo de la electrodinámica y termodinámica en el siglo 19 y comienzos del 20. La naturaleza del calor y la tempratura fue
reconocida, la conversación de la energı́a fue descubierta, y la realización de la equivaalencia entre masa y energı́a suministraron un nuevo combustible, de potencia ilimitada.
Temperatura
El primer concepto termodinámico desarrollado en relación a la sensación de frı́o o calor fue el concepto de
temperatura, que proviene del vocablo latino“temperare”, mezclar, como cuando se mezclan dos lı́quidos. En
sus inicios fueron médicos quienes realizaron los primeros pasos de este concepto. Ası́, Hipócrates (460 - 370
AC) pensó que el desbalance de los fluidos corporales tales como la sangre, flema, bilis negra y amarilla, etc.,
conducen a una enfermedad la cual hace al el cuerpo inusualmente frı́o o caliente, seco o húmedo. Galeno (133 200 AD) otro médico admirador de Hipócrates, tomó la idea y trabajó aún más en este sentido. Asumió que la influencia del lima en la mezcla de los fluidos del cuerpo determinan el caraácter o temperatura de una persona. Ası́,
supuso que el cuerpo y el alma de los habitantes de las tierras frı́as y húmedas del Norte eran silvestres y salvajes
mientras que la gente de las tierras calientes y secas del Sur eran flácidos y sumisos. Luego contuó argumentando
que las personas que vivı́an en zonas bien mezcladas, “temperature”, la gente vivia con propiedades superiores
en cuanto a juicio e intelecto. Galeno mezcló cantidades iguales de agua hirviendo y hielo que el consideraba
como cuerpos a su disposición, más caliente y frı́o respectivamente. Tal mezcla la llamó neutral., y estableció
cuatro grados por encima y cuatro grados por debajo de él. Esta escala de nueve grados se mantuvo en la “edad
oscura de la ciencia” por la tradición de los médicos árabes y re-emergió en Europa durante el Renacimiento. El
primer europeo en usarla, lanzando una hipótesis erronéa, fue Johannis Haslar de Berna, en su obra “De logistica
medica”. Allı́ publicó una tabla en la que la gente muy al Norte (hoy en dı́a esquimales) estaban frı́os en cuatro
grados, mientras que la gente en los trópicos estaban cuatro grados calientes, y por supuesto, la gente que vivı́a
como él estaban con temperatura neutra de cero grados. En su obra se puede ver ese listado de la temperatura
de las personas de acuerdo con su latitud geográfica que él conocı́a, varı́a entre 0 y 90. Hoy en dı́a sabemos
que este raciocinio es falso pues toda pesona sana, independientemente de la latitud donde viva, tiene la misma
temperatura corporal. Obviamente para confrontar dichas hipótesis era necesario construir un termómetro. No
es claro para los historiadores de la ciencia quién lo inventó. Se reporta que en 1592 hizo un primer intento de
termómetro usando la propiedad de expansión/contracción del aire de acuerdo con la temperatura.
Se reporta un termoscópio construido por Galileo en 1620 y un termómetro de alcohol en 1640 por el gran duque
de toscano. Hacia 1700, Jhon Patrick construyó un termómetro con una escala ası́:
90 ◦
85 ◦
75 ◦
65 ◦
extremo frı́o
muy helado
fuertemente helado
helado
55 ◦
45 ◦
35 ◦
25 ◦
aire frı́o
15 ◦
aire templado 5 ◦
aire cálido
0◦
caliente
“sultry”
muy caliente
extremadamente caliente
Una dificultad era establecer cómo dos termómetros marcaran una misma temperatura ante diversas situaciones
5
similares. En las discusiones se propusieron referencias tales como las temeraturas asociadas a (1) el derretimiento de la mantequilla, (2) la temperaqtura de un humano saludable, (3) la temperatura en el techo interior
“cellar” del observatorio de Paris, etc.
Pero los indicadores tales como la fusión del hielo bien sea en agua o en solución salina de agua, y la ebullición
del agua ganaron terreno.
• 1701 Ole Christensen Roner (1644 - 1710) usó un termómetro de vino tinto como indicador. En su escala
7,5 era la temperatura de congelación del agua, 60 la del punto d ebullición del agua y el cero de dicha
escala corresponde a la T de una mezcla de hielo y sal (∼ 25 gK).
• 1714 Daniel Gabriel Fahrenheit (1686 - 1736) inventó el termómetro de mercurio. Inicialmente utilizó una
escala en la que una mezcla de hielo y sal en equilibrio (∼ 255K), 30 el punto de congelación del agua y 90
la temperatura del cuerpo humano. Luego cambió la escala tal que 32 representa el punto de congelación
del agua y 212 como su punto de ebullición.
• 1742 Anders Celsius (1701 - 1744) utilizó una escala en la que el cero representa el punto de ebullición del
agua y 100 el del punto de congelación.
• 1744 Carl Lirmacus (es el padre de la taxonomı́a, 1707 - 1778) sugirió invertir la escala de temperatura de
Celsius de modo tal que o represente la temperatura de fusión del agua y 100 el de ebullición. Esta forma
de la escala centı́grada de Celsius es la usada hoy en dı́a. Sı́mbolo ◦ C.
• 1848 William Thomson (1824 - 1907) propuso una escala termodinámica en la que 0 representa el “cero
absoluto” y utilizó la escala centı́grada como base. Sı́mbolo ◦ K.
• 1859 William Jhon Macquorn Rankine (1820 - 1872) propuso otra escala termodinámica de temperatura
en dond el 0 representa el nuevo cero absoluto y usó los grados de Fahrenheit como base. Sı́mbolo ◦ R.
En 1954 la Décima conferencia general sobre pesos y medidas cambió el nombre de la unidad de la escala de
temperatura termodinámica llamándola Kelvin, denotada K, suprimió la nomenclatura grado Kelvin (◦ K). Allı́
también se redefinió la escala de temperatura Celsius mediante ◦ C = t(K) - 273.15 K.
Presión
Evangelista Torricelli (1608 - 1647). Fue iniciamente secretario en los últimos 3 meses de su vida (Galileo
Galilei 15 de Febrero 1564 - 8 de Enero 1642). Encontró que la altura de la columna de mercurio era de 1/14 de
la correspondiente al agua. Blaise Pascal (19 de Junio 1623 - 19 de Agosto de 1662).
Energı́a
En 1620 Francis Bacun sugirió distinguir entre T y la influencia térmica transferida de una sustancia a otra.
“Calor, en su esencia es movimiento y nada más”. La palabra “energı́a”, del griego νργια, que significa fuerza
efectiva, fué un concepto introducido por Thomas Young (1773 - 1829) en 1807. Inició en el concepto de vis viva
del latı́n → “fuerza viviente”. Al parecer existen indicios de que Tales de Mileto intuı́a el concepto de conservación de energı́a. Es interesante anotar que fueon ingenieros quienes pensaron que además de la conservación
del momentum deberı́a utilizarse el principio de Leibnitz para propósitos prácticos. El quı́mico William Hyde
6
Wollestern también se unió a esto.
Thomas Young mostró que la suma de la energı́a cinética más la potencial gravitacional o la cinética más la potencial elástica se conserva. En 1829 Coriolis acuñó el término “energı́a cinética” y William Rankine en 1853
usó el término “energı́a potencial.
Joseph Black en 1770 distinguió claramente entre temperatura y calor. También fundió hielo añadiendo lentamente calor y notó que la temperatura no cambiaba. Introdujo el concepto de “calor latente”. También, mediante
sus experimentos de mezcla de partes iguales de lı́quidos diferentes a T diferentes, cada uno tenı́a una respuesta
diferente. Introdujo la teorı́aq del “calórico:
i) calórico, fluido elástico que permea todo y cuyas partı́culas se repelen fuertemente.
ii) partı́culas de calórico y de materia se atraen.
iii) el calórico se conserva.
vi) el calórico es bien sensible o atente. Por sensible, se entiende que un cambio en calórico está relacionado
con un cambio de temperatura.
v) El calórico tiene peso.
Antonie Laurent Lavoisiour (1743 - 1794) sumó a los elementos el calórico y la luz. El hizo mediciones precisas
con su calorı́metro del calor involucrado en varios cambios quı́micos.
El calentamiento por fricción se tuvo en cuenta posteriormente, postulando que la fricción reducı́a la atracción
entre la materia y el calórico. El peso del calórico se introdujo para explicar el ligero aumento de peso de ciertos
metales al ser calentados (“calcinación → oxidación). La repulsión entre partı́culas de alórico y la atracción
entre estas y la materia se empleó oara explicar la expansión y contracción de los diferentes cuerpos al calentarse/enfriarse respectivamente.
Robert Julius Mayer (1814 - 1878) introdujo la conservación de la energı́a. Consibió que la “fuerza viva” del
movimiento puede convertirse en calor:
1◦ calor = 1 gramo a 365m de altura
(energı́a potencial gravitacional → “fuerza de caı́da”).
James Precott Joule (1818 - 1889). Él conocı́a que al pasar la corriente por un hilo conductor este se calentaba
en modo directamente proporcional al cuadrado de la corriente que fluye en él. Él introdujo el “equivalente
mecánico” del calor en los siguientes términos:
“La cantidad de calor que es capaz de levar la temperatura de una libra de agua en un grado en la escala de
Fahrenheit, es igual y puede ser convertida en trabajo mecánico tal que puede elevar 838 libras en una altura
vertical de un pié.”
J. P. Joule “Temperature changes by expansion and compresion of air ” Phylosophical Magazine Seriees III, 26
p. 369 ff., 1845. Los mejores valores de sus experimentos los reportó en 1850. Expresó su convencimiento
7
de la consservación de la energı́a diciendo “estoy convencido de que las leyes poderosas de la naturaleza son
indestructibles por virtud del creador”. Luego Mayer “ajustó” su valor a 425 m de altura en Parı́s. Modernamente,
1 calorı́a = 4.18 Joules
Esto lo llevó además a sugerir la existencia de una energı́a interna.
Nota: En 1798 el conde Rumford publicó “An experimental enquiry concerning the source of heat which is exited
by friction” en donde encontró que puliendo un cañon repetidamente no resulta en la perdida de su habilidad para
producir calor y por lo tanto no existe perdida de calórico. Por lo tanto el calórico no debe ser una sustancia que
se conserva.
Hacia 1824 se reportan tablas de procesos medidos en calorı́as.
La ley de los gases ideales es la ecuacón de estado del gas ideal (hipotético). Fue formulada por primera vez por
Émile Clayperon en 1834 como una combinacón de las leyes de Boyle y de Charles. También se puede derivar de
la teorı́a cinética de los gases ideales según lo hicieron en forma primera August Kronig (1856) y Rudolf Clausius
(1857)
pV = νRT
(1)
ν representa el número de moles, R ≈ 8.314472 JK−1 mol−1 en el SI. La ley de los gases combinada es
para un gas dado
p1 V1
p2 V2
=
T1
T2
pV
T
: cte
(2)
La ley de Avogadro, o también conocida como hipótesis de Avogadro, (1811) plantea lo siguiente: “volúmenes
iguales de gases ideales, a la misma presión y temperatura, contienen el mismo número de partı́culas constituyentes.”
1 mol → ocupa ∼ 22.414 lt a STP
ecuación de estado de Van der Waals (propuesta por Johannes D. Van der Waals, 1873)
"
P+a
ν 2 # V
ν
V
− b = RT
para el vapor de agua: a ' 0.547 Pa m3 , b ' 3.052 × 10−5 m3 mol−1 .
Nota: La entropı́a no es una variable extensiva. se resuleve si las partı́culas son indistinguibles.
8
(3)
1.2
Sistemas, frontera, entorno
Por sistema termodinámico entendemos un conjunto de materia ponderable, una porsión del universo material
bajo estudio. Un sistema puede ser sencillo o complejo. Los sistemas se denominan sencillos cuando son, vistos desde un punto de vista macroscópico, homegńeos, isotrópicos,no cargados (eléctricamente), quı́micamente
inertes, que no se ve afectado por la influencia de campos eléctricos y/o magnéticos, y en los que los efectos superficiales (en la frontera o parte de la misma) son despreciables. Cuando un sistema ya no es sencillo tiene algún
grado de complejidad; por ejemplo, puede ser considerado como compuesto de un cierto número de subsistemas
sencillos.
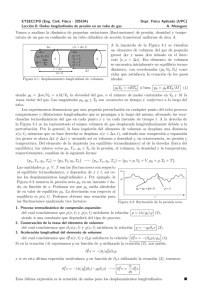
Figure 1: Representación gráfica del sistema, frontera y entorno en el contexto termodinámico.
Todo sistema termodinámico bajo estudio tiene una limitación de extensión espacial en un instante de tiempo
dado. Denominamos la frontera como el conjunto de puntos que delimita el interior del sistema y lo discrimina
de la materia externa a él que denominaremos el entorno. Si a través de la frontera o parte de ella se permite el
intercambio de materia ponderable decimos que el sistema es abierto, en caso contrario decimos que el sistema
es cerrado. Ahora bien, un sistema cerrado puede ser clasificado de tres formas según la interacción o no que
permita su frontera con el entorno. Ası́, tenemos los sistemas aislados, en los que su frontera es tal que no permite
intercambio de energı́a entre este y el entorno, ni la realización de trabjo del uno al otro. En este caso se dice que
la frontera de dicho sistema es una frontera aislante o pared aislante. Si la frontera de un sistema termodinámico
es ahora tal que permite el trabajo entre este y su entorno pero no permite el intercambio de energı́a entre ellos,
se dice que el sistema está aislado térmicamente y su frontera se denomina adiabática. Por último, si se permite
tanto la realización de trabajo en algún sentido entre el sistema y su entorno, están en contacto térmico y a tal
frontera se le califica de diatérmica.
9
1.3
Variables termodinámicas, estado y equilibrio
Como la termodinámica clásica persigue en sus objetivos el estudio de los sistemas térmicos en cuanto a los procesos que involucran intercambio o transformación de energı́a, usando en la descripción propiedades macroscópicas
de dichos sistemas, necesitamos definir entonces variables que representen tales propiedades. A esas variables
se las conoce también como parámetros o coordenadas termodinámicas. No todas las variables termodinámicas
son independientes. Algunos de los parámetros que afectan o pueden afectar un sistema dado corresponden a
propiedades externas, tales como campos eléctricos, magnéticos, etc. externos. Dichos parámetros se denominan
parámetros externos. Otros parámetros son propios del sistema como por ejemplo presión, volumen, temperatura,
etc., y los denominamos “parámetros internos”.
En general, las variables termodinámicas pueden ser clasificadas como “variables intensivas” o “variables extensivas”. si tenemos una variable termodinámica tal que l dividir el sistema en varios subsistemas el valor de
dicha variable permanece igual decimos que la variable es intensiva. Si la variable es extensiva el valor de la
misma en el sistema dado es igual a la suma que toma en los subsistemas. Ejemplos de variables intensivas son
la temperatura, presión, densidad, calor especı́fico. La masa, el volumen, momento magnético, y carga eléctrica
son algunas propiedades extensivas.
En un instante de tiempo dado, definimos “estado” del sistema como una condición reproducible del sistema termodinámico que queda especificada mediante un conjunto de valores d las propiedades macroscópicas medibles
que describen el sistema. de este modo, una propiedad medible del sistema depende del estado del sistema y no
de su historia. Ası́, cuando todos los valores que toman las propiedades que describen un sistema en dos estados
son iguales, tales estados son equivalentes.
Teniendo ya el concepto de estado podemos expresar matemáticamente el concepto de variable termodinámica
intensiva como aquella que puede describirse mediante una función de variables independientes, de grado de
homogeneidad nula. Una función se dice que es homogénea de grado n, si al multiplicar cada una de las variables
independientes por un parámetro real λ, se satisface la relación:
f (λx1 , λx2 ) = λn f (x1 , x2 ).
(4)
Si la función es ahora homogénea de grado uno, describe una variable extensiva. El parámetro λ que afecta a las
variables x1 y x2 se tiene en consideración solo cuando dichas variables son extensivas.
Un concepto fundamental en nuestro desarrollo teórico es el de “equilibrio”. Cuando colocamos dos sistemas en
contacto térmico, usualmente se producen cambios en ambos sistemas hasta que los parámetros que describen
l estado de los sistemas, en particular las variables intensivas, no cambiaran con e tiempo, teniendose entonces
el concepto de equilibrio termodinámico. Si una de las variables intensivas que describen el sistema es el de
la presión, teniéndose además su igualdad en todas partes del sistema tenemos que le mismo goza de equilibrio mecánico. Además, si no acontecen en el sistema reacciones quı́micas y ni estas ni sus reacciones inversas
mantienen la misma tasa de ocurrencia por unidad de tiempo y por unidad de volumen, tenemos una situación de
“equilibrio quı́mico”.
Las configuraciones de equilibrio pueden ser estables, inestables o indiferentes según sea la evolución posterior
a una perturbación que se ejerza sobre el sistema cuando está en un estado de equilibrio. Ası́, si se parte de
una situación de equilibrio y se somete al sitema a una perturbación tal que las variables termodinámicas toman
valores muy cercanos a los que tienen en tal configuración de equilibrio y si la evolución posterior del sistema es:
10
(i) evolucionar hacia los valores que tenı́a cundo estaba en equilibrio, pasa por dichos valores y nuevamente
retorna, y ası́ sucesivamente tratando de evolucionar hacia el estado de equilibrio inicial, se dice que dicho equilibrio es estable.
(ii) evolucionar hacia otro estado de equilibrio con tendencia a permanecer en él, se dice que el estado de equilibrio inicial es indiferente.
(iii) evolucionar hacia otra configuración cualquiera no necesariamente de equilibrio, se tiene que el equilibrio
inicial es inestable.
Se conoce como “termodinámica del euilibrio” aquella parte de la termodinámica clásica que estudia las propiedades
macroscópicas de los sistemas en los estados de equilibrio.
1.4
Cambios cuasiestáticos, reversibilidad
Cuando un sistema cambia de un estado a otro de manera suave, de modo tal que recorre todos los valores
intermedios de sus variables termodinámicas asociadas, se tiene que en un instante de tiempo, estando el sistema
en un estado preliminar bien determinado, un cambio muy fino del mismo se denomina un cambio cuasi-estático.
La figura 2 representa un proceso del estado A al estado B en el que puntualmente se dan cambios cuasi-estáticos
(curva λ) y otro en el que tal condición no se satisface (curva µ).
Figure 2: Representación del cambio de estado termodinámico mediante dos procesos diferentes µ y λ.
11
Un proceso termodinámico es la secuencia evolutiva que describe la evolución de un sistema de un estado a otro.
En la figura 2 λ representa la curva asociada un proceso termodinámico, tales trayectorias representan “caminos
termodinámicos” de los procesos. En ocasiones los procesos mantienen un parámetro termoinámico constante, el
cual puede tener denominación especı́fica. Ası́, si durante el proceso la preión permanece constante, entonces se
habla de un proceso “isobárico”. Un proceso “isocóro” es uno que mantiene constante el volumen del sistema.
Si ahora es la temperatura del sistema la que permanece constante durante el proceso, entonces se habla de un
proceso “isotérmico”. Si durante el proceso no existe intercambio de energı́a térmica a través de la frontera del
sistema se dice que el proceso es “adiabático”. Si la variable termodinámica “entropı́a” es la que permanece
constante a lo largo de todo el proceso, dicho proceso es “isentrópico”. Si la “entalpı́a” es contante en un proceso
se dice “isentálpico”. Algunos caminos termodinámicos toman nombres especı́ficos según el proceso asociado;
en general isoterma, isobara, adiabata, politropa.
Un proceso se dice cı́clico cuando el sistema parte de un estado dado A con ciertos valores de las variables termodinámicas que lo describen, y mediante un proceso suave llega a otro estado B, y si mediante otro proceso, o
varios de ellos, retorna al estado A, se dice que se tiene en composición un “proceso cı́clico”.
Un proceso se denomina “reversible” si mediante un proceso suave inverso y cuasi-estático en cada punto (i.e. en
cada estado intermedio) se puede retornar al estado inicial. De este modo, si en la figura 2 el proceso que ocurre
para llevar al sistema del estado A al estado B mediante un camino termodinámico suave λ, se puede reversar a
lo largo de λ nuevamente al estado A, de manera que no se tenga de forma neta cambio alguno en el sistema ni
en su entorno. Esto en realidad es una idealización ya que para que un sistema sea reversible se necesita que (i) el
camino termodinámico esté descrito mediante una curva suave en un espacio de parámetros termodinámicos del
sistema que ligue dos estados A y B, y que además (ii) entre tales estados no exista histérisis.
Si ahora se lleva el sistema de un estado A (inicial) a otro estado B (final) y no se puede obtener nuevamente el
estado A, entonces se dice que el proceso es irreversible.
Cuando un sistema se encuentra inicialmente en un estado de equilibrio, se le perturba, y si el sistema evoluciona
hacia otro estado de equilibrio (final) se dice que tal proceso de ir de un estado de equilibrio inicial a otro estado
de equilibrio final es un estado de relajación. El intervalo de tiempo transcurrido entre los dos estados luego de la
perturbación inicial se llama “tiempo de relajación”.
1.5
Grados de libertad de un sistema termodinámico
Cuando los estados de u sistema termodinámico se pueden representar con un número mı́nimo de variables
termodinámicas se dice que dicho número representa los “grados de libertad” del sistema térmico dado. Como
regla, uno puede tener cierto número de variables descriptoras del estado del sistema y restarle a dicho número
la cantidad de condiciones que liguen las variables dadas para obtener el número que nos dice cuántos grados
de libertad tiene l sistema. Por ejemplo, para un gas ideal dado como sistema sencillo, tenemos las variables
de estado p,V,T. Pero tenemos la “ecuación de estado” del gas que podemos representar funcionalmente como
p = p(V, T ). Entonces, el gas ideal tiene dos grados de libertad, tres variables menos una condición. Esto implica
que basta tener dos variables temodinámicas independientes para describir sus estados.
1.6
Unidades de energı́a usuales
En la tecnologı́a termodinámica existen varias unidades de enrgı́a pero las más usuales son el Joule (SI), J, el
ergio (CGS), erg, la “calorı́a”, cal, y la unidad térmica británica, BTU.
12
El ergio como unidad de energı́a y trabajo en el sistema CGS se define como la cantidad de trabajo realizado sobre
un sistema desplazándolo 1 cm mediante la aplicación de 1 dina de fuerza externa (sin intercambio de calor). Lo
denotamos erg. 1 erg = 1 dina-cm.
1 dina = 10−7 J ' 6.2415 ×1011 eV.
En SI se define de modo similar (en proceso) a la unidad de trabajo y energı́a, el Joule, denotado J, en honor a
James Prescott Joule1 .
1 J = 1 N m = 107 erg = 1 W s = 1 Pa m3
Calorı́a: 1 cal, introducida por Nicolas Clément en 1821 como una unidad de calor, se define como la cantidad
de energı́a térmica, calor, necesaria para incrementar la temperatura de un gramo de agua en 1 grado entı́grado.
Usualmente se toma en promedio el valor equivalente, 1 cal = 4.184 J. El valor de la calorı́a definida arriba
depende fuertemente de la temperatura inicial del agua manteniendo la temperatura atmosférica en 1 atmosfera.
Ası́, a 4◦ C → 1 cal4 ' 4.204 J, 15◦ C → 1 cal15 ' 4.1855 J, 20◦ C → 1 cal20 ' 4.182 J. Para los nutricionistas
(IUNS → International Union of Nutritional Science) 1 calIUNS = 4.182 J.
A veces se le denomina calorı́a-gramo; existe además la “gran calorı́a” (para 1 kg), también es usual el múltiplo
kilocalorı́a, kcal2 .
1 BTU : british thermal unit.
Se define como la cantidad de calor necesaria para que una libra (1 pound) de agua eleve su temperatura en 1◦ F.
1 libra ' 0.454 kg.
Como
5
T (◦ C) = [T (◦ F) − 32],
9
(5)
5
∆T (◦ C) = [∆T (◦ F).]
9
(6)
entonces
Si ∆T (◦ F) = 1◦ F, entonces ∆T (◦ C) ' 0.5556◦ C.
Valores:
1 W = 1 J s−1 y 1 Pa = 1 N m−2 . El responsable es el Bureau International de Ponds et Mesures. Sistema → SI. El BIPM se creó
en 1875, mayo 20, y hacia 2008 tenı́a ∼51 naciones miembros.
2
standard atmosphere:
1 atm = 101 325 Pa. equivalentemente: 760 mm Hg, 1013.25 mbar, 14.696 PSI.
| {z }
1
Torr
1 bar ≡ 100 kPa = 100 000 Pa ∼ 1 atm |nivel del mar
⇒ 1 mbar = 100 Pa
Ası́ → 1 atm = 1013.25 mbar
13
ISO : 1 BTU ≡ 1055.056 J
USA (15 C : 59◦ F) : 1 BTU ' 1054.804 J
CANADA (15.6◦ C : 60◦ F) : 1 BTU ' 1054.680 J
promedio : 1 BTU ' 1055.870 J
◦
Algunos combustibles liberan una cierta cantidad de energı́a en su combustión3 :
propano →
carbón →
madera seca →
2
∼ 15000BTU/lb
∼ 9000BTU/lb
∼ 7000BTU/lb
Principio cero de la termodinámica
2.1
Temperatura empı́rica
Este principio enuncia una propiedad fundamental de los sistemas en contacto térmico en equilibrio mutuo. En
esencia, el principio establece que si dos sistemas están separadamente en equilibrio térmico con u tercer sistema, entonces los dos primeros sistemas están en equilibrio térmico entre si.
Este principio nos permite afirmar que si un sistema A está en equilibrio con un sistema que sirve de termómetro
y este último maraca cierto valor en la escala preestablecida para el mismo, y si el mismo termómetro indica el
mismo valor en dicha escala de temperaturas cuando entra en contacto térmico y se equilibra con otro sistema B,
entonces los sistemas A y B están en equilibrio térmico. Por ende, si uno de los sistemas citados, digamos A, en
ciertas situaciones, nos establece digamos dos valores de termómetro en situaciones especı́ficas de A, entonces
tal escala del termómetro queda bien establecida para medir temperaturas de diversos sistemas termodinámicos.
Tales situaciones especı́ficas pueden ser por ejemplo la temperatura de fusión del agua de un lado, y la temperatura de ebullición del agua de otro lado, ambas situaciones a una presión de atmósfera estándar. Obviamente se
espera que la dilatación del mercurio, o lı́quido usado como indicador, tenga una respuesta lineal a iguales incrementos de energı́a calórica añadida al sistema de calibración A y luego de ello el termómetro entra en contacto
térmico hasta lograr el equilibrio. Observemos entonces que el principio cero nos permite establecer el concepto
de temperatura empı́rica como se describe en el párrafo anterior.
Formalmente, escojamos tres sistemas, cuyas variables denotaremos con los subindices 1,2,3. Sean además
las variables termodinámicas presión y volumen las que usaremos en la descripción del sistema dado que son
variables bien definidas. Apliquemos el principio cero a las situaciones de equilibrio mencionado en su enunciado.
Digamos que tenemos la condición A consistente con el equilibrio de los sistemas 1 y 3 en contacto térmico.
Esta condición de equilibrio implica que las variables termodinámicas que describen el sistema 1, p1 , V1 , y las
correspondientes l sistema 3, p3 , V3 , están relacionadas al lograr el equilibrio térmico luego de entrar en contacto
mediante una pared diatérmica:
F A (p1 , V1 , p3 , V3 ) = 0.
3
un galón de agua ∼ pounds. Si la calienta de 60 ◦ F → 212◦ F se requieren ∼1200 BTU.
14
(7)
Figure 3: .
Ahora, del equilibrio entre los sistemas 2 y 3, condición B, tenemos:
F B (p2 , V2 , p3 , V3 ) = 0.
(8)
De acuerdo con el principio cero, entonces las situaciones A, B implican una condición C, el equilibrio entre los
sistemas 1 y 2, que podemos esxpresar mediante:
FC (p1 , V1 , p2 , V2 ) = 0.
(9)
De las condiciones A y B podemos despejar p3 :
p3 = fA (p1 , V1 , V3 ),
p3 = fB (p2 , V2 , V3 ).
(10)
De estas dos ecuaciones (10), luego de igualarlas, podemos expresar p1 como función de las variables que quedan:
p1 = g(V1 , p2 , V2 , V3 ).
(11)
De la ecuación (9), condición C, podemos también epresar p1 en función de la otras variables en dicha ecuación:
p1 = fC (V1 , p2 , V2 ).
(12)
De la comparación directa de las ecuaciones (11) y (12) concluı́mos que p1 depende solo de la variables V1 , p2 , V2
y no de V3 ; por lo tanto, V3 se puede eliminar de la ecuación (11), quedando:
15
p1 = g(V1 , p2 , V2 ).
(13)
Pero esta última igualdad provino de igualar las dos ecuaciones (10):
fA (p1 , V1 , V3 ) = fB (p2 , V2 , V3 ).
(14)
Figure 4: .
Entonces V3 tiene una aparación superflua en esta última igualdad. Al hacerlo, obtenemos:
ΦA (p1 , V1 ) = ΦB (p2 , V2 ),
(15)
es decir, esta última igualdad representa lo implicado por el principio cero, que los sistemas 1 y 2 están en
equilibrio térmico ya que separadamente cada uno de ellos lo está con el sistema 3 intermediario. La ecuación
(13) nos lleva a formular la existencia de una función Θ(p, V) cuyos valores (reales) denominamos la temperatura
empı́rica de un sistema. Ası́, re-escribimos la ecuación (13) empleando Θ:
t1 = t2 ,
t1 = Θ(p1 , V1 ),
t2 = Θ(p2 , V2 ).
(16)
Observemos que de acuerdo con la ecuación (16), las ecuaciones (7), (8), (9) pueden entenderse, dado que t1 = t2
según la ecuación (16) significa la condición que estipula que los istemas 1 y 2 están en contacto térmico pero
tal condición, en general, se expresa en unción de las respectivas variables p, V, mediante la ecuación (9). Luego
esta ecuación se puede re-escribir, en virtud de los desarrollado, como:
FC (p1 , V1 , p2 , V2 ) = t1 − t2 = Θ(p1 , V1 ) − Θ(p2 , V2 ) = 0.
Similarmente, las ecuaciones (7) y (8) se pueden re-escribor ası́:
16
(17)
F A (p1 , V1 , p3 , V3 ) = Θ(p1 , V1 ) − Θ(p3 , V3 ) = 0,
F B (p2 , V2 , p3 , V3 ) = Θ(p2 , V2 ) − Θ(p3 , V3 ) = 0.
(18)
En conclusión, dos sistemas en contacto térmico están en equilibrio térmico, si sus temperaturas empı́ricas son
iguales. A cada valor t de la función Θ(p, V) se le llama la temperatura empı́rica del istema y la igualdad t =
Θ(p, V) se le denomina ecuación de estado.
2.2
Escalas de temperaturas: Celsius y Fahrenheit
Las temperaturas empı́ricas inferidas usando el principio cero asociadas con urvas llamadas isotermas, tΘ (p, V),
según expresamos mediante (16) y que graficamos en la figura 4. Estas temperaturas, por tanto, no tienen un nexo
directo con nuestras sensaciones de frı́o o caliente. Para lograr ste nexo, tenemos que recurrir a alguna cantidad
termodinámica x, tal que nos permita establecer una escala lineal de temperatura:
Θ(x) = ax + b
(19)
y de esta manera establecer una escala empı́rica de temperatura. Usualmente utilizamos la expanión lineal de
lı́quidos o gases confinados en una columna cilı́ndrica para establecer graduaciones finas de temperatura. La escala en si se define arbitrariamente, asignando un valor al punto de congelación y otro valor al punto de bullición
del agua. Ası́, en la escala centı́grada tales dos puntos corresponden a los valores de 0◦ C y de 100◦ C. En la escala Fahrenheit a 32◦ F y 212◦ F respectivamente. Los termómetros de gases tubieron amplia favorabilidad hace
tiempo debido a que a presión constante la expanción lineal en volumen de un gas ideal está en correspondencia
lineal con la temperatura. Ahora bien, recordemos la secuencia de los pasos fundamentales de las leyes de los
gases. La primera ley en el escenario histórico es la de Boyle (1662), la cual estipula que a temperatura (empı́rica)
constante, se tiene que p1 V1 = p2 V2 , en donde p1 , V1 son las variables termodinḿicas de presión y volumen del
gas n un cierto estado, y p2 , V2 son los correspondientes valores en otro estado, siempre que la temperatura se
mantenga constante al pasar del estado 1 al estado 2. Pero más de un siglo después Charles (1787) encontró su
ley según la cual, i el cambio de estado ocurre a presión constante, entonces V1 /t1 = V2 /t2 .
Hacia comienzos del siglo XIX, Dalon (1801) descubre su ley de las presiones parciales, la cual estipula que
si tenemos gases separadamente a ciertos valores iguales de temperatura y volumen, teniendo en cada uno de
ellos en u recipiente una presión determinada, entonces, al reunirlos en un cierto lugar con igual volumen y
manteniendo la temperatura, las presiones anteriores se adicionan para dar cuenta de la nueva presión cuando los
gases se mezclan en un solo recipiente. Ası́, si ptexttot es la presión final y p1 , p2 , ..., las presiones de cda gas por
separado, entonces:
ptot = p1 + p2 + p3 + ...
(20)
En 1808 Gay-Lussac estudia el comportamiento de los gases a volumen constante, concluyendo que ante un
cambio de estado se satisface la relación, p1 /t1 = p2 /t2 . Finalmente, Avogadro (1811) lanzó su hipótesis que
establece que gases cuyos estados tengan parámetros iguales en volumen, presión y temperatura, contienen el
mismo número de partı́culas constituyentes del gas. El paso siguiente que sintetiza estas leyes es una ley combinada de los gases y que la estableció Clapeyron mediante:
PV = νR(t + A)
17
(21)
en donde t es la temperatura empı́rica (grados centı́grados para él), A una constante que él asumió A ≈ 265◦ C
y R es ka denominada onstnte de los gases. La presencia de A es necesaria por cuanto al grado cero en alguna
escala de temperatura empı́rica corresponden valores bien definidos y no nulos tanto de presión omo de volumen.
por ejemplo en la escala centı́grada, t : 0◦ C, un mol de gas ideal a una atmósfera de presión ocupa un volumen
aproximado de 22.4 litros (0.0224 m3 ). Es allı́ donde surge la necesidad de buscar una temperatura termodinámica
o temperatura absoluta. El primero en hablar de ello fue Anontons (1702-1703), unas tres décadas después,
Daniel Bernulli propuso en 1734 una teorı́a cinética molecular en la que según él, la presión ejercida por el gas
sobre las paredes del contenedor es la contribución de muchas colisiones realizadas por las moléculas constitutivas
del gas dotadas de movimiento independientes. Siguiendo esta lı́nea de pensamiento, Lambert (1777) habló del
cero absoluto en temperatura termodinámica correspondiente a la situación en la que la presión del gas tiende
a cero. El primero en estimar un valor de temperatura empı́rica del cero absoluto fue Gay-Lussac quien indicó
que es del orden de los −270◦ C. En 1948 William Thompon en su artı́culo “On an absolute thermometric scale”
básicamente definió:
T=t+A
en donde t viene expresada n la escala centı́grada, anotando que la escala absoluta o termodinámica de temperaturas debe ser tal que iguales adiciones de calor a un gas o cuerpo dado deberı́a corresponderle igual incremento
de temperatura. Él conocı́a la situación de su época en cuanto a que las mediciones calorimétricas revelaban que
la mayorı́a de las sustancias presentaban una variación de los clores especı́ficos con la temperatura. Sin embargo,
en los gases ideales monoatómicos, como veremos más adelante, los calores especı́ficos a volumen constante se
mantienen igual en un amplio rango y por tanto, la condición de que a iguales adiciones de energı́a térmica le
corresponden iguales incrementos de la temperatura se satisface.
Hoy en dı́a, la 13a conferencia nacional de pesas y medidas (1967-1968) etableció el Kelvin, denotado K, como
la unidad de temperatura termodinámica SI mediante:
T(K) = t (◦ C) + 273.15
2.3
(22)
Temperatura termodinámica y cinética
Si bien la termodinámica clásica tiene como objetivo la descripción e interacción de los sistemas termodinámicos
apelamos a la teorı́a cinética en su forma más sencilla, sin detalles sobre distribuciones estadı́sticas, para encontrar
una expresión de la temperatura termodinámica de un sistema sencillo en un estado de equilibrio. De acuerdo con
Bernulli supondremos que la presión de un gas ideal en tal estado de equilibrio se debe a dispersiones elásticas
de las partı́culas del gas tanto entre ellas (en el interior) como con las paredes del recipiente que lo contiene.
En la figura 5 la caja representa una partición espacial fina en el interior del gas ideal. Si queremos calcular
la presión sobre la superficie de área ∆y ∆z, perpendicular a la dirección x, tenemos que sumar sobre todas las
contribuciones de dispersiones elásticas ocurridas en un intervalo de tiempo ∆t ∼ 2∆x/v x . El factor 2 se debe a
que en la dispersión de la partı́cula tenemos un ∆x recorrido de ida y otro tanto de regreso luego de la dispersión.
P
P'
∆p x
part ∆t
∆y ∆z
(23)
en donde la sumatoria se extiende sobre todas las partı́culas que dispersan elásticamente en la pared perpendicular
al eje x, sombreada en la figura 5. En dicha figura ~pi , ~p f son los momentos inicial y final de una partı́cula debido
18
Figure 5: .
a la dispersión. En la ecuación (23) tomamos solo la componente x de dichos momentos lineales debido a que
se calcula la presión del gas sobre una pared perpendicular a la dirección del eje x. Tenemos entonces que
∆p x ∼ 2p x . Reemplazando ∆t, ∆p x en la ecuación (23) tenemos:
P
P=
px vx
∆x ∆y ∆z
part
(24)
Podemos decir, asumiendo que en dicha región del espacio con volumen ∆x ∆y ∆z, que la sumatoria es igual al
número total de partı́culas del gas en dicha región, N, multiplicado por el “promedio” del producto p x v x , denotado
hp x v x i. Ası́, si V = ∆x ∆y ∆z, la ecuación (24) es igual a:
P=
N
hp x v x i
V
(25)
Es usual llamar densidad numérica de partı́culas a la región entre el número de partı́culas del gas en la región, N,
dividida por el volumen:
P = nhp x v x i.
(26)
No entramos en detalle acerca de cómo se realiza el promedio hp x v x i que aparece en la ecuación (26). Tendremos
en su lugar las siguientes condiciones. (1) En la partición final del recipiente que contiene al gas existe un
número muy grande de partı́culas del gas. (2) En su interior el gas es homogéneo e isotrópico. Esta última
condición implica que hv x i = 0, hvy i = 0, hvz i = 0. Además las magnitudes en cada una de las direcciones deben
ser iguales en promedio. Entonces:
hv2x i = hv2y i = hv2z i.
19
(27)
Debido a la isotropı́a podemos asumir que las direcciones son estadı́sticamente independientes. Por tanto:
hv2 i = hv2x + v2y + v2z i = hv2x i + hv2y i + hv2z i.
(28)
De (26), (27), (28) vemos que (~p · ~v = pv):
1
P = nhpvi
3
(29)
P = n hp x v x i = n hmv2x i
(30)
o bien,
Ahora bien, si tenemos en cuenta tanto la idea de Bernulli (1738) de que l apresión l aejercen las partı́culas en su
dispersión (elástica), ası́ como la odea de Lambert (1777) de que cuando la temperatura absoluta (i.e. temperatura termodinámica) tiende a cero, la presión también tiende a cero, entonces vemso que esa dependencia lineal
la inferimos de la ecuación (30).
Definiendo que el promedio hmv2x i allı́ es el que nos da cuenta directa de la temperatura termodinámica del gas:
hmv2x i ≡ kB T,
(31)
en donde kB es la constante de proporcionalidad en la definición, llamada la constante de Boltzmann:
kB = 1.3806504(24) × 10−23 J K−1
(SI)
kB = 8.617343(15) × 10−5 eV K−1
Teniendo en cuenta las ecuaciones (27) y (31) vemos que:
*
+ *
+ *
+
1 2
1 2
1 2
1
mv x = mvy = mvz = kB T.
2
2
2
2
(32)
El promedio de la energı́a cinética de las partı́culas es igual entonces a (conforme a las ecuaciones 28 y 32):
*
+
1 2
3
hc i = mv = kB T.
2
2
(33)
Ası́, vemos entonces, de acuerdo con las ecuaciones (32) y (33) que por cada grado de libertad hay una contribución a la energı́a cinética media de 21 kB T ; este hecho se conoce como la equipartición de la energı́a. Mirando
la ecuación (29), teniendo en cuenta que pv = mv2 y la ecuación (33), concluı́mos que:
P = n kB T
20
(34)
Esta expresión es una forma de expresar la ecuación de estado del gas ideal. Para expresarla en la forma ampliamente más conocida, supongamos que el gas bajo estudio es homogéneo y por tanto nV es igual al número total
de partı́culas constitutivas del gas en el volumen V. Si las partı́culas son de una sola especie se puede representar
mediante N = νNA , en donde N es el número total de partı́ulas del gas bajo estuio, ν es su expresión en moles de
tal sustancia y NA es el número de Avogadro:
NA = 6.02214179(30) × 1023 mol−1
(SI)
Osea que:
N = nV = νNA
(35)
R = k B NA
(36)
Ahora bien, definamos:
en donde R es la constante de los gases o constante de los gases ideales. Su valor actualmente aceptado es:
R = 8.314472(15) J K−1 mol−1
R = 1.9858775(34) cal K−1 mol−1
De las ecuaciones (34), (35), (36) concluimos la ecuación de estado de los gases ideales:
PV = νRT
3
3.1
(37)
Primer Principio
Trabajo y energı́a
Es bien conocido en los sistemas mecánicos con describibles mediante un modelo Newtoniano que un trabajo
realizado sobre tal sistema implica un cambio en la energı́a cinética o un cambio en la energı́a potencial, o ambos
combios, tales que:
W = ∆εtotal = δεcin + δεpot
(38)
en donde W es el trabajo realizado sobre el sistema, δεcin , δεpot , δεtotal son respectivamente los cambios de las
energı́as cinéticas, potencial y total; tenemos además que: εtotal = εcin + εpot . Para que el trabajo implique solamente un cambio en la energı́a cinética el movimiento debe llevarse a cabo a lo largo de curvas situadas en
una superficie equipotencial, mientras que si el trabajo implica un cambio solo en la energı́a potencial, el trabajo
realizado debe llevarse a cabo a lo largo de un camino λ tal que en cada punto del recorridola fuerza de trabajo
sea igual en magnitud y opuesta a la que ejerce el campo de fuerzas. Tal fuerza opuesta al campo puntualmente
la denotamos F~cc (“contra el campo”,cc).
21
Figure 6: .
A modo de ejemplo calculamos la energı́a potencial de un sistema autogravitante en equilibrio hidrostático. Por
sus caracterı́sticas onsideramos que el sistema tiene simetrı́a esférica, con un radio de configuración R y masa
M. Para calcular la energı́a potencial del sistema, Ω, calculemos cuánto contribuye a la energı́a potencial del
sistema cada cascarón de masa dM(r), la cual está situada justo alrededor de una esfera interior abierta de radio
r, 0 ≤ r ≤ R, con contenido de masa M(r). La fuerza contra el campo del cascarón, al traerlo desde el infinito
hasta r viene dada por:
G M(r) dM(r)
ûr
F~cc =
r02
(39)
en donde ûr es el vector unitario en la dirección radial y r0 es la variable radial auxiliar. Ahora bien, la contribución
a la energı́a potencial del cascarón esférico es:
Z
εpot (r) dM(r) =
r
F~cc · d~s.
(40)
in f ty
En este cálculo se considera que el cero del potencial es el infinito. En cuanto al diferencial del elemento de lı́nea
d~s se tiene:
d~s = −(ds)ûr = −(−dr0 )ûr = dr0 ûr .
(41)
El elemento d~s tiene dirección −ûr porque el camino λ considera que se trae a las partı́culas radialmente desde el
infinito hasta una porción r como en la figura 6. De otro lado ds = −dr0 ya que dr0 se incrementa en el sentido
radialmente hacia el centro. Es fácil ver de las ecuaciones (39), (40) y (41) que:
22
G M(r) dM(r)
εpot (r)dM(r) = −
,
r
(42)
por tanto, teniendo en cuenta todas las contribuciones, se llega a la energı́a potencial del sistema:
Ω=−
R
Z
0
G M(r) dM(r)
.
r
(43)
Figure 7: .
Veamos ahora cómo podemos expresar el trabajo realizado sobre un gas que ocupa inicialmente una región de
volumen V1 y lo comprimimos hasta llevarlo a una situación de volumen V2 < V1 , como lo hemos ilustrado en la
figura 7. Como es un objeto extenso, debemos tener en cuenta la cantidad de fuerza por unidad de área, presión,
ejercida sobre la frontera del gas hacia su interior, y la multiplicamos por el elemento de área en cada región de la
frontera para dar cuenta de la fuerza compresora, la cual actúa en sentido contrario a d~a; ası́, el trabajo realizado
sobre el gas es igual a:
W=
Z
λ(∆R)
F~ · d~s = −
Z
p dV
(44)
∆R
en donde dV = d~a · d~s, ∆R es la región acotada por las fronteras ∂R1 y ∂R2 , las cuales encierran volúmenes V1 y
V2 respectivamente. En la ecuación (44) λ(∆R) indica un camino en el espacio de las variables termodinámicas
que describen los estados termodinámicos, para llevarlo desde un valor de volumen V1 a otro valor de volumen
V2 , en cada punto con presión aplicada p.
23
Si ahora suponemos que el proceso se lleva a cabo de manera continua a lo largo de un camino termodinámico λ,
entonces la contribución al trabajo realizado sobre el sistema cuando los puntos en cada lugar de la frontera del
sistema se desplazan cierto d~s, la denotaremos mediante dW:
dW = −p dV
24
(45)