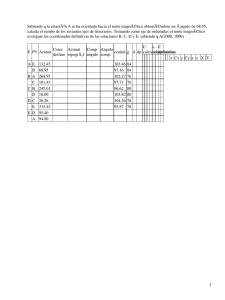
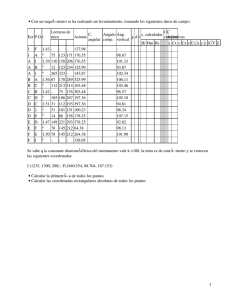
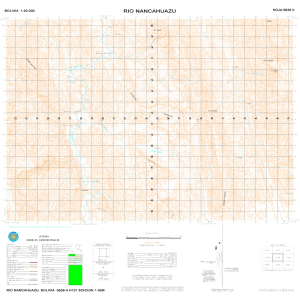
TEMA 9. Radar

Tecnología de Comunicaciones Inalámbrica ((TCI
TCI))
2012--2013
2012
TEMA 9. Radar
Juan Carlos Crespo
[email protected]
1
INTRODUCCIÓN
En este capítulo expondremos los conceptos fundamentales sobre localización de
objetos y obtención de imágenes mediante radiolocalización: radar
•
•
•
•
Cómo funciona un radar y sus limitaciones
Tipos de radar y funciones
Radares de Apertura Sintética: Alta resolución
Radares 3D
2
INDICE
9.1.
9
1 Principios fundamentales de radiolocalización –
fundamentales de radiolocalización radar (tipos)
radar (tipos)
9.2. Radares de medida de distancia en rango
9 3 Radares de medida
9.3.
Radares de medida de velocidad
de velocidad
9.4. Radar de alta resolución bidimensional (SAR)
9 5 Radar 3D: SAR Interferométrico
9.5. Radar 3D:
9.6. Ejemplo de MATLAB
3
9.1. Principios Fundamentales de un Radar
Un radar tiene por función/objeto, explorar mediante energía electromagnética su
entorno.
Al enviar radiación electromagnética no necesita un medio físico donde se propague.
propague
El siguiente esquema recoge un esquema conceptual recogiendo los componentes
básicos de un radar:
4
9.1. Principios Fundamentales de un Radar
Un radar tienen por función/objeto, explorar mediante energía electromagnética su
entorno. Para ello es necesario considerar, al menos, tres aspectos fundamentales:
-La engería enviada debe alcanzar el área o objeto a explorar con suficiente energía que
permita, después de sufrir ésta la reflexión sobre el mismo, ser recibido de vuelta por el
radar con suficiente potencia para ser detectado: ECUACIÓN RADAR
- Normalmente resulta más simple emplear radares pulsados, es decir, se envía un pulso
g , se cierra el transmisor,, y se abre el receptor
p esperando
p
recibir de vuelta la
de energía,
energía enviada. En este proceso es necesario poder distinguir a qué pulso enviado
corresponde la energía recibida: DISTANCIA AL OBJETO / RESOLUCIÓN EN
RANGO y medida de distancia en rango.
g ((Se define
f rango
g como la perpendicular
p p
a la
dirección de máxima radiación del radar)
- Capacidad para distinguir el desplazamiento en frecuencia sufrido por la onda
electromagnética, debido a la diferencia de velocidades entre el radar y el objeto
iluminado: frecuencia Doppler
5
9.1. Principios Fundamentales de un Radar
ECUACIÓN RADAR
Supongamos un antena transmitiendo un señal con longitud de onda λ con una potencia
Pt , que alcanza después de recorrer una distancia R un objeto con un coeficiente de de
reflexión (backscatter) σ , ¿qué potencia será la que se recibirá en la misma antena?
Normalmente, no se puede considerar concentrado el coeficiente de reflexión en un
único punto, por lo que se define el coeficiente de reflexión diferencial, σo como el
valor medio del coeficiente de reflexión por unidad de área, así:
6
9.1. Principios Fundamentales de un Radar
RESOLUCIÓN EN RANGO
El radar envía pulsos de duración τp cada PRI segundos (Pule Repetition Interval).
• El PRI debe ser tal que se reciba el pulso de vuelta antes del envío del siguiente
• Un pulso se extiende en el espacio
cubriendo una distancia igual a c . τp
por tanto
tanto, se podrán distinguir como
objetos distintos siempre que estos
estén separados al menos
c . τp/2 (resolución en rango)
z
recepción
emisón
τp
c τp
PRI
El tiempo que se tarda en recibir la
señal de vuelta determina la distancia:
c . T /2
Siendo T el tiempo de ida y vuelta
de la señal o retardo.
“el
el flanco anterior del eco del
objeto más distante debe llegar al
receptor más tarde que el flanco
posterior del eco del objeto más
cercano”
H
c τp
δr = c τp/2
y
7
9.1. Principios Fundamentales de un Radar
RESOLUCIÓN EN RANGO
Esquema conceptual de bloques de un radar pulsado.
Siendo T, representa el retardo y A la modificación
global del pulso en enviado: reflexión y atmósfera,
atmósfera el
pulso recibido:
p
la ecuación radar se debe obtener una energía
g
Aplicando
recibida suficiente a partir de la energía transmitida:
Pt(w) . τp
Debido a que en envío de pulsos suficientemente estrechos y con energía suficiente es
difícil tecnológicamente, se emplean en muchas casos pulsos modulados.
8
9.1. Principios Fundamentales de un Radar
FRECUENCIA DOPPLER,
DOPPLER MEDIDA DE VELOCIDAD
El radar envía una onda electromagnética con frecuencia central fc, y recibe la energía
enviada modificada por el coeficiente de reflexión y desplazada en frecuencia fD
(frec encia Doppler).
(frecuencia
Doppler) A partir de la fD es posible obtener la diferencia de velocidades
elocidades
entre ambos: radar y objeto iluminado. El retardo temporal entre el pulso enviado y el
recibido no es relevante.
Donde uR es la
velocidad en la
dirección R
9
9.1. Tipos de Radares
• Unidimensionales:
-Medida de Distancia en rango: pulsados (ya vistos) y Chirp
-Medida
Medida de velocidad
elocidad
• Bidimensionales – teledetección
• Tridimensionales – levantamiento de Terreno (DTM: Digital Terrain Model)
10
9.2. Ejemplo: Radar pulsado c/s Chirp
• Unidimensionales:
- Radar pulsado con y sin modulación (Chirp)
Geometría General
El se desplaza a velocidad , V, en línea recta y altura, H
(constantes).
La antena apunta lateralmente de forma que su haz sea
perpendicular a la trayectoria y dirigido hacia tierra plana.
Ejes de coordenadas, acimut, en la dirección de vuelo, y rango,
dirección del máximo del diagrama de radiación de la antena.
La mínima distancia en rango en el plano de visión como: Ro, y
que, al depender de rango, en general se representará por la
función Ro(r).
Z
Lr
θl
R
o
H
R
Se define el ángulo de apuntamiento (look angle,θ l) como el
ángulo delimitado por la recta del máximo del lóbulo principal
de la antena y la vertical.
θa
θi
X
Y
El ángulo de incidencia, θ i, se define como el comprendido
entre la normal a la superficie de la tierra en el punto de interés
y la recta del máximo del lóbulo principal de la antena (si la
tierra es plana ambos coinciden)
11
9.2. Ejemplo: Radar pulsado c/s Chirp
recepción
emisón
• Unidimensionales:
- Pulsados
Resol ción en Rango
Resolución
τp
PRI
La resolución en rango, δr, vendrá limitada por la duración de los pulsos emitidos, τp.
Lógicamente, para poder discriminar dos objetos situados en la misma dirección en rango,
es necesario
i que ell flanco
fl
anterior del
d l eco del
d l objeto
b
más distante
d
ll
llegue
all receptor más
tarde que el flanco posterior del eco del objeto más cercano. Así la resolución en rango en
el plano de visión del radar se puede expresar como:
δr = cτp / 2
que expresa la separación mínima entre dos curvas equitemporales
Caso de ángulo de
incidencia θi pequeño
Caso de ángulo de
incidencia θi grande
θi
θi
δr
δr
δrt
Poca Resolución
sobre el terreno
superficie
fi i
Debido a la geometría, para
una misma resolución en el
plano de visión, dr, la
resolución que se obtiene sobre
el terreno varía con el ángulo
de incidencia
incidencia, qi, empeorando
cuanto menor sea éste, como
puede apreciarse en
δrt
Buena Resolución
sobre el terreno
12
9.2. Ejemplo: Radar pulsado c/s Chirp
• Unidimensionales:
- Resolución en Rango - Modulación
Si la duración de los ppulsos emitidos pudiera
p
hacerse arbitrariamente estrecha,, se podría
p
elevar la resolución en rango tanto como fuese necesario, sin embargo, a medida que se
disminuye la anchura del pulso, es necesario aumentar la potencia de pico enviada para
mantener la potencia media en valores razonables, y así, obtener una relación señal/ruido
(Signal to Noise Ratio,
Ratio S/R) aceptable,
aceptable por lo que pronto se llegaría a un límite tecnológico.
tecnológico
Como se verá, una solución al problema es introducir una modulación en el pulso emitido y
realizar posteriormente su compresión. Con esta técnica es posible alcanzar resoluciones
en rango
g aceptables
p
sin degradación
g
del margen
g de S/R.
τ
τp
fc
τ
Br
La modulación habitualmente
empleada es la modulación lineal en
frecuencia, FM. Al pulso enviado se
denomina comúnmente pulso "chirp”
La resolución ya NO es función del
ancho del pulso sino de su ancho de
banda (B):
δr = c
2B
τp
13
9.2. Ejemplo: Radar pulsado c/s Chirp
La frecuencia el pulso enviado crece
linealmente con la frecuencia, de la misma
f
forma
ell recibido.
ibid Sii se hace
h
pasar por un ffiltro
l
que retarda la señal linealmente en función de
la frecuencia, entre f1 y f2, teóricamene la señal
en el tiempo tendría una anchura τp cero.
En la práctica, debido a que la diferencia entre
f1 y f2 es finita
fi i (finito
(fi i ell B),
B) se produce
d
un pulso
l
“comprimido con forma de sen(x)/x , i.e.:
sinc(x), cuya anchura se aproxima por 1/B
14
9.3. Ejemplo medida velocidadvelocidad- Doppler
• Unidimensionales:
-Medida de velocidad - Doppler
Z
La frecuencia Doppler se puede expresar, para
ángulos pequeños (<30º) y considerando el
recorrido de ida y vuelta de la señal radar,, como:
fD = - (2V/λ) senθα(t)
Donde θα(t) , representa el ángulo formado
entre
t la
l perpendicular
di l a la
l línea
lí
d vuelo
de
l y la
l
recta que une el radar y el punto observado en
función del tiempo en acimut, t. Aproximando el
seno ppor el ángulo
g
y el desplazamiento
p
ppor el
arco, podemos expresar la frecuencia Doppler
como:
fD = - 2(V/λR)x
H
Δθ
θ
R
x2
X
R
x1
Y
Δ x
Así, la frecuencia Doppler inducida por un punto
situado en x1, será, - 2(V/λR)x1, mientras que la de
otro en x2, situado a igual distancia en rango e
iluminado por el haz radar en el mismo instante,
sería
í de
d -2(V/λR)x
2(V/λR) 2
15
9.3. Ejemplo medida velocidadvelocidad- Doppler
• Unidimensionales:
U idi
i l
-Medida de velocidad - Doppler
Si sólo existiera un “blanco/punto” que
produzca
d
d l
desplazamiento
i t
D l
Doppler,
su
velocidad se puede obtener como se vio en la
transparencia 9.
curvas equidoppler
curvas equitemporales
-f
En la
E
l práctica
á ti hay
h “infinitos
“i fi it puntos”,
t ” por lo
l
que habrá que buscar cómo separar las
variaciones en frecuencia que producen cada
uno siempre
p qque sean separables.
p
El lugar geométrico de los puntos que
producirían un mismo desplazamiento Doppler
es una hipérbola en el plano XY, resultado de
l intersección
la
i t
ió de
d conos coaxiales
i l cuyo eje
j es
la trayectoria y dicho plano:
-f
f1
1
t
2
t
f
2
2
1
X2[(2V / lfD)2-1]
1] - y2 = H2
16
área iluminada
9.4. Ejemplo Bidimensional: Apertura Sintética
• Bidimensional:
Bidi
i l
Radar de visión lateral SAR
- Resolución en rango:
g en función de la modulación / ancho de banda del ppulso comprimido
p
(igual que el caso de radar en rango con modulación)
- Resolución en acimut: en función del ancho de banda Doppler
La resolución
l ió en acimut
i
máxima
á i alcanzable,
l
bl es
función del ancho de banda Doppler, BD. Éste vendrá
dado por la diferencia entre las frecuencias Doppler
máxima, fDmax
, y mínima, fDmin
D
D i . Las frecuencias
Doppler máxima y mínima se alcanzarán para cada
punto del terreno cuando éste esté iluminado por los
extremos del haz radar (i.e., separados θa, apertura
angular
l de
d la
l antena real).
l)
(donde fc representa la frecuencia de la portadora).
Así:
Z
θa
Y
BD ≈ (2V/λ) [sen(θa/2) - sen(-θa/2)]
fc
BD ≅ 2V / La
La: Longitud de la antena en la dirección de vuelo
( i t)
(acimut)
fc + fDmin
r
X
fc + fDmax
17
9.4. Ejemplo Bidimensional: Apertura Sintética
• Bidimensional:
Bidi
i l Resolución
R l ió en acimut
i
• La longitud de la apertura sintética máxima sintetizable, LA, viene limitada por la
necesidad de que un mismo objeto debe ser captado por la antena radar durante todo el
tiempo
i
que en que ésta
é dure,
d
es decir,
d i la
l apertura máxima
á i sintetizable
i
i bl seráá de:
d
LA(r) = Ro(r)⋅θa
Resolución máxima en acimut. La
resolución en acimut, δa, en función de la
capacidad de discriminación en frecuencia
Doppler, resolución Doppler, δfD , se expresa
como:
Z
LA
δa = (λR / 2V)δfD
θa
La
Ro(r)
θA
Y
La resolución máxima en frecuencia será la
inversa del tiempo de observación[1], TA, tiempo
en que un objeto permanece iluminado, es decir
el tiempo en que el radar recorre la longitud de
su apertura sintética, así: TA = R θa / V = R λ / La V = 1/δfD
y por tanto:
δa = (λR / 2V) (La V / R λ )
δa = La / 2
X
¡Resolución que aumenta a medida que
disminuye la longitud de la antena[2] en acimut
e independiente de la distancia y de la
18
longitud de onda!
9.4. Ejemplo Bidimensional: Apertura Sintética
• Bidimensional:
Bidi
i l Respuesta
R
a un Blanco
Bl
Puntual
P
l (rango)
(
)
Cada pulso de la señal enviada, para una portadora de
frecuencia fc tendrá la forma:
ss(t, t) = a(t) Π(t) exp[j2π(fc+kt)t]
-B /2
B/2
A m plitud
τ
-1/B
-3/B
-2/B
0
1/B
2/B
3/B
Donde:
τp
• t, representa el tiempo en dirección del rango (retardo en rango), reservando t para el tiempo
en la dirección del desplazamiento del CFA, acimut.
• a(t), representa el diagrama de radiación de la antena que es considerado localmente
constante para cada t y t.
• Π(t), representa un pulso rectangular que consideraremos centrado en t = 0 y de duración tp.
• k , es ell factor
f
de
d modulación
d l ió lineal
li l en frecuencia
f
i (chirp
( h rate).
) D
Dependiendo
di d ddell signo
i
de
d k,
k
se tendrá un crecimiento en frecuencia (up-chirp) o decrecimiento (down-chirp).
Nota: La doble notación en minúsculas para la señal, ss(⋅), se ha escogido para denotar
que es una señal bidimensional y representada en ambas dimensiones (rango y acimut) en
el dominio del tiempo
9.4. Ejemplo Bidimensional: Apertura Sintética
• Bidimensional:
Bidi
i l Respuesta
R
a un Blanco
Bl
Puntual
P
l (acimut)
( i
)
Calculemos la evolución de fase de un blanco. Al recorrer el radar su apertura sintética. Nótese
cómo la variación de R fuerza que la fase de la señal llegue retrasada.
Z
si R(t) es la distancia al blanco y Ro, la distancia
mínima a éste,
éste entonces,
entonces la fase de la señal enviada
en iada
2
2
Δφ(t)
≈ (2π / λ) (Vde
t /ida
Ro) y vuelta) de:
sufrirá un retraso
(recorrido
q ppresenta una evolución cuadrática de la fase
que
respecto al tiempo en acimut, es decir lineal en
frecuencia.
Se observa que la evolución de fase en acimut
anteriormente calculada es similar a la introducida (por
diseño) en rango si se emplea modulación FM.
H
Ro
R
X
Y
R2(t) = Ro2 + (Vt)2
R(t) ≈ Ro + (Vt)2/2Ro + …
9.4. Ejemplo Bidimensional: Apertura Sintética
La señal, así retrasada y modulada por la reflectividad del terreno, es recibida por el radar. En el
receptor la señal recibida se suma coherentemente con la señal de referencia del receptor (generada
por un oscilador local en fase) para su demodulación. Así, cuando ambas están en fase (diferencia de
fase: 0,
0 2π,
2π 4π,
4π ...),
) se alcanzará un máximo de la señal resultante,
resultante mientras que cuando están en
contrafase (π, 3π, 5π, ...) se tendrá un mínimo.
T ie m p o e n a c im u t, t
Representado en ordenadas la evolución
cuadrática de la fase de la señal recibida
(antes de la demodulación) respecto al tiempo
en acimut o el espacio recorrido por el radar
durante su apertura sintética (abcisas).
8π
6π
4π
2π
Mientras que en la parte inferior, se ha
representado la amplitud de la señal después
de su demodulación (resultado de la suma
coherente que tiene lugar en el demodulador).
Observándose nuevamente de forma gráfica
la variación lineal del periodo de la señal
recibida con t.
E s p a c io re o c o rrid o e n a c im u t, x
21
9.4. Ejemplo Bidimensional: Apertura Sintética
• Bidimensional:
Bidi
i l Respuesta
R
a un Blanco
Bl
Puntual
P
l (rango
(
y acimut)
i
)
La modulación sufrida en acimut por la señal radar es similar a la modulación chirp en rango.
Por ello todo lo expuesto para la primera también es de aplicación a la segunda. Así, la respuesta
de un blanco puntual en ambos ejes tendrá la misma forma.
• Acimut: Por ello si se registrase la respuesta, procedente de un blanco puntual, ésta dejaría un
"rastro" en acimut (señal bruta recibida) cuyas intensidades seguirían una función sen x/ x.
• Rango: se tendría un comportamiento similar.
similar Así,
Así si representáramos la respuesta puntual en
un plano (acimut-rango), la respuesta global sería la composición de ambas
ra
ango
Acimut
• Resolución en rango ~ 0’5 m
• Resolución en acimut ~ 0’15 m
22
9.4. Ejemplo Bidimensional: Apertura Sintética
• Bidimensional:
Bidi
i l V
Variación
i ió dde lla modulación
d l ió en acimut,
i
migración
i
ió en rango
La evolución de fase de un blanco depende de r, distancia en rango, y ésta varía de rango cercano a
rango lejano cubriendo toda la imagen en ese eje. Así pues, cuanto mayor sea r, mayor es el tiempo de
observación y mayor será la extensión temporal de la respuesta del blanco.
blanco
La modulación inducida en rango, depende fuertemente del rango, es decir se induce una modulación
que depende del rango.
Se ppuede observar la variación de la apertura
p
sintética en el pplano de visión. Igualmente,
g
en las figuras
g
se ha representado la señal tras la demodulación y en amplitud, que se obtendría de dos blancos
puntuales situados a diferentes distancias en rango: R1 y R2 / R2 = 2R1.
V
A p ertu
t ra ra ng o cerca no
Respuesta en amplitud del blanco r1
1
Respuesta en amplitud del blanco r2
2
23
A p ertura ran go le jan o
9.4. Ejemplo Bidimensional: Apertura Sintética
• Procesado: Técnica de Compresión en el tiempo y dominio de la frecuencia (rango
y acimut)
La extracción de σ (imagen del objeto) de la señal recibida se podría realizar en el
tiempo (espacio de la señal),
señal) mediante dos correlaciones cruzadas,
cruzadas una para
comprimir la señal dispersa en rango y otra para la compresión de la señal dispersa
en acimut. Estos procesos, sin embargo, resulta más eficiente realizarlos en el
dominio de la frecuencia
•
ϕ(t)
pa(t)
( ) = ϕ(t)
ϕ( ) * h (t)
( ) ; donde
d d “*”
* representa ell operador
d convolución.
l i Es fácil
f il
demostrar que la compresión en máxima cuando h(t) = ϕ* (t)
ϕ* ((t))
pa(t)
pa ( t ) =
TA / 2
∫
φ (t + s )φ * ( s )ds
−T A / 2
24
9.4. Ejemplo Bidimensional: Apertura Sintética
C
Compresión
ió de
d un pulso
l Modulación
M d l ió intrapulso
i t
l LFM ( T=10
T 10 μseg, B = 100 Mhz)
Mh )
pa (t ) =
TA / 2
∫ exp[2πj (φ t + φ t
1
2
2
]
/ 2) exp[2πjφ 2ts ]ds
−TA / 2
p a (t ) = {termino de fase}
PSLR =
- 13.26
13 26 dB
sen(πφ 2TAt )
πφ 2TAt
δr =
c
2B
•
Aprovechando propiedades de la transformada de Fourier
pa(t) = TF-1 [ ϕ(f). ϕ* (f)]
Para procesar basta “comprimir la señal” tanto en rango como en acimut.
1)) FFT
2) Multiplicación (complejo conjugada de la función de referencia)
3) IFFT
25
9.4. Ejemplo Bidimensional: Apertura Sintética
• Procesado: Diferencias entre rango y acimut
• Rango
Z
Parametros conocidos e invariantes
• Acimut
θ sq
Existencia de Migración en Rango y curvatura
variable con el rango
Falta de ortogonalidad de las coordenadas SAR
fuera del cero Doppler
Variación de los parámetros Doppler
H
Ro
Rc
R
tc
Necesidad de:
" FILTRO DE COMPRESION DIFERENTE PARA
CADA PUNTO"
X
Y
26
9.4. Ejemplo Bidimensional: Apertura Sintética
• Bidimensional:
Bidi
i l toma de
d imagen
i
bruta
b
– espacio
i de
d la
l señal
ñ l
• Estudiemos primero la estructura de la señal recibida. Empleamos una geometría real,
donde existe una desviación respecto a la perpendicular al vuelo, θsq
Señal bruta (espacio de la señal)
t
c.τp
1 / PRF
2Ro/c
τ
El conjunto de ecos radar muestreados pueden ser
almacenados de forma natural como un bloque
bidimensional de muestras ordenado y referido a los
ejes acimut y rango. Dicho orden representa una
referencia temporal relativa al comienzo de la toma
de imagen y al retardo al primer punto en rango para
cada eco.
Retardo relativo
PRI
τp τv
Τv
fijos durante la toma de imagen
1/ Fm
9.4. Ejemplo Bidimensional: Apertura Sintética
• Procesado: Compresión en el dominio del tiempo versus dominio de la frecuencia
• Compresión en el dominio del tiempo
• Flexible, permite una función de compresión diferente para cada punto
• GRAN CARGA COMPUTACIONAL: e.g. Compresión de una señal de
longitud L y función de referencia de longitud M
==> Se requieren 2LM operaciones complejas
(M=1000, L=2048 ==> 4 Millones de oporeaciones Complejas)
• Requiere interpolaciones costosas (e imprecisas) para selección de puntos
con información del blanco (migración en rango)
• Compresión
C
ió en ell dominio
d i i de
d la
l frecuencia
f
i
∞
g (t ) =
∫
f * (t )h(t + s )ds
G(w) = F*(w)H(w)
−∞
• Compresión de una línea cada vez:
Si el ancho de banda de las modulaciones FM sufridas por la señal SAR se
pueden considerar acotadas y a que los parámetros que las definen no varían
de forma brusca, el espectro correspondiente a dos o más puntos de una misma
línea (acimut) o columna (rango) son similares.
• EFICIENTE: e.g. Compresión de una señal de longitud L y función de
referencia de longitud M
==> Se requieren L+3Llog2(L) operaciones complejas
(M=1000, L=2048 ==> 69.632 de operaciones Complejas)
28
9.4. Ejemplo Bidimensional: Apertura Sintética
• Procesado: Compresión en el dominio de la frecuencia
frecuencia, facilita la corrección de la
migración en rango de la señal en acimut
τ
Domino
del tiempo
τ
t
acimut
Domino
rango Doppler
rango-Doppler
fDmin
0
acimut (Doppler)
fDmax
fa
29
9.4. Ejemplo Bidimensional: Apertura Sintética
• Bidimensional:
Bidi
i l Influencia
I fl
i de
d los
l errores de
d movimiento
i i
• Estudiemos primero la estructura de la señal recibida. Empleamos una geometría ideal
donde no existe una desviación respecto a la perpendicular al vuelo, θsq
Señal bruta (espacio de la señal)
t
c.τp
1 / PRF
rango
2Ro/c
τ
Retardo relativo
Acimut
•En rango, la modulación es controlada por diseño
•En acimut, la modulación es inducida, depende de la geometría, y en
particular de la variación de R(LOS), y sus derivadas.
9.4. Ejemplo Bidimensional: Apertura Sintética
• Procesado: Influencia de los errores de movimiento
No se considera sistemas de CM en tiempo real
Ventana de recepción en posición fija
Antena NO estabilizada
Errores entre pulso y pulso
SITUACION MAS GENERAL
Z
dirección de imagen
θ sq
máximo de radiación
trayectoria CFA
H
Ro
acimut
Rc
R
tc
X
Y
31
9.4. Ejemplo Bidimensional: Apertura Sintética
• Procesado: Influencia de los errores de ACTITUD
Efecto principal: variación Doppler
Efectos añadidos:
Errores en amplit
amplitud
d o mod
modulaciones
laciones en amplit
amplitud
d
Errores geométricos
Z
z
DERIVA
GUIÑADA
V
ALABEO
X
CABECEO
X
Y
Alabeo:
Cabeceo:
Deriva y guiñada:
θ r (t ) = θ r + Δθ r (t )
Y
θ p (t ) = θ p + Δθ p (t )
θ dj (t ) ≈ θ d + Δθ j (t )
Todos,
T
d a excepción
ió del
d l alabeo,
l b suponen un desplazamiento
d l
i
d la
de
l frecuencia
f
i
en acimut (frecuencia Doppler), desplazamiento que es, en general,
dependiente del rango, r.
32
9.4. Ejemplo Bidimensional: Apertura Sintética
• Procesado: Error de actitud (ALABEO)
SITUACIÓN NOMINAL EN RANGO
Bp
¡Unico que no desplaza el espectro!
Error en amplitud en rango (parte constante)
Modulación en amplitud en acimut (parte variable)
No existe error geométrico
ALABEO
Ganancia de ida y vuelta,
relativa a la del máximo de
radiación, se puede modelar en
tensión para cualquier ángulo
z
τ
0
3 dB
V
−K
real
nominal
a (t ) =
a
e
⎛
⎜
⎜
⎜
⎜
⎜
⎝
θ
2
⎞
( t ) ⎟⎟
2
θ
3 dB
⎟
⎟
⎟
⎠
SITUACIÓN CON ALABEO
Tv
, con Ka ≈ 22'77
77
X
Y
Un error constante en θr(t), produce una error en
ganancia
i variable
i bl para cada
d rango pero constante
t t en
acimut. Sin embargo la parte variable, Δθr, induce
una modulación de la intensidad de la señal en
p
ecos pares
p
emporando
p
el PSLR.
acimut qque produce
2K ⎞
Δa ⎛
= ⎜⎜θ r (t ) 2 a ⎟⎟Δθ r
θ 3dB ⎠
a ⎝
Δθ r =
2θ 3dB 1
K a PSLR
0
3 dB
33
9.4. Ejemplo Bidimensional: Apertura Sintética
• Procesado: Error de actitud (CABECEO)
CABECEO
z
Desplazamiento del espectro Doppler
Error constante en amplitud y/o modulación en amplitud
Error geométrico en acimut y rango
V
ERROR DE AMPLITUD EN ACIMUT (RANGO CERCANO)
X
Pa(f)
Bp
CABECEO
Vx
Y
X
f
-f D 0
CABECEO
αTv
ERROR DE AMPLITUD EN ACIMUT (RANGO LEJANO)
V
Vx
X
Pa(f)
Bp
Y
ERROR EN AMPLITUD EN RANGO
-f D
0
f
ERROR EN GANANCIA EN ACIMUT,
POR VARIACIÓN ESPECTRO DOPPLER
Δθ p =
θ 32dB
1
K aθ p PSLR
Y
ERROR GEOMETRICO
9.4. Ejemplo Bidimensional: Apertura Sintética
• Procesado: Error de actitud (DERIVA Y GUIÑADA)
Lo consideraremos compuesto por su parte constante, θd, y su parte variable Δθj(t): θ dj (t ) ≈ θ d + Δθ j (t )
Produciendo una rotación del diagrama de radiación de la antena alrededor del eje vertical.
DERIVA Y GUIÑADA
z
Desplazamiento del espectro Doppler
Error constante en amplitud y/o modulación en amplitud
Error geométrico en acimut y rango
AMPLITUD NOMINAL EN ACIMUT (SIN ERROR)
Pa(f)
V
Bp
Vx
X
X
Y
f
0
ERROR DE AMPLITUD EN ACIMUT
Vx
Pa(f)
X
Y
Bp
ERROR EN AMPLITUD EN RANGO
Δθ j =
f
-fd
θ 32dB
1
K aθ d PSLR
Y
0
ERROR EN AMPLITUD DEBIDO A
VARIACION ESPECTRO
DOPPLER
ERROR GEOMETRICO
9.4. Ejemplo Bidimensional: Apertura Sintética
• Procesado: Los errores de movimiento al menos tienen que tenerse en cuenta
porque influyen en la Variación Doppler
Frecuencia Doppler central
¡Factor de modulación !
Estructura de la señal bruta
Varia ancho de banda Doppler
R
Resolución
l ió máxima
á i
f D (t, r ) = −
z
BD =
2V (t )
λ
sen θ sq (t ; r )
⎛θ ⎞
sin⎜ 3dB ⎟ cos(θ sq )
λ
⎝ 2 ⎠
− 4V
V
− 2V 2
f dr ≈
cos 2 (θ sq )
λRo (r )
X
SQUINT
δa ≈
Δφ (t ; r ) =
πBDTA Δf dr
4
f dr
λ
1
La
≈
2 θ 3dB cos(θ sq ) 0'89 * 2 * cos(θ sq )
Y
¡Los principales efectos de errores de actitud
pueden ser englobados en el ángulo de
squint!
CORRECCION EN PROCESADO
CONSIDERACION EN CADA PASO
sen (θ sq ) = sen (θ l ) ⋅ sen θ djd + cos(θ l ) ⋅ sen p (θ p )
PASO DE CALIBRACION (C
(Corrección
ió radiométrica)
di ét i )
36
9.4. Ejemplo Bidimensional: Apertura Sintética
• Procesado: Errores de Traslación
PROBLEMA : ¿RELACION ENTRE LOS ERRORES DE TRASLACION Y SUS EFECTOS?
Error en amplitud (relativo o absoluto)
ERROR DE FASE (relativa)
VARIACION DE LA MR (relativa)
METODO:
1) Evaluación de los errores de fase
(¡con squint!) en la imagen
Z
2) Obtener los errores de fase que implica
cada error de traslación significativo
(velocidad, ...) ==> desarrollo en serie R(t;r)
θ sq
PROBLEMA ADICIONAL: ¿QUE ERRORES SON SIGNIFICATIVOS?
Δy(t)
Δz(t)
⎧⎪⎛ x(t ) − x ⎞ 2 ⎛ Δy (t ) ⎞ 2 ⎛ Roy ⎞ 2
Δy (t )Roy
o
⎟⎟ + ⎜⎜
⎟⎟ + ⎜⎜
⎟⎟ − 2
Re (t ) = Ro ⎨⎜⎜
+
Ro2
⎪⎩⎝ Ro ⎠ ⎝ Ro ⎠ ⎝ Ro ⎠
Δx(t)
H
Ro
2
Re(t)
R(t)
Re (t ) = Ro
Rc
2
2
⎛ V t + ΔV (t ) dt − xo ⎞
∫
⎜
⎟ − 2 Δy (t ) Ro − H + 2 Δz (t ) H + 1
⎜
⎟
Ro
Ro
Ro
Ro Ro
⎝
⎠
tc
to
¡SOLO LOS CONTENIDOS EN EL PLANO DE VISION DEL RADAR!
R oy
En particular:
t
X
xo
Y
rLOS (t ) = Δy (t )sen (θ l ) + Δz (t ) cos(θ l )
V (t )
37
9.4. Ejemplo Bidimensional: Apertura Sintética
• Procesado: Corrección de Erorres
Necesidad
Necesidad de
de corregir:
corregir:
Variación de velocidad (geométricos y fase)
Los desplazamientos
p
en LOS y sus derivadas (función
(
de la apertura)
p
)
Los errores de fase inducidos
Errores radiométricos debidos a los errores anteriores y de actitud
Conclusiones:
No es posible la corrección de V(t) sin antes corregir el
desplazamiento en LOS
La variación de fase debida a V(t) es dependiente del
punto a enfocar (¡error residual si se corrige el LOS antes
de la velocidad!)
No es posible corregir el error en LOS exactamente antes
de la compresión en rango
La corrección en LOS debe constar de dos pasos:
desplazamiento y fase (por ello no deben ser separados
en general)
Las correcciones de V(t), LOS y fase deben realizarse
antes de la compresión en acimut
La corrección de la MR se realiza de forma natural al
corregir los errores de V(t), LOS y fase
Error en LOS
Señal bruta almacenda
Acimut
traza asumida de la historia en acimut de un
blanco , si no se tiene en cuenta el error LOS
traza real de la historia en acimut de un blanco ,
teniendo en cuenta el error LOS
38
9.4. Ejemplo Bidimensional: Apertura Sintética
Sección de la imagen en Banda X polarización VV con CMdS, del aeropuerto de
Dornier en Oberpfaffenhofen
p
((Munich))
En la imagen la dirección de acimut corresponde a las abcisas y la dirección rango
corresponde a ordenadas. La resolución en rango es de 3 m (≈ 4'41 m debido al
enventanado
t d Hamming
H
i 0'54),
0'54) mientras
i t que lla resolución
l ió en acimut
i t procesada
d es de
d 1
m (1'47 debido al enventanado Hamming 0'54. El ángulo de squint medio: qsq ≈ 3'5º, que se ha considerado igual y constante para el procesado.
39
9.4. Ejemplo Bidimensional: Apertura Sintética
Sección de la imagen en Banda X polarización VV con CMdS,
CMdS del aeropuerto de
Dornier en Oberpfaffenhofen (Munich). PARÁMETROS TÉCNICOS:
Banda X (fo)
9’6 GHz
en
19º / 33º
Retardo a la 1ª muestra
18'5 μsg
Apertura
acimut/rango
i t/
Velocidad nominal
75'02 m/sg
Duración del pulso
Ancho de banda, B
Espaciado en rango
5 μ sg
50 MHz
1'5 m
Resolución acimut
Resolución rango
Squint medio
1'0 m
3’0 m
3’4879 º
952'381 Hz
----571'0 m
Hamming Acimut
Hamming Rango
Nº de subimágenes
0'54
0'54
1
PRF
Presumming
Altura media terreno
40
9.4. Ejemplo Bidimensional: Apertura Sintética
• Procesado: Medidas de calidad
Medias y desviaciones típicas de la resolución (los 5 conos) –
Blancos puntuales:
• PSLR: peak side lobe ratio
• ISLR: integrated side lobe ratio
res (m)
ISLR
PSLR
media acimut
1.54478
-19.661
-14.673
σ acimut
0.01347
0.56492
0.63483
media rango
4.7656
-22.038
-16.661
σ rango
0.01493
1.03540
0.92933
PSLR
ISLR
41
9.5. Ejemplo tridimensional: SAR Interferométrico
Se emplean dos antenas …
S1
Bd
ξ
S2
•
θ
•
R1
•
H
R2
•
Modos de funcionamiento:
Simple
Sól una Tx y Rx las
Sólo
l dos
d
Simple secuencial
Sólo una Tx y Rx primero una y después la otra
Dual
Tx primero una Rx ella misma, después Tx la otra
y recibe ella misma
Doble
T una y Rx
Tx
R las
l dos,
d después
d
é la
l otra Tx
T y Rx
R las
l dos
d
h
y
Bd, es la longitud de la línea de base
R1, es el rango del blanco a la antena 1
R2, es el rango del blanco a la antena 2
ΔR, es la diferencia de espacio recorrido, i.e., R2-R1
H, es la altura de vuelo sobre suelo plano medida sobre la antena 1
θl, es el ángulo de apuntamiento medido desde la antena 1
ξ, es el ángulo de inclinación de la línea de base
h, es la altura del objeto apuntado sobre el suelo
x, es la proyección sobre el plano de tierra la línea de vuelo
42
9.5. Ejemplo tridimensional: SAR Interferométrico
• Procesado: Obtención de la altura
De la geometría se tiene que la altura h, se puede obtener mediante:
h = H − R1 cosθ l
y a su vez, la diferencia de espacio recorrido se puede obtener a partir de la fase de la
diferencia de fase de las señales recibidas por ambas antenas, mediante:
{
}
h = H − R1 cos ξ 1 − sen 2 (θ l − ξ ) − sen ξ sen(θ l − ξ )
Donde (θl-ξ), representa el ángulo de incidencia local, que puede calcularse a partir de la
diferencia de espacio recorrido por la señal recibida por ambas antenas, mediante:
sen(θ l − ξ ) =
(R
1
+ ΔR ) − R 2 − Bd 2
2 R1 Bd
y a su vez,, la diferencia de espacio
p
recorrido se ppuede obtener a ppartir de la fase de la
diferencia de fase de las señales recibidas por ambas antenas, mediante:
Δφ= -d
2π
λ
⋅ ΔR
Nótese que d, únicamente representa un factor 1 ó 2, dependiendo del modo de actuación del
InSAR, en el caso de InSAR de pasada doble o en el caso de que se el modo dual
43
9.5. Ejemplo tridimensional: SAR Interferométrico
• Procesado: Ejemplo
Volcán Kīlauea (uno de los volcanes más grandes del
planeta y uno de los cinco volcanes que forman la isla de
Hawai))
Data acquired on April 13, 1994 and on October 4, 1994 from the
X-band Synthetic Aperture Radar on board the space shuttle
Endeavour were used to generate interferometric fringes, which
were overlaid on the X-SAR
Diferencias de fase: Interferograma
DTM superpuesto con Imagen SAR
Tecnología de Comunicaciones Inalámbrica ((TCI
TCI))
2012--2013
2012
TEMA 9. Radar
Juan Carlos Crespo
[email protected]
45