Hoja de problemas 3 Multimedia. Soluciones.

Hoja de problemas 3 Multimedia. Soluciones.
Compresión sin perdidas. 0.3 puntos.
1)Comprimir, utilizando BWT, R2F y RLE en este orden la siguiente
cadena aaaabbccaaaabbcc...aaaabbcc, donde el numero de repeticiones de
aaaabbcc es 1000.
Un escript que resuelve el problema codificando la trasformada de BWT
a RLE:
awk ’BEGIN{printf("@"); for(i=0;i<1000;i++) printf("ccbbaaaa"); printf("\n");}’\
| # generar cadena inversa \
awk ’{for(i=1;i<=length($0);i++) printf("%s\n",substr($0,i)substr($0,1,i-1));}’\
| # rotaciones \
sort \
| # ordenar \
awk ’{printf("%s\n",substr($0,length,1));}’ \
| # imprimir solo el ultimo caracter de las rotacion \
awk ’{if (a!=$0) { print k,a; a=$0; k=0;} k++;}END{print k,a;}’ \
#imprimir run length
El resultado de la ejecucion del script:
4
1000
2997
1000
2000
999
1
a
b
a
b
c
a
@
Lo que significa a4 b1000 a2997 b1000 c2000 a999 @1 , donde el subindice significa
el numero de repeticiones de la letra correspondiete.
R2F y RLE empenzado con alfabeto {a, b, c, @}:
04 11 0999 11 02996 11 0999 21 01999 21 0998 31
2) Comparar el resultado con compresión LZ. El LZ se puede calcular a
mano o con el escript en el apendice A. Aplicando el escript:
awk ’BEGIN{ for(i=0;i<1000;i++) printf("aaaabbcc"); printf("\n");}’ | \
awk -f lz0.awk
1
tenemos:
0
3
1
1
7991
0
1
1
1
8
’a’
’b’
’c’
’a’
EOF
En comparación del BWT en este caso el codigo LZ es más corto.
Transformada de Fourier y DCT. 0.7 puntos.
Dadas las señales
h = {3, 3, 4, 1, 0, −1, −2, −7} y g = {3, 5, 5, 3, 3,1, 1, 3}
1) Hacer la transformada de Fourier de 8 puntos.
2) Hacer la transformada DCT de 8 puntos sobre ellos (precisión 2
dı́gitos).
3) Conservar sólo 4 de los 8 cocientes independientes de cada transformada, correspondientes a las frecuencias mas bajas de la señal.
4) Hacer las transformadas inversas de las transformadas FT y DCT
solo con los 4 componentes independientes. Los resultados les denominamos
h0F T ≡ F −1 [Restingir4comp.[[F [h]]], h0DCT ≡ DCT −1 [Restringir4comp[DCT [h]]],
idem g.
5) Representar las señales originales g, h y las señales obtenidas g 0 , h0 en
un gráfico para cada señal.
6) Calcular el porcentaje de la varianza que se ha perdido en cada trasformación para cada señal (la varianza de la diferencia h0 − h dividida por la
varianza de h, idem g).
7) Dar explicación de los resultados:
Solucion
Dado el volumen de calculos utilizamos programas. La entrada – solo una
linea. FT, transformacion directa de 8 puntos reales:
# ft.awk
BEGIN{
pi2=2*3.1415926; }
{
for(j=0;j<8;j++) {
2
s=0; c=0;
for(k=0;k<8;k++) {
c+=$(k+1)*cos(pi2*k*j/8);
s+=$(k+1)*sin(pi2*k*j/8);
}
printf "%f %f ",c/sqrt(8),s/sqrt(8);
}
print "";
}
La parte real de la FT inversa:
# ift.awk
BEGIN{ pi2=2*3.1415926; }
{
for(j=0;j<8;j++) {
c=0;
for(k=0;k<8;k++)
c+=$(2*k+1)*cos(pi2*k*j/8)+$(2*k+2)*sin(pi2*k*j/8);
printf "%f\n",c/sqrt(8);
}
}
DCT – directa:
# dct.awk
BEGIN{ pi=3.1415926;}
{
s=0;
for(i=1;i<=8;i++) s+=$i;
s/=2;
printf "%f ",s;
for(k=1;k<8;k++) {
s=0;
for(j=0;j<8;j++)
s+=$(j+1)*cos(pi*k*(j+1/2)/8);
printf "%f ",s;
}
print "";
}
DCT – inversa.
3
# idct.awk
BEGIN{ pi=3.1415926;
}{
for(j=0;j<8;j++) {
s=0;
for(k=0;k<8;k++)
s+=$(k+1)*cos(pi*k*(j+1/2)/8);
printf "%f\n",s*2/8;
}
}
Para la estimacion de la varianza podemos utilizar una hoja de calculo o el
siguinte script:
{ k++; n[k]=$1;} # guerdamos los datos en un array -- los 2 sets concatenados.
END{
# Al final del fichero.
m=k/2;
# m -- numero de muestras en un set
for(i=0;i<m;i++) { # caculando la varianza de la diferencia.
a=n[i+1]-n[i+m+1];
s0++; s1+=a; s2+=a*a;
}
print "ave=",s1/s0,"var=",(s2-s1/s0*s1)/(s0-1);
}
Utilizando los escripts podemos hacer los calculos. Por ejemplo, las
siguientes lineas
echo "3 5 5 3 3 1 1 3" | awk -f dct.awk|tee s1.dct| awk -f idct.awk > s1.data
hacen la transformada directa y inversa DCT y guardan los resultados en
s1.*. Los detalles para la senal 3,3,4,1,0,-1,-2,-7 estan en el apendice B.
Los resultados son:
4
SENAL:
3 3 4 1 0 -1 -2 -7
Fourier
|
DCT
---------------------------------------| RE
| IM
----------------------------------F_0
| 0.35 | DCT_0 | 0.50
F_1
| 0.06 | 5.12
DCT_1 | 16.94
F_2
| 0.35*| 2.83
DCT_2 | -5.38
F_3
| 2.06*| 0.88*
DCT_3 | 1.88
F_4
| 3.18*| DCT_4 | -4.95*
F_5
| 2.06*| -0.88*
DCT_5 | 2.46*
F_6
| 0.35*| -2.83
DCT_6 | -0.07*
F_7
| 0.06 | -5.12
DCT_7 | 2.35*
----------------------------------* Componentes que anulamos
Hay que conservar solo 4 componentes independientes
con mas bajas frecuencias =>
las inversas se hacen con las siguientes coecientes
(tabla izquierda).
| RE
| IM
D C T
SENAL |
FT’ | DCT’
---------------------------------------------------------F_0
| 0.35 | DCT_0 | 0.50
3
| 0.17 | 3.43
F_1
| 0.06 | 5.12
DCT_1 | 16.94
3
| 4.72 | 3.04
F_2
| 0
| 2.83
DCT_2 | -5.38
4
| 3.75 | 2.53
F_3
| 0
| 0
DCT_3 | 1.88
1
| 0.66 | 1.93
F_4
| 0
| DCT_4 | 0
0
| 0.08 | 0.80
F_5
| 0
| 0
DCT_5 | 0
-1
| -0.47 | -1.25
F_6
| 0
| -2.83
DCT_6 | 0
-2
| -3.48 | -3.82
F_7
| 0.06 | -5.12
DCT_7 | 0
-7
| -4.41 | -5.66
--------------------- -----------------------------------Varianza: 12.70 | 2.92 | 1.29
| 23%
| 10%
La senal recuparada con solo 4 componentes esta representada
en la tabla derecha.
La ultima fila es la varianza de la diferencia entre la senal
original la recuperada. DCT es mucho mejor.
5
Para la segunda senal:
SENAL: 3 5 5 3 3 1 1 3
FT y DCT
Varianza del
SENAL INVERSA
# |
RE
IM |
DCT
SEN | FT’ | DCT’
---=------------------------- ----------------0 | 8.49
- | 12.00
3 | 3.71 | 3.38
1 | 1.00
2.41 | 5.55
5 | 4.71 | 4.38
2 | 0.00
0.00 | -0.00
5 | 4.71 | 4.92
3 | -1.00* -0.41* | -4.70
3 | 3.71 | 3.92
4 | 0.00*
- | -0.00*
3 | 2.29 | 2.08
5 | -1.00* 0.41* | -3.14*
1 | 1.29 | 1.08
6 | 0.00
0.00 | -0.00*
1 | 1.29 | 1.62
7 | 1.00 -2.41 | 1.10*
3 | 2.29 | 2.62
----------------Varianza:
2.29| 0.33 | 0.40
----------------14% | 17%
FT ligeramente mejor.
6
5
Signal
FT
DCT
Signal
FT
DCT
5
4
0
3
−5
2
1
−10
0
2
4
6
0
8
0
2
4
6
8
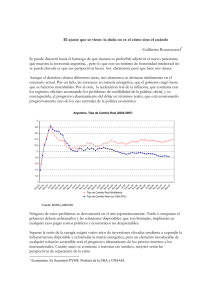
Figure 1: La representacion de las senales, las inversas con cuatro componentes
de FT y DCT. Se puede ver que para senales periodicas FT es un poco mejor que
DCT, y para senales aperiodicas DCT es mucho mejor que FT.
6
JPEG. Problema opcional. 1 punto.
Suponemos que comprimimos imágenes utilizando las técnicas de JPEG,
sustituyendo la transformada de cosenos (DCT) por la siguiente transformada:
T [g] = R.g,
donde g(t) es la señal unidimensional de 8 puntos, y






1
R= 
2






1
1
1
1
1
1
1
1
1
1
1
1 −1 −1 −1 −1 


1
1 −1 −1
0
0
0
0 

0
0
0
0
1
1 −1 −1 

1 −1
0
0
0
0
0
0 

0
0
1 −1
0
0
0
0 


0
0
0
0
1 −1
0
0 
0
0
0
0
0
0
1 −1
(wavelet de Haar)
1) Utilizando esta transformada y la imagen de Lena, construir la distribución de al menos 3 componentes de los 64.
2) Encontrar la transformada inversa de R.
3) Utilizando la siguiente matriz de cuantificación, ¿Cuál es el PSNR
comprimiendo la imagen de Lena de la tercera práctica?







R=






1
1
1
1
200
200
200
200
1
1
1
1
200
200
200
200
1
1
1
1
200
200
200
200
1
1
1
1
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200
200














PSNR=.......
Solucion
Subproblema:
1) Elegimos los componentes 0,0, 0,1, y 1,1. Los resultados estan en los
graficos para los componentes 0,0; 0,1 y 1,1. Se puede ver que salvo 0,0 todos
los elementos tienen distribución parecida. Notar la escala semi-logaritmica
de las distribuciones.
7
2) Cada fila es ortagonal a cada otra. Por eso R.R T es diagonal. Multiplicamos R por RT y tenemos:
V = R.RT = diag(2, 2, 1, 1, 1/2, 1/2, 1/2, 1/2)
No existen elementos nulos y por tanto la matriz inversa de R existe y es:







−1 T
−1
(R ) = V .R = 







1/4 1/4
1/4
1/4
1/4
1/4
1/4
1/4
1/4 1/4
1/4
1/4 −1/4 −1/4 −1/4 −1/4 


1/2 1/2 −1/2 −1/4
0
0
0
0 

0
0
0
0
1/2
1/2 −1/2 −1/2 

1 −1
0
0
0
0
0
0 

0
0
1
−1
0
0
0
0 


0
0
0
0
1
−1
0
0 
0
0
0
0
0
0
1
−1
3) El valor de los ultimos componentes (con paso de cuantizacion 200)
no sobrepasa 128. Por tanto solo nos quedamos con los primeros 4x4 componentes, lo que es equivalente de bajar la resolucion de la imagen 2 veces.
Por tanto MSE coincide con el D0 = 46 de la segunda practica y PSNR es:
P SN R = 10 log10
8
2552
= 31.5[dB]
46
Apendice A
Compresion LZ:
# ejecutar con awk -f lz.awk
# entrada-ejemplo aaaabbccaaaabbccaaaabbcc
#
BEGIN{
del=sprintf("%c",39);
}{
a=$0; l=length(a); # cadena de compirmir -- la linea de entrada
for(i=1;i<=l;) {
imax=i; lmax=0; # la longuitud y la posicion maxima encontrada por defecto
for(;;) {
ic=index(a,substr(a,i,lmax+1)); # buscamos nueva long. maxima.
if (ic>=i) break;
# no hay ==> codificar.
imax=ic;
# establecer nueva posicion
j=imax+lmax+1; k=i+lmax+1;
# determinar su longuitud
while(k<=l && substr(a,j,1)==substr(a,k,1)) { j++; k++; }
lmax=j-imax;
if(k>l) break; #si hemos llegado al final de la cadena -- salir.
}
if (i+lmax>l) pr="EOF";
else
pr= del substr(a,i+lmax,1) del;
printf "%4d %4d %s \n",lmax,i-imax,pr;
#
print substr(a,1,imax-1) ">" substr(a,imax,i-imax) \
# "[" substr(a,i,lmax+1) "]" substr(a,i+lmax+1);
i+=lmax+1;
}
}
Apendice B
Calculos detallados problema 2.
# Calcular la directa y la inversa -- tiene que coincidir con la sennal
>echo "3 3 4 1 0 -1 -2 -7" | awk -f dct.awk | awk -f idct.awk > s0.data
9
# Calcular la dct directa:
> echo "3 3 4 1 0 -1 -2 -7" | awk -f dct.awk | tee s0.dct8
0.500000 16.938142 -5.384764 1.879747 -4.949746 2.458696 -0.065656 2.349613
# Copiamos los cuatro componentes con mas bajas frecuencias (con el raton)
#
y calculamos la inversa:
> echo "0.500000 16.938142 -5.384764 1.879747 0 0 0 0" | \
? awk -f idct.awk > s0.dct4
# Aplicamos la transformada de Fourier:
> echo "3 3 4 1 0 -1 -2 -7" | awk -f ft.awk | tee s0.ft8
0.353553 0.000000 0.060660 5.121320 0.353554 2.828427 \
2.060660 0.878679 3.181981 -0.000001 2.060660 -0.878680 \
0.353552 -2.828427 0.060658 -5.121319
#
# 1) Elegimos solo los 4 coecientes independentes,
#
correspondintes a las frecuencias mas bajas
# f_0
-- tiene solo parte real.
# f_1 y f_7 -- Re[f_1]=Re[f_7] y Im[f_1]=-Im[f_7]
# una de las Re[f_2] o Im[f_2] -- elego la imaginaria porque es mas frande:
# f_2 -- Im[f_2]=-Im[f_6]
# anulo todos los componentes restante y hago la transformada inversa:
# (por favor concatenar las lineas)
#
>echo "0.353553 0.000000 0.060660 5.121320 0 2.828427 \
0 0 0 0 0 0 0 -2.828427 0.060658 -5.121319" | \
? awk -f ift.awk | tee s0.ft4
0.167892
4.715989
3.746319
0.655330
0.082107
-0.465990
-3.496320
-4.405330
# hago un fichero (zero) que contiene 8 lineas con 0.
# calculo las varianzas.
10
>cat s0.data zero | awk -f var.awk
ave= 0.125 var= 12.6964
>cat s0.data s0.ft4 | awk -f var.awk
ave= 6.25e-07 var= 2.91597
>cat s0.data s0.dct4 | awk -f var.awk
ave= 2.5e-07 var= 1.28822
# hago un grafico utilizando una hoja de calculo o parecido.
# segun el programa imprimo el resultado
xmgr s0.data s0.ft4 s0.dct4 &
11
8
1e−01
1e−02
Probabilidad
Probabilidad %
6
4
1e−03
2
1e−04
0
0
1000
2000
3000
Valor componente 0,0
0
1000
4000
2000
3000
Valor componente 0,0
4000
Figure 2: Componente 0,0.
80
1e+00
1e−01
Probabilidad
Probabilidad %
60
40
1e−03
20
0
−1000
1e−02
0
Valor componente 1,0
1e−04
−1500
1000
−500
500
Valor componente 1,0
1500
Figure 3: Componente 1,0.
80
1e+00
1e−01
Probabilidad
Probabilidad %
60
40
1e−03
20
0
−1000
1e−02
0
Valor componente 1,1
1e−04
−600
1000
−400
Figure 4: Componente 1,1.
12
−200
0
200
Valor componente 1,1
400
600