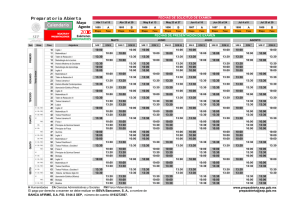
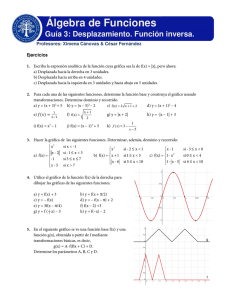
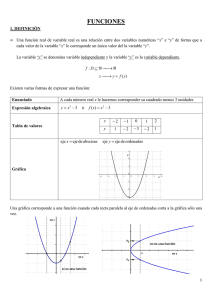
Factores: x3 – 4x = x(x2 – 4) = x(x + 2)(x – 2) Raíces:

2009 – II
Facultad de Contabilidad y Finanzas
SOLUCIONARIO DE LA PRÁCTICA CALIFICADA Nº 2 - A
Curso
:
ANÁLISIS MATEMÁTICO I
Turno
:
Mañana
Docente
Ciclo
:
:
Ing. Oscar Reyes Almora
V
Sección
:
Extraordinaria
3
1. Bosqueje la gráfica de la siguiente función f(x) = x – 4x.
Factores: x3 – 4x = x(x2 – 4) = x(x + 2)(x – 2)
Región
]-∞, -2[
]-2, 0[
]0, 2[
]2, ∞[
Valor de prueba
-3
-1
1
3
(3 puntos)
Raíces: -2, 0, 2
f(x)
-15
3
-3
15
Ubicación
Debajo del eje x
Encima del eje x
Debajo del eje x
Encima del eje x
2. Marque con un aspa indicando el tipo de función correcta.
(3 puntos)
Par
Impar
(X)
(
)
Ninguna
(
)
¿por qué?
Porque es simétrica con respecto al
eje y
Par
Impar
(
(
)
)
Ninguna
(X)
¿por qué?
Porque no es simétrica con respecto
al eje y, ni simétrica con relación al
origen.
Par
Impar
(
(X)
)
Ninguna
(
)
¿por qué?
Porque es simétrica con relación al
origen.
3. Aplique la teoría de traslaciones y reflexiones a la siguiente función para representarla
gráficamente. Posteriormente determine el dominio e imagen.
(3 puntos)
______
g(x) = √ x + 1 – 3
Función base:
f(x) = √ x
Traslación horizontal hacia la izquierda:
Traslación vertical hacia abajo:
___
f(x+1) = √ x+1
___
g(x) = √ x+1 – 3
f(x+1)
f(x)
g(x)
Dom (g) = [ -1, ∞ [
Img (g) = [ -3, ∞ [
4. Bosqueje la gráfica de cada función, indicando las asíntotas verticales y horizontales.
Posteriormente determine el dominio e imagen de cada una.
a) h(x) = 2x + 3
(2 puntos)
x+2
Asíntota vertical:
x = -2
Dom (h) = R – {-2}
Asíntota horizontal: y = 2
Img (h) = R – {2}
b) k(x) = - x .
(2 puntos)
x–2
Asíntota vertical:
Dom (k) = R – {2}
x=2
Asíntota horizontal: y = -1
Img (k) = R – {-1}
5. Determine, si existe, las coordenadas del punto de intersección de las gráficas de las
siguientes funciones:
y = -x+ 6
y = x2 – 1
(2 puntos)
En el punto de intersección se cumple:
-x+ 6 = x2 – 1 → x2 – 1 + x – 6 = 0 → x2 + x – 7 = 0
Aplicando la fórmula general:
x1 = [-1 + √ (12 – 4(1)(-7))]/2(1) = [-1 + √ (1 + 28)]/2 = (-1 + √ 29)/2 ≈ 2,19
x2 = (-1 – √ 29)/2 ≈ -3,19
y1 = (1 – √ 29)/2 + 6 ≈ 3,81
y2 = (1 + √ 29)/2 + 6 ≈ 9,19
∴ ((-1 + √ 29)/2, (13 – √ 29)/2 y ((-1 – √ 29)/2, (13 + √ 29)/2
6. Considerando la siguiente gráfica:
F
G
Se pide:
a. Determine el dominio e imagen de las funciones F y G.
Dom (F) = [-2, 3]
Img (F) = [1, 5]
Dom (G) = [-1, 4]
Img (G) = [-1, 3]
b. Defina las funciones F y G.
1,
F(x) =
(2 puntos)
si -2 ≤ x ≤ -1
x + 2, si -1 < x ≤ 3
3,
G(x) =
(1 punto)
si -1 ≤ x ≤ 0
-x + 3, si 0 < x ≤ 4
c. Represente gráficamente y defina la función F + G.
(2 puntos)
Dom (F+G) = Dom(F) ∩ Dom(G) = [-1, 3]
-1 ≤ x ≤ 0 :
(F+G)(x) = F(x) + G(x) = x + 2 + 3 = x + 5
0<x≤3:
(F+G)(x) = F(x) + G(x) = x + 2 + -x + 3 = 5
x + 5,
si -1 ≤ x ≤ 0
5,
si 0 < x ≤ 3
(F+G)(x) =
EL PROFESOR