Práctica Ordenador 4 Feedback

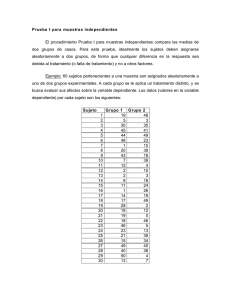
 Diseños de Investigación
4ª PRÁCTICA DE ORDENADOR (FEEDBACK)
Una empresa de automóviles desea probar la eficacia de un nuevo programa de
incentivos destinado a incrementar el ritmo de producción de sus operarios. A tal fin,
se seleccionan dos secciones de montaje de dos factorías distintas de dicha empresa:
una seguirá su ritmo habitual de trabajo (grupo control), mientras que en la otra se
implementará un programa de incentivos (grupo experimental). Se tomarán medidas
de ambos grupos antes y después de aplicar el tratamiento —programa de
incentivos—. La variable dependiente será el número de piezas montadas en una
hora. A continuación presentamos la tabla con los datos obtenidos.
Grupo control
pretest
2
2
3
3
4
4
7
5
1
2
Grupo experimental
pretest
postest
12
8
14
9
13
9
14
10
9
4
10
6
12
7
13
7
13
7
11
8
postest
6
6
5
7
5
7
9
9
3
4
EJERCICIOS
1. ¿Se cumple la condición de aplicación del ANOVA de datos de diferencia?
Interprete su respuesta.
Prueba de igualdad de Levene de varianzas de
errora
Variable dependiente: diferencia
F
df1
df2
Sig.
1,000
1
18
,331
Prueba la hipótesis nula que la varianza de error
de la variable dependiente es igual entre grupos.
a. Diseño : Interceptación + Tratamiento
La hipótesis nula establece la igualdad de las variancias poblacionales. Como p = 0,331 no se rechaza la hipótesis nula y podemos concluir que se cumple la condición de homogeneidad de variancias.
Diseños de Investigación
2. A partir de los resultados del ANOVA de datos de diferencia ¿se puede concluir
que el sistema de incentivos es eficaz para incrementar el ritmo de trabajo de los
operarios? Interprete su respuesta.
Pruebas de los efectos inter-sujetos
Variable dependiente:diferencia
Suma de
Origen
cuadrados tipo III
gl
Media cuadrática
F
Sig.
Modelo corregido
16,200a
1
16,200
14,580
,001
Intersección
273,800
1
273,800
246,420
,000
Tratamiento
16,200
1
16,200
14,580
,001
Error
20,000
18
1,111
Total
310,000
20
36,200
19
Total corregida
a. R cuadrado = ,448 (R cuadrado corregida = ,417)
La hipótesis nula establece la igualdad de las medias de las puntuaciones de diferencia (o de las puntuaciones de cambio) en ambos grupos. Como p = 0,001 se rechaza la hipótesis nula. En conclusión, hay diferencias entre las medias de las puntuaciones de cambio de los grupos. Estadísticos descriptivos Variable dependiente: diferencia Tratamiento Media Desviación típica N control 2,80
1,135
10
experimental 4,60
,966
10
Total 3,70
1,380
20
El grupo experimental tiene una puntuación de cambio mayor que el grupo control, por lo que concluimos que el incremento en la producción es mayor en el primer grupo. En conclusión, los resultados demuestran que el nuevo programa de incentivos es eficaz. 3. ¿Se cumple la condición de homogeneidad de las pendientes de regresión para
poder utilizar el ANCOVA? Interprete su respuesta.
Diseños de Investigación
Pruebas de los efectos inter‐sujetos Variable dependiente: postest Suma de cuadrados tipo III Origen Media cuadrática gl F Sig. 220,948a
3
73,649
62,509 ,000
Intersección 30,535
1
30,535
25,916 ,000
Tratamiento 3,175
1
3,175
2,694 ,120
40,625
1
40,625
34,480 ,000
,145
1
,145
,123 ,730
Error 18,852
16
1,178
Total 1896,000
20
239,800
19
Modelo corregido pretest Tratamiento * pretest Total corregida a. R cuadrado = ,921 (R cuadrado corregida = ,907) El cumplimiento de esta condición implica que las pendientes de las rectas de regresión sean homogéneas. La interacción Tratamiento x Pretest no es significativa (p = 0,73), por lo que concluimos que las pendientes de regresión son homogéneas. 4. A partir de los resultados del ANCOVA ¿se puede concluir que el sistema de
incentivos es eficaz para incrementar el ritmo de trabajo de los operarios?
Interprete su respuesta.
Pruebas de los efectos inter‐sujetos Variable dependiente: postest Origen Suma de cuadrados tipo III Media cuadrática gl F Sig. 220,803a
2
110,401
98,795 ,000 Intersección 33,629
1
33,629
30,094 ,000 pretest 40,803
1
40,803
36,514 ,000 Tratamiento 10,731
1
10,731
9,603 ,007 Error 18,997
17
1,117
Total 1896,000
20
239,800
19
Modelo corregido Total corregida a. R cuadrado = ,921 (R cuadrado corregida = ,911) Diseños de Investigación
Medias marginales estimadas
Tratamiento
Variable dependiente: Postest
Intervalo de confianza al 95%
Tratamiento
Control
Experimental
Media
Error estándar
Límite inferior
Límite superior
7,915a
,449
6,967
8,864
10,285a
,449
9,336
11,233
a. Las covariables que aparecen en el modelo se evalúan en los valores siguientes: Pretest
= 5,4000.
El efecto del Tratamiento es estadísticamente significativo (p = 0,007). Mirando las medias estimadas vemos que el grupo experimental produce una media mayor de piezas (10,285) que el grupo control (7,915). En conclusión, el sistema de incentivos es eficaz para incrementar el ritmo de trabajo de los operarios.