Taller

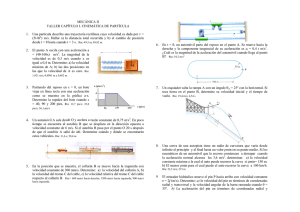
TEMA 1. MOVIMIENTO RECTILINEO
1. La posición de una partícula que describe una línea recta queda definida mediante la
expresión s = t3/3 − 9t + 2, donde si t está en s, s resulta en m. Determine: a) la aceleración
de la partícula cuando su velocidad es de 7 m/s; b) su velocidad media desde t = 3 hasta t =
6 s. c) Dibuje las gráficas tiempo-posición, tiempo-velocidad y tiempo-aceleración del
movimiento de la partícula, durante los primeros seis segundos.
Rta: 8 m/s2; 6,66 m/s.
2. La velocidad de un punto P que se mueve sobre el eje de las ordenadas, que es un eje
vertical dirigido hacia arriba, se puede expresar como v = 6 t2 − 24, en donde v se da en
pie/s y t en s; además, cuando t = 0, entonces y = 6 pie. Calcule: a) la magnitud y la
dirección de la aceleración del punto cuando t = 3 s; b) el desplazamiento del punto P
durante los primeros cuatro segundos; c) la longitud que recorre durante ese mismo lapso.
d) Dibuje esquemáticamente las gráficas del movimiento del punto P.
Rta: 36 pie/s2; 32 pie; 44 pie
3. La magnitud de la aceleración de un collarín que se desliza sobre una barra horizontal se
expresa, en función de su posición, como a =12, donde a se da en pul/s2 y x en pul. Cuando
t = 2 s, entonces v = 32 pul/s y x = 16 pul. Determine la posición, la velocidad y la
aceleración del collarín cuando t = 3s.
Rta: 54 pulg, 44 pulg/s; 12 pul/s2
4. Un ascensor sube con velocidad constante de 2 m/s. Cuando se encuentra a 10 m sobre el
nivel del suelo los cables se rompen. Prescindiendo del rozamiento, Calcular la máxima
altura a que llega la cabina, Si los frenos de seguridad actúan automáticamente cuando la
velocidad del descenso alcanza el valor de 4 m/s, determinar la altura en la que actúan los
frenos.
Rta: 10,2 m; 9,38 m.
5. El punto A oscila con una aceleración a = (40-160x) m/s2. La magnitud de la velocidad es
de 0,3 m/s cuando x es igual a 0,4 m. Determine: a) la velocidad máxima de A; b) las dos
posiciones en las que la velocidad de A es cero.
Rta: 1,921 m/s, 0,0981 m y 0,402 m.
6
Una partícula se proyecta hacia la derecha desde la posición x=0 con una velocidad inicial
de 9 m/s. Si la aceleración de la partícula se define como a= -0,6 v3/2 donde a y v se
expresan en m/s2y m7s, determine, la distancia que ha recorrido la partícula cuando su
velocidad sea 4 m/s y el tiempo cuando v=1 m/s. Determinar también el tiempo cuando
haya recorrido 6 m.
Rta: 3,33 m; 2,22 s; 1,667 s.
7
Un automóvil viaja a una velocidad constate de 54 km/h cuando su conductor ve a una niño
sobre el camino. El conductor aplica los frenos hasta que el niño regresa a la acera y
después acelera para recuperar su velocidad original. En la figura se presenta el registro de
la aceleración del automóvil. Se supone que en x=0 cuando t=0. Determine a) el tiempo t1
en el que la velocidad vuelve a ser de 54 km/h, b) la posición del automóvil en ese
momento, c) la velocidad promedio del automóvil.
Rta 18 s; 178,8 m; 34,7 km/h
8
Un tren que viaja a 50 mi/h se encuentra a 3 mi de una estación. El tren desacelera de modo
que su velocidad es de 20 mi/h cuando se encuentra a 0,8 mi de la estación. Si el tren llega
a la estación 7,5 minutos después de que empieza a desacelerar y suponiendo
desaceleraciones constantes, determine a)El tiempo que requiere para recorrer las primeras
2,2 mi b)la velocidad del tren en la estación, c) la aceleración constante final del tren.
Rta: 226 s; 5,7 mil/h; 230 mi/h2.
9
Un motociclista arranca del punto A con una aceleración constante a1 = 2,4 pie/s2 hacia la
derecha. Cuatro segundos después, un automóvil pasa por el punto B, situado a 200 pie de
A, viajando hacia la izquierda. Sabiendo que la velocidad del automóvil es v2 = 30 pie/s y
constante, diga en dónde el motociclista encuentra el automóvil. Desprecie el tamaño de los
vehículos.
Rta: 78 pies a la derecha de A.
10 Partiendo del reposo en s = 0, un bote viaja en línea recta con una aceleración como se
muestra en la gráfica a-s. Determine la rapidez del bote cuando s = 40, 90 y 200 pies.
Rta: 12,64 pie/s; 22,8 pie/s y 114 pie/s
11 Si el cable A se mueve hacia abajo con una velocidad de 2 m/s, determine la velocidad del
bloque E.
Rta: 0,25 m/s hacia arriba.
12 En la posición que se muestra, el collarín B se mueve hacia la izquierda con velocidad
constante de 300 mm/s. Determine: a) la velocidad del collarín A, b) la velocidad del
tramo C del cable, c) la velocidad relativa del tramo C del cable respecto al collarín B.
Rta:= 600 mm/s hacia derecha; 1200 mm/s hacia izquierda; 900 mm/s hacia izquierda.