UNIDAD 6. La Hipérbola La Hipérbola

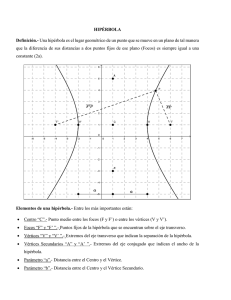
UNIDAD 6.
La Hipérbola
La Hipérbola
Juan Adolfo Álvarez Martínez
Autor
UNIDAD 6
Definición
Se conoce como hipérbola al lugar geométrico de los puntos del plano
tales que la diferencia de sus distancias a dos puntos fijos, llamados
focos, es una constante.
La distancia entre dos vértices de la hipérbola se llama eje transverso
(eje real de la hipérbola), y el segmento perpendicular en el punto medio
del eje transverso o real se llama eje conjugado (eje imaginario).
El punto donde se cortan ambos ejes (que es, evidentemente, el punto
medio de los focos) se llama centro de la hipérbola.
La longitud del eje transverso (distancia entre los dos vértices) se
identifica como: 2a
La longitud del eje conjugado mediante: 2b
La distancia entre los focos: 2c
Los puntos donde la hipérbola corta a los ejes (se verá que únicamente
corta al eje real) se llaman vértices de la hipérbola.
Al igual que en la elipse, se llama distancia focal a la distancia entre los
dos focos.
A diferencia de la elipse, aquí se tiene 2c > 2a (por tanto c > a) y se
puede considerar que:
.
Este valor se llama semieje imaginario (o conjugado) de la hipérbola.
En cada hipérbola, los parámetros a, b, c están relacionados por:
b2= c2-a2
Hipérbola.
En la siguiente figura se observa la grafica de una hipérbola con el eje
real en “x”
Al igual que en la elipse, se considerarán en primer lugar las hipérbolas
centradas en el origen de coordenadas y con focos en el eje de abscisas.
La ecuación de una hipérbola con centro en el origen y con focos sobre
el eje “x” es:
Cuando
la hipérbola tenga
el eje real sobre “y”, la ecuación es:
Y la grafica se muestra a continuación.
Ejemplo 1.
Obtener la ecuación de la hipérbola que tiene por vértices los puntos (3,0) y
(-3,0), así como sus focos son los puntos cuyas coordenadas son F1(5,0) y
F2(-5,0).
Solución:
Con los datos indicados y tomando en cuenta que es preciso localizar los
puntos de los focos en el plano, observamos que están sobre “x”, además de
que el punto medio de estos es el origen, inmediatamente deducimos que la
ecuación es de la forma:
Y de los datos vemos que la distancia entre los vértices Es 2a = 6, significa
que la longitud del eje real es entonces a = 3 , y también como la distancia
entre los focos es 2c = 10, se obtiene que c = 5.
Con esta información calculamos el valor de b mediante:
b2= c2-a2 , de donde :
=
y ahora podemos sustituir en la ecuación conocida
De donde resulta: a2=9,
b2= 16
Quedando la ecuación ordinaria como:
Luego el valor de la excentricidad es:
Y la grafica de la hipérbola se observa a continuación.
Ejemplo 2.
Calcular los elementos de la hipérbola cuya ecuación es: 9x2 –4y2 –36=0
Solución. Ahora procederemos primero a la operación inversa; tenemos la
ecuación general y se trata de obtener la ecuación ordinaria para que en base
a ella se determinen los valores de la distancia entre vértices (a), la distancia
entre focos (c).
Para lograrlo, vamos a realizar una división entre 36 y pasamos el término
independiente a la derecha para poder tener la ecuación en una de las formas
conocidas. Esto es:
Y comparamos con las ecuaciones conocidas, notando es similar a:
Que como vemos es una hipérbola que tiene sus focos sobre “x”, y de esta
ecuación sabemos que a2 = 4,
b2 = 9, por lo que entonces a=2 y la
distancia entre los vértices es 2a=4, con lo que los vértices tienen coordenadas
(2,0) y (-2,0)
Asimismo como b2 = 9 entonces b= 3 y la longitud del eje conjugado es 2b=6
Con estos valores de “a”, “b” podemos calcular “c” que nos será de utilidad en
el cálculo de las coordenadas de los focos.
El valor de c se obtiene mediante b2= c2-a2 , despejamos c: resultando:
C2= b2+a2, sacamos raíz cuadrada:
Por lo que los focos son entonces: F1(3.6 ,0) y F2(- 3.6 , 0)
La excentricidad es:
El lado recto de la hipérbola se calcula mediante:
La grafica de la parábola se muestra a continuación
HIPERBOLA CON CENTRO FUERA DEL ORIGEN
Y EJE REAL (TRANSVERSO) PARALELO AL EJE “X”
Ecuación ordinaria:
( x – h) 2
a2
–
(y – k)2
b2

1
Donde (h,k) son las coordenadas del Centro de la hipérbola
HIPERBOLA CON CENTRO FUERA DEL ORIGEN
Y EJE REAL (TRANSVERSO) PARALELO AL EJE “Y”
Ecuación ordinaria:
(y – k)2
a2
–
( x – h) 2
b2

1
Donde (h,k) son las coordenadas del Centro de la hipérbola
Vamos a resolver un ejemplo donde apliquemos la formula y observemos el
procedimiento.
Ejemplo 3.
Determine la ecuación ordinaria y general de la hipérbola cuya grafica se muestra a
continuación.
Primero vamos a identificar las coordenadas del centro de la hipérbola. Vemos de
manera inmediata que es el punto A (h,k)= (3,-1), luego los vértices (3,1) y (3,-3).
Los focos son los puntos cuyas coordenadas son: (3,2) y (3,-4).
Esta información nos es de utilidad ya que la distancia del centro a los vértices es:
a=2 y la distancia del centro a los focos es: c=3.
De manera que si ocupamos la formula:
c2= b2+a2 y despejamos “b” queda:
Ahora procedemos a usar la ecuación que corresponde a la hipérbola con centro fuera
del origen y eje real paralelo a “y” que es:
Que sustituyendo los valores indicados anteriormente:
(h,k)= 3,-1
a= 2,
Tenemos: