Una aerolınea mantiene vuelos regulares entre 4 ciudades, en
Anuncio

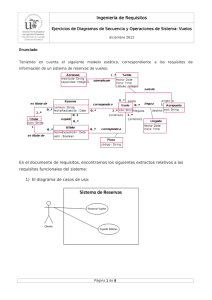
Una aerolı́nea mantiene vuelos regulares entre 4 ciudades, en todos los casos con vuelos de ida y vuelta. En la siguiente tabla se dan, en la primera parte las distancias entre cada par de ciudades; en la segunda, las demandas de vuelos para un dı́a dado, y en la tercera, las plazas aún disponibles. Distancias C1 C1 0 C2 C3 2450 2610 Demandas Disponibles C4 C1 C2 C3 C4 C1 C2 C3 C4 340 - 15 8 5 - 32 15 7 C2 2450 0 160 2560 20 - 7 12 10 - 20 15 C3 2610 160 0 2700 8 40 - 9 28 25 - 12 C4 2560 2700 0 10 19 3 - 20 22 8 - 340 Se trata de encontrar la programación de los vuelos que cubriendo la demanda de los mismos, genere los menores desplazamientos. 1 La solución óptima com AMPL produce la siguiente salida: CPLEX 10.1.0: optimal solution; objective 329380 16 dual simplex iterations (0 in phase I) coste_total = 329380 x := p1 c1 c2 15 p1 c1 c3 8 p1 c1 c4 5 p2 c2 c1 10 p2 c2 c3 14 p2 c2 c4 15 p2 c3 c1 7 p2 c4 c1 3 p3 c1 c2 13 p3 c3 c1 21 p3 c3 c2 25 p3 c3 c4 11 p3 c4 c2 2 p4 c4 c1 10 p4 c4 c2 19 p4 c4 c3 3 2