unidad - eCasals
Anuncio

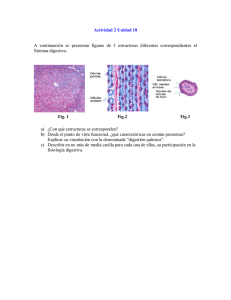
3 UNIDAD Transformaciones geométricas CONOCIMIENTOS TEÓRICOS 1 Concepto y tipos de transformaciones 1.1 Transformaciones isométricas 1.2 Transformaciones isomórficas 2 Homología 2.1 Homología en el espacio 2.2 Homología en el plano. Características 2.3 Rectas límite de una homología plana 2.4 Construcciones fundamentales en homología plana 2.5 Determinación de una homología plana 3 Afinidad 4 Inversión 4.1 4.2 4.3 4.4 Concepto de inversión y elementos Inverso de un punto Inversa de una recta Inversa de una circunferencia APLICACIONES PRÁCTICAS 1 Utilización de las transformaciones 1.1 Aplicación de la homotecia 1.2 Aplicaciones de la homología 1.3 Aplicaciones de la afinidad 1.4 Resolución de tangencias por inversión CUESTIONES Y EJERCICIOS UNIDAD 3 CONOCIMIENTOS TEÓRICOS Transformaciones geométricas Las transformaciones geométricas están íntimamente ligadas con el dibujo técnico y con la resolución de problemas, como veremos en las Aplicaciones prácticas de la presente unidad. Aplicar la transformación adecuada a los datos de un problema los convierte en otros a partir de los cuales la resolución del problema resulte más sencilla; a la solución encontrada aplicaremos la transformación inversa de la inicial para tener resuelto el problema. 1 CONCEPTO Y TIPOS DE TRANSFORMACIONES Una transformación geométrica es una operación, o la combinación de varias de ellas, que permite deducir una nueva forma geométrica a partir de otra inicial. A cada punto de la forma origen le corresponde otro de la forma transformada, al que llamaremos homólogo o imagen del primero. La figura transformada, homóloga de la original, está formada por puntos y rectas homólogos. Cuando en una transformación el elemento original y su homólogo coinciden, a éste lo llamamos elemento doble. El aspecto de la forma homóloga respecto a la original permite establecer los siguientes tipos de transformaciones: • Isométricas. El elemento homólogo conserva las dimensiones y ángulos de la forma inicial. Son las simetrías axial y central, el giro o rotación y la traslación. A todas estas transformaciones también se las denomina movimientos. • Isomórficas. El elemento homólogo conserva únicamente la forma (ángulos) de la inicial, existiendo proporcionalidad entre sus dimensiones. A este grupo pertenecen la homotecia y la semejanza. • Anamórficas. Cuando hay un cambio de forma entre la figura inicial y su homóloga. Son transformaciones de este tipo la homología, la afinidad y la inversión. Una transformación se denomina biunívoca cuando a cada elemento de la forma inicial le corresponde uno y sólo uno de la transformada, y a cada uno de los puntos de ésta, uno y sólo uno de la forma inicial. Ejemplo de diversas transformaciones geométricas en la naturaleza. 50 A las transformaciones de los dos primeros grupos anteriores, estudiadas en las unidades 7 y 8 de Dibujo técnico 1, nos referiremos brevemente en los próximos apartados, centrando esta unidad en las transformaciones anamórficas. Transformaciones geométricas TEÓRICOS UNIDAD CONOCIMIENTOS UNIDAD CONOCIMIENTOS TEÓRICOS 1.1 Transformaciones isométricas De cada una de las transformaciones de este grupo, recordaremos los elementos característicos que las definen y los elementos dobles. • Simetría axial. El elemento característico de esta transformación es el eje e de simetría (Fig. 1). Son elementos dobles el propio eje de simetría, las rectas perpendiculares a él y las circunferencias cuyo centro se halle en el eje de simetría; los puntos que forman estas circunferencias no son dobles. • Simetría central. El centro de simetría O es su elemento característico (Fig. 2). Son elementos dobles el centro de simetría, las rectas que pasan por él y las circunferencias que tengan su centro en el de simetría, aunque no estén formadas por puntos dobles. • Giro o rotación. Sus elementos característicos son el centro O y el ángulo α de giro (Fig. 3). En esta transformación, los elementos dobles son el centro de giro y las circunferencias de centro en él, aunque éstas no estén formadas por puntos dobles. • Traslación. El elemento característico de esta transformación es el vector v que define la dirección, el sentido y la distancia de la misma (Fig. 4). Los únicos elementos dobles en una traslación son las rectas paralelas a la dirección de la traslación, aunque no estén formadas por puntos dobles. Fig. 3 Fig. 1 Fig. 2 Fig. 4 1.2 Transformaciones isomórficas Cuando dos figuras semejantes (las que tienen ángulos iguales y lados proporcionales) se hallan alineadas respecto a un punto, se dice que son homotéticas (Fig. 5). El punto O en relación al cual están alineadas es el centro de homotecia, el cual, junto con la razón de la misma, forman los elementos característicos de una homotecia. Los elementos dobles de una homotecia son su centro y las rectas que pasan por el mismo, aunque no estén formadas por puntos dobles. Fig. 5 51 3 UNIDAD 3 CONOCIMIENTOS TEÓRICOS Transformaciones geométricas La homotecia puede ser directa o positiva cuando cada punto y su homólogo se hallan en la misma semirrecta con respecto al centro de homotecia, al que llamamos de homotecia directa. La homotecia será inversa o negativa cuando el centro de homotecia, inversa en este caso, se halla en el segmento comprendido entre cada punto y su homólogo. Entre dos circunferencias se pueden establecer dos relaciones de homotecia, una directa y otra inversa (Fig. 6). Al ser los centros de ambas circunferencias homólogos entre sí, los dos centros de homotecia, directo e inverso, estarán sobre la recta de unión de los centros de las circunferencias. Fig. 6 2 HOMOLOGÍA La homología es la primera de las transformaciones anamórficas que veremos en la presente unidad. A cada uno de los puntos y rectas de una forma plana inicial le corresponden, respectivamente, un punto o una recta de su forma homóloga, cumpliendo unas determinadas condiciones que veremos en los próximos apartados. 2.1 Homología en el espacio La homología en el espacio es una transformación proyectiva cuyo centro es un punto propio V. Al cortar la radiación de vértice V mediante dos planos, el del suelo y el del dibujo en la representación de la figura 7, obtendremos sobre cada uno de ellos una sección plana, ABC y A’B’C’ respectivamente. Fig. 7 52 Transformaciones geométricas CONOCIMIENTOS TEÓRICOS UNIDAD Ambas secciones son figuras homológicas en el espacio, de acuerdo con las siguientes condiciones: • Todos los rayos que pasan por V interceptan puntos homólogos, A y A’, B y B’, etc., sobre cada uno de los planos. • Las rectas homólogas se cortan en puntos del eje de la homología. Todos los puntos del eje son puntos dobles. En la representación espacial de la figura 7, el eje de la homología es la recta de intersección entre el plano del suelo y el del dibujo. • En la homología no se conservan propiedades métricas como el paralelismo o la perpendicularidad, ni las medidas de segmentos y ángulos. 2.2 Homología en el plano. Características Relación de homología entre un objeto y su sombra. Si en la figura anterior abatimos el plano del dibujo respecto a su intersección con el plano del suelo hasta que ambos coincidan, las dos secciones planas serán coplanarias y ambas definen la homología plana de la figura 8. Ésta puede definirse como una transformación geométrica biunívoca de una figura en otra, ambas coplanarias, de forma que entre ambas se cumplan las siguientes relaciones: Fig. 8 • Cada punto y su homólogo están alineados con el centro V de la homología. • Una recta y su homóloga se cortan en un mismo punto (homólogo de sí mismo, por tanto, punto doble) situado en el eje de la homología. • Las rectas que unen cada punto con su homólogo pasando por el centro de la homología son rectas dobles, al ser homólogas de sí mismas. 53 3 UNIDAD 3 CONOCIMIENTOS TEÓRICOS Transformaciones geométricas 2.3 Rectas límite de una homología plana Rectas límite son las rectas que representan el lugar geométrico de los puntos del infinito de cada una de las dos figuras o formas relacionadas por una homología plana. Al ser siempre dos las figuras homólogas, en cada homología podremos establecer dos rectas límite. Los homólogos de los puntos del infinito del triángulo A’B’C’ (Fig. 9), definen un lugar geométrico representado por la recta límite RL correspondiente al triángulo ABC homólogo del anterior. Para encontrar esta recta límite, deberemos buscar un par de puntos homólogos correspondientes a otros tantos puntos impropios de A’B’C’. Fig. 9 Por el centro V de la homología trazamos la recta VM’∞ paralela a B’A’M’∞; ambas rectas, por ser paralelas, han de cortarse en el infinito. El punto M, determinado en la intersección de VM’∞ con la recta AB, homóloga de su paralela A’B’, es el homólogo del punto M∞ del infinito de la figura A’B’C’; por tanto, M pertenece a la recta límite de su triángulo homólogo ABC. De forma similar encontramos el punto N homólogo de N’∞ del triángulo 54 Transformaciones geométricas CONOCIMIENTOS TEÓRICOS UNIDAD A’B’C’. La recta que definen los puntos M y N es la recta límite RL del triángulo ABC, posición de los puntos homólogos de los del infinito de A’B’C’. La recta límite RL’, correspondiente a los puntos del infinito del triángulo ABC, se determina de igual forma a la descrita para encontrar los puntos M y N; así encontramos S’, homólogo del punto S∞ de ABC. Sin necesidad de encontrar un segundo punto, por S’ trazamos la recta límite paralela, como la anterior, al eje de la homología. Además de la condición de paralelismo existente entre las rectas límite y de ambas con el eje, la distancia del vértice a una de las rectas límite es la misma que la distancia existente desde el eje a la segunda recta límite, siendo ambas interiores o exteriores al conjunto de vértice y eje. 2.4 Construcciones fundamentales en homología plana En una homología definida por la posición del vértice, por el eje de la misma y por una de sus rectas límite, vamos a encontrar los elementos homólogos de algunas posiciones de rectas que pueden ayudarnos, más adelante, en la resolución de problemas de aplicación de la homología. • Homóloga de una recta r cualquiera Buscaremos los homólogos de los puntos de corte de la recta r dada con el eje y la recta límite (Fig. 10). La intersección A-A’ con el eje es un punto doble en la homología, por lo que la recta homóloga r’ pasará por esta intersección. La recta VM, siendo M la intersección de la recta r dada con RL, define la posición de los puntos del infinito de r’, por lo que ésta será paralela a la dirección que define VMM’∞ (pasando, lógicamente, por el punto doble A-A’). Fig. 10 • Homóloga de una recta paralela al eje de la homología Trazamos una recta s auxiliar que se corte con r en un punto P (Fig. 11). Esta recta auxiliar intercepta los puntos A y M sobre el eje de la homología y la recta RL, por lo que determinaremos su homóloga s’ tal como hemos hecho en el apartado anterior. Conocida s’, situamos sobre ella el homólogo P’ (con ayuda de la recta VP). Por P’, también paralela al eje, trazaremos la recta homóloga buscada, r’. Fig. 11 55 3 UNIDAD 3 CONOCIMIENTOS TEÓRICOS Transformaciones geométricas • Homólogo de un punto cualquiera El homólogo de un punto P (Fig. 11) se determina haciendo pasar por él una recta s cualquiera. Encontramos la homóloga s’ de esta recta auxiliar y sobre ella, según la correspondencia VP, encontraremos la posición del homólogo P’. 2.5 Determinación de una homología plana Hasta ahora hemos visto los diferentes elementos que cabe considerar en una homología: vértice, eje, rectas límite, puntos y rectas dobles, etc. Sin embargo, no es necesario conocer todos estos elementos para que una homología quede determinada; hay unos elementos mínimos a partir de los cuales podremos determinar los restantes de la homología. Vemos estos casos a continuación: • El vértice, el eje y el punto homólogo de uno de la figura Obtendremos los homólogos de los restantes puntos de la figura mediante la aplicación de las dos propiedades que hemos visto en 2.2 (Fig. 12). • El vértice, el eje y la recta límite de la figura dada Prolongamos uno de los lados de la figura original, el AB en la figura 13; esta recta intercepta el punto M sobre la recta límite y el punto doble 1-1’ en el eje. Por este último, trazamos la paralela a la recta VMM’∞; sobre esta paralela se hallarán A’ y B’, homólogos de A y B, determinados con las rectas VA y VB. Con las propiedades conocidas de la homología, completaremos C’. Fig. 12 56 Fig. 13 Transformaciones geométricas CONOCIMIENTOS TEÓRICOS UNIDAD • El eje, la recta límite y el punto homólogo de uno de la figura 3 En la construcción de la figura 14, prolongamos AB hasta cortar a la recta límite en el punto M y al eje en el punto doble 1-1’. Unimos este último con A’ y trazamos la paralela por M; la intersección de esta paralela con la recta AA’ nos define la posición del vértice V de la homología. Conocido este vértice, completamos, en la forma acostumbrada, los restantes vértices de la forma homóloga de la inicial. Fig. 14 • Las dos rectas límite y el vértice de homología Las rectas límite, en el caso de la figura 15, se hallan ambas entre el vértice y el eje de la homología. La posición de éste último la determinamos paralela a las rectas límite y a la misma distancia de RL’ a la que se encuentra RL de V. Conocidos estos cuatro elementos, podremos determinar la figura homóloga de cualquier otra conocida. Fig. 15 Ejemplo de homología en la naturaleza. 57 UNIDAD 3 CONOCIMIENTOS TEÓRICOS Transformaciones geométricas • Dos puntos homólogos de otros de la figura dada y la dirección del eje La unión de cada punto con su homólogo (Fig. 16) nos define dos rectas que se cortan en el vértice V de la homología. Las rectas homólogas AB y A’B’ se cortan en el punto doble 1-1’ del eje. Pasando por este punto, y paralelamente a la dirección dada del eje, trazamos éste, con lo que volveremos a tener los datos necesarios para completar el trazado de cualquier figura homóloga de otra conocida. Fig. 16 3 AFINIDAD Las formas perspectivas ABC y A’B’C’ de la figura 17 corresponden a una homología en el espacio, tal como acabamos de estudiar; en ella la intersección de los dos planos define el eje de la homología y el centro V de la radiación representa su vértice o centro. Con los mismos elementos y cuando el centro de la radiación es impropio (Fig. 18), tenemos definida una afinidad. En ambas transformaciones los Fig. 17 58 Fig. 18 Transformaciones geométricas CONOCIMIENTOS TEÓRICOS UNIDAD puntos homólogos están alineados con el centro de la radiación, sea éste propio o impropio, y las rectas homólogas se cortan en puntos dobles del eje de la transformación. 3 La afinidad, por tanto, puede considerarse como un caso particular de homología, con el centro en el infinito. Las uniones de cada punto con su homólogo definen segmentos paralelos a la dirección de afinidad (Fig. 19). Su eje es una recta de puntos dobles y carece de rectas límite. Dos formas afines en el plano pueden estar dispuestas una a cada lado del eje de la afinidad, como en el ejemplo anterior, o ambas a un mismo lado de dicho eje, como las formas triangulares de la figura 20. En ambos casos se cumplen las propiedades enunciadas de la afinidad. Fig. 19 Fig. 20 La simetría axial puede considerarse como un caso particular de afinidad; en ella la dirección de afinidad es perpendicular al eje y la razón de afinidad es -1, al estar una forma y su simétrica en semiplanos opuestos pero equidistantes del eje de la simetría. 4 INVERSIÓN La inversión es la tercera de las transformaciones anamórficas; su principal utilidad es la resolución de problemas de tangencias entre circunferencias, rectas y puntos. Si dos formas son tangentes en un punto T, sus inversas también lo serán en T’, inverso de T. La inversión conserva también los ángulos, es decir, si dos líneas se cortan en un punto P formando un ángulo, sus inversas se cortan en el punto P’, inverso de P, formando el mismo ángulo. Antes de utilizar sus aplicaciones, debemos conocer las características de esta transformación. Riley Bridget. Cuadros en movimiento, 1962. Tempera. 59 UNIDAD 3 CONOCIMIENTOS TEÓRICOS Transformaciones geométricas 4.1 Concepto de inversión y elementos Fig. 21 A partir de un punto O, llamado centro de inversión, decimos que dos puntos alineados con dicho centro, A y A’, son inversos entre sí cuando el producto de sus distancias al centro de inversión es una cantidad constante, k, llamada potencia de inversión (Fig. 21). k = OA · OA’ La potencia será positiva si ambos puntos están al mismo lado del centro de inversión, en caso contrario, será negativa. La inversión es una transformación involutiva, es decir, que si A’ es el inverso de A, éste lo será también de A’ en la misma inversión. Hay tres figuras dobles o invariantes en la inversión, es decir, que son inversas de sí mismas (Fig. 22): Fig. 22 a) Cualquier recta r que pasa por el centro de inversión O. Como el inverso de un punto A ha de estar alineado con el centro de inversión, una recta que pase por O tendrá sus inversos, lógicamente, en la propia recta. b) La circunferencia de centro en el de inversión y radio igual a la raíz cuadrada de k. Si un punto A es inverso de sí mismo se cumplirá que k = OA · OA’ = OA · OA = OA2 y, por tanto, OA será igual a la raíz cuadrada de k. A esta circunferencia se la denomina de autoinversión. c) La circunferencia que pasa, simultáneamente, por dos parejas de puntos inversos A, A’ y B, B’. Estos puntos, en aplicación del concepto de potencia que estudiaremos en la próxima unidad, han de cumplir, necesariamente, que k = OA · OA’ = OB · OB’, por lo que habrán de estar situados en la misma circunferencia. También son dobles las circunferencias, ortogonales a la de autoinversión, que pasan por pares de puntos inversos (los radios trazados a los puntos de corte entre circunferencias ortogonales son perpendiculares entre sí). 60 Transformaciones geométricas CONOCIMIENTOS TEÓRICOS UNIDAD En la figura 22c, el segmento OT, tangente a la circunferencia de puntos dobles, es la expresión gráfica de la raíz cuadrada de la potencia de inversión. En esta misma figura, las rectas que unen dos puntos no alineados con el centro de inversión, A y B, y sus inversos, A’ y B’, son antiparalelas respecto de OA y OB. En estas rectas, tal como vemos en las rectas r y s de la figura 23, se cumple que los ángulos que forman con las que unen cada punto y su inverso con el centro de inversión son iguales. Para que una inversión quede definida, debemos conocer el centro de inversión y la potencia, o el centro y un par de puntos inversos respecto a ese centro, o bien, dos pares de puntos inversos no alineados. Fig. 23 4.2 Inverso de un punto Si conocemos una pareja de puntos inversos A y A’, y queremos hallar el inverso de otro punto B respecto a la misma inversión, dibujaremos la circunferencia que pasa por A, A’ y B (Fig. 24); uniremos B con el centro de esta circunferencia y donde la recta trazada corte la circunferencia, estará B’, en aplicación de la propiedad que afirma que dos pares de puntos inversos no alineados se hallan siempre sobre la misma circunferencia. Para obtener el inverso de un punto A conocido el centro O de la inversión y la razón k de la misma, aplicaremos las propiedades de la circunferencia de puntos dobles y de las rectas antiparalelas. Dibujamos (Fig. 25), la circunferencia de autoinversión de centro O y la tangente a ella desde el punto A con tangencia en el punto doble T-T’. La perpendicular, trazada desde T-T’, al segmento AO intercepta sobre éste el punto A’ inverso de A. Las rectas AT y A’T’ son antiparalelas ya que los ángulos que forman AT con AA’O son iguales que el formado por A’T’ con TT’O. La misma figura y los mismos argumentos nos sirven cuando el punto A’, del que queremos obtener su inverso, sea interior a la circunferencia de puntos dobles: se levanta la perpendicular desde este punto a la recta A’O hasta cortar en T a la circunferencia de puntos dobles; desde T se traza la tangente a la circunferencia hasta que corte a A’O en el punto A, inverso de A’. Fig. 24 Fig. 25 61 3 UNIDAD 3 CONOCIMIENTOS TEÓRICOS Transformaciones geométricas 4.3 Inversa de una recta La figura inversa de una recta la podemos determinar en dos casos: cuando la recta pase por el centro de inversión, en cuyo caso esa recta es doble e inversa de sí misma, y cuando la recta no pase por el centro de inversión. En este segundo caso (Fig. 26), suponemos conocida la recta r de la que queremos determinar su figura inversa, el centro de la inversión O y la potencia k de la misma. Buscamos los inversos de dos puntos A y B de la recta r: del primero de ellos, intersección con r de la perpendicular trazada desde O, encontramos su inverso A’ mediante la segunda de las construcciones descritas en 4.2; conocido A’, trazamos la circunferencia que tenga por diámetro el segmento OA’. El inverso de un segundo punto cualquiera de r, punto B en la figura, tiene su inverso B’ sobre la circunferencia de diámetro OA’; en efecto, las rectas AB y A’B’ son antiparalelas respecto de OA y OB, y el ángulo OB’A’ sólo será recto si B’ se halla sobre la circunferencia de diámetro OA’. Fig. 26 El razonamiento anterior es válido para cualquier punto B de r. El inverso de una recta r que no pasa por el centro de inversión es una circunferencia r’ que sí pasa por él y que tiene por diámetro el segmento OA’. El punto A’ es el inverso de A, pie de la perpendicular a la recta r trazada desde el centro de inversión O. De forma general, dadas una circunferencia y una recta no tangentes, siempre podemos considerarlas inversas una de la otra en una inversión cuyo centro se halla en uno de los extremos del diámetro perpendicular a la recta (Fig. 27). 4.4 Inversa de una circunferencia Como acabamos de ver en 4.3, la inversa de una circunferencia que pasa por el centro de inversión es una recta que no pasa por dicho centro. Conocida la circunferencia, el centro de inversión y la razón de la misma (Fig. 28), para encontrar la figura inversa de la circunferencia, empezamos Fig. 27 62 Fig. 28 Transformaciones geométricas CONOCIMIENTOS TEÓRICOS UNIDAD por unir el centro O de inversión con el de la circunferencia, determinando sobre la misma el punto A. Por el inverso de A, A’, pasará la recta inversa perpendicularmente a la recta OA. Para encontrar A’, nos auxiliamos de los puntos diametralmente opuestos, B y B’, pertenecientes a la circunferencia de autoinversión, y trazamos una circunferencia auxiliar que pase por ellos y por A; la intersección de esta circunferencia con la recta OA define la posición de A’. Si la circunferencia no pasa por el centro de inversión (Fig. 29), su inversa será otra circunferencia que determinaremos de la siguiente manera: unimos el centro de inversión O con el centro O1 de la circunferencia, recta que determina sobre la circunferencia los puntos A y B; mediante la circunferencia de autoinversión de centro O, determinamos sus inversos A’ y B’; la circunferencia que tiene estos puntos como extremos de un diámetro es la circunferencia buscada, inversa de la inicial. Vasili Kandinsky. Sobre las puntas, 1928. Óleo sobre lienzo. Fig. 29 Terminamos el estudio de la inversión con el resumen de las principales transformaciones estudiadas: • La inversa de una recta que pasa por el centro de inversión es ella misma; recta doble. • La inversa de una recta que no pasa por el centro de inversión es una circunferencia que sí pasa por él. • La inversa de una circunferencia que pasa por el centro de inversión es una recta que no pasa por él. • La inversa de una circunferencia que no pasa por el centro de inversión es otra circunferencia que tampoco pasa por él. 63 3 UNIDAD 3 APLICACIONES PRÁCTICAS Transformaciones geométricas 1 UTILIZACIÓN DE LAS TRANSFORMACIONES En los próximos apartados veremos algunas de las aplicaciones que las transformaciones geométricas tienen en la resolución de problemas en el ámbito del dibujo técnico. 1.1 Aplicación de la homotecia Dos circunferencias son siempre figuras homotéticas en relación a una homotecia que tiene por centro el punto de intersección de las rectas tangentes a ambas circunferencias. La homotecia será directa o inversa, dependiendo de que el centro de homotecia se haya determinado en la intersección de las rectas tangentes interiores o exteriores. Veamos cómo utilizamos esta característica de las circunferencias para resolver algunos problemas de tangencias: • Tangentes comunes exteriores a dos circunferencias Los centros O1 y O2 de dos circunferencias son puntos homotéticos. Dibujamos dos radios paralelos (Fig. 30), uno en cada circunferencia, sobre las que interceptan los puntos homólogos A y A’; la recta de unión de estos puntos, en su intersección con la recta que pasa por los centros de ambas circunferencias, determina el centro de homotecia directa Od de ambas circunferencias. Ruedas tangentes al plano de tierra. Desde Od trazamos las tangentes a la circunferencia de centro O2, tangentes que, prolongadas, lo serán también a la otra circunferencia. Evidentemente, los radios trazados en ambas circunferencias hasta los puntos de tangencia, por ser éstos homotéticos, serán paralelos. Fig. 30 64 Transformaciones geométricas APLICACIONES PRÁCTICAS UNIDAD • Tangentes comunes interiores a dos circunferencias Si los radios paralelos O1A y O2A’ tienen sentidos opuestos (Fig. 31), la intersección del segmento AA’ con la recta de unión de los centros de las dos circunferencias determina el centro de homotecia inverso Oi. Las rectas tangentes trazadas desde Oi a una de las circunferencias, como en el caso anterior, lo serán también a la otra. Los segmentos homólogos que permiten determinar los puntos de tangencia son ahora, además de paralelos, de sentidos contrarios. Fig. 31 • Circunferencias tangentes a dos rectas pasando por un punto, PRR Los centros de las circunferencias buscadas están en la bisectriz del ángulo formado por las dos rectas (Fig. 32). Con centro en un punto cualquiera de esta bisectriz, trazamos una circunferencia auxiliar tangente a las dos rectas. Unimos el vértice O, que será también el centro de homotecia directa entre la circunferencia auxiliar y las circunferencias solución, con el punto dado P interior a las rectas r y s; la recta OP corta la circunferencia Fig. 32 65 3 UNIDAD 3 APLICACIONES PRÁCTICAS Transformaciones geométricas auxiliar en los puntos M y N. A los radios que unen M y N con el centro de su circunferencia les trazamos paralelas desde el punto P; estas paralelas cortan la bisectriz en los puntos O1 y O2, centros de las circunferencias buscadas. Tras determinar los puntos de tangencia en r y s, podemos trazar las circunferencias solicitadas. • Circunferencias tangentes a dos rectas y a una circunferencia situada entre ellas, CRR Si a la circunferencia dada le restamos su radio, queda reducida a su centro, es decir, a un punto; efectuando la misma transformación con las dos rectas (trazar paralelas a cada una de ellas, a la distancia del radio de la circunferencia y a uno u otro lado respecto a cada recta), el problema se ha transformado en trazar las tangentes a dos rectas y un punto, PRR, cuya resolución efectuaremos siguiendo las indicaciones del párrafo anterior. Para cada par de paralelas, por encima o por debajo de las rectas iniciales, el problema tiene dos soluciones, por lo que, en total, el problema planteado puede tener cuatro circunferencias solución que cumplan las condiciones del enunciado. Resolveremos este ejercicio en la próxima unidad, aunque como aplicación de homotecia podríamos resolverlo ahora. 1.2 Aplicaciones de la homología La homología es otra de las transformaciones que permite resolver determinados problemas de geometría plana; tiene también aplicaciones en el sistema diédrico o perspectiva cónica que veremos a continuación: • Transformación homológica de un cuadrilátero cualquiera en un cuadrado Conocemos el cuadrilátero ABCD de la figura 33 y hemos de determinar las características de una homología, vértice, eje y recta límite, que transforme dicho cuadrilátero en un cuadrado. Fig. 33 66 Son conocidas la geometría y las propiedades del cuadrado: lados opuestos paralelos y de igual longitud, diagonales de igual longitud y, por último, los lados contiguos y las diagonales forman entre sí ángulos de 90º. De estas propiedades se derivan las construcciones que se han de realizar para determinar los elementos de la homología. Transformaciones geométricas APLICACIONES PRÁCTICAS UNIDAD Las rectas homólogas de AD y BC serán paralelas, como también lo serán las de AB y CD; esto implica que los lados opuestos del cuadrilátero dado han de cortarse en la recta límite RL, posición, como sabemos, de los puntos cuyos homólogos se hallan en el infinito. De este modo, AD y BC se cortan en un punto M; éste y el punto N de intersección entre AB y CD definen la posición de la recta límite RL. El centro de la homología, punto V, es un punto desde el cual la intersección entre dos lados cualesquiera se vea bajo un ángulo de 90º; de este modo, V estará sobre la semicircunferencia que tiene por diámetro los puntos M y N en que los lados AD y BC cortan la recta límite. El ángulo de 90º entre las diagonales también se halla sobre un arco capaz de 90º, el que tiene por diámetro al segmento PQ, donde P y Q son los puntos de la recta límite de las diagonales AC y BD. La intersección de los dos arcos capaces define la posición del centro V de la homología. Conocido V, los segmentos VN y VM nos marcan las direcciones de dos lados perpendiculares del cuadrado. Paralelamente a RL, y en cualquier posición, situamos el eje de la homología; su posición condiciona el tamaño del cuadrado, que será mayor cuanto más alejado esté del centro V de la homología. Definidos el vértice, la recta límite, el eje y las direcciones de dos lados perpendiculares, completamos la homología del cuadrilátero ABCD que lo transforma en el cuadrado A’B’C’D’. • Secciones planas de superficies radiales de vértice propio Las secciones planas de una superficie radial de vértice propio, pirámide o cono, son homológicas tanto en el espacio como en proyecciones sobre un plano, siendo el vértice de la homología el de la superficie radial y su eje, la recta de intersección entre los planos de las secciones. En el caso, por ejemplo, de una pirámide cuadrangular (Fig. 34), su base puede considerarse como una sección plana, por lo que es homológica de la sección producida en la pirámide por un plano cualquiera. Representamos planta y alzado de la pirámide cuadrangular y las trazas de un plano α. Hallamos la intersección entre una de las aristas laterales de la pirámide, la DV, con el plano α mediante el procedimiento empleado en la unidad 11 de Dibujo técnico 1 al estudiar las intersecciones recta-plano; de este modo, determinamos el punto 1’ perteneciente a la sección producida por el plano α. El resto de vértices de la sección pueden determinarse, en proyección horizontal, repitiendo la intersección de cada una de las aristas laterales con el plano α. Fig. 34 67 3 UNIDAD 3 APLICACIONES PRÁCTICAS Transformaciones geométricas También podemos encontrar los restantes vértices de la sección mediante la aplicación de una homología plana, de la cual conocemos los siguientes elementos (Fig. 35): el vértice V (coincidente con la proyección horizontal del de la pirámide), el eje (coincidente con la traza horizontal hα del plano) y un par de puntos homológicos, D’ y D1’. Resolviendo esta homología, encontraremos los restantes vértices 2’, 3’ y 4’ de la sección plana. La resolución de la homología se ha hecho en una figura independiente para mejorar la claridad de la misma, pero habitualmente se realizaría sobre la misma proyección horizontal de la figura 34; desde ésta se referirían los vértices encontrados a la proyección vertical para tener las dos proyecciones de la sección producida en la pirámide por el plano α. • Trazado de perspectivas cónicas Fig. 35 En la proyección cónica estamos realizando, a través del plano del cuadro, la sección de la pirámide visual que une el punto de vista con una forma cualquiera situada en el plano geometral. Por tanto, la representación en perspectiva que efectuamos sobre el plano del cuadro es la figura homológica de la real situada en el plano geometral; el vértice de esta homología es el punto de vista de la perspectiva cónica, su eje coincide con la línea de tierra, y la línea de horizonte de la perspectiva cónica, con una de las rectas límite en la homología plana. En la figura 36, en relación al eje o LT, abatimos y representamos en verdadera magnitud la forma plana que queremos situar en perspectiva. Desde el punto de vista (centro de la homología), trazamos las direcciones (V)F’, paralela a A’B’, y (V)F, paralela a B’C’; cada una de ellas determina sobre LH o RL la posición de los puntos F y F’, homológicos de los puntos del infinito de la figura. Prolongamos los lados de la figura hasta LT y, desde los puntos de corte con ella, trazamos las rectas homológicas concurrentes, según la dirección, en F o F’. Por último, determinamos A’ y B’ que, con los puntos de los que son homológicos, estarán alineados con (V). Fig. 36 68 Transformaciones geométricas APLICACIONES PRÁCTICAS UNIDAD 1.3 Aplicaciones de la afinidad Al considerar la afinidad como un caso particular de homología con el vértice de la misma en el infinito, las rectas concurrentes en el centro de homología serán ahora paralelas entre sí (concurrentes en un punto impropio). Veamos algunas aplicaciones de esta transformación. • Transformación afín de la circunferencia en elipse Conocemos los diámetros conjugados AB y CD de la elipse (Fig. 37); trazamos la circunferencia de diámetro AB que representa, al mismo tiempo, el eje de la afinidad. Los puntos afines de los extremos del diámetro C’D’ de la circunferencia son los extremos C y D del segundo diámetro conjugado de la elipse; de este modo tenemos definida la dirección de afinidad CC’ y DD’. Por puntos arbitrarios del diámetro AB, trazamos perpendiculares al mismo hasta interceptar puntos sobre la circunferencia; los puntos afines de estos últimos se hallarán sobre las paralelas al diámetro menor de la elipse, trazadas por los mismos puntos de AB, mediante paralelas a la dirección de afinidad CC’. Obtenidos una serie de puntos afines de los de la circunferencia, completamos a mano alzada el trazado de la elipse. Fig. 37 • Secciones planas de superficies radiales de vértice impropio Las secciones planas de una superficie radial de vértice impropio, prisma o cilindro, son figuras afines tanto en el espacio como en proyecciones sobre un plano. La dirección de afinidad viene definida por el conocimiento de un par de puntos afines y el eje de la afinidad es la recta de intersección entre los planos de las secciones. En el caso, por ejemplo, del prisma cuadrangular de la figura 38, su base es la sección producida por el plano horizontal de proyección, por lo que ésta es afín de la sección producida en el prisma por otro plano cualquiera, siendo el eje de la afinidad la intersección del segundo plano con el horizontal de proyección, es decir, su traza horizontal. Representadas las proyecciones del prisma y las trazas del plano, obtenemos la intersección de una de las aristas laterales, la que parte del vértice C en la figura, con el plano: punto 1’ de la proyección horizontal del prisma. Fig. 38 69 3 UNIDAD 3 APLICACIONES PRÁCTICAS Transformaciones geométricas Los demás vértices del polígono sección los determinamos, mediante la relación de afinidad, en la figura 39. Las aristas laterales del prisma definen la dirección de afinidad, C’1’; los segmentos afines sabemos que han de cortarse en puntos del eje de la afinidad. Tenemos, por tanto, datos suficientes para resolver la afinidad y encontrar los vértices 2’, 3’ y 4’ del polígono sección. • Abatimientos en diédrico o axonometría Entre la forma proyectada sobre un plano y la abatida sobre el mismo, existe una relación de afinidad. El eje de la misma es la charnela del abatimiento, siendo la dirección de afinidad la de las perpendiculares trazadas al eje. Fig. 39 Estos conceptos (abatimiento, charnela) pueden resultarnos ahora incomprensibles, sin embargo, los veremos detenidamente en la unidad 5. Imaginemos la forma plana A’B’C’D’ contenida en el plano α de la figura 40; el cuadrilátero (A), (B), (C), (D) es el abatimiento del anterior sobre el plano horizontal de proyección. Entre ambas figuras existe una relación de afinidad, con las condiciones indicadas en el párrafo anterior, que permite deducir la segunda a partir de la primera. Recomendamos volver sobre esta figura después de estudiar los abatimientos en la unidad 5. 1.4 Resolución de tangencias por inversión Fig. 40 Aplicar la inversión a los datos de un problema de tangencias hace posible su transformación en otros nuevos que permiten resolver, más fácilmente, el problema planteado. Este procedimiento de resolución se complementa con el que se basa en la aplicación de los elementos radicales que veremos en la próxima unidad. • Circunferencias tangentes a una recta y a una circunferencia pasando por un punto, PCR Fig. 41 70 Deseamos trazar las circunferencias tangentes, simultáneamente, a la recta r y a la circunferencia c de la figura 41 y que pasen por el punto dado P. Tomando P como centro de inversión y con una razón de inversión cualquiera, determinamos las figuras inversas de la recta y la circunferencia: la recta se invierte en una circunferencia que pasa por el centro de inversión y la circunferencia en otra circunferencia que no pasa por P. Transformaciones geométricas APLICACIONES PRÁCTICAS UNIDAD A estas dos circunferencias, inversas de las figuras iniciales, trazamos las rectas tangentes comunes (dos exteriores y dos interiores). Estas tangentes, al invertirlas respecto a P, se transforman en circunferencias que mantendrán los puntos de tangencia que habremos referido al centro de inversión P; a partir de ellos, construiremos las circunferencias tangentes solicitadas. En la figura 42 encontramos dos de las circunferencias solución, utilizando las rectas tangentes exteriores a las dos circunferencias inversas. Fig. 42 Con centro en P y un radio cualquiera, trazamos la circunferencia de autoinversión c.ai. Unimos P con el centro O de la circunferencia, obteniendo sobre ella los puntos A y B, extremos de un diámetro; desde estos puntos, trazamos las tangentes a la circunferencia de autoinversión y, desde los puntos de tangencia, las perpendiculares a la recta PO; así determinamos los inversos A’ y B’, extremos de un diámetro que nos permiten trazar la circunferencia inversa c’. Para determinar la circunferencia inversa de la recta, le trazamos, desde P, la perpendicular PD y, desde D, la tangente a la c.ai. La perpendicular desde el punto de tangencia a PD nos determina el inverso D’. Los puntos P y D’ son los extremos de un diámetro que permiten el trazado de la circunferencia inversa r’. 71 3 UNIDAD 3 APLICACIONES PRÁCTICAS Transformaciones geométricas A las circunferencias inversas c’ y r’ les trazamos las tangentes comunes exteriores; estos segmentos, T1’T2’ y T3’T4’, son las figuras inversas de dos de las circunferencias solución. Los inversos de cada uno de estos cuatro puntos de tangencia se hallan, alineados con el centro P de la inversión, sobre la figura correspondiente (circunferencia c o recta r). De este modo, T2 está en la intersección con r de la recta PT2’, o T1 en la intersección con la circunferencia c de la recta PT1’. En el caso de la circunferencia, hay dos puntos de intersección y únicamente uno de ellos es el inverso, que escogeremos de acuerdo a su idoneidad para encontrar la circunferencia tangente. El centro O1 de la primera circunferencia solución se halla en la intersección de la perpendicular a r, trazada por el punto de tangencia T2, con la recta OT1. De forma similar encontraremos el centro O2 de la segunda circunferencia. Fig. 43 A las dos circunferencias inversas les podemos trazar otras dos rectas tangentes comunes, en este caso interiores. En la figura 43 hemos determinado los puntos inversos de los extremos de la tangente T3’T4’, alineados con el centro de inversión P y sobre la figura inicial correspondiente. De este modo, tenemos situados T3 en la circunferencia c y T4 en la recta r; a partir de ellos, determinamos el centro O3 de la circunferencia tangente. Con la tangente T1’T2’ deberíamos encontrar la cuarta circunferencia tangente; pero no siempre las cuatro soluciones posibles se transforman en otras tantas soluciones reales, dependiendo éstas de las posiciones relativas entre los elementos del problema. 72 Transformaciones geométricas Movimientos 1. Dados dos segmentos PQ y P’Q’, hallar el centro de giro que permite transformar el primero en el segundo (Fig. 44). Fig. 44 2. Dadas la recta r y la circunferencia de centro O1 de la figura 45, girar ésta respecto al centro de giro dado, para que la circunferencia sea tangente a la recta. CUESTIONES Y EJERCICIOS UNIDAD 5. Inscribir en el triángulo ABC dado (Fig. 48) un triángulo semejante al también dado PQR. Fig. 48 Homología 6. Encontrar el triángulo homólogo del triángulo ABC, según los datos de la homología dados en la figura 49. Fig. 49 Fig. 45 3. Trasladar la circunferencia de centro O1, según la dirección d dada en la figura 46, para que sea tangente a la recta r. 7. En la homología definida en la figura 50, encontrar el homólogo del punto B. Fig. 46 Fig. 50 4. Dibujar un triángulo equilátero con un vértice situado sobre cada una de las tres rectas paralelas de la figura 47. Fig. 47 8. Determinar el cuadrado homólogo de ABCD, con los datos de la homología facilitados en la figura 51. Fig. 51 73 3 UNIDAD 3 CUESTIONES Y EJERCICIOS Transformaciones geométricas Afinidad 9. Dibujar la figura afín del triángulo ABC de la figura 52. Inversión 12. Dada la inversión definida por el centro O y el par de puntos inversos A y A’, determinar el inverso del punto P respecto al mismo centro de inversión (Fig. 55). Fig. 52 10. Hallar la figura afín del cuadrado ABCD de la figura 53. Fig. 55 13. El punto A – A’ es inverso de sí mismo en una inversión de centro O. Hallar la figura inversa de la circunferencia c respecto al mismo centro de inversión (Fig. 56). Fig. 56 Fig. 53 11. Determinar los ejes de la circunferencia afín de la dada en la figura 54, según una homología de la que conocemos el eje y la dirección, dibujados en la figura, y la razón de la misma -3/2. 14. Hallar la figura inversa de la circunferencia dada, conociendo los inversos de dos de sus puntos, A – A’ y B – B’ (Fig. 57). Fig. 57 Fig. 54 Contenidos básicos de la unidad en formato hipermedia, en el CD. Más actividades en el CD La arquitectura es el juego sabio, correcto y magnífico de los volúmenes bajo la luz. LE CORBUSIER 74