Prueba para diferencia de proporciones

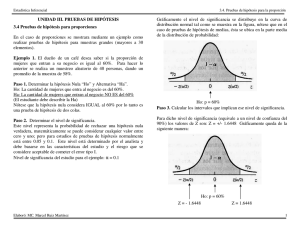
Estadística Inferencial
UNIDAD III. PRUEBAS DE HIPÓTESIS
3.6 Prueba para diferencia de proporciones
En algunos diseños de investigación, el plan muestral requiere
seleccionar dos muestras independientes, calcular las proporciones
muestrales y usar la diferencia de las dos proporciones para estimar o
probar una diferencia entre las mismas.
Las aplicaciones son similares a la diferencia de medias, por ejemplo si
dos empresas consultoras ofrecen datos de proporciones de personas
que van a votar por el PRI y al hacer dos estudios diferentes salen
resultados ligeramente diferentes ¿pero qué tanta diferencia se requiere
para que sea estadísticamente significativo? De eso se tratan las
pruebas estadísticas de diferencias de proporciones.
El estadístico Z para estos casos se calcula de la siguiente manera:
( pˆ 1 -pˆ 2 ) − ( p1 -p 2 )
z=
1 1 
(p ⋅ q) + 
 n1 n 2 
3.6. Prueba para diferencia de proporciones
Ejemplo 1. Una muestra de 87 mujeres trabajadoras profesionales
mostró que la cantidad promedio que pagan a un fondo de pensión
privado el 5% de su sueldo. Una muestra de 76 hombres trabajadores
profesionales muestra que la cantidad que paga a un fondo de pensión
privado es el 6.1% de su sueldo. Un grupo activista de mujeres desea
demostrar que las mujeres no pagan tanto como los hombres en fondos
de pensión privados. Si se usa alfa = 0.01 ¿Se confirma lo que el grupo
activista de mujeres desea demostrar o no?
Paso 1. Determinar la hipótesis Nula “Ho” y Alternativa “Ha”.
Nótese que este problema es de una cola.
Ho: Lo que pagan las mujeres en el fondo de pensión es igual o mayor
a lo que pagan los hombres (algunos autores solo le colocan igual).
Ha: _______________________________________
(El estudiante debe describir la Ha)
La hipótesis alternativa es lo que las mujeres del grupo activista desea
demostrar.
Donde:
n pˆ + n 2 pˆ 2
p= 1 1
n1 + n 2
q=1-p
p̂1 = proporción de la muestra 1.
p̂ 2 = proporción de la muestra 2.
p1 = proporción de la población 1.
p 2 = proporción de la población 2.
n1 = tamaño de la muestra 1.
n 2 = tamaño de la muestra 2.
Elaboró: MC. Marcel Ruiz Martínez
1
Estadística Inferencial
3.6. Prueba para diferencia de proporciones
Paso 2. Determinar el nivel de significancia. Definido por el analista,
en este caso se desea usar α = 0.01
Gráficamente el nivel de significancia se distribuye en la curva de
distribución normal tal como se muestra en la figura:
Paso 3. Calcular los intervalos que implican ese nivel de significancia.
Para dicho nivel de significancia el valor de Z es: Z=-2.326
Gráficamente queda de la siguiente manera:
Z = -2.326
Región
de
rechazo
de Ho
Región de
aceptación
de Ho
Ho: pmujeres ≥ phombres
Región
de
rechazo
de Ho
Región de
aceptación
de Ho
Ho: pmujeres - phombres = 0
Despejando:
Ho: pmujeres - phombres ≥ 0
Para volverlo ecuación algunos
autores toman:
Ho: pmujeres - phombres = 0
Elaboró: MC. Marcel Ruiz Martínez
2
Estadística Inferencial
3.6. Prueba para diferencia de proporciones
Paso 4. Calcular el “estadístico” de la prueba.
Paso 5. Determinar si el estadístico cae dentro de la región que hace la
Hipótesis nula verdadera.
El estadístico Z para estos casos se calcula de la siguiente manera:
( pˆ 1 -pˆ 2 ) − ( p1 -p2 )
z=
1 1 
(p ⋅ q) + 
 n1 n 2 
Donde:
n pˆ + n pˆ
p= 1 1 2 2
n1 + n 2
q=1-p
p̂1 = proporción de la muestra 1.
p̂ 2 = proporción de la muestra 2.
n 2 = tamaño de la muestra 2.
Para el caso del presente ejemplo: considerando la población de
mujeres como 1 y la de hombres como 2 tenemos la siguiente
sustitución:
n1pˆ 1 + n 2 pˆ 2 87(0.05) + 76(0.061)
=
= 0.0551288
n1 + n 2
87 + 76
q = 1 - p = 0.9448712
( pˆ 1 -pˆ 2 ) − ( p1 -p2 )
1 1 
+ 
n
 1 n2 
=
(p ⋅ q)
z=
Región de
aceptación
de Ho
Estadístico de prueba z = -0.3069
p 2 = proporción de la población 2.
n1 = tamaño de la muestra 1.
z=
Región
de
rechazo
de Ho
Ho: µ mujeres - µ hombres = 0
p1 = proporción de la población 1.
p=
Z = -2.326
( 0.05-0.061) − ( 0)
1 1 
+ 
 87 76 
( 0.055129 ⋅ 0.94487 ) 
Como podrá notarse, el estadístico esta DENTRO de la región que hace
verdadera la hipótesis nula.
Paso 6. Aceptar o rechazar la hipótesis nula.
En este caso como el estadístico de la prueba cae DENTRO de la
región que hace verdadera la hipótesis nula, dicha hipótesis se
ACEPTA y se toma como falsa la hipótesis alternativa:
Ho: El porcentaje de su sueldo que pagan las mujeres en el fondo de
pensión es igual a lo que pagan los hombres. (VERDADERO)
Ha: El porcentaje del sueldo que pagan las mujeres en el fondo de
pensión privado es menor a lo que pagan los hombres. (FALSO)
−0.011
= −0.30697
0.0358346
Elaboró: MC. Marcel Ruiz Martínez
3
Estadística Inferencial
A continuación realice los siguientes ejercicios, tenga en cuenta que
puede considerarse de una o dos colas de acuerdo a la naturaleza del
problema:
Dueño de un café. El dueño de un café realizó un estudio estadístico
por cuenta propia y otro usando los servicios de dos practicantes
universitarios que cursan la materia de estadística inferencial. Según
los datos de muestreo del dueño para 30 personas el 60% de los
clientes son mujeres; en cambio en el muestreo realizado por los
estudiantes para 40 personas encontraron que el 70% de los clientes
son mujeres. La pregunta del dueño ahora es si se requiere invertir en
un nuevo estudio dado que alguno de los dos realizados hasta ahora
está mal hecho. Si ambos estudios analizaron una muestra
representativa de la misma población las medias poblacionales son
iguales y no se requiere un estudio adicional. Determine:
a) Hipótesis nula y alternativa
b) Concluya si se requiere un estudio estadístico adicional
basándose en la prueba de hipótesis para proporciones, use un
nivel de significancia de alfa = 0.05.
3.6. Prueba para diferencia de proporciones
Debate político. El gobierno del estado tiene el 50% de aprobación
poblacional tomando como base una muestra de 1000 personas; estos
datos según la empresa consultora A; un partido opositor contrata a la
empresa consultora B y la aprobación que reporta es de 40% tomando
como base una muestra de 1200 personas.
El partido de oposición acusa al gobierno del estado de subirse 10% en
la aprobación ciudadana ¿Será verdad lo que afirma la oposición? Con
un nivel de significancia de 0.05 realice lo siguiente:
a) Planté como hipótesis nula que en efecto la oposición tiene
razón es decir, la diferencia de pestudio B - pestudio A = 0.1 y
confirme si es verdad mediante la prueba de hipótesis.
b) Planté como hipótesis nula que ambos estudios son
estadísticamente independientes es decir, la diferencia de
pestudio B - pestudio A = 0 y confirme si es verdad mediante la
prueba de hipótesis.
Proveedor de focos. Una empresa de fabricación de focos desea
venderle al gobierno del estado; y para concursar con el resto de las
compañías asegura que sus focos son los mas durables del mercado, un
estudio previo de 50 focos de forma aleatoria dio como resultado que
el 94% de los focos duran mas de un año; como el dueño de la empresa
no desea quedarse con ese estudio se contrata otro estudio
independiente y éste indica que el 96% de los focos dura mas de un
año. ¿El primer estudio estuvo mal realizado? Si mediante la prueba de
hipótesis se confirma que las proporciones poblacionales son iguales:
pestudio 1 - pestudio2 = 0 Entonces ambos estudios son estadísticamente
equivalentes. Determine lo siguiente:
a) Defina la hipótesis nula y alternativa
b) Realice la prueba de hipótesis para diferencia de proporciones
con un nivel de significancia de alfa = 0.1
Elaboró: MC. Marcel Ruiz Martínez
4
Estadística Inferencial
Actividad 3.5. Pruebas de hipótesis para diferencia de medias.
Problema 1. Un contratista “A” ha ganado el contrato del gobierno
para colocar los adornos luminosos de navidad; un competidor “B”
acusa de fraude en dicho proceso ya que sus focos técnicamente son
mejores que los del ganador; asegurando que 5% de sus focos duran
mas comparados con los focos del ganador.
Para verificar lo anterior cada contratista ofrece un estudio de duración
realizado de forma independiente, en resumen se ofrecen los siguientes
datos:
Proporción de focos de la empresa A que dura más de 3 años: 70%
Proporción de focos de la empresa B que dura más de 3 años: 75%
Cantidad de elementos muestreados empresa A: 400
Cantidad de elementos muestreados empresa B: 400
Con un nivel de significancia de 0.05 realice lo siguiente:
a) Redacte la hipótesis nula y alternativa; además ¿Será correcto
analizar el problema como una o como dos colas?
b) Con un nivel de significancia de 0.1 determine la veracidad
para la hipótesis nula Ho.
3.6. Prueba para diferencia de proporciones
Problema 2. La proporción de habitaciones ocupadas en un hotel en el
2008 fue de 80% en promedio durante los 365 días del año.
En el 2009 en el mismo hotel la ocupación promedio fue del 85%; de la
misma forma se muestrearon todos los días del año.
Hay un aumento en la cantidad de personas que demandan el servicio
hotelero ¿pero será una diferencia estadísticamente significativa? ¿se
está recuperando y reactivando el turismo? Para comprender lo anterior
realice con un nivel de significancia del 0.005 lo siguiente:
Considere como hipótesis nula que la proporción en ambos años en
realidad es igual y realice la prueba de hipótesis para diferencia de
proporciones.
Elabore una PRÁCTICA DE EJERCICIOS de este trabajo (INDIVIDUAL),
las
rúbricas
se
indican
en
la
liga
siguiente:
http://marcelrzm.comxa.com/Rubricas/Rubricas.htm
SIN EL PROCEDIMIENTO LA ACTIVIDAD NO ES VÁLIDA
Puede enviar el documento final por correo electrónico a las siguientes
direcciones:
[email protected];
[email protected];
[email protected] y [email protected]
No olvide enviarse copia a sí mismo del correo que envía, si usa Outlook
solicite confirmación de entrega y de lectura.
Elaboró: MC. Marcel Ruiz Martínez
5