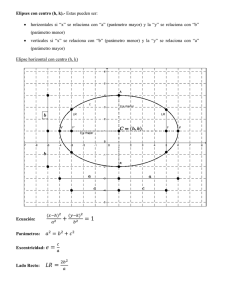
Análisis estadístico de valores extremos y aplicaciones
Anuncio

Realizado por Alejandro Ibáñez Rosales. Trabajo de Investigación. Máster Oficial en Estadística Aplicada. Departamento de Estadística e Investigación Operativa. Universidad de Granada. Octubre 2011. i Trabajo de Investigación realizado por Alejandro Ibáñez Rosales y dirigido por José Miguel Angulo Ibáñez, perteneciente a la Línea de Investigación de Análisis de Características Estructurales de Sucesos Extremos. Aplicación a la Evaluación de Riesgos en Geofísica y Medio Ambiente. En Granada, a 7 de Octubre de 2011. ii ÍNDICE. CAPÍTULO 1: INTRODUCCIÓN. …………………………………………………………………………….. Páginas 1-3. 1.1. Historia de la teoría de valores extremos. . ………………………………………………….. Páginas 1-2. 1.2. Aplicaciones prácticas de los valores extremos. . ……..………………………………….. Páginas 2-3. CAPÍTULO 2: ESTADÍSTICOS DE ORDEN. . ……..………………...………………………………….. Páginas 4-8. CAPÍTULO 3: LA DISTRIBUCIÓN DE VALORES EXTREMOS GENERALIZADA…………… Páginas 9-62. 3.1. Introducción. El Teorema de Valores Extremos………………………………………….. Páginas 9-11. 3.2. Características de la Distribución de Valores Extremos Generalizada. ……… Páginas 11-12. 3.3. El caso del mínimo. ……..………………...……………………………………………………….. Páginas 12-13. 3.4. Ejemplos de distribuciones teóricas de la Distribución GEV. …………………… Páginas 13-16. 3.5. Simulación de valores de Distribuciones GEV. . ………………………………………… Páginas 16-24. 3.6. Ejemplos con datos reales. ....…………………………………………....……………………..Páginas 24-33. 3.7. Distribuciones relacionadas con la Distribución de Valores Extremos Generalizada …………………………………………………………………………………………………..Páginas 33-47. 3.7.1. Distribución de Fréchet. ……………………………………………………………………… Páginas 33-38. 3.7.1.1. Características. ………………………………………………………………………………… Páginas 33-35. 3.7.1.2. Representaciones gráficas. …………………………………………………………….… Páginas 35-38. 3.7.2. Distribución de Gumbel..……………………………………………………….…………….. Páginas 38-43. 3.7.2.1. Características. ………………………………………………………………………..…….… Páginas 38-39. 3.7.2.2. Representaciones gráficas. ……………………………………………………..…….… Páginas 39-42. 3.7.2.3. Distribución de Gumbel para el mínimo. …………….…………………..…….… Páginas 42-43. 3.7.3. Distribución de Weibull....…………….……………………………………………………..… Páginas 43-47. 3.7.3.1. Características….…………….……………………………………………………………….… Páginas 43-44. 3.7.2.3. Representaciones gráficas. .…………………………………………………………….… Páginas 44-47. 3.8. Niveles de retorno. Estudio gráfico de la bondad del ajuste. …………………… Páginas 47-48. 3.9. Estimación de los parámetros por Máxima Verosimilitud………………………………… Página 48. 3.10. Ejemplos con bloques y con análisis gráficos…………………………………………… Páginas 48-62. iii CAPÍTULO 4: MODELOS DE UMBRALES………………………………………………………….. Páginas 63-90. 4.1. Excedencias. …………………………………………………………….……………………………… Páginas 63-70. 4.2. La Distribución de Pareto Generalizada. ……………….……………………………..…… Páginas 70-73. 4.3. Ejemplos. ……………….….…..…………………….……………………………..…………………. Páginas 73-90 4.3.1. Datos simulados. ……………….….…..…………………….……………………………..…… Páginas 73-79. 4.3.2. Representación de distribuciones de Pareto generalizadas teóricas………. Páginas 79-81. 4.3.3. Ejemplos con datos reales…………………………………………………………………….. Páginas 81-90. CAPÍTULO 5: OTROS ASPECTOS.………… ………..……………………………………..………….. Páginas 91-95. 5.1. Valores Extremos en series estacionarias. …………………………………………….. Páginas 91-92. 5.2. Valores Extremos en series no estacionarias. …………………………………………………. Página 92. 5.3. Caso de variables no independientes ni idénticamente distribuidas…………. Páginas 92- 93. 5.4. Caso multivariante. . …………………..…………………………………………………………….…… Página 93. 5.5. Extremos espaciales. ………………………………………………………………………………………Página 94. 5.6. Teoría bayesiana aplicada a valores extremos………………………………………………….Página 94. 5.7. Procesos puntuales ………………………………………………………………………………………….Página 94. 5.8. Caso de colas pesadas ……………………………………………………………………………………. Página 95. BIBLIOGRAFÍA…………………………………………………………………………………………..…….. Páginas 96-98. iv CAPÍTULO 1: INTRODUCCIÓN. 1.1. Historia de la teoría de valores extremos. Los valores extremos ha constituido desde hace bastante tiempo una disciplina de gran interés, y no sólo para estadísticos sino, entre otros, para científicos e ingenieros. Existen varias definiciones en la literatura sobre este tema acerca de qué trata la teoría de valores extremos, pero esencialmente casi todas dicen lo mismo. Para Coles (2001), la teoría de valores extremos es una disciplina que desarrolla técnicas y modelos para describir los sucesos menos comunes, lo cual, para él, hace que sea una disciplina “única”. En cambio, para Gumbel (1958, autor del considerado durante mucho tiempo libro de referencia para el estudio de valores extremos), el objetivo de la teoría de valores extremos es analizar valores extremos observados y predecir valores extremos en el futuro. Una definición más simplista que mencionan algunos autores es decir que los valores extremos son “el máximo y el mínimo”. Para Albeverio, Jentsch y Kantz (2005), la interpretación de lo que es algo “extremo” es complicada ya que su definición engloba varios atributos tales como “excepcional”, “sorprendente” y “catastrófico”. Según dichos autores, al ser como se ha dicho subjetivamente difícil definir a los valores extremos, es mejor caracterizarlos mediante, por ejemplo, sus propiedades estadísticas, observaciones, predictibilidad, mecanismos, etc. Respecto a la antigüedad de esta teoría, Leadbetter, Lindgren y Rootzen (1983) afirman que puede decirse que tiene alrededor de 80 años de antigüedad, aunque el origen la teoría de valores extremos es bastante más antiguo. Por su parte, Coles afirma que no fue hasta 1950 cuando se propuso una metodología seria para modelizar sucesos de este tipo. Asimismo, también dice que las primeras aplicaciones fueron en el campo de la ingeniería civil, pues según él los ingenieros siempre han necesitado diseñar sus estructuras de forma que éstas soportaran las distintas fuerzas que podrían afectarlas (refiriéndose principalmente a fuerzas de la naturaleza). En cambio, Según Kotz y Nadarajah (2001), el origen de la teoría extremos tiene bastante relación con los astrónomos, pues éstos necesitaban usar dicha teoría para tratar con observaciones atípicas en sus estudios. Es también interesante comentar que, tal y como afirman De Haan y Ferreira (2006), la teoría asintótica de valores extremos se ha estudiado paralelamente a la del Teorema Central del Límite, de ahí que ambas teorías tengan bastante semejanza. Para ambos autores, la teoría de extremos para muestras está relacionada con el comportamiento límite del o del cuando n tiende a infinito. Algunos autores señalan que la teoría de valores extremos tuvo como precursor a Leonard Tippet, empleado de la British Cotton Industry Research Association, donde trabajaba para construir hilos de algodón más fuertes. En sus estudios, durante los años 20, se dio cuenta de que la fuerza de un hilo dependía de la fuerza de sus fibras más débiles. Pero en cambio, según Gumbel, el pionero a la hora de estudiar los valores más grandes para otras distribuciones fue E. L. Dodd, en 1923, aunque pocos siglos antes ya se habían empezado a estudiar los extremos a través de la distribución Normal. También dice que el primer texto sobre distribuciones 1 diferentes de la Normal se debe a M. Fréchet (1927), quién también fue el primero en obtener la distribución del máximo; y asimismo menciona que Bernouilli también estudió los valores extremos cuando éste investigó sobre la distancia media más larga desde el origen hasta n puntos representados aleatoriamente. 1.2. Aplicaciones prácticas de los valores extremos. Los valores extremos tienen muchas aplicaciones en la práctica. Algunas aplicaciones de la teoría de valores extremos, según Kotz y Nadarajah (2001, autores que además definen a la teoría de valores extremos como algo “curioso y fascinante”) son ráfagas de viento, contaminación en el aire y análisis de corrosión. El matemático de origen húngaro Janos Galambos (1978) menciona otros ejemplos de extremos como inundaciones, sequías, efectos de aditivos en alimentos, etc. También Reiss y Thomas (1997) mencionan otras aplicaciones, como el estudio de la longevidad de la vida humana, la gestión de tráfico (en telecomunicaciones), la resistencia de materiales (respecto a este caso, Galambos dice que la fuerza de una lámina de metal es el mínimo de las fuerzas de las piezas que forman la lámina), la concentración de ozono, geología o meteorología (lluvias, vientos, etc). Un ejemplo concreto, mencionado por Coles, es el siguiente: supóngase que, como parte de los criterios para el diseño de defensas costeras, se necesita un rompeolas para protegerse de todos los niveles del mar que se espera que haya durante 100 años. Según Coles, posiblemente haya disponibles datos locales de niveles del mar, pero para un periodo mucho más corto de, por ejemplo, 10 años. Lo qué para él es interesante es estimar qué niveles del mar se pueden alcanzar en los 100 siguientes años usando los datos de los 10 años anteriores, y para hacer extrapolaciones de este tipo se usará el marco de trabajo de la teoría de valores extremos. Otro ejemplo más concreto es el del terremoto de Lisboa de 1755, que es mencionado por algunos autores como un suceso muy poco común que se puede modelizar mediante la teoría de valores extremos. Dicho terremoto tuvo lugar el 1 de noviembre de ese año, sobre las 10:16 A.M., y causó la muerte de entre 60.000 y 100.000 personas. Además, fue seguido por un maremoto y un incendio, y Lisboa fue destruida casi del todo. Otro terremoto devastador y más reciente, mencionado por Castillo, Hadi, Balakrishnan y Sarabia (2004), fue el de Bam (India) en 2003, que tuvo lugar el 26 de diciembre de ese año y en el que hubo más de 26.000 muertos y de 30.000 heridos. Para sucesos catastróficos como éstos se podrían haber evitado las catástrofes, o al menos se habría podido estar mejor preparados. Galambos también menciona otro ejemplo, que es el del tiempo de servicio. Se considera un equipo con un gran número de componentes, y se supone que los componentes pueden prestar servicio simultáneamente. Entonces el tiempo que se necesita para que el equipo preste servicio viene determinado por el componente que tarda más tiempo en servir. Este autor también piensa que los desastres naturales no se pueden evitar completamente, pero que sí se pueden tomar precauciones para minimizar sus efectos, y ahí es donde la teoría de valores extremos puede ayudar. 2 Particularmente interesante es el ejemplo que mencionan Albeverio, Jentsch y Kantz (2005) y sobre el cual detallan bastante. Dicho ejemplo trata sobre la epilepsia, que se considera como “un valor extremo dentro del cerebro humano”. Los mencionados autores también hablan de que desde hace milenios ya se estudiaban los valores extremos, como en el Río Nilo, donde se lleva 5000 años estudiando los niveles de tal río. Otro ejemplo interesante lo mencionan de Haan y Ferreira, y es el siguiente: Un neumático de un coche puede estropearse de dos formas. Por cada día que se use el coche, el neumático se desgastará un poco más, y con el paso del tiempo y como consecuencia del deterioro acumulado, el neumático acabará rompiéndose. Pero también puede ocurrir que al conducir se pise un bache, o que el coche golpee la acera. Puede pasar que esos accidentes no tengan efectos en los neumáticos, o que el neumático termine perforado, en cuyo caso sólo una observación sería la que causara un fallo, lo que significa que el máximo parcial supere cierto umbral. Por último, un ejemplo relacionado con éste lo mencionan Castillo, Hadi, Balakrishnan y Sarabia (2004). Y es sobre la velocidad máxima a la que circulan vehículos en una parte concreta de la carretera\autopista, ya que en función de esos datos se puede decidir el uso de coches patrulla por dicha zona. U otro ejemplo muy parecido sería el número máximo de vehículos que circulan por una intersección a una hora punta, pues el conocer dicho máximo facilitaría un mejor control del tránsito vehicular. 3 CAPÍTULO 2: ESTADÍSTICOS DE ORDEN. Antes de empezar a tratar la distribución de valores extremos, es interesante ver definiciones relativas a los estadísticos de orden; dichas definiciones son bastante similares en todos los textos que tratan sobre este tema. En Estadística, se suele considerar el estadístico de orden k de una muestra estadística como el k-ésimo valor más pequeño. Por ejemplo, en una muestra de tamaño 25, el estadístico de orden k = 9, sería el noveno valor más pequeño de dicha muestra. Los estadísticos de orden tienen bastante importancia dentro de la Estadística no paramétrica y de la inferencia. Así, si se tiene una muestra aleatoria simple de tamaño n, ,y es una realización de esa muestra, el mínimo es siempre el valor más pequeño de la muestra, esto es, ; mientras que el máximo es el valor más grande de la muestra . Ejemplo 1: Se tiene la muestra de tamaño 6 siguiente: 45, 23, 67, 33, 101, 122. Los valores de dicha muestra se escriben de la siguiente forma: x1=45, x2=23 x3=67, x4=33, x5=101 y x6=122. Los estadísticos de orden para esa muestra se escribirían de la siguiente forma: x(1)=23, x(2)=33 x(3)=45, x(4)=67, x(5)=101 y x(6)=122. Así, en esa muestra, el mínimo sería x(1), que vale 23 y el máximo x(6) (122). También es posible calcular el mínimo y máximo de una muestra con el paquete estadístico R: Ejemplo 2: Se genera una muestra de tamaño 35 de una Normal de media 9 y desviación típica 2. La sintaxis en R para general tal muestra es la siguiente: Mientras que los valores generados son los siguientes: Y a continuación se calculan el máximo y el mínimo: 4 Como se puede ver, el máximo es 12.64673 (séptimo valor de la muestra), mientras que el mínimo es 4.253601 (valor 29 de la muestra). En el caso de variables aleatorias, si se tiene una secuencia de n variables aleatorias , los estadísticos de orden también son variables aleatorias, que se definen ordenando las realizaciones de en orden ascendente. Comúnmente, las variables aleatorias , que forman una muestra, suelen considerarse independientes e idénticamente distribuidas. Otro estadístico de orden también importante es el rango, que es la diferencia entre el valor más grande y el más pequeño: Dicho estadístico da una medida de la dispersión de los valores. Ejemplo 1.2: En el primer ejemplo anterior, Ejemplo 2.2: Mientras que en el segundo ejemplo anterior, Por último, otro estadístico de orden bastante conocido es la mediana: Ejemplo 1.3.: Para el primer ejemplo, la mediana es Ejemplo 2.3.: Mientras que para el segundo, se va a calcular la mediana utilizando R: Como se puede ver, la mediana es casualmente el primer valor de la muestra, 9.064752. y vale Una ventaja que tiene la mediana muestral frente a la media muestral, es que la primera es menos sensible a observaciones extremas. Esto se puede comprobar en el ejemplo anterior donde la muestra tiene tamaño 6; para dicha muestra, la mediana, ya calculada anteriormente, es 51, mientras que la media es la siguiente: A continuación, se va a cambiar el último valor de la muestra, que va a pasar a ser bastante más grande, en concreto, x6=896. Con lo cual, la muestra queda de la siguiente forma: 5 x1=45, x2=23 x3=67, x4=33, x5=101 y x6=896. La media ahora es: Como se puede ver, la media ha aumentado considerablemente. Ahora se va a calcular la mediana para esa misma muestra “modificada”. En este caso, vale que coincide con la mediana anterior, antes de cambiar el último dato de la muestra. Así, este ejemplo sirve para demostrar cómo la media es mucho más sensible a los valores extremos que la mediana, pues al haber sido el valor más grande el que se ha cambiado, y al usarse para calcular la mediana solo los valores centrales, la mediana no sufre cambio. Si se tiene una m.a.s. (muestra aleatoria simple), es posible calcular la distribución del máximo y del mínimo. Para el máximo, es la siguiente: donde se ha usado las propiedades de independencia, y el que el suceso “que el mínimo sea mayor que x” equivale a “que todos los valores sean mayores que x”. Sin más que derivar, se deduce fácilmente la función de densidad: Para el máximo, su función de distribución es la siguiente: donde se han usado también las propiedades de independencia, y el que el suceso “que el máximo sea menor o igual que x” equivale a “que todos los valores sean menores o iguales que x”. En este caso, a función de densidad es la siguiente: Ejemplo 3: Se tiene una muestra aleatoria simple de tamaño 52 de una variable aleatoria con distribución exponencial de parámetro y se quiere calcular la función de densidad tanto del mínimo como del máximo. La función de densidad de una variable aleatoria con dicha distribución viene dada por: Mientras que la función de distribución es 6 Para el máximo, la función de distribución es mientras que la función de densidad viene dada por En cambio, para el mínimo la función de distribución es ; la función de densidad, por su parte, viene dada por =13 Otras distribuciones de interés relativas a estadísticos de orden son las siguientes: Distribución conjunta del máximo y del mínimo: Dada una muestra de tamaño n, la distribución conjunta del máximo y del mínimo, esto es, del vector aleatorio , viene dada por Distribución conjunta de dos estadísticos de orden r y s, con r menor que s. Dada una muestra de de tamaño n, la distribución conjunta de dos estadísticos de orden r y s cualesquiera viene dada por Distribución conjunta de dos estadísticos de orden consecutivos. Dada una muestra de tamaño n, la distribución conjunta de dos estadísticos de orden consecutivos y ( con i siendo un entero positivo mayor o igual que 1 y menor que n) viene dada por Ejemplo 4: Si se tiene una muestra de tamaño n=10, la distribución conjunta de viene dada por y Distribución conjunta de todos los estadísticos de orden: La distribución conjunta de todos los estadísticos de orden es: 7 Distribución conjunta de los k primeros estadísticos de orden: La distribución conjunta de los k primeros estadísticos de orden viene dada por Distribución conjunta de los k últimos estadísticos de orden: Por último, la distribución de los k últimos estadísticos de orden es: = 8 CAPÍTULO 3: LA DISTRIBUCIÓN DE VALORES EXTREMOS GENERALIZADA. 3.1. Introducción. El Teorema de Valores Extremos. En este capítulo del trabajo se va a ver la distribución de Valores Extremos Generalizada (en inglés, Generalized Extreme Value distribution, cuyas siglas son GEV), que también es conocida como la distribución de Fisher-Tippett, la distribución tipo von Mises-Jenkinson o la distribución de valores extremos tipo von Mises. Según Kotz y Nadarajah, dicha distribución fue inicialmente introducida por Jenkinson (1955). Sean variables aleatorias, el máximo de dichas variables. Según Coles, en ocasiones, en la práctica las (que tienen una función de distribución común F) corresponden a valores de un proceso medido en una escala regular de tiempo –como medidas de niveles del mar cada hora, o temperaturas medias diarias- de forma que representa el máximo del proceso sobre n unidades temporales de observación. Si por ejemplo, n es el número de observaciones en un mes, entonces corresponde al máximo mensual. La función de distribución de (que es como la gran mayoría de autores denotan al máximo de ) se dedujo anteriormente en el capítulo sobre estadísticos de orden, y es: Según de Haan y Ferreira (2006), dicha función converge en probabilidad a 0 si y a 1 si donde Por tanto, para que la distribución límite no sea degenerada, hay que tipificar, esto es, encontrar sucesiones de constantes a n>0 y bn (n = 1, 2,…) de forma que la expresión tenga una distribución no degenerada cuando esto es, que . Se trata de “estandarizar” la variable variable estandarizada se le llama mediante una transformación lineal. A la nueva Así, se tiene el siguiente teorema, conocido como Teorema de Valores Extremos o Teorema de Fisher-Tippett-Gnedenko: -Teorema 1: Si existen sucesiones de constantes y de forma que cuando donde G es una función de distribución no degenerada, entonces G pertenece a una de las siguientes familias: 9 I: II: III: para parámetros y, en el caso de, las familias II y III, Estas tres clases de distribuciones son conocidas como las distribuciones de valores extremos, donde las de tipo I son la familia de Gumbel; las de tipo II la de Fréchet, y las de tipo III la de Weibull, cada una con su parámetro de localización b y de escala, a; y además, las familias de Fréchet y de Weibull tienen un parámetro de forma Más adelante se estudiarán las características de esas distribuciones, y se profundizará más en ellas. La interpretación del teorema es la siguiente: cuando se pueden encontrar sendas sucesiones que verifiquen lo anterior, entonces la distribución asintótica de la variable transformada es de alguno de los tres tipos anteriores. A su vez, se deduce que la distribución de sólo puede ser una de esas tres. Sin duda, este teorema es posiblemente considerado como el más importante, y si no de los que más, dentro de la teoría de valores extremos; de hecho Coles afirma que el teorema anterior es un análogo para valores extremos del Teorema Central del Límite. Todas las distribuciones anteriores se pueden condensar en una sola, que es la Distribución de Valores Extremos generalizada (GEV), cuya función de distribución es la siguiente: para A continuación, se define la noción demáximo-estabilidad, definición que es importante para la teoría de valores extremos. Existen varias definiciones posibles (aunque todas son bastante parecidas), y una de ellas es la siguiente: -Definición 1: Sean variables aleatorias independientes e idénticamente distribuidas con función de distribución F. Se dice que la función de distribución F es máximo-estable si para alguna elección de constantes y real, P . Dos definiciones relacionadas con las anteriores son las siguientes: -Definición 2: Una distribución univariante se dice que pertenece al dominio máximo de atracción de una función de distribución G, y se denota por , si cumple lo siguiente: I. G es una distribución no-degenerada. II. Existen sucesiones y que verifican P 10 -Definición 3: Dos funciones de distribución F y G se dicen que son distribuciones con colas equivalentes si se cumple que para ciertas constantes y donde , donde es el punto final derecho Para el mínimo existe un análogo de las distribuciones máximos-estables para el máximo; se trata de las distribuciones mínimo-estables. La definición es también análoga: -Definición 4: Sean … variables aleatorias independientes e idénticamente distribuidas con función de distribución F. Se dice que la función de distribución F es mínimoestable si para alguna elección de constantes y real, se cumple que P 3.2. Características de la Distribución de Valores Extremos Generalizada. La familia de distribuciones de valores extremos generalizada, como se vio antes, tiene la siguiente función de distribución: definida en con y tres parámetros: el parámetro de localización; parámetro de forma. El modelo tiene el parámetro de escala; y que es el La función de densidad de esta distribución de probabilidad es la siguiente: de nuevo definida en Otras características de la distribución de valores extremos generalizada son las siguientes: Esperanza matemática. donde es la función Gamma, y es la constante de Euler. 11 Varianza. donde Cuantil de orden p. Mediana. Moda. Coeficiente de Asimetría. (donde es la función zeta de Riemann). Coeficiente de Curtosis. Algunas distribuciones que están relacionadas con la distribución de valores extremos generalizada son las siguientes: Si una variable X se distribuye según una , entonces la transformación lineal sigue también una distribución de valores extremos generalizada, pero con parámetros Ejemplo 1: Sea distribución de . Entonces, si se tiene la transformación la es Si una variable X está distribuida según una Exponencial de parámetro 1, la transformación sigue una Ejemplo 2: Sea y sea la transformación Entonces, 3.3. El caso del mínimo. Para estudiar el mínimo, el procedimiento es análogo; simplemente se usa que Si se denota al mínimo por entonces su distribución es la siguiente: 12 definido en y donde Igual que para el máximo, existe un teorema que permite aproximar la distribución de la función de distribución anterior: -Teorema 2: Si existen sucesiones de constantes y por de forma que cuando donde es una función de distribución no degenerada, entonces distribuciones de valores extremos generalizada para el mínimo: Si es de la familia de en el caso en el que Si , para . Y la función de densidad es: , Definida en si o si Si El cuantil de orden p para dicha distribución viene dado por: También existen modelos para el r-ésimo estadístico más grande, que en algunos casos pueden ser bastante interesantes y útiles. 3.4. Ejemplos de distribuciones teóricas de la distribución GEV. A continuación, se van a representar valores teóricos de la distribución GEV para el máximo, para diferentes valores de los tres parámetros. Dichos gráficos han sido generados con el 13 software para ajustar distribuciones de probabilidad EasyFit, del cual se puede obtener una versión en prueba gratuita a través de Internet: Primero se ha representado la función de densidad teórica y la función de distribución de una GEV(-2, 3, 0). Como se puede ver, esta distribución concreta es asimétrica negativa, pues la mayoría de los valores están concentrados a la izquierda. Ahora la distribución representada es una GEV(1, 0.5, 0), esto es, con parámetro que corresponde a la distribución de Gumbel. Aquí, la distribución está también más inclinada hacia la izquierda, y se puede ver que está centrada en el parámetro de localización, que vale 1. Ahora la GEV (1, 1, -3) tiene una forma bastante distinta a las dos anteriores. 14 De nuevo la distribución representada, GEV(1, 1, 0), es ahora una Gumbel, sólo que ahora el parámetro de escala es mayor, concretamente el doble. Viendo la escala de los datos en un gráfico y otro se puede observar dicha diferencia de escala. En este caso los gráficos corresponden a una GEV(1, 1, 3). La diferencia ahora se nota sobre todo en la función de distribución, que crece de forma claramente distinta a las anteriores. También es destacable la forma de la función de densidad: al contrario que para la GEV(1, 1, 3), ahora la densidad, que también es algo aplanada, se concentra mayoritariamente en la parte izquierda de la distribución; lo cual se explica con el cambio del parámetro de forma, que ha pasado de ser -3 a ser 3. Ahora la distribución representada es una GEV(1, 3, 0), se puede apreciar el cambio de escala respecto a la GEV (1, 0.5, 0) y respecto a la GEV(1, 1, 0). 15 Por último, se ha representado una GEV(3, 1, 2). Como suele ocurrir, la mayor masa de probabilidad está concentrada en torno al parámetro de localización, y está también aplanada por la parte izquierda aunque no tanto como la GEV(1, 1, 3), porque ahora el parámetro de forma es menor. 3.5. Simulación de valores de distribuciones GEV. En este apartado, usando el paquete estadístico R se van a simular valores de variables aleatorias cuya distribución sea la de valores extremos generalizada. Para ello, se descarga el paquete llamado “extRemes”, bastante útil y que, como su nombre indica, sirve para estudiar aspectos relacionados con los valores extremos. Entre otras cosas, el paquete permite simular valores de una variable con distribución GEV para unos parámetros dados. Así, por ejemplo, se va a comenzar simulando una variable con distribución y sin tendencia. Los datos, que se almacenan con el nombre de “datos1”, son los siguientes: El gráfico de los 100 datos generados es el siguiente: 16 Ahora se van a generar datos de una misma distribución, pero que presente una tendencia de 0.5. Los valores generados (almacenados como “datos2”) son los siguientes: El gráfico de los datos es el siguiente: 17 A la vista del gráfico se observa claramente la tendencia ascendente que se ha introducido. En cambio, ahora se va a cambiar el valor del parámetro de escala. Primero se va a simular una Los valores simulados (“datos3”) son los siguientes: Y el gráfico con los valores generados se puede ver a continuación: 18 Ahora se cambia el parámetro de escala, que pasa a ser 4, con lo cual se va a trabajar con una Los valores simulados de esa distribución (“datos4”) son: Mientras que esos valores representados en un gráfico se pueden observar a continuación: 19 Se puede ver claramente el cambio de escala, pues para esta muestra generada los valores están en una escala mayor. Ahora se va a modificar el parámetro de localización. Se va a generar una (“datos5”): La representación gráfica de los 100 valores generados es la siguiente: 20 Y ahora se cambia el parámetro de localización, que pasa a ser =3.5, con lo cual la distribución que se tiene ahora es una . Los datos que se han generado (“datos6”) se muestran a continuación: La representación gráfica de esta serie de valores generados es la siguiente: 21 Se ve que al cambiar el parámetro de localización, ahora los valores generados son más pequeños que los anteriores. Y para terminar, se van a generar valores de distribuciones con el mismo parámetro de localización y de escala, pero distinto de forma. La distribución de la cual se generan primero los valores es una . Esos valores (“datos7”), son los siguientes: Seguidamente, se pueden ver dichos datos representados gráficamente: 22 Finalmente, se genera una . Los datos (“datos8”), son los siguientes: El gráfico de los datos se puede ver a continuación: 23 Se observa un cambio en la forma de la distribución los datos al modificar el valor del correspondiente parámetro. Un punto de vista interesante que proponen varios autores dentro de la teoría de valores extremos es el de usar bloques de máximos para el estudio de valores extremos, esto es, dividir los datos en bloques de igual longitud, para luego obtener máximos por bloque, y ajustar la distribución de valores extremos generalizada bloque a bloque. Lo más normal es que los bloques se elijan de longitud igual a un año, por ejemplo en el caso de datos mensuales. Ese método se conoce como el método de Gumbel. 3.6. Ejemplos con datos reales. Ejemplo 3: Se tienen datos (fuente: Australian Boureau of Statistics, ABS) correspondientes al número de personas sin empleo en Australia desde Enero de 1979 hasta Diciembre de 1994. Como se puede ver, se trata de datos mensuales durante 16 años, y se quieren dividir los datos en bloques para estudiar el máximo por bloques. Al ser los datos, mensuales, lo ideal es que los bloques de máximos sean máximos anuales; luego, para cada año, los datos en ese año formarán un bloque. Los datos, desglosados por año y mes, son los siguientes: 24 Como se puede ver, cada fila corresponde a un bloque. A continuación, se van a agrupar los datos por variables, correspondiendo cada variable a un bloque y formándose los bloques por orden: En total, son 16 bloques, cada uno de tamaño igual a 12, una observación mensual. A continuación se muestran los valores por cada bloque, junto a la representación gráfica del bloque en cuestión: 25 26 27 28 29 30 31 32 3.7. Distribuciones relacionadas con la distribución de Valores Extremos Generalizada. 3.7.1. Distribución de Fréchet. 3.7.1.1. Características. Es un caso especial de la distribución de valores extremos generalizada. Su función de distribución, cuando se tienen tres parámetros, viene dada por 33 si ,mientras que la función de densidad es donde es el parámetro de forma, el de escala y localización. Cuando se tienen dos parámetros (en el caso en el que distribución pasa a ser el de , la función de y la función de densidad es Por último, cuando la distribución sólo tiene un parámetro , y El nombre de la distribución viene del matemático francés Maurice Fréchet, y su principal uso es en el campo de la hidrología. Algunas características de esta distribución son las siguientes: Media siempre que Varianza siempre que Moda Coeficiente de asimetría si Coeficiente de curtosis Primer Cuartil Mediana Tercer Cuartil Las características para la distribución de Fréchet con dos parámetros y con uno se pueden calcular sin más que sustituir en las expresiones anteriores los valores y La distribución de Fréchet está relacionada con las siguientes distribuciones: Si entonces . 34 Ejemplo 5: Sea e Y= Si Entonces Y entonces Ejemplo 6: Sea e Y=4X-2. Entonces Si e Ejemplo 7: Sea e entonces Entonces . Si Ejemplo 8: Sea entonces Entonces 3.7.1.2. Representaciones gráficas. A continuación se representa la función de densidad y de distribución de una variable aleatoria con distribución de Fréchet, variando el parámetro: En primer lugar se ha representado una Fréchet(2, 2), esto es, con parámetro de localización igual a 0; al ser dicho parámetro 0, la función de densidad está representada para valores mayores que 0. Se puede ver que es asimétrica hacia la izquierda. 35 Ahora la distribución representada es una Fréchet(2,3), ha cambiado el parámetro de escala que ha pasado a valer 3. Se puede ver que la forma del gráfico es parecida, pero con el cambio de la escala presente en esta nueva representación gráfica. Igualmente, se puede ver que la función de distribución también tiene una forma parecida, sólo que ahora empieza a crecer significativamente antes de llegar al valor x = 2, cuando para la distribución anterior dicho crecimiento comenzaba a producirse antes de llegar a x = 1. En esta nueva representación se ha introducido un parámetro de localización que vale 1, luego la variable está representada para valores más grandes que dicho valor. La forma es exactamente igual que para la distribución anterior, sólo que ahora se ha desplazado el gráfico una unidad hacia la derecha fruto del mencionado cambio del parámetro de localización. Si se compara la Fréchet(3, 2) aquí representada con la Fréchet(2, 2) anterior se aprecia un cambio evidente de forma en los datos 36 Ahora se ha cambiado el parámetro de escala respecto al caso anterior, y se ve que el gráfico tiene la misma forma pero hay cambio en la escala, pues al aumentar el valor del parámetro el gráfico se achica algo más. Nuevamente se ha introducido un parámetro de localización, con lo cual tanto la función de densidad como la de distribución existen para valores mayores a dicho parámetro, que ahora vale 1. Comparando con la Fréchet (3,3) (o Fréchet(3, 3, 0)), la distribución está desplazada una unidad hacia la derecha, siendo la forma y la escala exactamente iguales. Aquí el parámetro de localización vuelve a ser 0, luego nuevamente los valores de esta distribución están por encima de 0. La distribución es algo asimétrica hacia la izquierda. 37 En este nuevo cambio de escala se ve otra vez cómo la distribución se achica, ya que por ejemplo, para la Fréchet(4,2), el valor x = 2 tiene asociado f(x)=0.7358, mientras que para la Fréchet (4,3), ese mismo valor tiene asociado un f(x)=0.0641. Se ha añadido, otra vez, un parámetro de localización. Comparando con la distribución anterior, si se evalúa la función de densidad para x=3, que corresponde a desplazar x=2 una unidad hacia la derecha, el valor de la función de densidad es el mismo en ese punto, f(x)=0.0641. El último gráfico corresponde a una Fréchet(5,1). 3.7.2. Distribución de Gumbel. 3.7.2.1. Características. Fue descubierta por Emil Julius Gambel, matemático judío nacido en Alemania a finales del siglo XIX. Es un caso particular de la distribución de valores extremos generalizada, y también es conocida como la distribución log-Weibull, o como la distribución exponencial doble. Según Reiss y Thomas (1997), la distribución de Gumbel tiene la misma importancia que la distribución Normal en otras aplicaciones. La función de distribución de la distribución de Gumbel es 38 mientras que la función de densidad viene dada por La distribución de Gumbel corresponde al caso en el que y En ese caso, la función de distribución viene dada por mientras que la función de densidad de probabilidad sería Media Varianza Mediana Moda Coeficiente de Asimetría Coeficiente de Curtosis Función Generatriz de Momentos Función Característica Dada una variable aleatoria U con distribución uniforme en el intervalo , entonces la variable sigue una distribución de Gumbel de parámetros y Ejemplo 9: Sea Si se tiene entonces Otra distribución relacionada con la de Gumbel es la Gompertz. Cuando la función de distribución de Y es la inversa de la distribución de distribución de la distribución de Gumbel estándar, entonces Y tiene una distribución de Gumbel. 3.7.2.2. Representaciones gráficas. A continuación se van a representar funciones de densidad y de distribución teóricas de la distribución de Gumbel. Se representarán tanto para el máximo como para el mínimo, comenzando para el máximo: 39 En primer lugar se ha representado la distribución de Gumbel para el máximo con valor del parámetro de localización igual a 0, y con parámetro de escala igual a 1. Se trata de la distribución de Gumbel estándar, y como se puede ver es algo asimétrica positiva. Por otra parte, la función de distribución comienza a crecer más significativamente después de x = -2. Seguidamente, la distribución que se representa tiene parámetro de localización igual a 3 y de escala igual a 1.5. El valor al que corresponde el pico más alto de la función de densidad es x = 3, cosa lógica si se tiene en cuenta que la moda de una distribución de Gumbel coincide con su parámetro de localización. Respecto a la distribución anterior, se ha cambiado el parámetro de localización, que ha pasado a ser 4 cuando antes era 3, luego la distribución se puede ver que se “mueve” una unidad hacia la derecha. 40 Conforme se hace mayor el parámetro de localización (ahora vale 5), el gráfico de la distribución se mueve más a la derecha. Ahora el parámetro de localización vale 3, y el de escala 2; con lo cual, si se compara con la distribución anterior, el gráfico se “traslada” hacia la izquierda, mientras que la escala cambia siendo el gráfico de la distribución algo menos leptocúrtica. En este caso se mantiene el parámetro de localización anterior, pero el de escala es más grande, pues vale 2.5; la moda sigue siendo 3, pero ahora f(3) vale menos que para la densidad anterior, pues la distribución ahora es más “aplastada”. 41 Por último, se representa la densidad y la función de distribución de una variable con distribución de Gumbel para el máximo con parámetros y la moda vale 4, y a su alrededor es donde se concentra mayor probabilidad. El que en todos los ejemplos vistos la variable sea asimétrica positiva no es casualidad, ya que al ser el coeficiente de asimetría para una variable con distribución de Gumbel para el máximo siempre positivo, cualquier variable con esa distribución será asimétrica positiva, independientemente de cuáles sean los valores de los parámetros. 3.7.2.3. Distribución de Gumbel para el mínimo. También existe la distribución de Gumbel para el mínimo, cuya función de distribución viene dada por mientras que la función de densidad es Algunas representaciones para este caso particular son: 42 Se puede ver un cambio bastante evidente respecto a los gráficos vistos antes para la distribución de Gumbel para el máximo; ahora, las colas se concentran a la izquierda en la función de densidad, con lo que la distribución es asimétrica negativa. Igualmente, se puede ver que ahora la moda es 0, que coincide con el parámetro de localización como viene siendo habitual (el de escala vale 0.5), y también se puede observar que el mayor crecimiento de la función de distribución se produce a partir de Ahora se ha cambiado el parámetro de localización, y como viene ocurriendo con los gráficos de variables aleatorias relacionadas con valores extremos, la distribución se “traslada”; en este caso se mueve una unidad hacia la derecha, pues el parámetro de escala sigue siendo el mismo. Por último, se ha representado la distribución de Gumbel estándar para el mínimo, esto es, al igual que en el caso del máximo, con parámetro de localización igual a 0 y de escala igual a 1. Como en los dos casos anteriores, la cola está concentrada a la izquierda; la explicación de esto es que, opuesto al caso del máximo, para la distribución de Gumbel para el mínimo la densidad es asimétrica negativa, independientemente de los valores de los parámetros. 3.7.3. Distribución de Weibull. 3.7.3.1. Características. Recibe su nombre del matemático sueco Waloddi Weibull, que la describió detalladamente en 1951, aunque fue descubierta inicialmente por Fréchet (1927) y aplicada por primera vez por Rosin y Rammler (1933) para describir la distribución de los tamaños en determinadas partículas. 43 La función de densidad de una variable con esta distribución es la siguiente: si . k es el parámetro de forma y es el parámetro de escala de la distribución. Su función de distribución de probabilidad viene dada por si Momento n-ésimo Media Varianza Mediana Moda si Coeficiente de Asimetría Coeficiente de Curtosis. donde Función Generatriz de momentos del logaritmo. Función Característica del logaritmo. También existe la distribución de Weibull con tres parámetros (se le añade el parámetro de localización , cuya función de densidad de probabilidad viene dada a continuación: , para 3.7.3.2. Representaciones gráficas. A continuación se representan la función de densidad y de distribución de la Weibull para distintos valores de sus parámetros; también se incluyen casos en los que se tienen tres parámetros: 44 La primera distribución representada es la que tiene como parámetro de forma igual a 2 y de escala igual a 1; al no haber parámetro de localización, este se supone igual a 0, con lo cual la densidad y la distribución existen para valores mayores que ese valor. A la vista de la gráfica de la función de densidad, se puede deducir que en este caso la distribución es asimétrica positiva, mientras que de la representación de la función de distribución se puede deducir que el crecimiento suele ser constante hasta que x= 1.5, a partir de donde empieza a decaer ligeramente para crecer cada vez menos. Ahora se cambia el parámetro de escala, que es mayor, luego cambia la escala de la distribución; a la vista de la representación de la función de densidad se ve que pasa a estar más “aplastada”, pero a la vez es más “ancha”. 45 En este caso, el parámetro de forma vale 2.5, mientras que el de escala es igual a 1. La distribución es asimétrica positiva al estar la cola a la derecha y los valores con mayor probabilidad más a la izquierda. Ahora se vuelve a cambiar el parámetro de escala, que vale ahora 1.5; mientras que el de forma sigue siendo 2.5, con lo cual no varía la forma de la distribución. Como ocurre con los cambios de escala cuando el parámetro pasa a ser mayor, la distribución se “aplasta más” pero abarca más valores con probabilidad significativa. Ahora se ha añadido un parámetro de localización, representaciones son para valores superiores a 3. con lo cual ahora las La siguiente distribución representada es una Weibull con parámetro de forma igual a 3 y de escala igual a 1; esta parece más centrada, y su forma se parece a la de la Normal. 46 En la última representación, el parámetro de escala se ha ampliado a 2; se aprecia un cambio evidente en la escala de los datos; mientras que la forma sigue siendo la misma, la distribución es bastante simétrica. 3.8. Niveles de retorno. Estudio gráfico de la bondad del ajuste. Otra definición importante es la de los niveles de retorno, que en algunos campos como la hidrología o la climatología tienen mucha importancia. Son considerados como los cuantiles de la distribución de valores extremos. Así, si (el nivel de retorno) es el cuantil de orden p de una variable con distribución GEV, entonces p es la probabilidad de que sea superado una vez al año; y el período de retorno, , es el número de unidades de tiempo que transcurrirán en media entre dos veces en los que la variable supere el valor de Ejemplo 4: si se tiene un período de retorno de 50 años, eso equivale a una probabilidad anual de 0.02; y si el periodo de retorno es de 10 años, la probabilidad correspondiente sería de 0.10. Relacionados con los niveles de retorno, existen los gráficos de nivel de retorno, en los cuales se representan los niveles de retorno estimados y sus periodos de retorno asociados en una escala logarítmica, ya que según Ketchen y Ver (2006) así la cola de la distribución está comprimida, con lo cual las estimaciones de niveles de retorno para períodos de retorno largos se pueden visualizar en el gráfico. Otros gráficos de diagnóstico usados para comprobar como de buenos son los modelos de valores extremos son el gráfico P-P, el gráfico Q-Q y el gráfico de densidad. Sea Gráfico P-P: una muestra de una población con función de distribución estimada Entonces, se representa el gráfico de dispersión de los puntos , gráfico que recibe el nombre de gráfico P-P. Si el modelo se ajusta bien a los datos, entonces los puntos en el gráfico formarán una recta cuyo ángulo sea bastante cercano a los 45 grados. Gráficos Q-Q: Sea una estimación de la función de distribución F basada en una muestra de una población con función de distribución estimada. Entonces, el gráfico de dispersión de los puntos i = 1, 2, …, n recibe el nombre de gráfico Q-Q. Al igual que en el 47 gráfico P-P, si el modelo se ajusta bien a los datos, entonces los puntos en el gráfico formarán una recta cuyo ángulo sea bastante cercano a los 45 grados. Otro gráfico que se suele utilizar para comprobar visualmente cómo de bueno es el modelo de valores extremos es el gráfico de densidad, que representa los valores junto a un histograma y la densidad teórica de la distribución. Más adelante se verán ejemplos en los que se usan dichos gráficos para comprobar gráficamente la bondad del ajuste. 3.9. Estimación de los parámetros por Máxima Verosimilitud. Al ser los parámetros desconocidos, hay que estimarlos; según Coles (2004), existen muchas técnicas distintas para hacer dichas estimaciones, pero la preferible es la estimación por máxima verosimilitud. No es la técnica perfecta, ya que para algunos casos concretos los estimadores obtenidos no se comportan adecuadamente, pero sí es la más útil para este caso concreto. La estimación se hace por bloques, y lo que se quiere maximizar es la siguiente función (logaritmo de la verosimilitud): con la condición de que para Mientras que en el caso de que la función a maximizar es la siguiente: No es posible lograr una solución analítica para ninguna de las ecuaciones, pero si se tienen unos datos concretos, se pueden resolver usando algoritmos de optimización numéricos estándar. Más adelante, en este trabajo se verán con el paquete R estimaciones de los parámetros por máxima verosimilitud dados conjuntos de datos concretos. 3.10. Ejemplos con bloques y con análisis gráficos. Ejemplo 10: A continuación se va a trabajar con unos datos a los cuales se les va a aplicar un modelo de valores extremos. Los datos (Hipel and Mcleod, 1994) corresponden al desempleo anual en los Estados Unidos desde 1890 hasta 1970. Lo primero que se hace es cargar el fichero con los datos. Luego, se crea un data.frame con los años y los valores para cada año. 48 Los valores junto con el año al que corresponden y su número de observación se pueden ver a continuación: Mientras que la representación gráfica de los datos es la siguiente: 49 A la vista del gráfico de los datos, se puede ver que los valores más grandes se dan entre 1930 y 1940. A continuación se va a ajustar un modelo GEV para los datos, para lo cual hay que cargar el paquete extRemes. Una vez dentro de él, se leen los datos y se le pide que ajuste los datos a una distribución de valores extremos generalizada 50 Como se puede ver, el vector de parámetros estimado es: mientras que la matriz de varianzas-covarianza es El valor del estadístico usado para el test de razón de verosimilitudes es 20.19778, claramente mayor que el valor crítico de una Chi-Cuadrado con un grado de libertad. A continuación se pueden ver el gráfico probabilístico, el gráfico de cuantiles, el gráfico de niveles de retorno y el gráfico de densidad: 51 A la vista de estos gráficos, el ajuste no parece malo, pues los datos están más o menos dispuestos sobre la línea recta del gráfico probabilístico y el de cuantiles. En el gráfico de niveles de retorno, se puede ver sin más que extrapolar que aproximadamente un nivel de retorno igual a 30 corresponde a un período de retorno cercano a los 100 años. Para terminar, se muestra el gráfico de la vida media residual: 52 Seguidamente se tiene con ejemplo: Ejemplo 11: Se tienen datos correspondientes a las inundaciones en el “Río de las Plumas” (Feather River), situado en California. Los datos van de 1902 a 1960, y están expresados en pies cúbicos por segundo. *Fuentes: (Benjamin, J.R. y Cornell, C.A. (1970). Probability, Statistics and Decicions for Civil Engineers. McGraw-Hill, New York; y Pericchi, L.R. and Rodriguez-Iturbe, I. (1985). On the statistical analysis of floods. En: A Celebration of Statistics. The ISI Centenary Volume, A.C. Atkinson y S.E. Fienberg (eds.), 511-541.) Se leen primero los datos. A continuación se muestran junto con el año al que corresponden: 53 El ajuste que se ha hecho es el siguiente: 54 Se destaca el valor del estadístico del test del cociente de verosimilitud, es 2.725639, que es menor que el valor crítico de una chi-cuadrado con 1 grado de libertad (cuando se toma un nivel de significación del 5%); el p-valor es 0.0987, y las estimaciones de los parámetros por máxima verosimilitud serían las siguientes: . 55 A la vista del gráfico probabilístico y el de cuantiles, los datos están cercanos a formar una línea recta, así que el ajuste parece adecuado. A continuación se va a ajustar un modelo de la distribución GEV para cada uno de los bloques vistos en el ejemplo anterior; en esta ocasión, en vez de usar el menú de extRemes, se usará la sentencia “gev.fit” que viene incluida en el paquete ISMEV: 56 “conv” corresponde al código de convergencia. Si vale 0 significa que hay convergencia, como es el caso de este primer bloque. “nllh” muestra el valor del logaritmo negativo de la verosimilitud evaluado en los estimadores de máxima verosimilitud. En este caso vale 139.5141. “mle” muestra el valor de los estimadores de máxima verosimilitud de los parámetros. La estimación del parámetro de localización es 395112.9; del parámetro de escala 24147.69, y del de forma, -0.12526. La razón de valores tan grandes es que al estar los datos divididos por bloques, y ser en este caso los bloques de 12 datos, el número de datos no es demasiado elevado, con lo cual se obtienen esas estimaciones con sesgos también altos. En este caso, la desviación estándar del estimador del primer parámetro es 22709.13; del segundo, 18259.47, y del tercero, 0.7003. Para el segundo bloque que se ha formado hay convergencia a la hora de estimar; el logaritmo negativo de la verosimilitud evaluado en las estimaciones vale 138.3817, los valores estimados de los parámetros son y los correspondientes errores estándar valen . Para el tercer bloque que se ha formado hay convergencia a la hora de estimar; el logaritmo negativo de la verosimilitud evaluado en las estimaciones vale 138.5130, los tres valores estimados de los parámetros son y los correspondientes errores estándar valen . 57 Para el cuarto bloque hay convergencia a la hora de estimar; el logaritmo negativo de la verosimilitud evaluado en las estimaciones vale 145.6419, los valores estimados de los parámetros son y los errores estándar valen ; para aparece un “NaN” (Not a Number), posiblemente por haber tenido que dividir entre 0. Para el bloque número 5 también hay convergencia; el logaritmo negativo de la verosimilitud evaluado en las estimaciones tiene el valor de 141.5824, y los estimaciones de máxima verosimilitud son Como se puede ver, para los errores estándar, aparece un “NaN” para cada parámetro. Para el sexto bloque que se ha formado hay convergencia a la hora de estimar; el logaritmo negativo de la verosimilitud evaluado en las estimaciones vale 146.7671, los valores estimados 58 de los parámetros son y los correspondientes errores estándar valen . Para el bloque número 7, igual que para los seis anteriores, también hay convergencia; el logaritmo negativo de la verosimilitud evaluado en las estimaciones tiene el valor de 145.3059; y los estimaciones de máxima verosimilitud son Como se puede ver, para los errores estándar aparece un “NaN” para cada parámetro. Para el bloque 8 hay convergencia a la hora de estimar; el logaritmo negativo de la verosimilitud evaluado en los estimaciones vale 140.4077 , las estimaciones de los parámetros son y los correspondientes errores estándar valen . 59 Por su parte, para el bloque 9 se tiene lo siguiente: hay convergencia también; el valor del logaritmo negativo de la verosimilitud evaluado en las estimaciones es 144.473. Los valores estimados de los parámetros son y los correspondientes errores estándar valen . Para el bloque 10 se tiene que hay convergencia también; el valor del logaritmo negativo de la verosimilitud evaluado en los estimaciones es 148.0332. Los valores estimados de los parámetros son y los correspondientes errores estándar valen . Con el siguiente bloque, el 11, igualmente hay convergencia. El valor del logaritmo negativo de la verosimilitud evaluado en los estimaciones es 145.0853. Los valores estimados de los parámetros son y los errores estándar para los parámetros de escala y de forma valen . Para el parámetro de localización no se obtiene. 60 Para el bloque 12 se tiene que hay convergencia también; el valor del logaritmo negativo de la verosimilitud evaluado en las estimaciones es 143.9937. Los valores estimados de los parámetros son y los errores estándar asociados valen . Con el siguiente bloque, el 13, al igual que con los doce anteriores, también hay convergencia. El valor del logaritmo negativo de la verosimilitud evaluado en las estimaciones es 143.621. Los valores estimados de los parámetros son y los errores estándar para los parámetros de escala y de forma valen . Para el parámetro de localización no se obtiene valor del error estándar. Para el último bloque también hay convergencia; el logaritmo negativo de la verosimilitud evaluado en las estimaciones vale 139.2543. Los valores estimados de los parámetros son 61 y los errores estándar asociados valen . En el caso del penúltimo bloque se da asimismo la convergencia, el valor del logaritmo negativo de la verosimilitud evaluado en los estimaciones vale 142.731. El vector con las estimaciones es El valor del error estándar del estimador sólo aparece para y es igual a 0.2883. Por último, en el bloque 16 también se cumple la convergencia, con la cual la hay en todos los bloques. El vector con las estimaciones es y Los errores estándar valen ; para aparece un “NaN” (Not a Number). 62 CAPÍTULO 4: MODELOS DE UMBRALES. 4.1. Excedencias. Los autores suelen dar bastante importancia a los modelos de umbrales dentro de la teoría de valores extremos. En algunos casos, es mejor usar modelos de umbrales para estudiar valores extremos, antes que usar la distribución GEV. En este contexto, se parte de unos datos originales Entonces a los valores si superaciones del umbral. y se fija un umbral u. se les llama excedencias o Una definición más formal de las excedencias es la siguiente: -Definición 1: Sea que el suceso una variable aleatoria unidimensional, y sea u un umbral fijado. Se dice es una excedencia del umbral u, si se cumple que Ejemplo 1: Un dique rompeolas se puede destrozar cuando las olas por ejemplo alcanzan una altura de 10 metros, 1 con lo cual no importa si la altura de la ola es de 10.1, 11.5 ó 25 metros pues en cualquier caso el rompeolas será destrozado. Ejemplo 2: Este ejemplo está relacionado con el llamado “límite elástico”. Normalmente, los puentes colgantes están sujetos por cables largos, pero en algunos laboratorios se experimenta con cables más cortos que son mucho más resistentes que los largos, lo cual se explica por el “principio del eslabón más débil”, según el cual la fuerza de una pieza larga es la mínima fuerza de todas las piezas que la forman. Por lo tanto, el ingeniero que realiza el estudio en el laboratorio, tiene que extrapolar sus resultados teóricos a cables reales. En este caso, el diseño de un puente colgante requiere que se sepa cuál es la probabilidad de que la resistencia del cable esté por debajo de ciertos valores, así que por esa razón en este ejemplo los valores debajo de un umbral son importantes. Ejemplo 3: Se considera una muestra de 10 valores generados según una Poisson de parámetro 10, y se considera el umbral u=40. Dichos valores (generados con R) son los siguientes: Para ver las excedencias, hay que restar a los valores de la muestra el umbral, y luego ver cuáles de estos valores son positivos: Como se puede ver, resultan sólo dos valores positivos, luego sólo dos valores de la muestra son mayores que el umbral establecido. Si se consideran como valores extremos a los que cumplen esa condición, ser mayor que el umbral, entonces los dos únicos valores extremos de la muestra serían la octava y novena observación. 63 Los datos representados junto al umbral (dibujado mediante una línea horizontal) se pueden ver a continuación: Ejemplo 4: Se tienen los datos reales (Hipel and Mcleod, 1994) que corresponden al número de nacimientos por cada 10.000 de mujeres de 23 años en los Estados Unidos desde 1917 a 1975. Como es habitual con este tipo de ejemplos, primero se leen los datos externamente y luego se asignan a un “data.frame”: Los datos son los siguientes: 64 Mientras que los datos representados junto al umbral que se selecciona a priori son los siguientes: 65 Como se puede ver, son siete los valores mayores que el umbral, por lo que si se consideran como valores extremos aquellos mayores que el umbral dado, dichos valores serán valores extremos para estos datos. En concreto, los valores mayores que el umbral son los siguientes: que son los años entre 1956 y 1962, ambos inclusive. También se puede ver cuáles son los valores extremos usando las excedencias: 66 La nueva columna, “exced”, sirve para obtener las excedencias del umbral calculando las diferencias de cada valor respecto al umbral, para luego saber qué valores son superiores a u y, por tanto, son excedencias: Como se puede ver, los años en los que el valor supera al umbral (que coinciden con los que la variable “exced” es mayor que 0) son los mismos que antes. La distribución de la excedencia del umbral u, partiendo de una variable aleatoria es : 67 Según Coles, para un umbral suficientemente grande se puede calcular dicha distribución, que aproximadamente sería definida para donde Dicha función de distribución corresponde a la de la familia de Pareto Generalizada, distribución que se estudiará más adelante en este trabajo. Así, las observaciones de las excedencias, se consideran realizaciones de una variable aleatoria con distribución aproximada de Pareto generalizada. Por otra parte, también es importante estudiar el número de veces que las observaciones son mayores que el umbral, esto es, el número de excedencias sobre u. Dadas las variables aleatorias idénticamente distribuidas, se define K como donde Entonces la distribución de K viene dada por que corresponde a la f.m.p. de una variable Binomial de parámetros n y p, donde , ya que es la probabilidad de que el valor sea superior al umbral. Con lo cual, el número medio de excedencias del umbral vendrá dado por Ejemplo 5: Sean variables idénticamente distribuidas según una Normal con media 45 y desviación típica 3. Se considera el umbral Se quiere calcular el número esperado de excedencias del umbral. Se tiene que y ahora se ha de calcular Se tiene que por lo que simplemente hay que calcular la probabilidad de que una Normal con media 45 y desviación estándar 3 sea menor o igual que 50. Dicha probabilidad, calculada en R, es: Por tanto, Con lo cual, se espera que el umbral sea superado en media veces, y redondeando, lo esperable es que de cada 10 veces sólo 1 se supere el umbral. Ejemplo 6: Se considera el ejemplo 1 visto anteriormente del rompeolas. En particular, se tiene un rompeolas cuya esperanza de vida es 60 años, y se supone que la probabilidad de que la ola supere la altura de 10 metros es 0.15, entonces la probabilidad de que haya 15 años en los que haya excedencias durante esos 60 años de vida viene dada por la probabilidad de que una Binomial con parámetros n = 60 y p = 0.10 tome el valor 15; esto es, 68 También, para un n suficientemente grande, se pueden aproximar las probabilidades anteriores de la Binomial mediante una Poisson. La Poisson aproximada tendría como parámetro Ejemplo 7: (Castillo, Hadi, Balakrishnan y Sarabia (2004)). Un ejemplo de la distribución de Poisson aplicada a valores extremos es el siguiente: Se supone que las tormentas con cierta intensidad ocurren en media cada 80 años en un determinado lugar, y se quiere calcular la probabilidad de que no haya una tormenta en un año determinado. Si se supone que la variable tiene una distribución de Poisson, su parámetro viene dado por 1\80=0.0125, así que la probabilidad que se quiere calcular es Por tanto, la probabilidad de que no haya tormenta en cierto año es 0.9876. Relacionados con el número de excedencias sobre el umbral, también algunos autores como Reiss y Thomas (1997) mencionan los tiempos de excedencias, esto es, en qué momentos el umbral es superado, algo que también es de interés. Si son las excedencias sobre el umbral u, entonces son los tiempos de excedencia ordenados. Si se tiene una sucesión infinita de variables aleatorias idénticamente distribuidas, y se tiene un umbral u, el primer tiempo de excedencia en ese umbral viene dado por , mientras que el segundo tiempo de excedencia es , de lo cual se deduce que para un r genérico, para Es también interesante estudiar la distribución de los tiempos de excedencia respecto a un umbral. Los tiempos de excedencia, son independientes entre sí (y consiguientemente, los periodos de retorno, , también) y están distribuidos según una variable geométrica de parámetro ya que se mide el número de intentos hasta el primer éxito (cuando el umbral es superado). Así, la probabilidad de que por ejemplo el primer tiempo de excedencia sea k suponiendo que las variables sean además independientes es la siguiente: siendo k un entero positivo. Por tanto, el tiempo esperado para que ocurra la primera excedencia viene dado por la esperanza de una variable geométrica de parámetro , esto es, Ejemplo 8: Se tiene el ejemplo anterior de las variables idénticamente distribuidas según una con umbral Se calculó antes que Entonces, la media del primer tiempo de excedencia viene dada por La probabilidad de que el primer tiempo de excedencia sea k sería la siguiente: 69 para k entero positivo. Para varios valores de k, la probabilidad asociada viene en la siguiente tabla: k PROBABILIDAD 1 0.10565 2 0.0945 3 0.0845 4 0.0756 5 0.0676 6 0.06045 7 0.0541 8 0.04835 9 0.0432 10 0.0387 Para terminar con esta parte, se va a estudiar un concepto similar al de niveles de retorno visto en el capítulo sobre la distribución GEV; dicho concepto es el de umbral de retorno, y viene dado por , que corresponde al umbral en el cual la media del tiempo de la primera excedencia es T. Es fácil ver que por lo que sin más que despejar, se obtiene que El umbral de retorno es superado con probabilidad por la observación en un periodo dado. 4.2. La Distribución de Pareto Generalizada. La distribución de Pareto Generalizada tiene una gran importancia en los modelos de umbrales en particular y en la teoría de valores extremos en general, ya que es la distribución límite de las excedencias de umbrales. Ahora se van a estudiar varias características de la distribución de Pareto Generalizada. Para comenzar, los parámetros de la distribución cuando ésta tiene tres parámetros son (parámetro de localización), (parámetro de escala) y (parámetro de forma). Su función de densidad viene dada por 70 ó para cuando y cuando mientras que la función de distribución es la siguiente: para cuando ,y cuando donde Algunas características de esta distribución son las siguientes: Media Varianza (siempre que (siempre que ) Mediana En el caso de que la distribución tenga dos parámetros (caso más común, corresponde a , su función de densidad viene dada por: mientras que la función de distribución es: El p-cuantil viene dado por: También existe la distribución Generalizada de Pareto para el mínimo, cuya función de densidad es 71 La función de distribución correspondiente es: que es la distribución límite de Y el cuantil de orden p viene dado por Para simular valores de una variable distribuida según una distribución de Pareto Generalizada con tres parámetros, se usa el siguiente resultado: si U es una variable con distribución Uniforme y definida en el intervalo entonces la siguiente variable sigue una distribución de Pareto Generalizada con parámetros La d¡Distribución de Pareto Generalizada para el máximo con parámetros ( siguientes casos particulares: tiene los Cuando la distribución de Pareto Generalizada con dos parámetros para el máximo es la distribución exponencial con media Cuando la distribución de Pareto Generalizada con dos parámetros para el máximo es la distribución uniforme de parámetros 0 y Mientras que esa distribución para el mínimo y también con parámetros particulares análogos: y y tiene casos Cuando la distribución de Pareto generalizada con dos parámetros para el mínimo es la distribución exponencial inversa con media Cuando la distribución de Pareto generalizada con dos parámetros para el mínimo es la distribución uniforme de parámetros – y 0. La distribución generalizada de Pareto para el máximo y su caso análogo para el mínimo están relacionadas de una forma bastante similar al caso de la distribución GEV para el mínimo y para el máximo. Si donde es la distribución generalizada de Pareto para el máximo, entonces siendo la distribución generalizada de Pareto para el mínimo. Igualmente, 72 Aunque en este trabajo lo que se hará será simular valores de esta distribución usando el paquete extRemes; con dicho programa sólo hay que introducir los parámetros de escala y de forma y el umbral para simular los datos. A continuación, y como se hizo en el tema anterior de este trabajo con la distribución de valores extremos generalizada, se van a simular valores de variables con distribución de Pareto Generalizada usando R. 4.3. Ejemplos. 4.3.1. Datos simulados. Para empezar, se comienza simulando datos de una variable GP(5, 0.6). El umbral se pone como 0, el número de datos que se van a simular es 50 y los datos se guardan como “datos1”: La representación gráfica de los datos es la siguiente: 73 (Se puede ver que todos los datos generados son superiores al umbral establecido). A continuación se van a generar datos también de una GP(5, 0.6), pero ahora el umbral se va a aumentar y va a pasar a ser 10. Los datos se almacenan como “datos2”: 74 (Al igual que para los datos anteriores, todos los valores son superiores a 10, que es el umbral). Ahora se va a generar una GP(7, 0.3), siendo el umbral 5. Los 50 valores simulados (“datos3”) son los siguientes: El gráfico de los datos se puede ver a continuación. 75 (También los 50 valores generados son mayores que el umbral, 5). Ahora se cambia el parámetro de forma, con lo cual la distribución que se simula es una GP(7, 0.9), con umbral igual a 5. Los datos (“datos4”) son los siguientes: Y la representación gráfica de los datos es: 76 Al igual que para los otros datos, los valores son todos superiores al umbral, pero se puede apreciar claramente que la forma de la distribución de los valores ha cambiado. Por último, se va a probar a cambiar el parámetro de escala, así que primero se van a generar 50 valores de una GP(10, 0.2), con umbral 15. Dichos datos (“datos5”) son los siguientes: La representación gráfica de estos datos se puede ver a continuación: 77 (Como viene siendo habitual, todos los valores simulados son mayores que el umbral). Ahora se va a simular una GP(20, 0.2) con umbral 15, se ha cambiado en esta ocasión el parámetro de escala. Los datos generados (“datos6”) son los que vienen a continuación: Y su representación gráfica: 78 Se puede apreciar un cambio en la escala de variación de los datos. 4.3.2 Representación de distribuciones de Pareto generalizadas teóricas. En este apartado se van a representar varias distribuciones teóricas de la distribución de Pareto generalizada. Al igual que con las representaciones para la distribución GEV, para el programa EasyFit, si bien para la Pareto Generalizada se incluyen los mismos parámetros, estos aparecen en otro orden: primero el de forma, segundo el de escala y tercero el de localización: La primera distribución representada es una GP(0, 1, -3), o una GP(1, -3) con dos parámetros. Como se puede ver, la cola de la distribución está a la izquierda, y partir del valor comienza un crecimiento significativo. 79 Ahora se cambia el parámetro de forma, y la distribución representada tiene parámetro de escala también igual a 1, pero de escala igual a -0.7. A la vista de los gráficos de la función de densidad y de distribución se observa un cambio bastante evidente en la representación. En este caso también se mantienen los parámetros de localización y de escala, pero el de forma ahora es positivo; al contrario que en el primer ejemplo, ahora las colas están a la derecha, y el crecimiento va disminuyendo conforme aumentan los valores de x. La forma de la función de distribución también es bastante distinta pues el mayor crecimiento ahora es al principio. Lo que se cambia ahora es el valor del parámetro de escala, que es 1.25 (se tiene una GP(1.25, 3)); se puede apreciar el cambio en la escala pues ahora la representación está más “aplastada” y con una cola que abarca más. 80 Esta representación es análoga a la anterior, simplemente el parámetro de escala sigue aumentando y pasa a ser 1.75. Como es lógico, la cola se ensancha más. La distribución que se tiene ahora es una GP(1, 3, 3), respecto a la anterior se ha cambiado el parámetro de localización y el de escala; sobre todo se destaca el cambio del parámetro de localización, pues ahora la densidad y la distribución están representadas para valores superiores a 1. Por último, se representa una GP(2.5, 1, 3). La distribución no es nula para valores mayores que 2.5, la cola está concentrada a la derecha con lo cual los valores más probables están a la izquierda (a la derecha de , y el mayor crecimiento de la función de distribución, como es esperable, es para también los valores más cercanos a la izquierda. 4.3.3. Ejemplos con datos reales. 81 A continuación se van a usar ejemplos prácticos de modelos de umbrales con datos reales. Ejemplo 9: El primer ejemplo, corresponde a la temperatura corporal en grados Celsius medida a una mujer por la mañana durante 60 días seguidos (la fuente exacta de los datos es desconocida, pero están sacados de la página http://robjhyndman.com/TSDL/health/), y son unos datos útiles para esta parte del trabajo pues justamente la temperatura corporal es un muy buen ejemplo del uso de umbrales; se dice que una persona tiene fiebre cuando su temperatura es mayor que 37º C, con lo cual se puede considerar el umbral como 37, con lo cual habría excedencias siempre que se rebasase dicha temperatura. Primero de todo, se leen en R los datos externos: A continuación, se pueden ver los 60 datos: Y la representación gráfica de los datos se puede visualizar a continuación: 82 A continuación, se va a intentar ajustar una distribución de Pareto generalizada a los datos usando el paquete extRemes. Como umbral, se introducirá 37, y el número de observaciones anuales coincidirá con el número de observaciones que hay en los datos, pues todas las observaciones son en 60 días seguidos. El estadístico del cociente de verosimilitud es relativamente grande, 154.2240, que es superior al valor crítico de la chi-cuadrado con 1 grado de libertad, con lo cual el p-valor es bastante pequeño. Se puede ver que hay un total de 6 excedencias, y que el valor estimado del parámetro de escala es 1.5047, mientras que el del parámetro de forma es -1.6719. La representación de la distribución teórica con esos parámetros es la siguiente: Los gráficos probabilístico, de cuantiles y de niveles de retorno parecen además que el ajuste no es bueno: 83 El gráfico de densidad no aparece, como se puede ver, presumiblemente por la escasez de excedencias. Ejemplo 10: Se van a intentar ajustar otros datos (Shumway y Stoffer, 2000) correspondientes al espesor de 634 varvas glaciares en el estado norteamericano de Massachusetts. Dichos datos son los siguientes: 84 85 Un resumen estadístico inicial de los datos se puede ver a continuación: 86 La representación gráfica de los datos es la siguiente: Al contrario que en el ejemplo anterior, esta vez no hay un umbral “predeterminado”, con lo cual habrá que buscar alguna forma de seleccionar un umbral. Una buena opción es usar el gráfico de la vida media residual, que puede servir para ver cual umbral es mejor en función de la representación gráfica. 87 Se va a seleccionar un umbral u = 75, pues a partir de ese valor aproximadamente se aprecia un cambio significativo en el que el gráfico comienza a ser lineal (localmente). Así que en principio se va a seleccionar dicho umbral. El análisis es el siguiente: El valor del estadístico del test de la razón de verosimilitudes es 5.1454, que es mayor que el valor crítico de una chi-cuadrado con 1 grado de libertad, que es 3.841459, mientras que el pvalor es 0.0233. En total hay 29 excedencias de umbral, y el vector de parámetros estimado es el siguiente: Los errores estándar estimados son 3.0616 y 0.3421, respectivamente,mientras que la matriz estimada de covarianzas es la siguiente: Y para terminar con este ejemplo, se tienen el gráfico probabilístico, el gráfico de cuantiles, el gráfico de niveles de retorno y el gráfico de densidad: 88 Para este ejemplo sí se puede ver el gráfico de densidad. En los gráfico probabilístico y de cuantiles, los datos están más o menos en línea recta (sobre todo en el primer gráfico), aunque se observan ciertas desviaciones. Ahora se va a cambiar el umbral, para probar si el ajuste realizado es peor o mejor que el anterior. El nuevo umbral, también en una zona cercana al anterior donde empieza a haber linealidad, ahora es u = 85. Primero de todo, se ve que el valor del estadístico del test de la razón de verosimilitudes es bastante más pequeño, 0.1757, con lo cual se sugiere que este modelo sí es más adecuado para los datos que el anterior. Ahora el número de excedencias es menor, 13 en concreto. 89 El vector de parámetros estimado es el siguiente: Los errores estándar estimados son 10.2617 y 0.4992, respectivamente; mientras que la matriz estimada de covarianzas es la siguiente: Por último, se muestran los gráficos para visualizar el ajuste del modelo: Al igual que en el caso anterior, los datos están más o menos en línea recta (sobre todo el gráfico probabilístico), pero no demasiado clara, aunque se observan ciertas desviaciones. 90 CAPÍTULO 5: OTROS ASPECTOS. En este último capítulo se tratan otros aspectos relacionados con la teoría de valores extremos que, si bien no pretenden en este trabajo darles un desarrollo tan extenso como el de los dos capítulos anteriores, si merecen que se les mencione brevemente. 5.1. Valores extremos en Series Estacionarias. Intuitivamente, una serie temporal se considera estacionaria si sus propiedades estadísticas (media, varianza…) son constantes a lo largo del tiempo. Otra definición algo más concreta es la siguiente: una proceso (o serie) estacionario es aquel en el que las distribuciones de probabilidad se mantienen estables a lo largo del tiempo; esto es, que la distribución de un conjunto de variables se mantiene igual aunque dichas variables se desplacen h unidades. Esta misma definición, se puede expresar de una manera más formal de la siguiente forma: -Definición 1: Sea una serie temporal. Se dice que dicha serie es estacionaria si para cada conjunto de índices temporales la distribución conjunta de coincide con la distribución conjunta de Según Beirlant, Segers, De Waal y Ferro, estudiando series temporales dependientes, se tiene que la dependencia afecta al comportamiento cualitativo de los valores extremos; con lo cual se necesitan nuevos métodos y herramientas para abarcar este tipo de estudio de valores extremos. Existen dos formas de analizar valores extremos en una serie temporal; la primera consiste en elegir un modelo para los valores extremos del proceso, y ajustarlo a los valores extremos de los datos. La segunda parece más difícil, porque trata de elegir un modelo de serie temporal para el proceso completo, ajustarlo a los datos y luego intentar estudiar el comportamiento de los valores extremos de dicho proceso. Se tiene la siguiente definición de la que hacen mención varios autores: -Definición 2: Una serie estacionaria si, para todo donde para alguna sucesión se dice que satisface la condición de los con entonces de forma que cuando Según Coles, esa condición asegura que, para grupos de variables que están suficientemente lejanas, la diferencia en probabilidades anterior (mientras no sea 0) es suficientemente cercana a cero para no tener efecto en las leyes de límites para extremos. Se tiene el siguiente teorema, de Leadbetter: -Teorema 1: Sea un proceso estacionario y defínase si y son sucesiones de constantes de forma que Entonces 91 cuando donde G es una función de distribución no degenerada, y la condición de los se cumple para para cada real z, entonces G pertenece a la familia de distribuciones de valores extremos generalizada. 5.2. Valores Extremos en Series no estacionarias. Al contrario que en los procesos estacionarios, las características de las series temporales no estacionarias cambian con cierta frecuencia a lo largo del tiempo. La no estacionariedad se puede expresar a través de cambios en los parámetros del modelo; por ejemplo, se puede expresar el parámetro de localización como un polinomio de tercer grado: O como una función lineal sin termino constante: Con lo cual el modelo que se tiene para la serie temporal no estacionaria es: Que desglosando más, sería una para el primer caso, y una para el segundo. También se puede expresar la no estacionariedad en el parámetro de escala: Pero para el parámetro de forma, es menos bueno expresarlo también en función de tiempo ya que los parámetros de forma son difíciles de estimar con precisión. Aún así, un modelo con todos sus parámetros expresados en función del tiempo sería: Al igual que con el modelo GEV “estándar”, y con los modelos de umbrales, también se pueden hacer estimaciones por máxima verosimilitud, o mediciones de la bondad del ajuste del modelo. 5.3. Caso de variables no independientes ni idénticamente distribuidas. Éste es otro caso que mencionan algunos autores y que es interesante tratar. Aquí se parte de las variables aleatorias , donde cada una tiene su distribución marginal, y donde además esta vez no se supone que las variables sean independientes entre sí. Este tipo de variables se usan en campos donde existe una relación de dependencia, tales como ecología o meteorología. 92 Según Falk, Hüsler y Reiss (2010), para tratar los valores extremos de este tipo de secuencias, se necesita una teoría más general para valores extremos, pues la teoría clásica está bastante limitada para las series no independientes ni idénticamente distribuidas. El caso de las variables no independientes ni idénticamente distribuidas se puede generalizar de varias maneras mediante la no suposición de independencia o no suponiendo la idéntica distribución de las variables Según los autores anteriores, se ve que en el caso estacionario o en el que existe sólo independencia, el comportamiento de los valores extremos y sus excedencias de un nivel u puede ser bastante distinto al caso de las variables independientes e idénticamente distribuidas. 5.4. Caso Multivariante. Según Kotz y Nadarahaj (2001), la teoría que trata los valores extremos multivariantes, pese a ser bastante nueva, se ha convertido en un campo en el cual se ha avanzado bastante. Un ejemplo en el que se puede utilizar la teoría de valores extremos multivariante está relacionado con Internet; concretamente con datos de tráfico en Internet, ya que su distribución se comporta como una variable con cola pesada. En este ejemplo (Maulik Et. Al, 2002), la teoría de valores extremos multivariante puede usarse en varias de las variables usadas, como son el tamaño del archivo transferido, la tasa media de “thoughput” (término usado para denotar el volumen de información que fluye a través de un sistema) y la cantidad de tiempo que se toma para transferir el archivo. El desarrollo multivariante es análogo al univariante; si se tienen los vectores aleatorios e idénticamente distribuidos con función de distribución conjunta F, el máximo se obtendrá componente a componente. Así, por lo que ya que se cumple que si y sólo si, Para definir los máximos multivariantes, se calculan los extremos componente a componente. Al igual que en el caso unidimensional, la función de distribución se puede sustituir por una distribución límite: para vectores y Si se cumple para elecciones adecuadas de Multivariante de Valores Extremos. y entonces G es una Distribución Según Coles, un problema que tienen los procesos multivariantes es que en niveles altos la dependencia suele estabilizarse, de tal modo que los sucesos más extremos están más cercanos a la independencia, por lo cual, según dicho autor, el aplicar métodos tradicionales a procesos de ese tipo puede conducir a resultados engañosos. 93 5.5. Extremos espaciales. Existen casos en los que interesa tratar con valores extremos en un contexto espacio-temporal, pues aparte de los valores de la variable correspondiente en el tiempo, se tiene una localización. Algunos ejemplos de este tipo de extremos son avalanchas, olas de calor, etc. Si las localizaciones están indexadas, se puede definir como el valor de la variable en una localización Se trata de trabajar con el (y en su caso con esto es, con el máximo (y mínimo) de variables espaciales. Al igual que en el caso no-espacial, existe un análogo de las series máximo y mínimo estables (los procesos espaciales máximo y mínimo estables). Cuando se pretende modelizar procesos espaciales, la metodología usada es análoga a la usada anteriormente con el teorema de valores extremos. 5.6. Teoría bayesiana aplicada a valores extremos. La teoría bayesiana también tiene aplicación dentro de los valores extremos. Es más, es bastante importante porque en muchas ocasiones es preferible su uso a otros métodos clásicos de estimación de valores extremos tales como la máxima verosimilitud. Coles afirma que es bueno incluir análisis bayesianos de valores extremos pues al ser los datos extremos escasos, el usar una distribución a priori puede ser útil para tener más información; y sobre todo porque la inferencia bayesiana proporciona un análisis más completo que la inferencia por máxima verosimilitud, porque además esa inferencia no depende de hipótesis, al contrario que en el caso de máxima verosimilitud, que sí las requiere. Así, se puede estimar la probabilidad de que un suceso futuro alcance un nivel extremo a través de la distribución predictiva, que tiene en cuenta la incertidumbre del modelo, y la incertidumbre debida a la variabilidad en futuras observaciones. 5.7. Procesos puntuales. La teoría de procesos puntuales tiene bastante utilidad en el campo de los valores extremos (en particular, tienen especial utilidad en el campo de la ingeniería), pues proporciona herramientas útiles que sirven para demostrar resultados importantes para valores extremos. Un proceso puntual se puede definir, de forma no demasiado formal, como una distribución aleatoria de puntos dentro de un espacio. Una vez que se ha definido un proceso puntual, se pueden calcular probabilidades como las siguientes: -Probabilidad de ocurrencia de un número dado de sucesos. -Probabilidad del tiempo que pasa entre sucesos consecutivos. -Probabilidad de que el suceso k-ésimo ocurra en un tiempo sea mayor que un cierto valor t. Según Coles, existen dos motivos por los que considerar esta aproximación: el primero, porque proporciona una interpretación del comportamiento de los valores extremos que unifica todos los modelos vistos hasta ahora; segundo, el modelo conduce directamente a una verosimilitud que permite una formulación más natural de la no-estacionariedad en las superaciones de umbrales de la que se obtiene con el modelo de Pareto generalizado. 94 5.8. Caso de colas pesadas. En Estadística, las distribuciones con colas pesadas son aquellas cuyas colas son más pesadas que la de la distribución exponencial, que es la distribución referencia para afirmar si una distribución tiene colas pesadas o no. Según Embrechts, Klüppelberg y Mikosch (2008), este tipo de distribuciones son importantes sobre todo en series financieras. Al tener las colas más pesadas, hay más probabilidad concentradas en ellas, luego es más probable encontrar valores extremos en ese tipo de distribuciones que en una distribución que no tenga colas pesadas. 95 Bibliografía. [1] Agarwal, P. (2008). Structural Reliability of Offshore Wind Turbines. ProQuest. ISBN: 9780549738763. [2] Aguirre Jaime, A. (1994). Introducción al Tratamiento de Series Temporales: Aplicación a las Ciencias de la Salud . Ediciones Díaz de Santos . ISBN: 978-8479781538. [3] Albeverio S., Jentsch V. y Kantz, H. (2005). Extreme Events in Nature and Society. Springer. ISBN: 978-3540286103. [4] Beirlant J., Goegebeur Y., Teugels J. y Segers J. (2004). Statistics of Extremes. Theory and Applications. Wiley. ISBN: 978-0471976479. *5+ Bowerman B.L., O’Connell R.T. (2007). Pronósticos, Series de Tiempo y Regresión: Un Enfoque Aplicado (Cuarta Edición). ISBN: 978-9706866066. [6] Castillo , E., Hadi, A. S. Balakrishnan, N. y Sarabia, J. M. (2004). Extreme Value and Related Models with Applications in Engineering and Science. Wiley. ISBN: 978-0471671725. [7] Coles , S. (2001). An Introduction to Statistical Modeling of Extreme Values. Springer. ISBN: 978-1852334598. [8] David, H. A., Nagaraja, H.N. (2003). Order Statistics. Wiley. ISBN: 978-0471389262. [9] de Haan L. y Ferreira A. (2006). Extreme Value Theory. An Introduction. Springer. ISBN: 9780387239460. [10] Embrechts, P., Klüppelberg, C., Mikosch, T. (1997). Modelling Extremal Events for Insurance and Finance. Springer. ISBN: 978-3540609315. [11] Galambos, J. (1978). The Asymptotic Theory of Extreme Order Statistics. Wiley. ISBN 9780471021483. 96 [12] Goda Y., Kioka W. y Nadaoka K. (2004). Asian and Pacific Coasts 2003: Proceedings of the 2nd international Conference. World Scientific Publishing Co Pte Ltd; Pap/Cdr edition. ISBN: 978-9812385581. [13] Gumbel E. J. (2004). Statistics of Extremes. Courier Dover Publications. ISBN: 9780486436043. [14] Ketchen, D.J., Ketchen, D. J. Jr., Bergh, D. D. (2006). Research Methodology in Strategy and Management, Volume 3. Emerald Group Publishing Limited. ISBN: 978-0762313396 [15] Kotz, S. y Nadarajah, S. (2001). Extreme Value Distributions. Theory and Applications. World Scientific. ISBN: 978-1860942242. [16] Kropp, J. (2010). In Extremis: Disruptive Events and Trends in Climate and Hydrology. Springer. ISBN: 978-3642148620. [17] Leadbetter, M. R., Lindgren, G. y Rootzén, H. (1983). Extremes and Related Properties of Random Sequences and Processes. First Edition. Springer. ISBN: 978-0387907314. [18] Reiss, R-D. , Thomas, M. (2007). Statistical Analysis of Extreme Values With Applications to Insurance, Finance, Hidrology and Other Fields. Third Edition. Birkhauser Verlag. ISBN: 9783764372309 [19] Resnick, S. I. (2007). Extreme Values Regular Variation and Point Processes. Theory. Springer. ISBN: 978-0387759524. [20] Shumway R. H., Stoffer D. S. (2006). Time Series Analysis and Its Applications. With R Examples. Springer. ISBN: 978-0387293172. [21] Tsay, R.S. (2005). Analysis of Financial Time Series. Wiley. ISBN: 978-0471690740. 97 [22] Wooldridge, J. M. (2010). Introducción a la Econometría: un Enfoque Moderno (Spanish Edition). (2010). Paraninfo. ISBN: 978-8428380188. 98