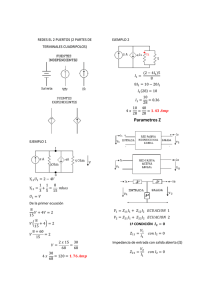
impedancia
Anuncio

CIRCUITOS DE CA EN SERIE Y EN PARALELO Mg. Amancio R. Rojas Flores LA LEY DE OHM PARA CIRCUITOS DE CA Resistores El voltaje senoidal Puede ser escrito en forma de faso como siendo Dado que la resistencia del vector puede ser expresado como Podemos evaluar la corriente fasorial como sigue : Mg. ARRF 2 Fig.1 voltaje Sinusoidal y corriente por un resistor Si queremos convertir a fasor la corriente de su forma sinusoidal Nuevamente la relación entre la magnitud del fasor y el valor pico sinusoidal equivalente es dado por Mg. ARRF 3 Ejemplo 1 Referente a el resistor mostrado en la Figura a.Hallar la corriente sinusoidal usando fasores b. Bosqueje la forma sinusoidal par a para v y i. c. Bosqueje el diagrama fasorial de V y I. Solución a) c) b) Mg. ARRF 4 Ejemplo 2 Referente al resistor de la Figure a. Use el algebra fasorial para encontrar el voltage sinusoidal , v. b. Bosqueje la forma de onda sinusoidal para v y i. c. Bosqueje el diagrama fasorial que muestre V y I. Solución a) c) b) Mg. ARRF 5 Inductores Ejemplo 3 Si conocemos la reactancia de un inductor , ela ley de ohm la corriente en el inductor puede ser expresado en fasor como: Considere el inductor mostrado en la figura a. Determine la expresión sinusoidal para la corriente i usando fasores. b. Bosqueje la forma de onda sinusoidal para v y i. c. Bosqueje el diagrama fasorial mostrando V y I. Solución a) b) c) Mg. ARRF 6 Capacitores La corriente en el capacitor expresado en forma fasorial es: Ejemplo 4 Considere el capacitor mostrado en la figura a. Encuentre el voltaje v a través del capacitor. b. Bosqueje la forma de onda senoidal para v y i. c. Bosqueje el diagrama fasorial mostrando V y I. Solución a) b) Mg. ARRF 7 CIRCUITO DE CORRIENTE ALTERNA EN SERIE Las propiedades generales de los circuitos de CA en serie , son las mismas que las de los circuitos de cd; o sea. Cuando trabajamos co circuitos CA no solo trabajamos con resistencia sino tambien con reactancia capacitiva y inductiva. Impedancia es un termino usado determinar colectivamente la como la resistencia, capacitancia y inductancia “impiden” la corriente en un circuito . El símbolo para impedancia es la letra Z y su unidad es el ohm (Ω). Por lo tanto la impedancia puede estar compuesto por la combinación de resistencias y reactancias y es escrito como una cantidad vectorial Z, donde: Mg. ARRF 8 Matemáticamente cada vector impedancia puede ser escrito como sigue: Todo vector impedancia puede aparecer en el primer o cuarto cuadrante , pero el vector impedancia siempre es positivo Para un circuito AC en serie de n impedancias como muestra la figura Mg. ARRF 9 Considere la figura Podemos determinar la impedancia del circuito De la figura podemos ver la impedancia total de los elementos en serie consiste de un componente rela y uno imaginario . La correspondiente impedancia rtotal puede ser escrito en forma polar o rectangular La forma rectangular es escrito como La forma polar es escrito como Mg. ARRF 10 Ejemplo. Considere la red de la figura a. hallar ZT. b. Bosqueje el diagrama de impedancia para la red y indique si la impedancia total del circuito es inductiva, capacitiva o resistiva. c. Use la ley de ohm para determinar I, VR , y Vc. Solución a. La impedancia total es el vector suma b. El correspondiente diagrama de impedancia es mostrado en la figura c) Mg. ARRF 11 Ejemplo. Determine la impedancia Z que podría estar dentro del block indicado en la figura Solución Convirtiendo la impedancia total de su forma polar a rectangular Mg. ARRF 12 LA LEY DE VOLTAGE DE KIRCHHOFF y LA REGLA DEL DIVISOR DE VOLTAGE Cuando un voltaje es aplicado a las impedancias en serie , como se muestra en la figura ,la ley de ohm puede ser usado para determinar el voltaje a través de alguna impedancia La corriente en el circuito es Ahora, por sustitución arribamos a la regla del divisor de voltaje para una alguna combinación en serie de elementos como: Mg. ARRF 13 Ejemplo. Considere el circuito de la figura. a. Hallar ZT. b. Determine el voltaje VR y VL usando la regla del divisor de voltaje c. Verifique la ley de voltaje de Kirchhoff en la malla. Solución a) b) c) La ley de voltaje de Kirchhoff en la malla dara Mg. ARRF 14 Ejemplo. Considere el circuito de la Figura a. Calcular el voltaje sinusoidal v1 y v2 usando fasores y la regla del divisor de voltaje. b. Bosqueje el diagrama fasorial mostrando E, V1, y V2. c. Sketch the sinusoidal waveforms of e, v1, and v2. Solución a. El fasor de la fuente de voltaje es determinado como Aplicando la regla del divisor de voltaje Los voltaje sinusoidal serán determinados como Mg. ARRF 15 b. El diagrama fasorial se muestra en la figura c. El correspondiente voltaje senoidal es mostrado Mg. ARRF 16 CIRCUITO DE C.A EN PARALELO La admitancia Y de alguna impedancia es definido como una cantidad vectorial la cual es el reciproco de la impedancia Z. Donde la unidad de admitancia es el siemens (S). En particular , tenemos que notar que la admitancia de un resistor R es llamado conductancia y esta dado por el simbolo YR. Si determinamos la admitancia de un componente reactivo puro X , la admitancia resultante es llamada Suceptancia de el componente y es asignado por el simbolo B. la unidad para la suceptancia es Siemens (S) Mg. ARRF 17 De manera similar que la impedancia, la admitancia puede ser representado en el plano complejo en un diagrama de admitancia, como se muestra en la figura. Fig. diagrama de Admitancia mostrando conductancia (YR) y susceptancia (YL y YC). Mg. ARRF 18 Ejemplo. Determine la admitancia de las siguientes impedancias. Bosqueje la correspondiente diagrama de admitancia . b. XL= 20Ω. XC= 40 Ω a. R=10 Ω Solución Fig. Diagrama de admitancia Mg. ARRF 19 Para redes de n admitancias como se muestra en la figura ,el total de admitancia es el vector suma de las admitancias de la red. La impedancia resultante de la red en paralelo de n impedancias es determinado como: Mg. ARRF 20 Ejemplo. Encontrar la admitancia equivalente y la impedancia de la red de la figura Solución Mg. ARRF 21 Dos impedancias en paralelo Tres impedancias en paralelo Mg. ARRF 22 LA LEY DE CORRIENTE DE KIRCHHOFF y LA REGLA DEL DIVISOR DE CORRIENTE Mg. ARRF 23 Ejemplo. Calcular la corriente en cada rama de la red de la figura Solución Mg. ARRF 24 Ejemplo. En referencia al circuito de la figura a. Hallar la impedancia total , ZT. b. Determine la fuente de corriente , IT. c. Calcule I1, I2, y I3 usando la regla del divisor de corriente. d. Verifique la ley de corrientes en el nodo a. Solución a) Las reactancias inductiva y capacitiva estan en paralelo y tienen el mismo valor, podemos remplazarlos por un circuito abierto en consecuencia solo el resistor puede ser considerado b) c) d) Mg. ARRF 25