Coordenadas rectangulares y polares

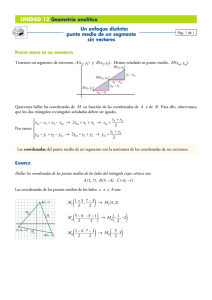
UNIDAD 1.
Coordenadas rectangulares y polares
Juan Adolfo Álvarez Martínez
Autor
1
GEOMETRIA ANALÍTICA
La Geometría Analítica es un área de la matemática en la que el álgebra y la
geometría están relacionadas entre sí. Esto hace posible resolver
algebraicamente (analíticamente) problemas geométricos. Y En forma recíproca
también nos permite resolver geométricamente problemas algebraicos.
Los Objetivos básicos al estudiar geometría analítica son en general:
a).-Dada una
corresponde.
expresión
algebraica,
determinar
la
gráfica
que
le
b).- Dada una gráfica en el plano de coordenadas, encontrar la expresión
algebraica correspondiente.
CONCEPTOS BÁSICOS.
Plano Cartesiano.
En geometría analítica es un requisito indispensable usar un plano cartesiano
el cual considera dos ejes, perpendiculares entre sí: OX y OY, que se cortan
en su origen. Determinando un plano.
Este plano que se forma de los dos ejes constituye lo que se conoce como
plano cartesiano.
Al eje X se le denomina eje de las abscisas, al eje Y , eje de las
ordenadas y al punto O , de intersección de ambas rectas, origen.
A cada punto P del plano le corresponde un sólo par ordenado de números
reales, llamados coordenadas de P.
La representación geométrica o gráfica de dicho par ordenado de este
punto cualquiera P es:
2
Se puede ver que el primer número significa la cantidad de unidades en el eje
“x” y el segundo indica el número de unidades en “y”
Hay que aclarar que el número de unidades en cualquier eje puede ser positivo
o negativo: Por ejemplo un punto M cuyas coordenadas sean (3,-5) significa
que hay que recorrer 3 unidades en “x” , es decir hacia la derecha del origen y
5 unidades hacia abajo a partir de este mismo origen.
La siguiente figura nos muestra las características de un plano
cartesiano.
EJERCICIO 1. Localización de puntos.
El plano cartesiano se divide en cuatro cuadrantes como ya pudiste darte
cuenta.
Dependiendo de las coordenadas de un punto, éste se localiza en un
determinado cuadrante.
Ahora, emplea una hoja en papel milimétrico en la cual vas a trazar un plano
cartesiano para localizar y colocar ubicar y poner una marca para cada uno de
los siguientes puntos:
Pto A (-5, 3)
Pto B (3,2)
Pto C (-1,-4)
Pto D (0,5)
Pto E (3,0)
Pto F (8,3)
Pto G (5,8)
3
Ya que tengas localizados los puntos completa la información de la tabla
siguiente, donde se solicita indiques el cuadrante en que se ubican los puntos
del A hasta el G.
Punto y sus coordenadas: P (x,y)
Cuadrante donde se
localiza:
A
B
C
D
E
F
G
A continuación traza semirrectas de colores de la siguiente manera:
SEGMENTO NUMERO:
1 con rojo
2 con rojo
3 con rojo
4 con azul
5 con azul
6 con azul
6 con azul
Usando los PUNTOS
AyB
ByC
CyA
DyE
EyF
FyG
GyD
DISTANCIA ENTRE DOS PUNTOS.
Una primera iniciación al conocimiento del plano cartesiano en esta asignatura
es la aplicación al concepto de distancia entre dos puntos. Esto es; dados dos
puntos del plano:
Un punto p1 de coordenadas (x1,y1) y un punto P2 de coordenadas (x2,y2) la
distancia entre ellos viene dada por la fórmula:
Y es igual a La distancia entre los puntos 1-2.
4
Lo que Gráficamente tenemos como:
Puedes observar que en la formula aparece una raíz cuadrada y unas
diferencias elevadas al cuadrado, lo que significa que esto tiene que ver con el
teorema de Pitágoras, ya que es el cálculo de una hipotenusa que se obtiene a
partir de la raíz cuadrada
da de la suma de los cuadrados de los lados como ya
sabes.
Aunque lo correcto en matemáticas es saber y demostrar las formulas, no es
nuestra intención profundizar mucho en ello, pero sí es importante mencionarlo
para conocer el origen de la formula de la
l distancia.
Ejemplo 1:
Calcula la distancia entre los puntos A ( 2 , – 3 ) y B ( 5 , 1 ) del plano.
primer
imer punto y cuál es el segundo.
Primero iniciamos definiendo cual es el pr
En este caso el punto A (2,
(2,-3)
3) será el punto 1 cuyas coordenadas
corresponden a (x1,y1).
Luego el punto B ( 5 , 1 ) será el punto 2 de coordenadas (x2,y2)
5
Ahora se procede a sustituir en la formula los valores de las coordenadas.
Esto es:
y tenemos:
d =
( 5 – 2 ) 2 + (1 + 3 ) 2
Se puede ver que en el segundo paréntesis la resta se convierte en suma por
las leyes de los signos. Y continuando con el procedimiento, elevando cada
termino al cuadrado:
Y gráficamente se representa como:
Ejemplo 2.
Determine la distancia que hay entre los puntos F (-2, -4) y K (-3, 8)
Procedemos de igual forma que en el caso anterior:
6
Ejemplo de aplicación.
Demostrar que las diagonales del rectángulo cuyos vértices son los puntos a (1,2),
B (4,7), c (-6,13) y D (-9,8) son iguales.
Primero trazamos el rectángulo en el plano cartesiano:
x,y
a( 1, 2)
B (4, 7)
c(-6,13)
D (-9, 8)
Como podemos observar, lo que debemos hacer es calcular la distancia entre los
puntos
(a y c) que es la primer diagonal y la distancia entre (D y B) que es la otra
diagonal.
Nuestro proceso para los puntos a-c es:
Ahora la diagonal 2:
Si comparamos los resultados obtenidos de las dos distancias, vemos que en
efecto
da-c = d B-D
…… l.q.q.d.
7
(Que significa lo que queríamos demostrar)
Ejercicio 2
a) Los puntos U(1,1), V(5,3) y W(6,-4) son vértices de un polígono. Con esta
información y aplicando la formula de distancia indique qué tipo de triangulo
forman dichos puntos y sus características de dicho triangulo.
b) Demostrar que los puntos (-2,-1), (2,2) y (5, -2) son los vértices de un triangulo
isósceles y calcule además su área.
Comprueba tu solución analítica dibujando en papel milimétrico con plano
cartesiano el polígono. Mide con una regla o escuadra todos los lados y obtén el
perímetro.
Coordenadas del punto medio de un segmento de recta.
Sean A ( x 1 , y 1 ) y B ( x 2 , y 2 ) , 2 puntos cualesquiera del plano los
cuales forman un segmento de recta. Si se desea dividir en dos partes iguales
este segmento tenemos que las coordenadas del punto medio se obtienen
mediante:
x = x1 + x2
2
,
y = y1 + y2
2
Ejemplo 1:
Dados los puntos A (8 , 6 ) y
punto medio de la distancia AB .
B ( – 4 , 12 ) , determina las coordenadas del
El procedimiento consiste en aplicar las formulas, y consideramos al punto A
(x1,y1) como el primer punto y a B (x2,y2) como el segundo punto, luego vamos a
definir a M como el punto medio del trazo AB , entonces sus coordenadas son:
x = x1 + x2 = 8+ (-4) = 4 = 2 ,
2
2
2
y = y1 + y2 = 6 + 12 = 18 = 9
2
2
2
8
Por lo que las coordenadas del punto medio : M son ( 2 , 9 )
lo cual podemos verificar en la siguiente grafica.
Ejemplo 2:
Calcule las coordenadas del punto medio del segmento de recta cuyos extremos
son los puntos
(-2,-3) y (4,2) y diga el cuadrante en el que se encuentra este
punto medio.
Vamos a aplicar las fórmulas conocidas:
x = x1 + x2 = -2+4 = 2 = 1 , y = y1 + y2 = -3 +2 = -1
2
2
2
2
2
Entonces las coordenadas del punto medio son M
encuentra en el 40 cuadrante.
1, -1
2
y el punto se
2
Ejercicios para practica.
aa). Uno de los extremos de un segmento de recta es el punto (1,-3) y el
punto medio es ( 0, 2). Hallar las coordenadas (x,y) del otro extremo del
segmento de recta.
Sugerencia: en este caso hay que despejar x2 y y2 de cada formula.
bb). Calcula las coordenadas de los puntos medios de cada lado del triangulo
cuyos vértices son: (5, -2), (-2,-1) y (2,2).
Comprueba con un plano cartesiano y dibujo del polígono en hoja milimétrica.
9
Hemos visto hasta el momento dos temas: como obtener la distancia entre 2
puntos y como calcular las coordenadas de un punto medio entre dos puntos.
Ahora bien, dado un segmento de recta con el que podemos unir dos puntos, no
únicamente se puede dividir éste en 2 partes iguales para encontrar su punto
medio sino que podemos dividir dicho segmento en “N” partes diferentes y
encontrar las coordenadas del punto en que se ha dividido.
Esto es lo que se conoce como:
División de un segmento en una razón dada
Sean A ( x 1 , y 1 ) y B ( x 2 , y 2 ) , puntos cualesquiera del plano y R un
punto del trazo AB , tal que AR = r
donde “r” es la razón que divide al
segmento en dos partes AB:
Entonces las coordenadas de R son:
x = x1 +r(x2-x1)
y = y1 + r(y2-y1)
Ejemplo 1:
Dados los puntos A ( – 7 , 5 ) y B ( 8 , 15 ) , determina las coordenadas del
punto R del trazo AB , que divide al segmento de recta en la razón 2/3es decir tal
que:
el segmento AR se ubique a los 2/3 de AB, lo que matemáticamente escribimos
como:
Para resolver el ejercicio, vemos que la razón en que ha de dividirse el segmento
es 2/3, lo que significa que las coordenadas a calcular se obtienen mediante los
datos:
10
Ejercicio para practicar.
Determine las coordenadas del punto R tal que el segmento de recta formado por
D(3,4) y B (1,12) se divida en la razón 1/3
EJEMPLOS A LA VIDA COTIDIANA.
Para este momento ya te habrás preguntado en que se aplican estos
conceptos de coordenadas, distancia entre puntos y puntos medios.
11
La respuesta la tienes en el archivo UNIDAD 1 que contiene la presentación de
power point de los temas vistos.
Vamos a continuar entonces con una aplicación del tema visto.
La situación es la siguiente:
Imagina que vas a ir de viaje a un safari en áfrica central y para que te
asegures de no perderte te das a la tarea de investigar los datos sobre
distancias, aeropuertos y características dónde vas a ir de turista.
Entonces lo primero que se hay que hacer es aplicar lo que se ha visto hasta el
momento, luego un mapa va a ser nuestro recurso para aplicar los
conocimientos.
El mapa que se va a usar es el de la siguiente imagen, el cual ya está a escala
y es confiable para nuestros propósitos.
-
Entonces la primer actividad es identificar la escala a la que esta
dibujado.
-
Después tenemos que trazar un plano cartesiano lo cual realizaremos
como se muestra en el segundo grafico. Considera para esta situación
12
que el origen está en un punto donde la empresa que organiza los
Tours, tiene sus oficinas centrales.
-
Hecho esto, vemos que cada unidad de cuadricula representa en la
realidad 200 kilómetros de distancia, entonces si se viaja en avión,
podemos calcular cuántos kilómetros hay entre cualquier par de puntos
siempre que conozcamos las coordenadas de éstos.
-
Explicado lo anterior usamos el mapa para hacer algunos cálculos
aplicando las formulas conocidas entre los puntos que ya se han
definido en la tabla que esta a continuación y anotamos los resultados.
Solo hay que recordar que las coordenadas están en kilómetros.
-
Vamos pues a poner en práctica los conocimientos.
En la siguiente página se muestra el mapa y los datos de las
localidades.
13
localidad
Oficinas centrales
Walikale (Punto A)
Kigali (Punto B)
Bujumbura (punto C)
coordenadas
0,0
-200,-150
0,-200
-50,-350
La actividad a realizar es contestar los siguientes incisos.
Calcula cuantos kilómetros hay entre:
a) Kigali y Bujumbura
b) Walikale y Bujumbura
c) ¿Cual localidad está más cerca de las oficinas centrales, y a cuantos
kilómetros está?
Elabora una tabla donde estén indicadas las distancias, las cuales deben estar
fundamentadas en sus respectivos procedimientos.
14