Discusión sobre la potencia reactiva y la

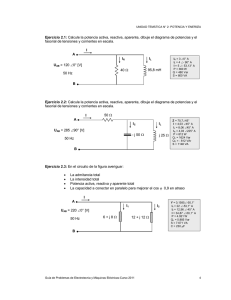
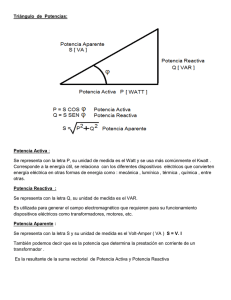
Asociación Española
para el Desarrollo de la
Ingeniería Eléctrica
Universidad de Sevilla
XVII REUNIÓN DE GRUPOS DE INVESTIGACIÓN
DE INGENIERÍA ELÉCTRICA
Sevilla, marzo de 2007
DISCUSIÓN SOBRE LA POTENCIA REACTIVA Y LA
POTENCIA APARENTE EN SISTEMAS CON
DESEQUILIBRIOS Y DISTORSIÓN
J. R. VÁZQUEZ, P. SALMERÓN, R. S. HERRERA Y S. P. LITRÁN
Departamento de Ingeniería Eléctrica y Térmica
Universidad de Huelva
RESUMEN
Para asegurar la continuidad y calidad en el suministro eléctrico, además de
unas adecuadas instalaciones, es necesario conocer de forma precisa los
flujos de potencia eléctrica que circulan por las redes, ya que afectan, entre
otros aspectos, al diseño de los equipos de medida, a la definición de tarifas
eléctricas, o a una correcta elección de las técnicas de compensación a
emplear. En sistemas sinusoidales y monofásicos (o trifásicos equilibrados),
conceptos como la potencia útil o activa, la potencia reactiva, la potencia
aparente o el factor de potencia son bien conocidos y tienen definiciones
aceptadas universalmente. Sin embargo, en sistemas distorsionados o
desequilibrados, el análisis del flujo de potencias se hace más complejo, no
existiendo unas definiciones únicas para algunos de esos términos.
El trabajo desarrollado realiza una introducción al análisis del flujo de
potencias en redes desequilibradas y con distorsión, haciendo especial
hincapié en la limitada validez de algunas de las definiciones clásicas de
potencias usadas en sistemas sinusoidales y equilibrados, cuando se aplican a
estos sistemas. Así, se tomará como referencia el Standard IEEE 100-1988,
justificando a lo largo del trabajo la necesidad de introducir uno nuevo: el
Standard IEEE 1459-2000. Para ilustrar la afirmación anterior, por un lado
se presentan los resultados de simulación de distintos casos prácticos,
desarrollados en el entorno Matlab-Simulink, y por otro se realizan
mediciones reales sobre una plataforma experimental. Los resultados
obtenidos confirman la necesidad de adoptar una formulación común para los
términos de potencia en sistemas distorsionados y con desequilibrio. El
análisis de los términos de potencia incluidos en el Standard IEEE 1459-2000
se presenta en un segundo artículo de la presente reunión.
1. Introducción
El estudio del flujo de la potencia eléctrica en sistemas eléctricos sinusoidales y
monofásicos (o trifásicos equilibrados) es hoy día bien conocido. En estos sistemas, conceptos
como la potencia útil o activa, las potencias reactiva y aparente, o el factor de potencia como
medida del rendimiento eléctrico de la instalación, son conocidos y aceptados por todos, [1,2].
Sin embargo, la aparición de cargas no lineales, en especial las cargas electrónicas de
potencia, que por un lado han permitido desarrollar nuevas e interesantes aplicaciones (control
de iluminación, variación de velocidad de motores, conversión avanzada de potencia, etc.),
por otro lado han provocado alteraciones de la calidad del sistema eléctrico, además de
complicar el análisis del flujo de potencias que tiene lugar en esos sistemas. Las intensidades
que consumen las cargas, y como consecuencia de su circulación por el sistema, las tensiones
que alimentan las cargas no son ya sinusoidales, es decir, están distorsionadas, siendo
necesario para su estudio su formulación a través de las correspondientes componentes
armónicas. En la figura 1 se muestra un esquema de la situación planteada.
i(t)
+
Deformación de la
onda de tensión
Sala de PCs
...
-
Figura 1. Esquema de un sistema eléctrico con cargas no lineales
El desarrollo en serie de Fourier permite expresar la intensidad, i(t), como suma de
armónicos, o sea, de señales sinusoidales de frecuencia múltiple de la fundamental, ecuación
(1). El armónico de orden n tiene un valor eficaz In, un ángulo ϕn, y una frecuencia nω,
siendo ω la frecuencia fundamental de la señal en cuestión. Las ecuaciones (2) y (3) muestran
las expresiones del valor eficaz de la señal, I, y de un índice que indica el grado de distorsión
de la señal, el factor de distorsión total, THD, referido en este caso a la componente
fundamental de la señal, I1. Idéntico desarrollo se tendría para la tensión, v(t).
i (t ) = ∑ 2 I n cos(nωt − ϕ n )
n =1
2
I = I 12 + I 22
THD1 =
+ ... +
∑I
n=2
I N2
2
n
I1
(1)
(2)
(3)
Además de los efectos no deseados que implican los armónicos al circular por el sistema
(pérdida de rendimiento eléctrico de la instalación, sobrecalentamiento de equipos,
vibraciones y pérdidas de potencia en motores, salto intempestivo de protecciones eléctricas,
etc.), obligan a una redefinición, no cerrada aún hoy día, de los distintos términos de potencia.
Una muestra de la complejidad e importancia que ha ido cobrando en las dos últimas
décadas el estudio de la calidad de la potencia eléctrica, y en particular lo referente a los
armónicos, son los trabajos de organizaciones internacionales como CENELEC, IEC, CIGRE
e IEEE, que mantienen comités dedicados al desarrollo de normativas en ese campo.
El presente trabajo pretende realizar una introducción al análisis del flujo de potencias en
redes desequilibradas y con distorsión, haciendo especial hincapié en la limitada validez de
algunas de las definiciones clásicas de potencias usadas en sistemas sinusoidales y
equilibrados, según el Standard IEEE 100-1988, [3], cuando se aplican a estos sistemas.
Para ilustrar las afirmaciones realizadas a lo largo del trabajo, en el sentido indicado, se
incluyen los resultados de simulación de distintos casos prácticos, realizados en el entorno
Matlab-Simulink. Concluye el trabajo con la realización de un montaje de laboratorio, una
carga trifásica distorsionada y desequilibrada, en la que se han medido los flujos de potencia
mediante un equipo analizador de la calidad de la potencia eléctrica. Los resultados obtenidos
permitirán contrastar las afirmaciones formuladas a lo largo del trabajo.
2. Flujo de potencias en sistemas monofásicos
En las definiciones incluidas en este trabajo, se ha adoptado la notación del diccionario de
la organización IEEE (Institution of Electrical and Electronic Engineering). Así, la potencia
aparente, U, se define como el producto de los valores eficaces de la tensión, E, y la tensión, I.
Se trata de una cantidad que no tiene definida una dirección de flujo.
U = EI
(4)
El factor de potencia, FP, se define como la relación entre la potencia media o activa, P,
y la potencia aparente.
P
FP =
(5)
U
Si tensión e intensidad son sinusoidales, la potencia aparente es numéricamente igual a la
potencia activa máxima, y el factor de potencia es igual al coseno del ángulo que la tensión
adelanta a la intensidad.
FP = cosθ
(6)
En sistemas sinusoidales, las pérdidas se determinan por el producto de los valores
eficaces de tensión e intensidad, por lo que la potencia aparente es la utilizada, por ejemplo,
en la caracterización de generadores, transformadores o cables. Sin embargo, en sistemas no
sinusoidales, el producto indicado no es suficiente para considerar las pérdidas que aparecen.
En un transformador, por ejemplo, las pérdidas por histéresis son proporcionales a la
frecuencia, mientras que las de vacío son proporcionales al cuadrado de la frecuencia. La
circulación de armónicos implica unas pérdidas adicionales, que llevan a una disminución de
la capacidad efectiva de transformación en un factor K.
El concepto de potencia reactiva es muy usado en circuitos lineales alimentados por
tensiones sinusoidales. Esta potencia reactiva, Q, se define como la amplitud de la oscilación
de la potencia instantánea, y no transfiere energía neta. Está causada por la energía
almacenada en las bobinas y condensadores del sistema, y aunque no contribuye a la
transferencia neta de energía, implica la circulación de intensidades por los distintos equipos,
que hay que considerar para su correcto dimensionado.
Q = E I cosθ
(7)
Se adopta el criterio de que los condensadores generan potencia reactiva y las bobinas la
consumen, representando la potencia reactiva la energía media intercambiada entre estos
elementos almacenadores de energía.
Con señales no sinusoidales, Q se define en el diccionario IEEE como la suma de las
potencias reactivas de cada uno de las componentes armónicas, según la descomposición de
Budeanu, [4]. Dado que las potencias reactivas de cada armónico pueden presentar distintos
signos, contribuirán en igual o en sentido contrario a la potencia reactiva total.
Q = ∑ E n I n senθ
n
(8)
Es importante destacar que seguir una u otra formulación para el flujo de potencias, en
concreto para la potencia reactiva y/o la potencia aparente, tiene consecuencias en aspectos
tales como la elección de los métodos de medida y compensación, la existencia de
incongruencias en la lectura de la potencia reactiva de una instalación, o la determinación del
factor de potencia, con claras implicaciones legislativas y económicas, [5,6].
Para ilustrar las afirmaciones realizadas a lo largo del trabajo, en el sentido anteriormente
indicado, se incluyen los resultados de simulación de distintos casos prácticos, realizados en
el entorno Matlab-Simulink. Concluye el trabajo con la realización de un montaje de
laboratorio, una carga trifásica distorsionada y desequilibrada, en la que se han medido los
flujos de potencia mediante un equipo analizador de la calidad de la potencia eléctrica. Los
resultados obtenidos permitirán contrastar las afirmaciones formuladas a lo largo del trabajo.
En el caso práctico 1, se muestra que en cargas sin elementos almacenadores de energía,
como el regulador ac/ac de la figura 2, la potencia reactiva resulta distinta de cero.
i= 2
∑I
n =1, 2 ,3...
n
sen(nωt + θ )
+
e = 2 E senθ
-
Figura 2. Regulador ac/ac
A partir de la ecuación (8), y dado que la tensión sólo incluye el armónico de orden 1 o
fundamental, la potencia reactiva consumida por la carga es:
Q = ∑ E n I n senθ = E I 1 senθ1
n
(9)
Para calcular la potencia reactiva, se ha realizado la simulación del circuito en el
entorno Matlab-Simulink, considerando una frecuencia de 50 Hz, una tensión de alimentación
E=100 V, y una resistencia R=10 Ω. En la figura 3 se muestran las formas de onda de tensión
e intensidad para un ángulo de disparo de 60º.
200
100
a)
0
-100
-200
0
0.01
0.02
0.03
0.04
0.05
0.06
0
0.01
0.02
0.03
0.04
0.05
0.06
0
0.01
0.02
0.03
0.04
0.05
0.06
20
10
b)
0
-10
-20
2500
2000
c)
1500
1000
500
0
-500
Figura 3. Formas de onda en un regulador monofásico, con un ángulo de disparo de 60º; a)
tensión de alimentación, b) intensidad consumida, c) potencia instantánea.
Como se observa en la figura 3c, en ningún momento se tiene una potencia instantánea
negativa, es decir, la dirección de la potencia es siempre de fuente a carga. Sin embargo, la
potencia reactiva resulta Q = 234,6 VAr. En definitiva, para valores de α≠0, la potencia
reactiva es distinta de cero, aún sin existir elementos almacenadores de energía. Para explicar
esto, en la figura 4 se presentan los espectros de tensión e intensidad, y en la figura 5 los
correspondientes armónicos fundamentales.
Figura 4. Espectros armónicos de tensión e intensidad en un regulador monofásico
20
ϕ V-ϕ I = 16,34º
10
0
150
-10
0.009
100
0.0095
0.01
0.0105
0.011
0.0115
50
0
-50
-100
-150
0
0.01
0.02
0.03
0.04
0.05
0.06
Figura 5. Tensión de un regulador monofásico y componente fundamental de la intensidad
Como se observa en la figura 5, el armónico fundamental de la intensidad está retrasado
respecto a la tensión de alimentación, lo que implica una potencia reactiva positiva. Para otros
ángulos de disparo se tiene una situación idéntica.
En el caso práctico 2, un circuito RLC alimentado por una tensión distorsionada, figura 6,
se muestra que puede haber intercambio energético entre fuente y carga, es decir, un factor de
potencia menor que la unidad, y ser nula la potencia reactiva calculada.
i
+
e = 100 2 sen(ωt )
L=0,825 mH C=11,97 mF
R=10Ω
+10 2 sen(3ωt )
-
Figura 6. Carga lineal RLC
Con la tensión de alimentación y los valores de R, L y C señalados en la figura, las
formas de onda resultantes se muestran en la figura 7.
100
a)
0
-100
0
0.01
0.02
0.03
0.04
0.05
0.06
0.01
0.02
0.03
0.04
0.05
0.06
0.01
0.02
0.03
0.04
0.05
0.06
200
100
b)
0
-100
-200
0
4
x 10
2
1
c)
0
-1
-2
0
Figura 7. Formas de onda en circuito RLC alimentado con tensión no sinusoidal;
a) tensión de alimentación, b) intensidad del circuito, c) potencia instantánea.
En la figura 8 se muestra el espectro armónico de las señales de tensión e intensidad. Al
tratarse de una carga lineal, la intensidad sólo incluye los armónicos presentes en la tensión,
es decir, los de orden 1 y 3.
% del arm. fundamental
% del arm. fundamental
100
100
Fundamental (50Hz) = 141.4
THD= 0.00%
80
60
60
40
40
20
20
0
0
5
10
15
20
Fundamental (50Hz) = 11.76
THD= 36 80%
80
25
Orden del armónico
0
0
5
10
15
20
25
Orden del armónico
Figura 8. Espectros armónicos de tensión e intensidad.
Las componentes de orden 1 y 3 de la intensidad están retrasadas y adelantadas,
respectivamente, de las componentes de orden 1 y 3 de la tensión, por lo que la potencia
reactiva a la frecuencia fundamental es positiva y a la frecuencia triple es negativa. Así, las
potencias activa y reactiva resultan:
P1 = 1000 W
P 3 = 10W
Q1 = 1000 VAr
Q3 = −1000 VAr
(10)
Según (10), las potencias reactivas transportadas por los armónicos de orden 1 y 3 se
cancelan. En definitiva, se tiene:
P = 1010W
Q = 0 VAr
FP = 0.1
(11)
Este resultado permite constatar que la potencia reactiva definida en (8) no tiene el
mismo significado físico que en sistemas sinusoidales, ya que resulta nula en un caso en el
que existe un intercambio energético entre fuente y carga (la potencia instantánea presenta
valores negativos). Para elevar el factor de potencia hasta la unidad, se puede realizar la
compensación de la potencia reactiva de cada armónico.
Se considera ahora la definición de potencia de distorsión, D, del diccionario IEEE. Es
una cantidad escalar, en cuadratura con las potencias activa y reactiva, y se calcula a partir de
la potencia aparente, U, según la ecuación 13.
2

 

 ∑ Pn  + ∑ Qn 
 n
  n

S=
D=
2
(12)
(U )2 −(S )2
(13)
La descomposición de la potencia aparente, U, en potencia activa, P, reactiva, D, y de
distorsión, D, fue introducida por Budeanu. La potencia de distorsión puede ser cero incluso
aunque tensión e intensidad no tengan igual forma o fase (ver caso 1), y no tiene porqué ser
cero cuando tensión e intensidad tienen idéntica forma y fase (ver caso 2). No existe una regla
aceptada para su signo. Realmente, esta potencia no refleja ningún fenómeno físico o
energético concreto, y sólo se introduce cuando se constata que el cuadrado de la potencia
reactiva, Q2, es menor que la diferencia U2-P2.
3. Definiciones de los términos de potencia en circuitos polifásicos
En circuitos trifásicos, se extienden las definiciones anteriormente expuestas de los
flujos de potencias. Así, siguen sin un sentido físico la potencia aparente, reactiva, y de
distorsión en circuitos trifásicos no sinusoidales. Además, aparecen más ambigüedades
cuando se describen circuitos incluso lineales, en el caso de que existan desequilibrios.
En el diccionario de IEEE, existen dos tipos de potencia aparente para circuitos
trifásicos, la potencia aparente aritmética, Ua, y potencia aparente “vector”, U. En las
ecuaciones 18 y 19 se muestran sus expresiones. El índice x representa cada una de las fases.
U a = ∑U x = ∑ E x I x = ∑
x
x
2
2
(14)
x
2
U=
2
Px + Q x + D x
2

 
 

 ∑ Px  + ∑ Q x  +  ∑ D x 
 x
  x
  x

2
(15)
La potencia aparente U, dada por la ecuación (19), coincide con el módulo del vector
de potencia U. Si la descomposición de la potencia aparente en sus componentes ortogonales
P, Q y D es igual para todas las fases, ambas definiciones coinciden. Si no, la potencia
aritmética Ua es mayor que U.
En circuitos trifásicos, se extienden las definiciones de los flujos de potencias. Así, sigue
sin un sentido físico la potencia reactiva en sistemas distorsionados, y aparecen más
ambigüedades cuando se describen circuitos desequilibrios. En el caso práctico 3, se muestra
cómo en una carga reactiva desequilibrada, figura 9, la potencia aparente U puede ser nula. El
caso práctico 4, figura 10, ilustra que en sistemas desequilibrados, términos como la potencia
aparente o el factor de potencia, dependen de la forma de medida de las tensiones, respecto a
qué punto neutro.
FUENTE
i1
Ea
e1
e2
e3
S
MEDIDA
S
+Z
+
Eam
S
i2
EbS + Z
XL j
i3
+
Ebm
S
EcS + Z
XC j
+ m
Ec
Zm
Figura 9. Carga desequilibrada.
CARGA
Zm
+ l
Va
+
Vbl
+l
Vc
Zal
Zbl
Zcl
Zm
Figura 10. Circuito equilibrado con neutro aislado
En el circuito de la figura 9, un sistema de tensiones equilibradas de secuencia directa
alimenta dos reactancias que cumplen XL = XC. Las intensidades resultan equilibradas, aunque
de secuencia inversa, existiendo pérdidas en la transmisión de potencia de fuente a carga. Las
potencias trifásicas activa, reactiva y de distorsión, así como la potencia aparente U, resultan
cero. Tras la simulación del circuito, con E=100 V y ZC=ZL=1 Ω, los valores de la potencia
activa y reactiva de cada fase son:
P3 = 17320W
Q2 = −15000 W Q3 = 0VAr
P1 = −8660 W
P2 = −8660 W
Q1 = 15000 VAr
(16)
(17)
En efecto, la suma de las potencias de las tres fases resulta nula, aunque existe una
circulación de corriente de fuente a carga.
El circuito de la figura 10 muestra otra ambigüedad de los sistemas desequilibrados, la
dependencia de la forma de medida. Para el análisis de esta situación, hay que considerar que
existen dos posibles factores de potencia, Fpa ó Fp, según se considere, respectivamente, la
potencia aparente aritmética o la de tipo vector. Cuando las tensiones son sinusoidales y
equilibradas, el factor de potencia de tipo vector no varía si se consideran las tensiones de
fuente, Es, del punto de medida, Em, o de la carga, El, es decir, Fps=Fpm= Fpl. Sin embargo, se
tienen dos valores distintos del factor de potencia aritmético, uno si se usan tensiones de
fuente o de medida, y otro si se usan las tensiones de la carga, Fps=Fpm≠ Fpl. El motivo es la
existencia de una tensión entre los distintos puntos neutros. Las diferencias aumentan si las
tensiones no son sinusoidales. Para contrastar esta afirmación, se ha simulado el circuito con
los parámetros indicados en las ecuaciones 18 y 19. Los resultados, en cuanto a valores del
factor de potencia, se indican en la ecuación 20.
ea = E (sin(ωt ) + 0,05 sin(3ωt ))
Z = 10 Ω
l
a
F =F
S
p
m
p
= F =1
l
p
E = 100 V
Z = −10 j Ω
l
b
F
S
p ,a
=F
m
p ,a
R S = 1 mΩ
R m = 1 kΩ
Z = 10 j Ω
l
c
= 0,356
F
l
p ,a
= 0,118
(18)
(19)
(20)
Resultados similares se tienen con un desequilibrio en las tensiones de alimentación. En
definitiva, hay que tener precaución al usar el factor de potencia de un circuito trifásico
desequilibrado, especialmente si se considera el de tipo aritmético.
4. Desarrollo de un montaje experimental
Para contrastar de forma experimental los resultados indicados en el trabajo, se ha
desarrollado en el laboratorio el montaje de una carga trifásica distorsionada y desequilibrada,
un regulador trifásico con ramas resistivas, figura 11. Se registraron las lecturas de tensión e
intensidad con un equipo analizador de red trifásico, marca Circutor AR5. En la tabla I se
muestran los resultados obtenidos. El analizador calcula la potencia reactiva y el factor de
potencia por fase, según las expresiones manejadas en el presente trabajo, ecuaciones (8) y (5)
respectivamente. Las potencias trifásicas (indicadas con el subíndice III) son la suma de las
tres monofásicas, mientras que el factor de potencia trifásico es el cociente PIII/SIII, es decir, el
factor de potencia aritmético. Los valores de la mitad inferior de la tabla han sido calculados a
partir de las lecturas del equipo.
L1
L2
L3
N
Regulador
trifásico
desequilibrado
36º
50 Ω
72º
50 Ω
108º 50 Ω
K
a)
c)
b)
d)
Figura 11. Montaje de laboratorio; a) esquema de conexión, b) parámetros del regulador
trifásico ensayado, c) foto del ensayo con analizador conectado, d) detalle de la carga
Tabla I. Flujos de potencia en un regulador trifásico conectado en estrella,
con punto medio conectado al neutro de la instalación
Términos de potencia
E1, E2, E3 (V)
I1, I2, I3 (A)
P1, P2, P3 (W)
Lecturas
Q1, Q2, Q3 (VAr)
registradas
Fp1, Fp2, Fp3
PIII (W)
QIII (VAr)
Fp,III=Fpa
S1, S2, S3 (VA)
U1, U2, U3 (VA)
D1, D2, D3 (VAd)
P1/S1, P2/S2 P3/S3
P (W)
Valores
Q (VAr)
calculados
D (VAd)
Uvector (VA)
Ua (VA)
Fp
Fpa
Lecturas del equipo Circutor AR5
218,7
223
224,1
3,910
3,425
2,145
833,9
656,4
272,0
152,6
293,4
289,4
0,9700
0,8509
0,5601
1762,4
735,4
0,84
847,7
719,0
397,2
855,3
763,9
480,7
113,7
258,1
270,8
0,98
0,91
0,69
1762,4
735,4
642,6
2014,8
2100,0
0,87
0,84
Como se observa en la tabla, los resultados experimentales confirman los obtenidos en
simulación. Una carga distorsionada, aún sin presencia de elementos almacenadores de
energía, presenta una potencia reactiva distinta de cero. Otro hecho a destacar es la diferencia
entre el factor de potencia real (Fp=P/U) y el que se mediría, por ejemplo, en una instalación
con contadores de energía activa y reactiva analógicos (P/S), con las correspondientes
implicaciones económicas. Si se repite el ensayo con el interruptor K abierto, las diferencias
son mayores. Así, el factor de potencia resulta 0,82 al medir con las tensiones de
alimentación, y 0,77 con las tensiones reales de la carga.
5. Conclusiones
Para realizar una introducción al estudio del flujo de potencia en sistemas distorsionados
y desequilibrados, se ha partido de las definiciones del estándar IEEE 100-1988.
Los ejemplos monofásicos presentados permiten concluir que una red distorsionada, sin
elementos almacenadores de energía, puede presentar una potencia reactiva distinta de cero.
Además, en una red lineal, alimentada con tensiones distorsionada, puede haber circulación
de intensidad reactiva de distintas frecuencias, aunque la potencia reactiva total puede resultar
nula, por lo que esta cantidad no resulta de interés para la compensación del sistema, que sí
podría realizarse frecuencia a frecuencia. Los ejemplos trifásicos permiten concluir que cargas
desequilibradas pueden presentar una potencia reactiva total nula, aunque exista una
intensidad reactiva circulando entre la fuente y la carga, y que algunos de los términos de
potencia dependen del punto de medida. En particular, se mostró que la potencia aparente
aritmética (y el factor de potencia obtenido a partir de ella) era una cantidad muy variable, y
por tanto no era una buena referencia. Las conclusiones anteriores se contrastaron de forma
experimental con las mediciones realizadas en el laboratorio sobre un regulador trifásico.
Las paradojas presentadas en los distintos casos prácticos, muestran la necesidad de
revisar las definiciones de los términos de potencia, tal y como aparecían en el diccionario de
IEEE de 1988. En esta línea se ha desarrollado el Standard IEEE 1459-2000, que aunque
avanza en esta dirección, aún no cierra la discusión de los términos de potencia en sistemas
distorsionados y/o desequilibrados.
6. Referencias
[1] IEEE Tutorial Course, “Power System Harmonics”. Ed. IEEE Power Engineering
Society, 1984.
[2] A. E. Emanuel, “Harmonics in the Early Years of Electrical Engineering: a Brief Review
of Events, People and Documents”. Proceedings of 9th International Conference on
Harmonics and Quality of Power, October 2000, Vol. 1, pp. 1-7.
[3] “ANSI/IEEE Standard 100-1988, IEEE Standard Dictionary of Electrical and
Electronics Terms” (Fourth Edition). The Institute of Electrical and Electronics
Engineers, Inc., New York, NY, 1988.
[4] C. I. Budeanu, “Reactive and Fictive Powers”. Nacional Romanian Institute, Bucarest,
Romania, 1927.
[5]
P. S. Filipski, “Polyphase Apparent Power and Power Factor under Distorted
Waveforms Conditions”. IEEE Transactions on Power Delivery, Vol. 6, No. 3, July
1991.
[6]
L. S. Czarnecki, T. Swietlicki, “Power in Non-Sinusoidal Networks: their
Interpretation, Analysis and Measurement”. IEEE Trans. on Instrumentation and
Measurement, IM-39, 1990, no. 2, pp. 340-345.